- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Финансовая математика. Случайное событие. Случайная величина презентация
Содержание
- 2. 1. Случайное событие 2. Случайная величина Глава 4. Финансовая математика
- 3. Случайное событие Вопрос 4.1.90 Под
- 5. Случайное событие Вероятность события А :
- 6. Случайное событие Вопрос
- 7. Случайное событие Р(А) = 6/30 =
- 8. Случайное событие Теорема сложения вероятностей: Вероятность суммы
- 9. Случайное событие Вопрос 4.2.137 Даны следующие вероятности
- 10. Случайное событие Р(АВС) = Р(А)*Р(В)*Р(С) =
- 11. Случайное событие Сочетаниями называют комбинации, составленные
- 12. Случайное событие Вопроса: 4.2.125
- 13. Случайное событие С mn =
- 14. Случайная величина Случайная величина
- 15. Случайная величина 2 формы закона распределения : функция распределения плотность распределения
- 16. Случайная величина В форме функции
- 17. Случайная величина В форме плотности
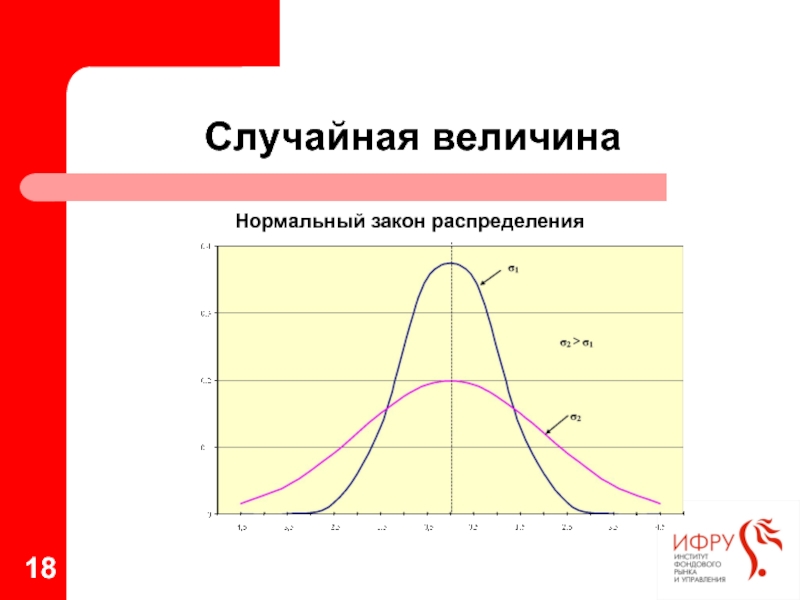
- 18. Случайная величина Нормальный закон распределения
- 19. Случайная величина
- 20. Случайная величина Вероятность попадания случайной величины в
- 21. Случайная величина Вопрос 4.2.107 Пусть Х -
- 22. Случайная величина P ≈ 68,3%
- 23. Случайная величина Вопрос 4.2.120 Доходность акции А
- 24. Случайная величина P ≈ {0;60}
- 25. Случайная величина Числовые характеристики M
- 26. Случайная величина Вопрос 4.2.126 Через год
- 27. Случайная величина M [X] =
- 28. Случайная величина Вопрос 4.2.129 Доходность актива за
- 29. Случайная величина σX = √ D [X]
- 30. Случайная величина Свойства числовых характеристик M
- 31. Случайная величина Вопрос 4.1.96
- 32. Случайная величина М(Х+2) = М(Х)
- 33. Случайная величина Вопрос 4.2.104 Пусть Х -
- 34. Случайная величина Вопрос 4.2.105 Пусть
- 35. Случайная величина D(2Х + 1)= D(2Х)
- 36. Случайная величина Вопрос 4.2.140 Даны
- 37. Случайная величина M [9X-6Y+80] = M
- 38. Случайная величина Дисперсия суммы двух случайных величин
- 39. Случайная величина Kxy = M [(X
- 40. Случайная величина Вопрос 4.2.103 Пусть Х и
- 41. Случайная величина D [X+Y] = D
- 42. Случайная величина Вопрос 4.2.123 Ковариация
- 43. Случайная величина rxy = Kxy
- 44. Случайная величина Вопрос 4.2.132 Стандартное
- 45. Случайная величина
- 46. Случайная величина Вопроса: 4.2.128 Прогноз инвестора относительно
- 47. Случайная величина E портфеля = Σ Θi
Слайд 3Случайное событие
Вопрос 4.1.90
Под случайным событием в теории вероятности понимается некоторый
факт, который характеризуется следующими признаками:
I. Наблюдается однократно;
II. Может наблюдаться неоднократно;
III. Нельзя с полной определенностью утверждать - произойдет он в очередной раз или нет;
IV. При условии контроля условий эксперимента можно утверждать с полной определенностью, произойдет он или нет.
Ответы:
A. I и IV
B. II и III
C. II, III или IV
D. III
I. Наблюдается однократно;
II. Может наблюдаться неоднократно;
III. Нельзя с полной определенностью утверждать - произойдет он в очередной раз или нет;
IV. При условии контроля условий эксперимента можно утверждать с полной определенностью, произойдет он или нет.
Ответы:
A. I и IV
B. II и III
C. II, III или IV
D. III
Слайд 4
Случайное событие
Достоверное событие – это событие, которое происходит всегда.
Невозможное событие – это событие, которое в силу объективных причин в результате опыта произойти не может.
Слайд 5Случайное событие
Вероятность события А :
P (A) = m/n
где
n – общее
число возможных случаев;
m – число случаев, благоприятных событию А.
Р(А) = 1, если случайное событие – достоверное
Р(А) = 0, если случайное событие - невозможное
m – число случаев, благоприятных событию А.
Р(А) = 1, если случайное событие – достоверное
Р(А) = 0, если случайное событие - невозможное
Слайд 6Случайное событие
Вопрос 4.2.111
Документы профессионального участника пронумерованы от 1 до 30. Какова
вероятность того, что случайно будет открыт документ с номером, кратным 5?
Слайд 8Случайное событие
Теорема сложения вероятностей:
Вероятность суммы двух совместимых событий равна:
Р(А+В) =
Р(А)+Р(В)-P(A*B)
Теорема умножения вероятностей:
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную при условии, что первое событие имело место:
P(A*B) = Р(А)*Р(В/А)
Если события независимы, то:
P(A*B) = Р(А)*Р(В)
Теорема умножения вероятностей:
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную при условии, что первое событие имело место:
P(A*B) = Р(А)*Р(В/А)
Если события независимы, то:
P(A*B) = Р(А)*Р(В)
Слайд 9Случайное событие
Вопрос 4.2.137
Даны следующие вероятности роста доходности акций компаний «А», «В»
и «С»: Р(А)=0,8; Р(В)=0,7; Р(С)=0,9.
Какова вероятность того, что доходности акций трех компаний вырастут?
Какова вероятность того, что доходности акций трех компаний вырастут?
Слайд 10Случайное событие
Р(АВС) = Р(А)*Р(В)*Р(С) = 0,8*0,7*0,9 = 0,504
Ответы:
А. 0,504
В. 0,994
С. 0,974
D.
0,404
Слайд 11Случайное событие
Сочетаниями называют комбинации,
составленные из n различных элементов по m
элементов, которые отличаются хотя бы одним элементом.
Число сочетаний:
С mn = n! / (m! (n - m)!)
Число сочетаний:
С mn = n! / (m! (n - m)!)
Слайд 12Случайное событие
Вопроса: 4.2.125
Имеется 10 разных акций. Инвестор хотел бы построить портфель
из трех акций, включив каждую из них по одной штуке. Сколько вариантов портфелей может сформировать инвестор?
Слайд 14Случайная величина
Случайная величина – величина, которая в результате опыта может
принять то или иное значение, неизвестно заранее, какое именно.
Слайд 15Случайная величина
2 формы закона распределения :
функция распределения
плотность распределения
Слайд 16Случайная величина
В форме функции распределения F(x)
закон распределения имеет следующий
вид:
F(X) = P(X
F(X) = P(X
Слайд 17Случайная величина
В форме плотности распределения
закон распределения имеет следующий вид:
f
(x) = F’ (X)
Слайд 20Случайная величина
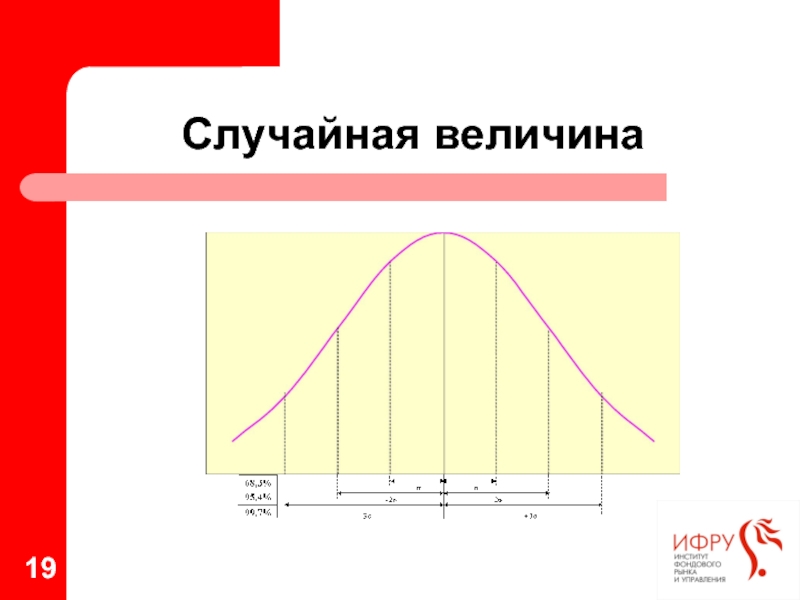
Вероятность попадания случайной величины в симметричный относительно математического ожидания диапазон,
ширина которого кратна значению стандартного отклонения:
P ≈ 68,3% → ± 1*σ
P ≈ 95,4% → ± 2*σ
P ≈ 99,7% → ± 3*σ
σX = √ D [X]
P ≈ 68,3% → ± 1*σ
P ≈ 95,4% → ± 2*σ
P ≈ 99,7% → ± 3*σ
σX = √ D [X]
Слайд 21Случайная величина
Вопрос 4.2.107
Пусть Х - случайная величина, распределенная по нормальному закону,
М - математическое ожидание, D - дисперсия случайной величины, М(Х)=2, D(X)=0,25. Укажите верное утверждение из следующих:
I. Х принимает значения с вероятностью 68,3% в интервале от 1,75 до 2,25;
II. Х принимает значения с вероятностью 68,3% в интервале от 1,5 до 2,5;
III. Х принимает только положительные значения.
I. Х принимает значения с вероятностью 68,3% в интервале от 1,75 до 2,25;
II. Х принимает значения с вероятностью 68,3% в интервале от 1,5 до 2,5;
III. Х принимает только положительные значения.
Слайд 22Случайная величина
P ≈ 68,3% → 2 ± 1*σ → {1,5;2,5};
P
≈ 95,4% → 2 ± 2*σ → {1,0;3,0};
P ≈ 99,7% → 2 ± 3*σ → {0,5;3,5};
Ответы:
A. Только I и III
B. Только II и III
C. Только I
D. Только II
P ≈ 99,7% → 2 ± 3*σ → {0,5;3,5};
Ответы:
A. Только I и III
B. Только II и III
C. Только I
D. Только II
Слайд 23Случайная величина
Вопрос 4.2.120
Доходность акции А распределена нормально. Среднее значение доходности равно
30% годовых, стандартное отклонение доходности в расчете на год равно 15%. Определить, с какой вероятностью через год доходность акции может оказаться в диапазоне от нуля до 60%.
Слайд 25Случайная величина
Числовые характеристики
M [X] = Σ xi * pi
D [X]
= M [ (X - M (X))2 ]
σX = √ D [X]
σX = √ D [X]
Слайд 26Случайная величина
Вопрос 4.2.126
Через год цена акции может иметь следующее распределение:
Цена акции
30 руб. 40 руб. 50 руб.
Вероятность 30% 60% 10%
Определить математическое ожидание цены акции через год.
Вероятность 30% 60% 10%
Определить математическое ожидание цены акции через год.
Слайд 27Случайная величина
M [X] = Σ xi * pi = 30*0,3 +
40*0,6 + 50*0,1 = 38 руб.
Ответы:
A. 38 руб.
B. 40 руб.
C. 60 руб.
Ответы:
A. 38 руб.
B. 40 руб.
C. 60 руб.
Слайд 28Случайная величина
Вопрос 4.2.129
Доходность актива за 3 года представлена в таблице:
Определить риск
актива, представленный показателями выборочной дисперсии и стандартного отклонение доходности.
Слайд 29Случайная величина
σX = √ D [X]
М(Х) = (10+14+18)/3 = 14
D
[X] = M [ (X - M (X))2] = [(10 – 14)2 + (14 – 14) 2 + (18 – 14) 2 ]/3
= 10,67
σX = √ D [X] = 3,27%
Ответы:
A. 10,67; 3,27% B. 32; 5,66% C. 89,5; 9,47% D. 108; 10,39%
= 10,67
σX = √ D [X] = 3,27%
Ответы:
A. 10,67; 3,27% B. 32; 5,66% C. 89,5; 9,47% D. 108; 10,39%
Слайд 30Случайная величина
Свойства числовых характеристик
M [с] = с
D [с] = 0
M [X+с] = M [X] +с D [X+с] = D [X]
M [с*X] = с*M [X] D [с*X] = с2* D [X]
M [X+с] = M [X] +с D [X+с] = D [X]
M [с*X] = с*M [X] D [с*X] = с2* D [X]
Слайд 31Случайная величина
Вопрос 4.1.96
Пусть Х - случайная величина, М - математическое ожидание,
М(Х)=0,5. Найти М(Х +2).
Слайд 32Случайная величина
М(Х+2) = М(Х) + М(2) = 0,5 + 2 =
2,5
Ответы:
A. 2,5
B. 4,5
C. 5
D. Указанных данных недостаточно для решения задачи
Ответы:
A. 2,5
B. 4,5
C. 5
D. Указанных данных недостаточно для решения задачи
Слайд 33Случайная величина
Вопрос 4.2.104
Пусть Х - случайная величина, М - математическое ожидание,
D - дисперсия случайной величины, М(Х)=0,5, D(X)=2,25.
Найти D(Х + 2).
Ответы:
A. 1,5
B. 2,25
C. 2,5
D. Указанных данных недостаточно для решения задачи
Найти D(Х + 2).
Ответы:
A. 1,5
B. 2,25
C. 2,5
D. Указанных данных недостаточно для решения задачи
Слайд 34Случайная величина
Вопрос 4.2.105
Пусть Х - случайная величина, М - математическое ожидание,
D - дисперсия случайной величины, М(Х)=0,5, D(X)=1,5. Найти D(2Х + 1).
Слайд 35Случайная величина
D(2Х + 1)= D(2Х) = 22*D(Х)= 4*1,5 = 6
Ответы:
A. 1,5
B.
4
C. 6
D. Указанных данных недостаточно для решения задачи
C. 6
D. Указанных данных недостаточно для решения задачи
Слайд 36Случайная величина
Вопрос 4.2.140
Даны 3 актива. Известно, что ожидаемая доходность первого актива
X = 30%, ожидаемая доходность второго актива Y = 20%. Определить ожидаемую доходность актива Z, если известно, что Z=9X-6Y+80.
Слайд 37Случайная величина
M [9X-6Y+80] = M [9X] - M [6Y] + M
[80] = 9*30 – 6*20 + 80 = 230
Ответы:
А. 230
В. 150
C. 1710
D. 3150
Ответы:
А. 230
В. 150
C. 1710
D. 3150
Слайд 38Случайная величина
Дисперсия суммы
двух случайных величин
D [X+Y] = D
[X] + D [Y] + 2*Kxy
D(Х + Y) = D(Х) + D(Y), если Х и Y – независимые случайные величины
D(Х + Y) = D(Х) + D(Y), если Х и Y – независимые случайные величины
Слайд 40Случайная величина
Вопрос 4.2.103
Пусть Х и Y - случайные величины, D -
дисперсия случайной величины, К - ковариация, D(Х)=0,5, D(Y)=1,5, К(Х,Y)= -0,5. Найти D(Х + Y).
Слайд 41Случайная величина
D [X+Y] = D [X] + D [Y]+2* Kxy =
0,5 + 1,5 + 2*(-0,5)= 1
Ответы:
A. 1,5
B. 2
C. 1
Ответы:
A. 1,5
B. 2
C. 1
Слайд 42Случайная величина
Вопрос 4.2.123
Ковариация доходностей акций А и В равна 120. Стандартное
отклонение доходности акций А и В равно 20% и 30%. Определить коэффициент корреляции доходностей акций.
Слайд 44Случайная величина
Вопрос 4.2.132
Стандартное отклонение доходности первого актива равно 25%, второго –
34%, коэффициент корреляции между доходностями активов 0,65. Определить ковариацию доходностей активов.
Слайд 45Случайная величина
r xy = Kxy / σX * σY
Kxy = r xy * σX * σY = 0,65*25*34 = 552,5
Ответы:
A. 552,5
B. 0,765
C. 7,65
Kxy = r xy * σX * σY = 0,65*25*34 = 552,5
Ответы:
A. 552,5
B. 0,765
C. 7,65
Слайд 46Случайная величина
Вопроса: 4.2.128
Прогноз инвестора относительно возможных сценариев доходности акций компаний А
и В с учетом их вероятностей в следующем периоде представлен в таблице:
Определить ожидаемую доходность портфеля, если уд. веса акций А и В в портфеле составляют соответственно 30% и 70%.
Определить ожидаемую доходность портфеля, если уд. веса акций А и В в портфеле составляют соответственно 30% и 70%.
Слайд 47Случайная величина
E портфеля = Σ Θi * Mi
M [X] =
Σ xi * pi
M1 = 10*0,5 + 40*0,5 = 25
M2 = 10*0,6 + 20*0,4 = 14
E портфеля = 0,3*25 + 0,7*14 = 17,3%
A. 17,3%
B. 20%
C. 25%
M1 = 10*0,5 + 40*0,5 = 25
M2 = 10*0,6 + 20*0,4 = 14
E портфеля = 0,3*25 + 0,7*14 = 17,3%
A. 17,3%
B. 20%
C. 25%






















![Случайная величина Числовые характеристики M [X] = Σ xi * pi D [X] = M [ (X](/img/tmb/5/496860/31a3b867c02b6dd31c2539814fc6b30d-800x.jpg)

![Случайная величинаM [X] = Σ xi * pi = 30*0,3 + 40*0,6 + 50*0,1 = 38](/img/tmb/5/496860/8f6192d5835f68ccdb8e25cf44bd4f54-800x.jpg)

![Случайная величинаσX = √ D [X] М(Х) = (10+14+18)/3 = 14D [X] = M [](/img/tmb/5/496860/9bec03b0989d7d74c26c670fadf3e972-800x.jpg)
![Случайная величина Свойства числовых характеристикM [с] = с D](/img/tmb/5/496860/fc99587e5e95dde722ffdbd49f370c3c-800x.jpg)






![Случайная величинаM [9X-6Y+80] = M [9X] - M [6Y] + M [80] = 9*30 –](/img/tmb/5/496860/c71e71c71fa89c0699441d33ca87c974-800x.jpg)
![Случайная величина Дисперсия суммы двух случайных величин D [X+Y] = D [X] + D [Y] +](/img/tmb/5/496860/4bb2c0e19c904ee62575d1006feec32b-800x.jpg)
![Случайная величина Kxy = M [(X – Mx)(Y – My)] rxy = Kxy / σX *](/img/tmb/5/496860/e0edea8310bbb4a0cc1f2aa1bfd34200-800x.jpg)

![Случайная величинаD [X+Y] = D [X] + D [Y]+2* Kxy = 0,5 + 1,5 +](/img/tmb/5/496860/9f64f427d14ccf9831c8e92a690413de-800x.jpg)





![Случайная величинаE портфеля = Σ Θi * Mi M [X] = Σ xi * piM1](/img/tmb/5/496860/a9f32929b9e25aef8505a13e78fb69f8-800x.jpg)





