- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории оболочек вращения презентация
Содержание
- 1. Основы теории оболочек вращения
- 2. Основы теории оболочек вращения безмоментная теория оболочек;
- 3. Геометрия оболочек вращения Срединной или средней поверхностью
- 4. Геометрия оболочек вращения Геометрия оболочки вращения полностью
- 5. Геометрия оболочек вращения Срединная поверхность оболочки вращения
- 6. Геометрия оболочек вращения Произвольную точку срединной поверхности
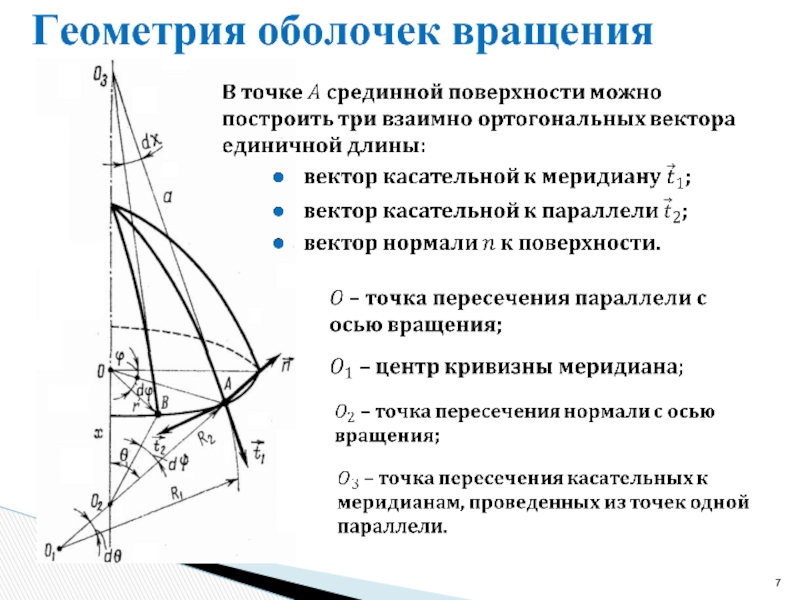
- 7. Геометрия оболочек вращения
- 8. Геометрия оболочек вращения
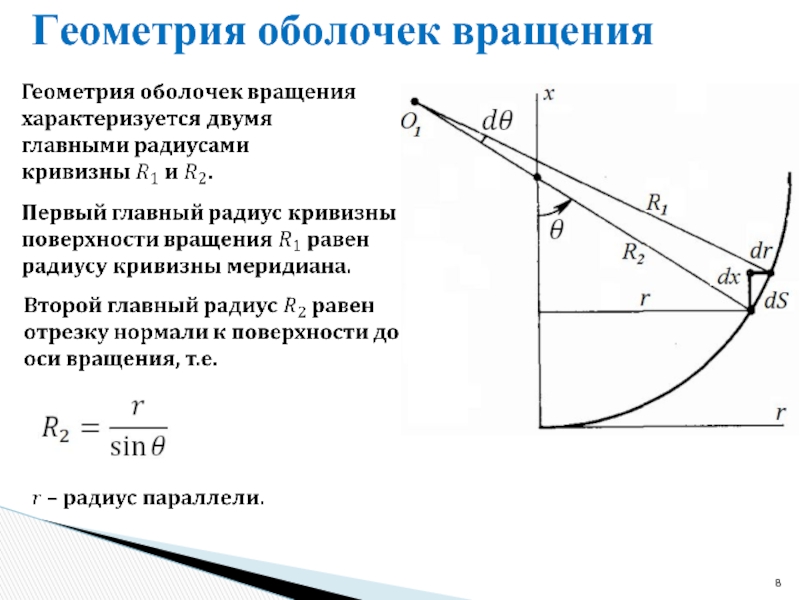
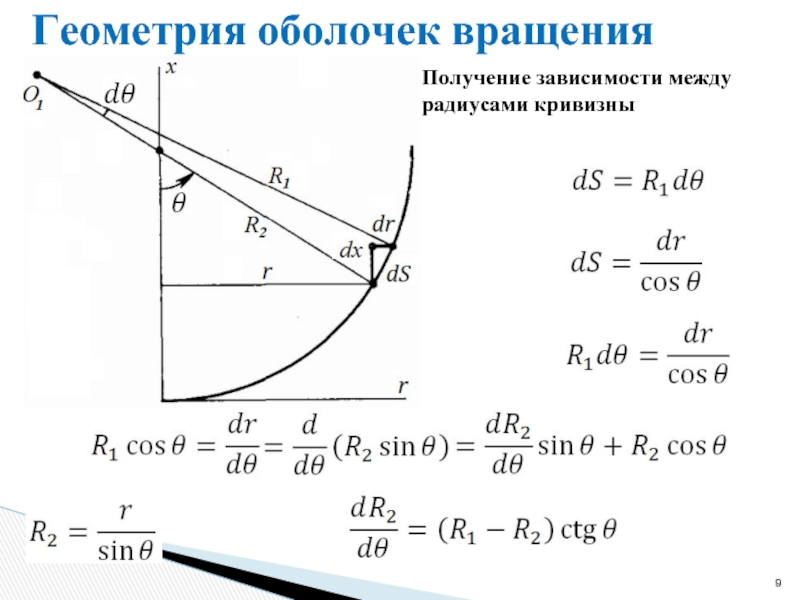
- 9. Геометрия оболочек вращения Получение зависимости между радиусами кривизны
- 10. Гипотезы Кирхгофа остается прямолинейным, нормальным к деформированной
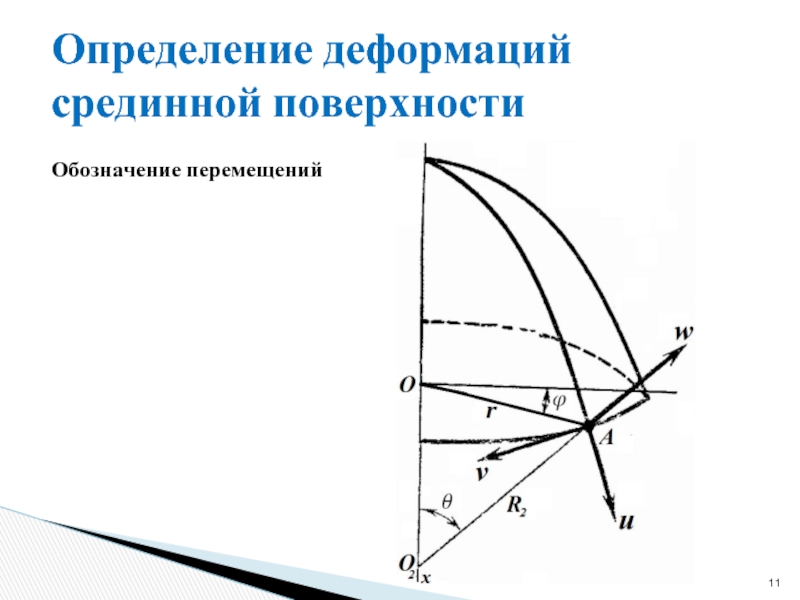
- 11. Определение деформаций срединной поверхности Обозначение перемещений
- 12. Определение деформаций срединной поверхности Деформация срединной поверхности в плоскости меридиана
- 13. Определение деформаций срединной поверхности Деформация срединной поверхности в направлении параллели
- 14. Определение деформаций срединной поверхности Деформация сдвига элемента срединной поверхности оболочки
- 15. Определение деформаций срединной поверхности
- 16. Определение деформаций срединной поверхности Цилиндрическая оболочка
- 17. Определение деформаций срединной поверхности Сферическая оболочка
- 18. Безмоментная теория оболочек Согласно этой теории считают,
- 19. Безмоментная теория оболочек В безмоментной теории
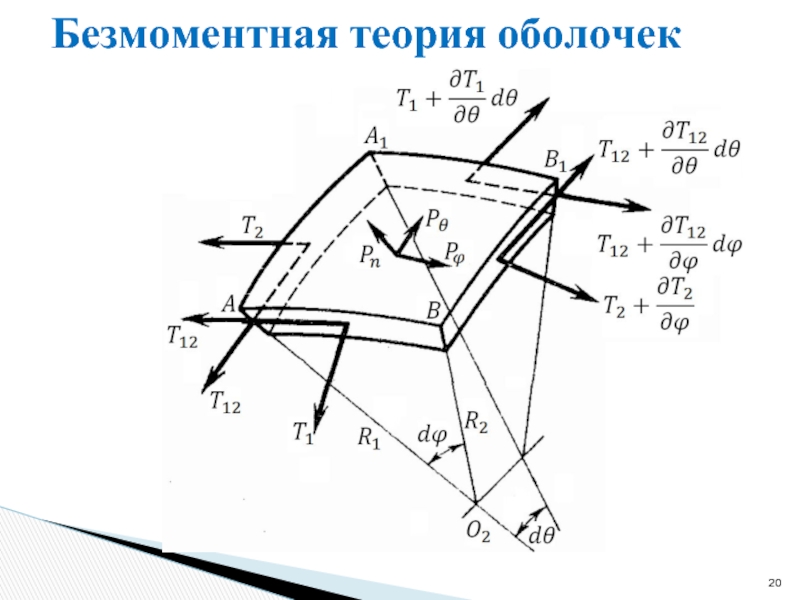
- 20. Безмоментная теория оболочек
- 21. Безмоментная теория оболочек Уравнения равновесия – уравнение Лапласа
- 22. Безмоментная теория оболочек Физические соотношения Геометрические соотношения
- 23. Уравнения безмоментной теории оболочек для осесимметричной задачи Уравнения равновесия
- 24. Уравнения безмоментной теории оболочек для осесимметричной задачи Физические соотношения Геометрические соотношения
- 25. Сферическая оболочка при действии внутреннего давления Для
- 26. Цилиндрическая оболочка при действии внутреннего давления Для
- 27. Цилиндрическая оболочка при действии внутреннего давления Осевая деформации Перемещение Погонные усилия Окружная деформация
- 28. Цилиндрическая и сферическая оболочка при действии внутреннего
- 29. Особенности работы оболочек
- 30. Уравнения моментной теории оболочек
- 31. Уравнения моментной теории оболочек
- 32. Уравнения моментной теории оболочек Выражения для деформаций
- 33. Уравнения моментной теории оболочек Выражения для деформаций
- 34. Уравнения моментной теории оболочек Физические соотношения (слой оболочки считают находящимся в условиях ПНС):
- 35. Уравнения моментной теории оболочек меридиональное погонное
- 36. Уравнения моментной теории оболочек Погонные моменты: погонный
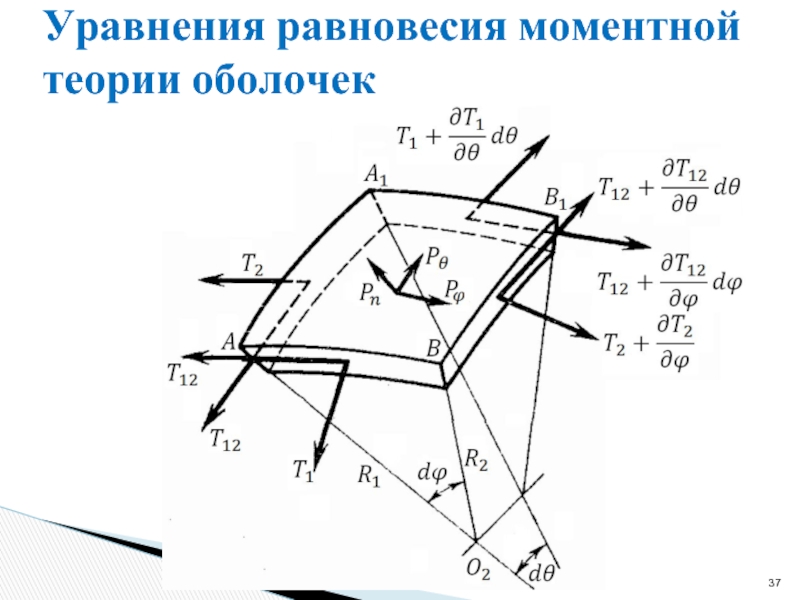
- 37. Уравнения равновесия моментной теории оболочек
- 38. Уравнения равновесия моментной теории оболочек
- 39. Уравнения равновесия моментной теории оболочек На рисунке
- 40. Уравнения равновесия моментной теории оболочек Уравнение равновесия
- 41. Полная система уравнений моментной теории оболочек Геометрические соотношения:
- 42. Полная система уравнений моментной теории оболочек Физические соотношения:
- 43. Полная система уравнений моментной теории оболочек Уравнения равновесия:
- 44. Уравнения моментной теории оболочек при осесимметричной деформации Геометрические соотношения:
- 45. Физические соотношения Уравнения моментной теории оболочек при осесимметричной деформации
- 46. Уравнения равновесия Уравнения моментной теории оболочек при осесимметричной деформации
- 47. Краевой эффект для цилиндрической оболочки Для цилиндрической оболочки
- 48. Краевой эффект для цилиндрической оболочки Из
- 49. Краевой эффект для цилиндрической оболочки
- 50. Краевой эффект для цилиндрической оболочки
- 51. Благодарю за внимание!
Слайд 2Основы теории оболочек вращения
безмоментная теория оболочек;
моментная теория оболочек.
Оболочка является более сложным
Оболочку называют тонкой, если ее толщина значительно меньше (в 20 и более раз), чем прочие размеры.
Слайд 3Геометрия оболочек вращения
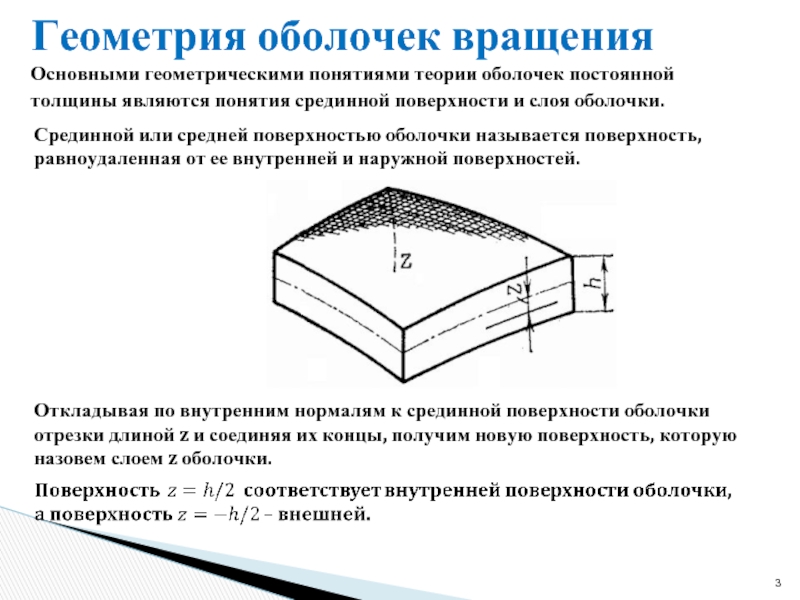
Срединной или средней поверхностью оболочки называется поверхность, равноудаленная от
Основными геометрическими понятиями теории оболочек постоянной толщины являются понятия срединной поверхности и слоя оболочки.
Откладывая по внутренним нормалям к срединной поверхности оболочки отрезки длиной z и соединяя их концы, получим новую поверхность, которую назовем слоем z оболочки.
Слайд 4Геометрия оболочек вращения
Геометрия оболочки вращения полностью определяется формой ее срединной поверхности:
сферические;
конические;
цилиндрические.
Обычно все встречающиеся на практике оболочки имеют постоянную толщину.
Слайд 5Геометрия оболочек вращения
Срединная поверхность оболочки вращения получается в результате вращения плоской
Меридианы являются линиями главных кривизн и их принимают в качестве координатных линий. Меридиан – образующая срединной поверхности.
Параллели – окружности, образованными пересечением срединной поверхности оболочки с плоскостями, перпендикулярными ее оси, – представляют семейство других координатных линий.
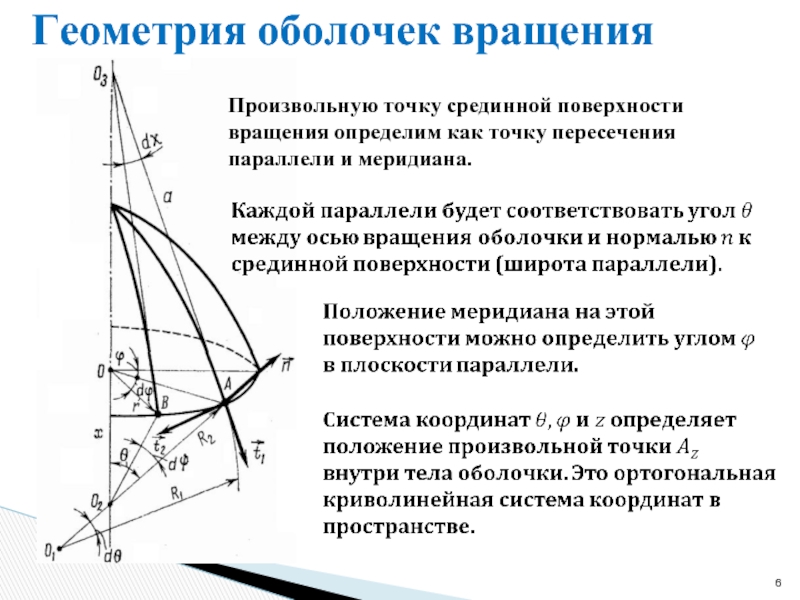
Слайд 6Геометрия оболочек вращения
Произвольную точку срединной поверхности вращения определим как точку пересечения
Слайд 10Гипотезы Кирхгофа
остается прямолинейным, нормальным к деформированной поверхности;
сохраняет свою длину.
1. Кинематическая гипотеза.
2. Статическая гипотеза.
Нормальные напряжения в площадках, параллельных поверхности отсчета, малы, и по сравнению с другими напряжениями ими можно пренебречь.
Касательные напряжения, перпендикулярные поверхности отсчета, рассматриваются как чисто статические факторы. Они определяются только из уравнений равновесия, а их связь с составляющими деформаций не учитывается.
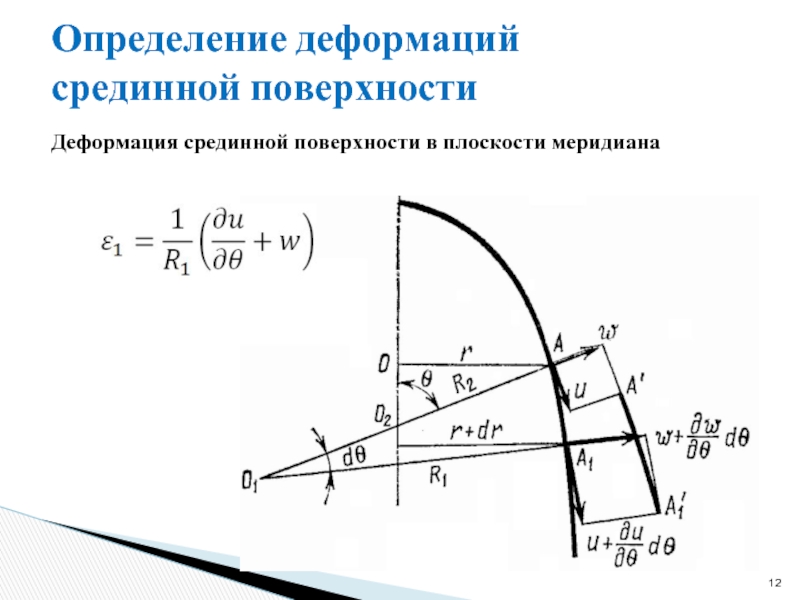
Слайд 12Определение деформаций срединной поверхности
Деформация срединной поверхности в плоскости меридиана
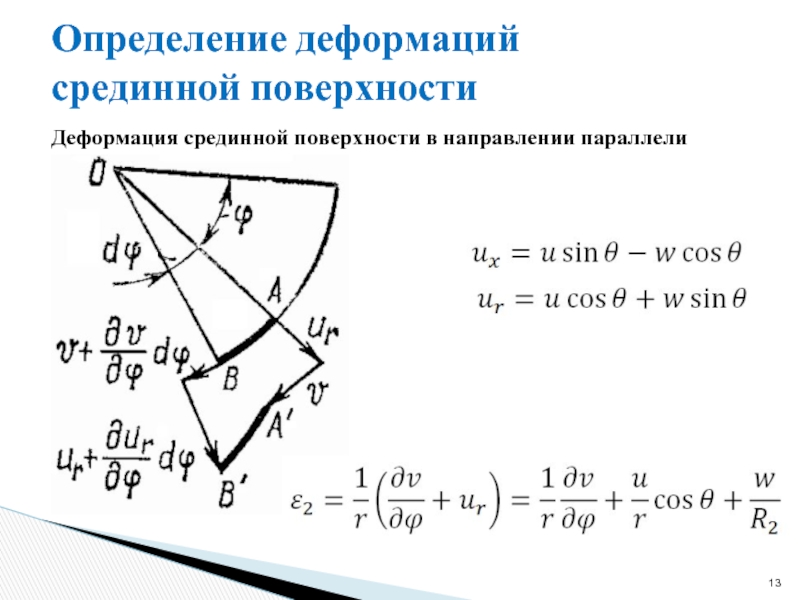
Слайд 13Определение деформаций срединной поверхности
Деформация срединной поверхности в направлении параллели
Слайд 14Определение деформаций срединной поверхности
Деформация сдвига элемента срединной поверхности оболочки
Слайд 18Безмоментная теория оболочек
Согласно этой теории считают, что изгибающие моменты равны нулю
Эта теория применима в тех случаях, когда оболочка не имеет резких переходов и закреплений и, кроме того, не нагружена сосредоточенными силами и моментами.
Безмоментная теория оболочек – приближенная теория расчета без учета изгибающих и скручивающих моментов.
При резких изменениях формы и в местах крепления возникают повышенные напряжения, обусловленные изгибным эффектом.
Для решения таких задач используется моментная теория оболочек.
Использование моментной теории показывает, что влияние этих факторов распространяется только на участки, близкие к особым точкам.
Поэтому на достаточном удалении от этих областей напряжения могут быть определены по безмоментной теории.
Слайд 19Безмоментная теория оболочек
В безмоментной теории оболочек эти напряжения считаются равномерно распределенными
Погонные усилия
Слайд 24Уравнения безмоментной теории оболочек для осесимметричной задачи
Физические соотношения
Геометрические соотношения
Слайд 25Сферическая оболочка при действии внутреннего давления
Для сферической оболочки
По условиям полной
Из уравнения Лапласа
Деформации
Перемещение
Слайд 26Цилиндрическая оболочка при действии внутреннего давления
Для цилиндрической оболочки
Из уравнения Лапласа
Кольцевое
Осевое напряжение
осевая составляющая сил давления
нормальная сила от действия напряжений
Слайд 27Цилиндрическая оболочка при действии внутреннего давления
Осевая деформации
Перемещение
Погонные усилия
Окружная деформация
Слайд 28Цилиндрическая и сферическая оболочка при действии внутреннего давления
В месте стыка цилиндра
увеличение радиуса цилиндра от действия сил давления по безмоментной теории
увеличение радиуса сферы от действия сил давления по
безмоментной теории
Стальная оболочка
Слайд 34Уравнения моментной теории оболочек
Физические соотношения (слой оболочки считают находящимся в условиях
Слайд 35Уравнения моментной теории оболочек
меридиональное погонное усилие
кольцевое погонное усилие
сдвигающее погонное
Слайд 36Уравнения моментной теории оболочек
Погонные моменты:
погонный изгибающий момент в меридиональной плоскости
погонный окружной
погонный крутящий момент
– цилиндрическая жесткость оболочки на изгиб.
Слайд 39Уравнения равновесия моментной теории оболочек
На рисунке моменты изображены в виде векторов,
Положительное направление векторов соответствует правилу правого винта.
На рисунке показаны положительные направления моментов.
Слайд 40Уравнения равновесия моментной теории оболочек
Уравнение равновесия сил в проекции на касательную
Уравнение равновесия сил в проекции на касательную к параллели
Уравнение равновесия в проекции на нормаль
Шестое уравнение равновесия элемента – равенство нулю суммы моментов относительно нормали – должно быть следствием парности касательных напряжений и выполняется автоматически.
Слайд 44Уравнения моментной теории оболочек при осесимметричной деформации
Геометрические соотношения:
Слайд 48Краевой эффект для
цилиндрической оболочки
Из второго уравнения равновесия сил для случая
Для усилия
Из уравнения