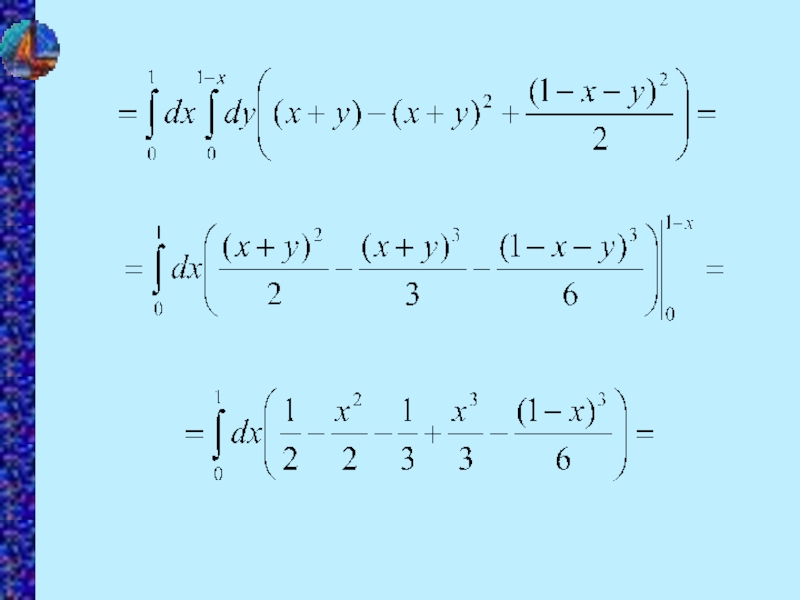- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление тройных интегралов презентация
Содержание
- 1. Вычисление тройных интегралов
- 3. 1 2 Проектируем поверхность, ограниченную
- 4. 3 Считая х,у постоянными, вычисляем интеграл: А затем двойной интеграл:
- 5. 4 Двойной интеграл можно свести к повторному:
- 6. Вычислить тройной интеграл где V –
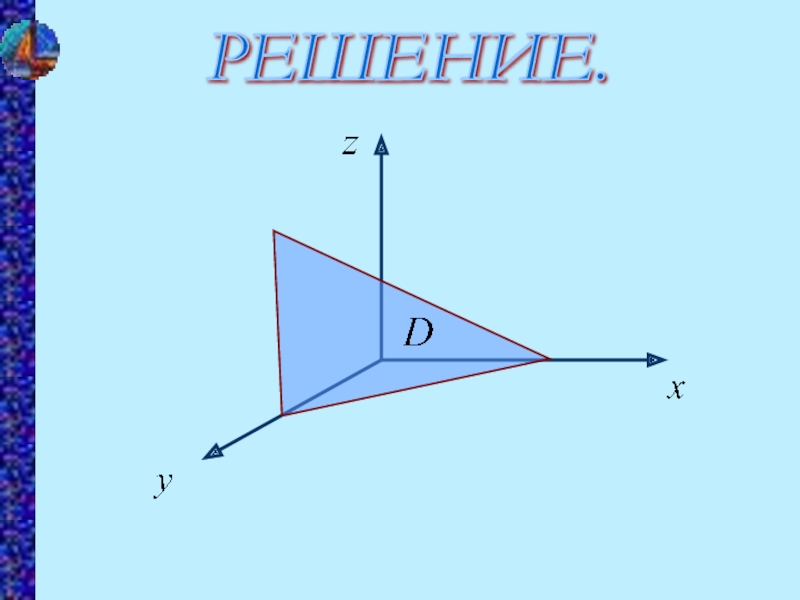
- 7. РЕШЕНИЕ.
- 8. 1 По переменной z интегрирование идет от 0 до z=1-x-y:
- 9. 2 Теперь расставляем пределы интегрирования по области D: это треугольник со сторонами x=0, y=0, x+y=1:
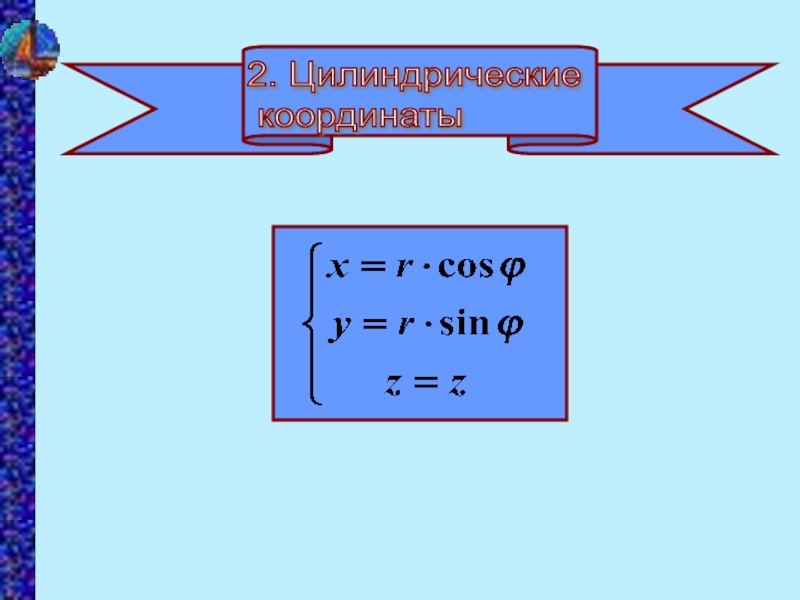
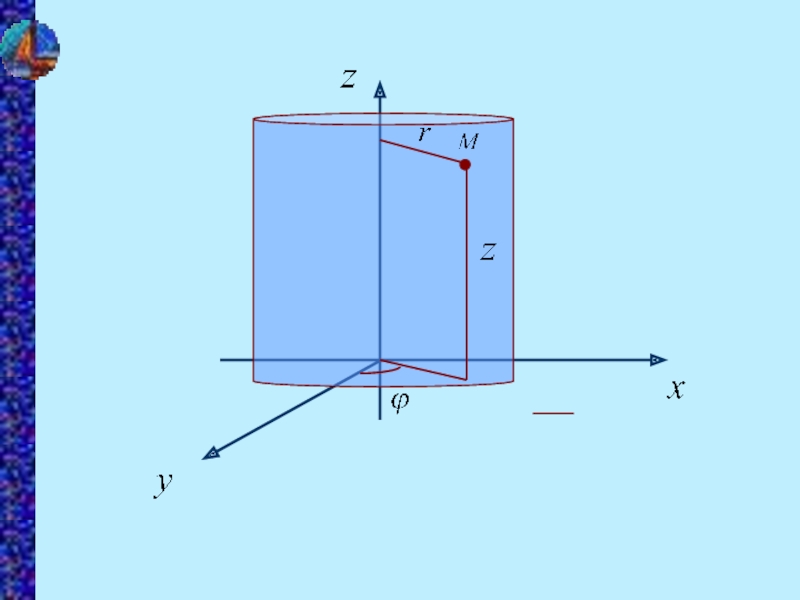
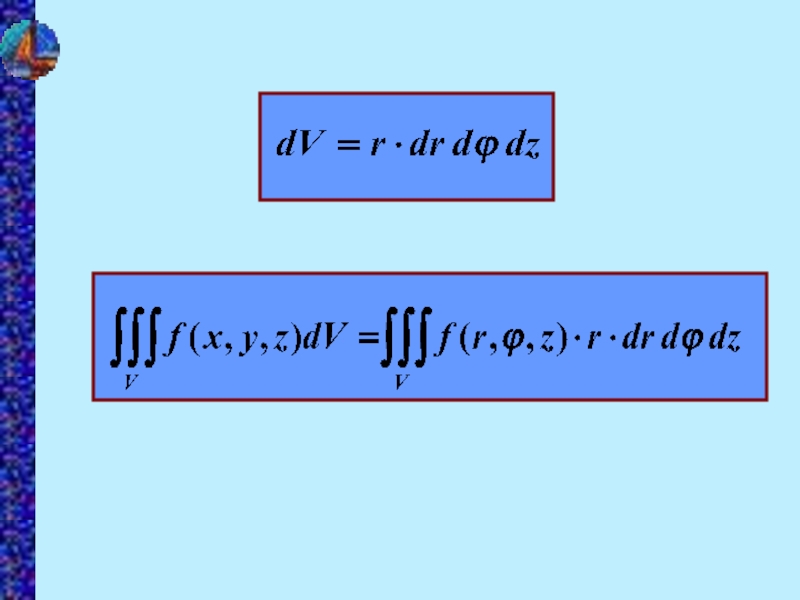
- 11. 2. Цилиндрические координаты
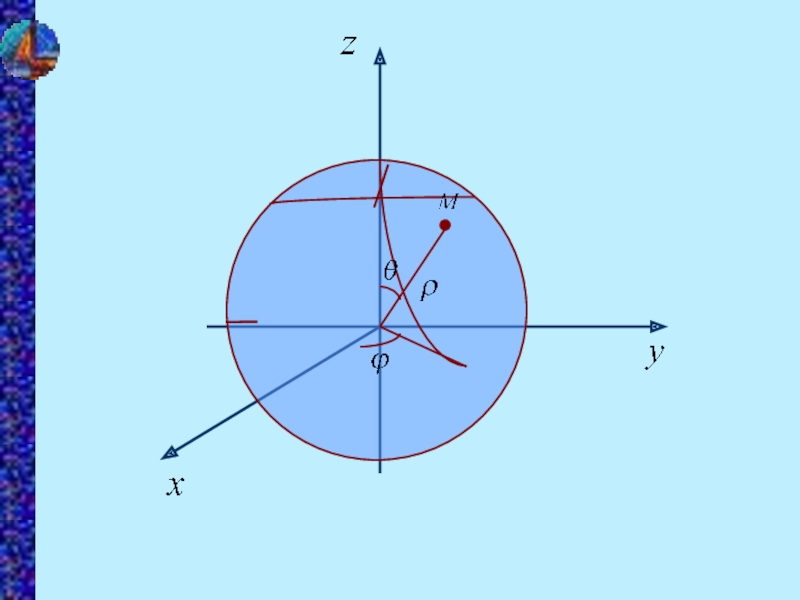
- 14. 2. Сферические координаты
1 2 Проектируем поверхность, ограниченную объемом V, на плоскость ХОУ, получаем область D. Определяем координаты точек z1 (x,y) и z2 (x,y) входа и выхода прямой, параллельной
Слайд 31
2
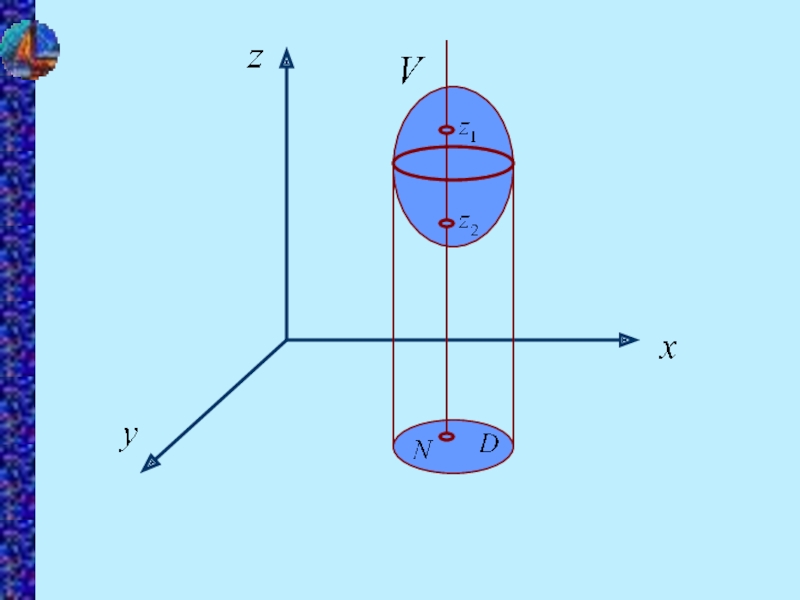
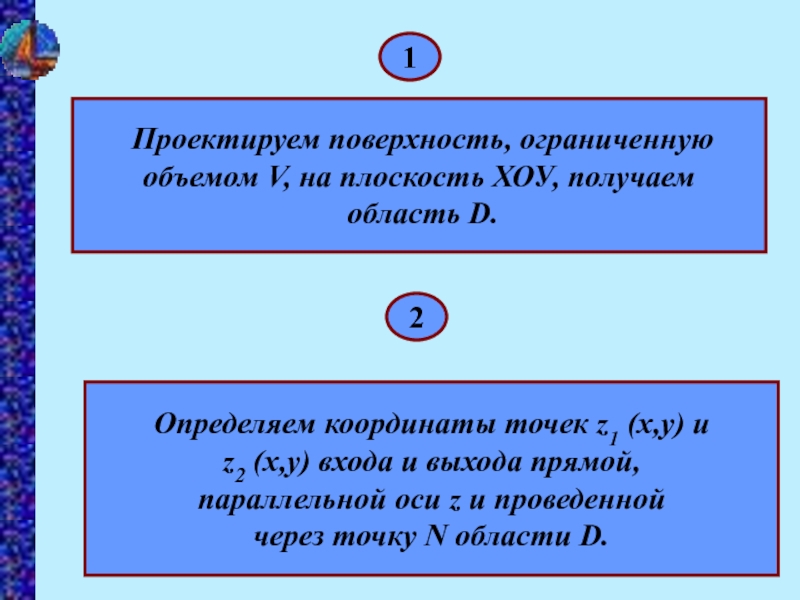
Проектируем поверхность, ограниченную
объемом V, на плоскость ХОУ, получаем
область
D.
Определяем координаты точек z1 (x,y) и
z2 (x,y) входа и выхода прямой,
параллельной оси z и проведенной
через точку N области D.
Слайд 6Вычислить тройной интеграл
где V – область, ограниченная
координатными плоскостями
x=0, у=0, z=0 и
плоскостью
x+y+z=1
x+y+z=1
ПРИМЕР.
Слайд 92
Теперь расставляем пределы интегрирования по области D: это треугольник со сторонами
x=0, y=0, x+y=1:
