- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы теории вероятностей и статистики. Решение задач на доверительные интервалы презентация
Содержание
- 1. Элементы теории вероятностей и статистики. Решение задач на доверительные интервалы
- 2. Интервальной оценкой параметра θ называется интервал
- 3. Интервальные оценки параметров
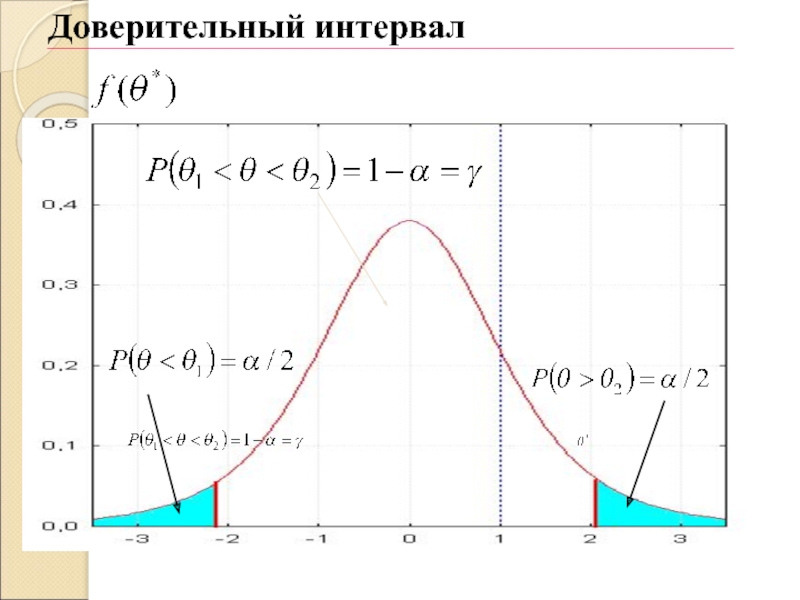
- 4. Доверительный интервал
- 5. 3 типа задач на доверительные интервалы (ДИ)
- 6. Доверительный интервал для МО нормальной СВ при известной генеральной дисперсии 2) 1) 3) 4) 5)
- 7. Точность (предельная погрешность) оценки МО: 1) 2)
- 8. Задача №1 3. Определяем ДИ для
- 10. 2. Доверительный интервал для мат. ожидания нормальной
- 11. Точность (предельная погрешность) оценки МО: 1) 2)
- 12. 1) 2) Доверительный интервал для прогнозируемого МО
- 13. Задача №2 3. Определяем ДИ для
- 14. Задача №2 4. Вычисление прогноза
- 16. 3. Доверительный интервал для дисперсии нормальной СВ
- 17. Задача №2 3. Определяем ДИ для
Слайд 2Интервальной оценкой параметра θ называется интервал (θ1, θ2), который с
Интервал (θ1, θ2) называется доверительным интервалом, а вероятность – доверительной вероятностью (надежность. доверительного интервала).
Вероятность называется уровнем значимости.
Выборочные оценки параметров являются СВ.
На основании выборочных оценок можно установить интервалы, внутри которых с некоторой вероятностью находятся истинные значения параметров.
Интервальные оценки параметров
Слайд 53 типа задач на доверительные интервалы (ДИ)
1. Построение ДИ для математического
2. Построение ДИ для математического ожидания при неизвестной генеральной дисперсии (СКО), но известной исправленной выборочной дисперсии (СКО)
3. Построение ДИ для генеральной дисперсии (СКО) при известной выборочной исправленной дисперсии (СКО)
Слайд 8
Задача №1
3. Определяем ДИ для МО
1. Находим критическую точку СНЗР
2. Вычисляем
n=25, X~N(m, 10).
Слайд 9
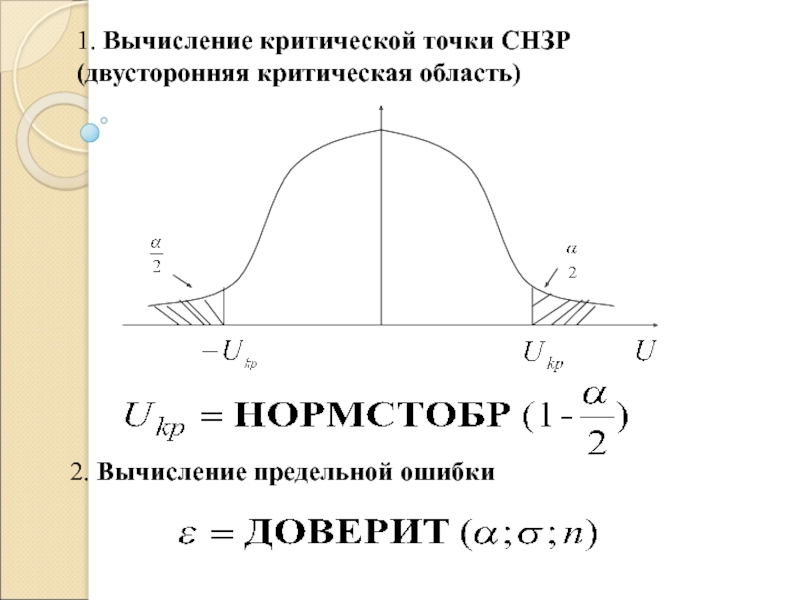
1. Вычисление критической точки СНЗР
(двусторонняя критическая область)
2. Вычисление предельной ошибки
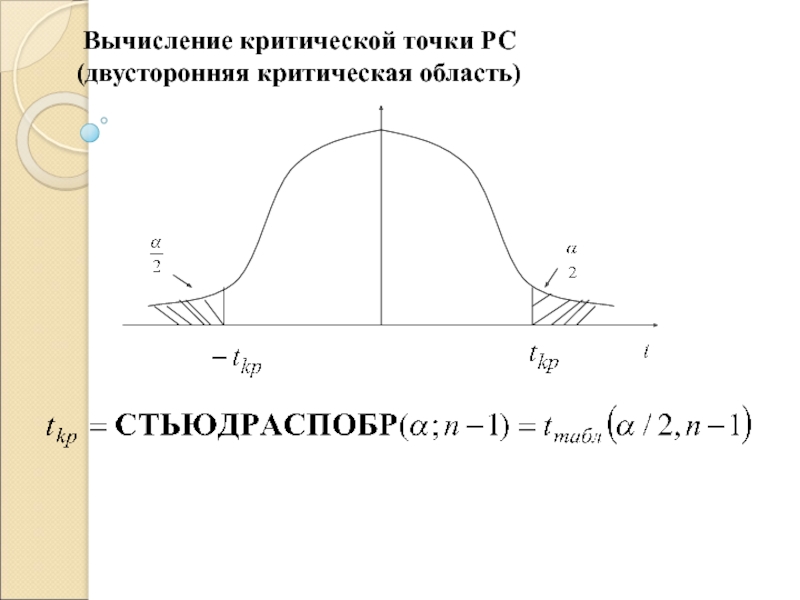
Слайд 102. Доверительный интервал для мат. ожидания нормальной СВ при неизвестной генеральной
- Распределение Стьюдента с n-1 степенями свободы
1)
4)
3)
2)
Слайд 121)
2)
Доверительный интервал для прогнозируемого
МО нормальной СВ при неизвестной дисперсии
Доверительный интервал:
Задана
Построить доверительный интервал для
Построить доверительный интервал для
Слайд 13
Задача №2
3. Определяем ДИ для МО
1. Находим критическую точку РC
2. Вычисляем
n=55, X~T(α, n-1).
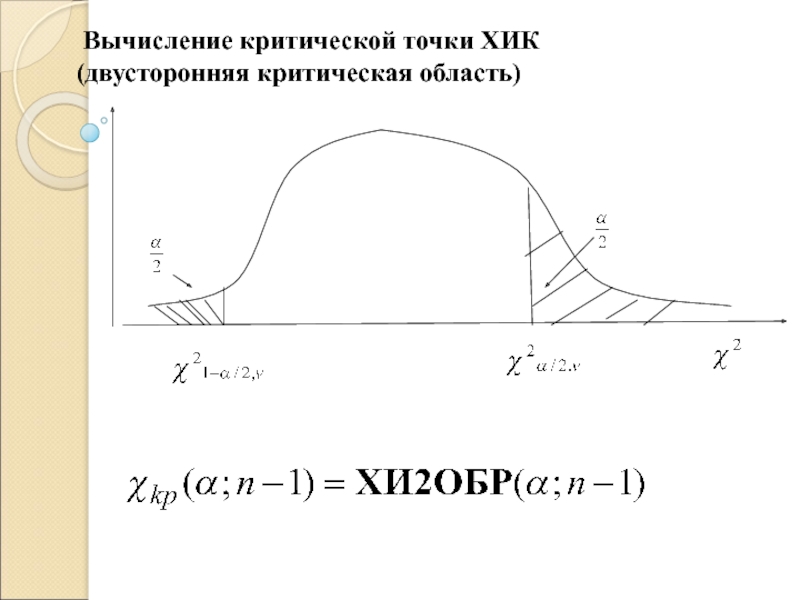
Слайд 163. Доверительный интервал для дисперсии нормальной СВ при неизвестном МО
- Распределение
1)
2)
3)
4)
Слайд 17
Задача №2
3. Определяем ДИ для СКО
1. Находим критические точки РХК
2. Определяем
n=10, x~χ2(α, n-1).