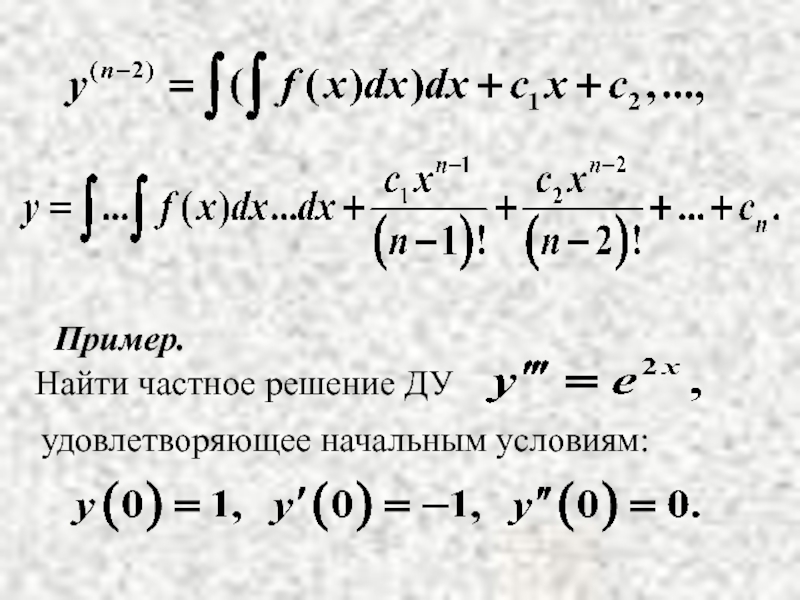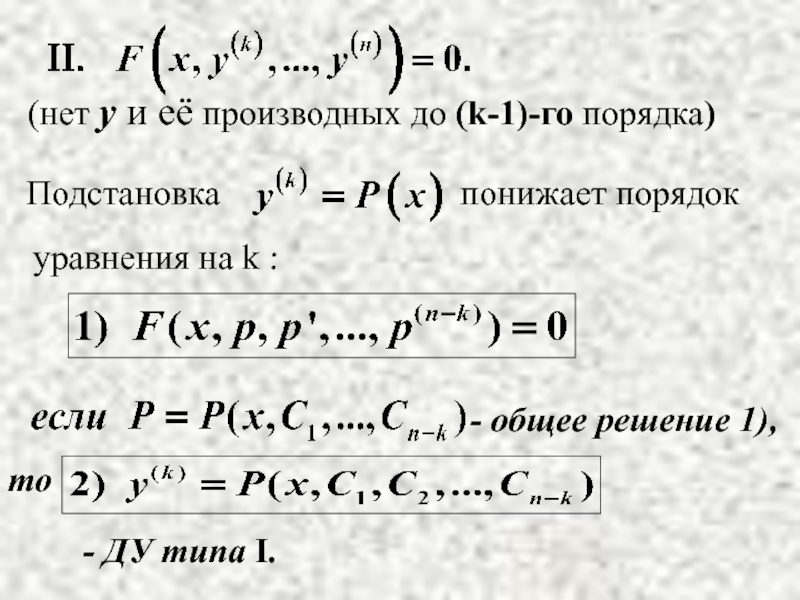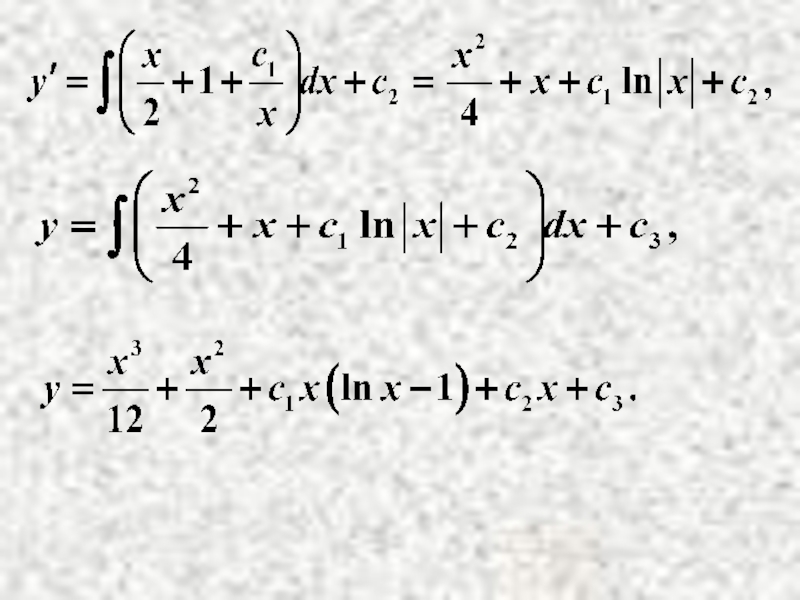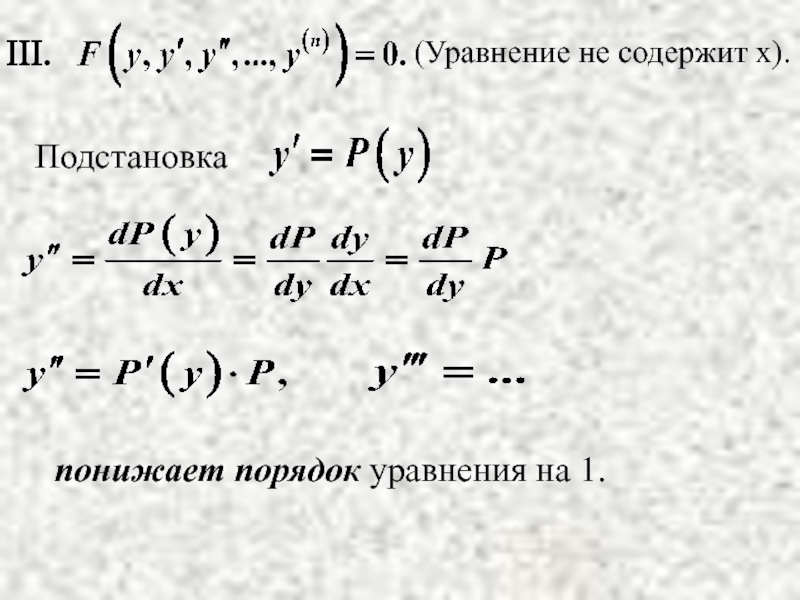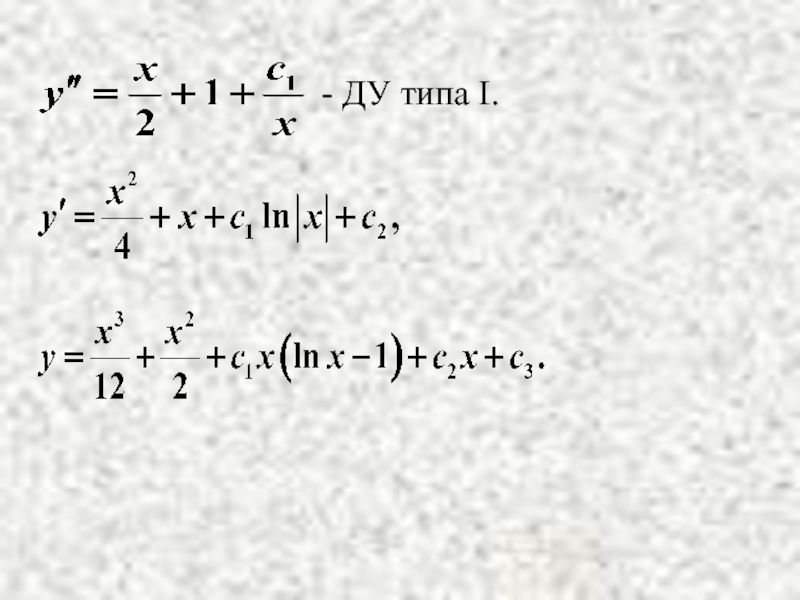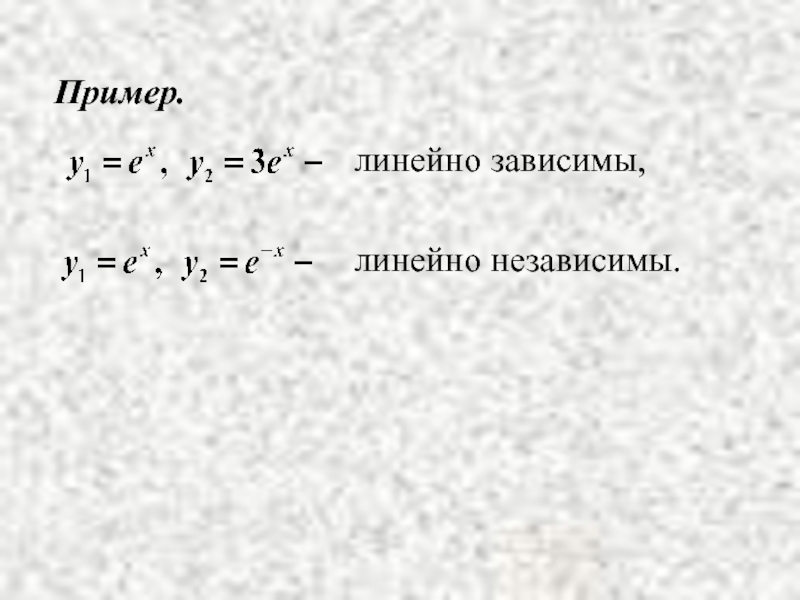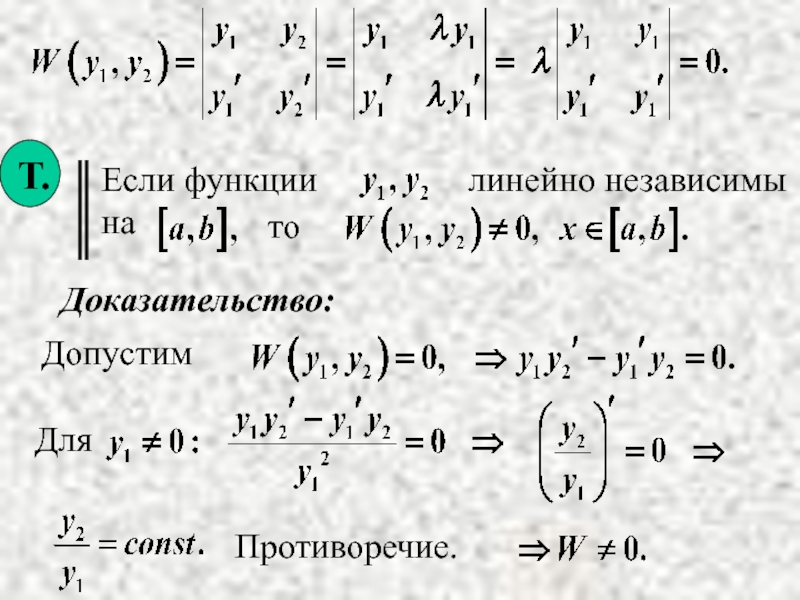- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДУ высших порядков. Задача Коши для уравнения порядка n презентация
Содержание
- 1. ДУ высших порядков. Задача Коши для уравнения порядка n
- 2. Требуется найти решение ДУ n-го порядка
- 4. Частное решение ДУ (решение задачи Коши) может
- 5. Решение задачи Коши ДУ n-го порядка имеет
- 6. (правая часть зависит только от х) Общее решение получается путем n-кратного интегрирования:
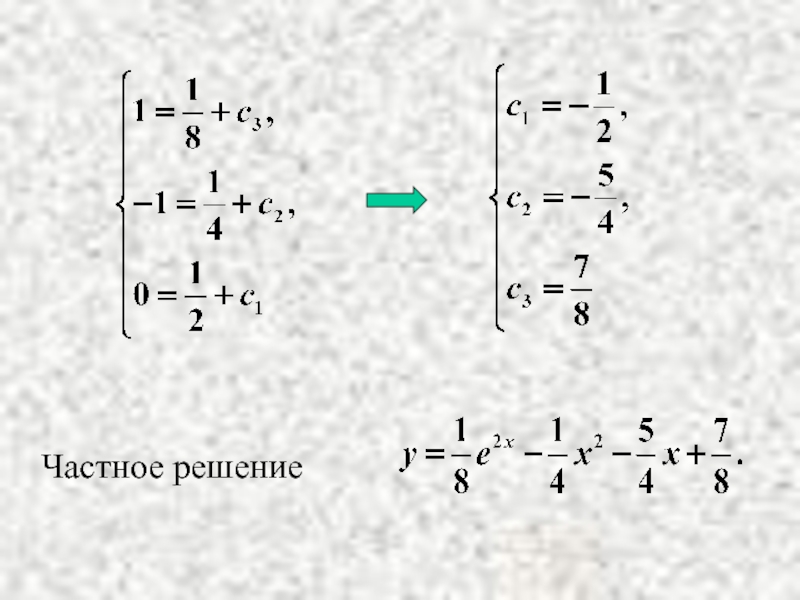
- 7. Пример. удовлетворяющее начальным условиям:
- 8. Решение.
- 9. Частное решение
- 10. Подстановка
- 11. Пример . Решение.
- 13. (Уравнение не содержит х). понижает порядок уравнения на 1.
- 14. Пример . Решение.
- 16. Интегрирование понижает порядок уравнения на единицу. Пример. Решение.
- 17. - ДУ типа I.
- 19. Линейное дифференциальное уравнение называется неоднородным (НЛДУ) если оно имеет вид:
- 20. Рассмотрим ОЛДУ второго порядка: - частные решения ДУ.
- 21. Пример. линейно зависимы, линейно независимы.
- 22. то называется определителем Вронского. Доказательство:
- 23. то Допустим Доказательство: Противоречие.
- 24. то общее решение этого Доказательство: уравнения равно их линейной комбинации:
- 25. Докажем, что при любых начальных условиях удовлетворяло этим начальным условиям. Пусть
Слайд 2Требуется найти решение ДУ n-го порядка
удовлетворяющего заданным начальным условиям:
Лекция 12
ДУ высших порядков.
Слайд 4Частное решение ДУ (решение задачи Коши) может быть найдено из общего
решения по заданным начальным условиям, из которых получают систему уравнений для определения постоянных
Слайд 6 (правая часть зависит только от х)
Общее решение получается путем
n-кратного интегрирования: