- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дробно-факторный эксперимент (ДФЭ) презентация
Содержание
- 1. Дробно-факторный эксперимент (ДФЭ)
- 2. К матрице ДФЭ предъявляют те же требования,
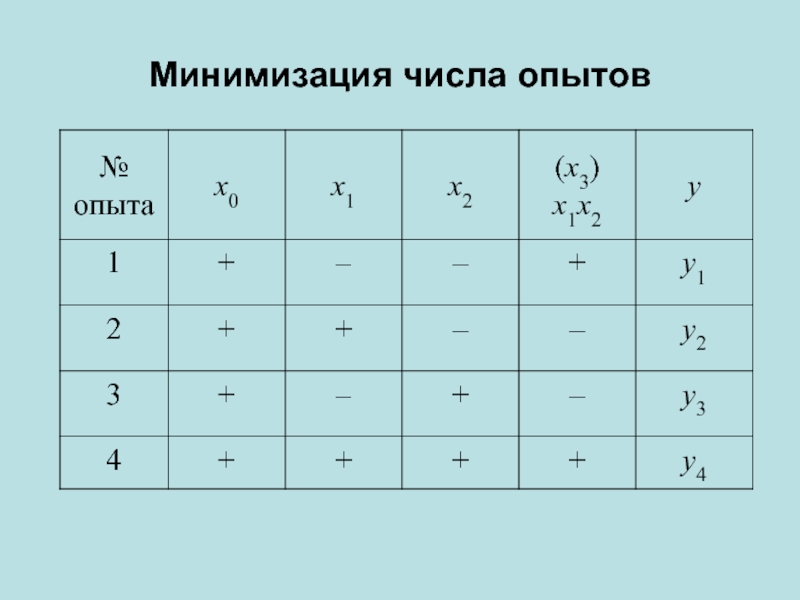
- 3. Минимизация числа опытов
- 4. Пользуясь таким планированием, можно вычислить
- 5. Посмотрим, каковы будут оценки коэффициентов в этом
- 6. Чтобы сократить число опытов, нужно новому фактору
- 7. Если бы мы х3 приравняли к
- 8. Матрица из восьми опытов для четырех факторного
- 9. Для обозначения дробных реплик, в
- 10. Для произведения трех столбцов первой матрицы выполняется
- 11. Символическое обозначение произведения столбцов, равного
- 12. Это значит, что коэффициенты линейного уравнения будут
- 13. Соотношение, показывающее, с каким из
- 14. Разрешающая способность этих полуреплик различна 1.
- 15. Разрешающая способность задается системой смешивания данной реплики.
- 16. При отсутствии априорной информации об эффектах
- 17. Реплики, в которых нет ни одного главного
- 18. х5 можно приравнять к одному из 6 парных
- 19. Полуреплика может быть задана генерирующими соотношениями
- 20. Полурепликами 26-1 редко пользуются на практике, т.к.
- 21. При исследовании влияния пяти
- 22. Чтобы полностью охарактеризовать разрешающую способность реплики, необходимо записать обобщающий определяющий контраст
- 23. Пример. Методом дробных реплик найти математическое
- 24. Перемножив их почленно, получим новые определяющие контрасты.
- 25. 3. Составим алгебраическую сумму из единицы и
- 26. Если поверхность отклика не может
- 27. Различают два вида центрального
- 28. Значения «звездного» плеча α для
- 29. Переменные величины введены для того,
- 30. Чтобы получить уравнение регрессии в обычной форме находят величину
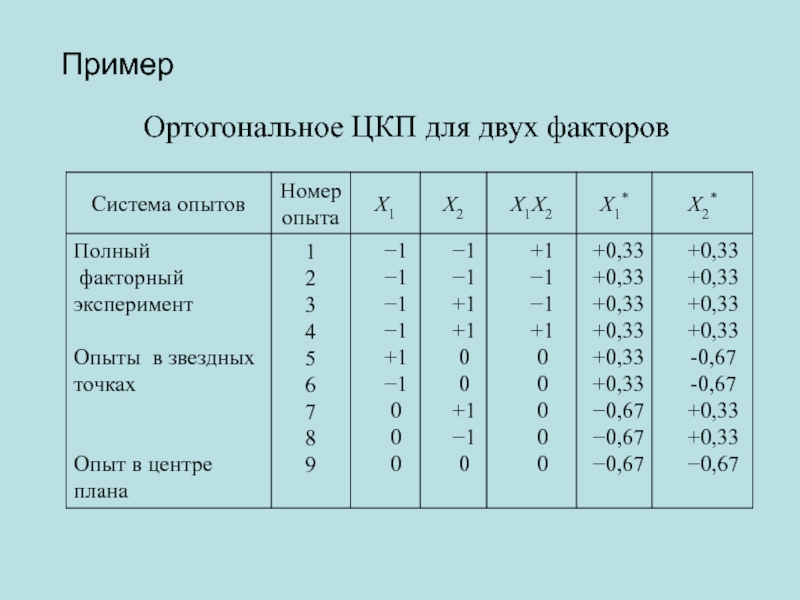
- 31. Ортогональное ЦКП для двух факторов Пример
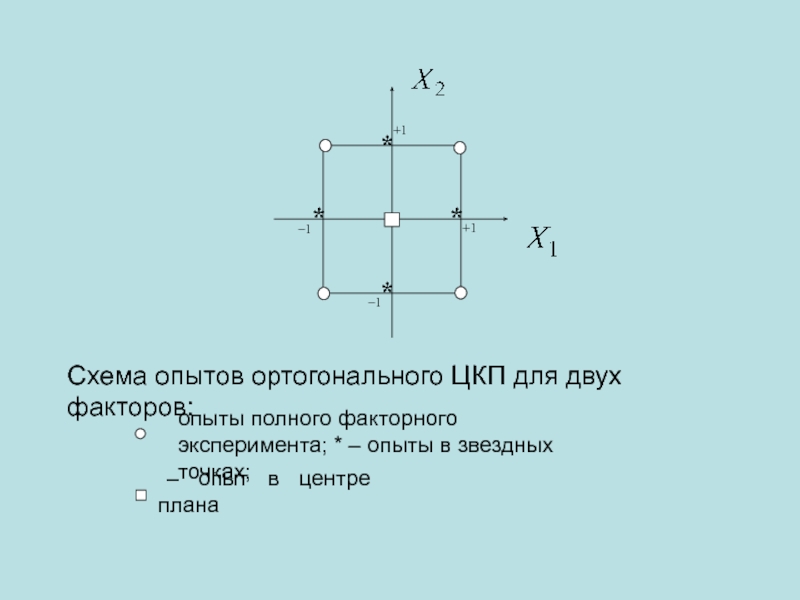
- 32. Схема опытов ортогонального ЦКП для
- 33. где i ≠ 0 Коэффициенты
- 34. где i ≠ 0
- 35. Коэффициент bi, считается значимым, если
- 36. Это план 2-ого порядка после преобразований (*)
- 37. Метод ротатабельного планирования эксперимента
- 38. Это план, у которого
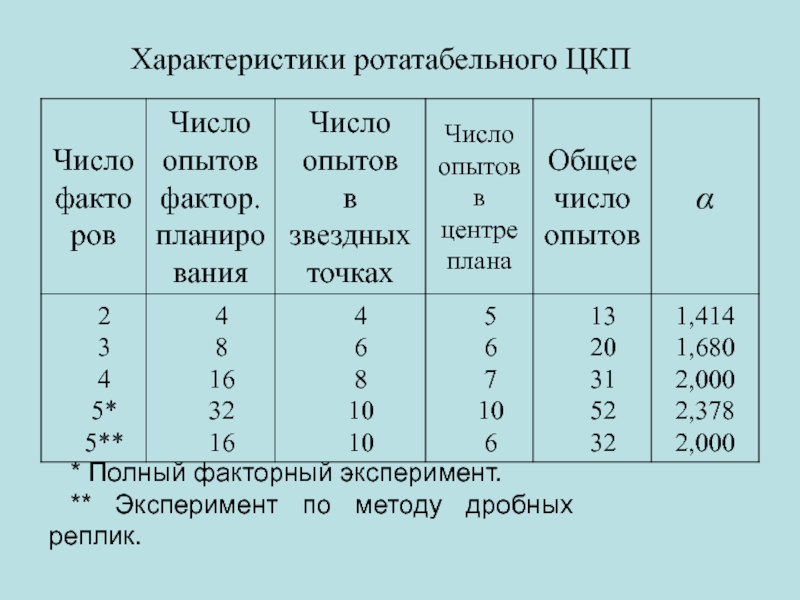
- 39. Характеристики ротатабельного ЦКП * Полный факторный эксперимент. ** Эксперимент по методу дробных реплик.
- 40. При ротатабельном ЦКП для вычисления
- 41. На основании результатов эксперимента вычисляют следующие
- 42. Формулы для расчета коэффициентов регрессии имеют следующий вид где i ≠ k
- 43. Оценки дисперсий в определении коэффициентов регрессии
- 44. Коэффициент bi, считается значимым, если
- 45. С ней связано число степеней свободы Проверку
- 46. Ротабельный план 2-ого порядка Для
- 47. Пример. Рассмотреть ротатабельное ЦКП для двух
- 48. Для нахождения коэффициентов регрессии вычислим следующие вспомогательные
- 52. Оценку дисперсии воспроизводимости можно найти на основании
- 54. Пользуясь таблицей значений критерия
- 55. Все коэффициенты регрессии значимы. Вычисляем оценку дисперсии адекватности
- 56. Число степеней свободы, связанных с этой оценкой
- 57. адекватно представленным результатам эксперимента Перейдем в
- 58. Подставляя их в полученное в этом примере
Слайд 1Дробно-факторный эксперимент (ДФЭ)
При многофакторном эксперименте, особенно когда число факторов больше шести
ДФЭ может содержать половину, четверть и т.д. опытов от ПФЭ
Слайд 2К матрице ДФЭ предъявляют те же требования, что и к матрице
Планы ДФЭ 2n-k, где k - показатель дробности плана ПФЭ. При k=1 число опытов в плане ДФЭ в два раза меньше чем в плане ПФЭ, поэтому такие планы называют полурепликой плана ПФЭ, при k=2 – четвертьрепликой плана ПФЭ
Слайд 4 Пользуясь таким планированием, можно вычислить четыре коэффициента и представить
Если в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента b0, b1, b2. При линейном приближении b12→0 и вектор-столбец x1x2 можно использовать для нового фактора x3
Слайд 5Посмотрим, каковы будут оценки коэффициентов в этом случае. Здесь уже не
b1 → β1 + β23, b2 → β2 + β13, b3 → β3 + β12
Вместо 8 опытов для изучения 3 факторов можно поставить 4
Матрица планирования не теряет своих оптимальных свойств
Слайд 6Чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий
Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной полного факторного эксперимента 23 или «полурепликой».
Слайд 7 Если бы мы х3 приравняли к –x1x2, то получили бы
b1 → β1 - β23, b2 → β2 - β13, b3 → β3 - β12
Объединение этих двух полуреплик и есть полный факторный эксперимент 23, отражающий и линейные эффекты и эффекты взаимодействия
Слайд 8Матрица из восьми опытов для четырех факторного планирования будет полурепликой от
В четвертьреплике два линейных эффекта приравниваются к эффектам взаимодействия
Слайд 9 Для обозначения дробных реплик, в которых p линейных эффектов приравнены к
При построении полуреплики 23-1 существует только две возможности приравнять х3 к х1х2 или –х1х2. Поэтому есть только две полуреплики 23-1
Слайд 10Для произведения трех столбцов первой матрицы выполняется соотношение: +1 = х1х2х3,
Слайд 11 Символическое обозначение произведения столбцов, равного +1 или –1, называется определяющим
Контраст помогает определять смешанные эффекты. Для того чтобы определить, какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту.
Слайд 12Это значит, что коэффициенты линейного уравнения будут оценками:
х1 = х1х1х2х3
Если контраст +1, то для х1 имеем
для х2 имеем
х2 = х1х2х2х3 = х1х3
для х3 имеем
х3 = х1х2х3х3 = х1х2
b1 → β1 + β23, b2 → β2 + β13, b3 → β3 + β12
Слайд 13 Соотношение, показывающее, с каким из эффектов смешан данный эффект,
Полуреплики, в которых основные эффекты смешаны с двухфакторными взаимодействиями, носят название планов с разрешающей способностью III (по наибольшему числу факторов в определяющем контрасте).Такие планы принято обозначать:
Слайд 14Разрешающая способность этих полуреплик различна
1. х4 = х1х2
При выборе
3. х4 = х2х3
7. х4 = х1х2х3
2. х4 = –х1х2
4. х4 = –х2х3
5. х4 = х1х3
6. х4 = – х1х3
8. х4 = – х1х2х3
Слайд 15Разрешающая способность задается системой смешивания данной реплики. Она будет максимальной, если
Реплики 7 и 8 имеют максимальную разрешающую способность и называются главными
Реплики 1 – 6 имеют по три фактора в определяющем контрасте, а 7 – 8 по четыре.
Слайд 16
При отсутствии априорной информации об эффектах взаимодействия экспериментатор стремится выбрать реплику
Слайд 17Реплики, в которых нет ни одного главного эффекта, смешанного с другим
Такие полуреплики называют главными полурепликами, так как они обладают наибольшей разрешающей способностью
Слайд 18х5 можно приравнять к одному из 6 парных взаимодействий. В этом случае
При выборе полуреплики 25-1 в распоряжении экспериментатора имеется множество вариантов
х5 можно приравнять к одному из четырех тройных взаимодействий. Тогда получим план с разрешающей способностью IV, и все линейные эффекты будут смешаны с тройными взаимодействиями
Слайд 19
Полуреплика может быть задана генерирующими соотношениями
Определяющими контрастами в этом случае будут
и
Слайд 20
Полурепликами 26-1 редко пользуются на практике, т.к. такая полуреплика требует 32 опыта,
При построении главных полуреплик в определяющий контраст надо включать наибольшее число факторов
Слайд 21
При исследовании влияния пяти факторов можно поставить не 16
и
Тогда определяющими контрастами являются
или
Слайд 22
Чтобы полностью охарактеризовать разрешающую способность реплики, необходимо записать обобщающий определяющий контраст
Слайд 23
Пример. Методом дробных реплик найти математическое описание процесса в виде уравнения
Выбор генерирующих соотношений в общем случае произволен, однако он существенно влияет на характер совместных оценок коэффициентов регрессии.
Правило определения совместных оценок коэффициентов состоит в следующем
Воспользуемся планированием типа 25−2 и примем генерирующие соотношения
Слайд 24Перемножив их почленно, получим новые определяющие контрасты. В данном случае это
1.
2. Умножив обе части генерирующих соотношений соответственно на X4 и X5, получим
определяющие контрасты
Слайд 253. Составим алгебраическую сумму из единицы и правых частей всех полученных
4. Умножив каждый из факторов на S и заменив факторы соответствующими коэффициентами разложения в ряд Тейлора, получим
Слайд 26 Если поверхность отклика не может быть описана многочленом вида
Метод ортогонального центрального композиционного планирования
для адекватного математического описания используется многочлен более высокой степени, например, отрезок ряда Тейлора, содержащий члены с квадратами переменных. Тогда используют центральное композиционное планирование (ЦКП) эксперимента
Слайд 27
Различают два вида центрального композиционного планирования (ЦКП):
здесь 2n – количество опытов, образующих полный факторный эксперимент; 2n – число так называемых «звездных» точек в факторном пространстве, имеющих координаты (±α, 0, 0, ..., 0); (0, ±α, 0, ..., 0), ..., (0, 0, ..., ±α). Здесь величина α называется «звездным» плечом;
1 – опыт в центре планирования, т. е. в точке факторного пространства с координатами (0, 0, ..., 0)
Количество опытов при ортогональном ЦКП определяется по формуле
Слайд 28 Значения «звездного» плеча α для ЦКП с различным числом
Эти значения α выбраны из условия ортогональности матрицы планирования
Слайд 29Переменные величины
введены для того, чтобы матрица планирования была ортогональна и
здесь j – номер опыта; i – номер фактора
Уравнение регрессии при ортогональном ЦКП ищут в следующем виде
Слайд 32
Схема опытов ортогонального ЦКП для двух факторов:
опыты полного факторного эксперимента; *
– опыт в центре плана
Слайд 33где i ≠ 0
Коэффициенты регрессии при ортогональном ЦКП считают по
где i ≠ k
Слайд 34где i ≠ 0
Для расчета оценок дисперсий в
где i ≠ k
Слайд 35
Коэффициент bi, считается значимым, если
Аналогично проверяется значимость остальных коэффициентов регрессии.
Проверка адекватности уравнения регрессии осуществляется с помощью критерия Фишера
Слайд 36Это план 2-ого порядка после преобразований (*)
Эти преобразования позволяют усреднить случайные
Ортогональный план
Ортогональный план 2-ого порядка
Тогда уравнение регрессии
В итоге уравнение регрессии преобразуется к виду
Слайд 37 Метод ротатабельного планирования эксперимента позволяет получать более точное
Метод ротатабельного центрального композиционного планирования
Слайд 38
Это план, у которого точки плана располагаются на окружностях
Точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая, что позволяет наилучшим образом извлечь максимальное количество (несмещенной) информации из плана
Слайд 39Характеристики ротатабельного ЦКП
* Полный факторный эксперимент.
** Эксперимент по методу дробных реплик.
Слайд 40 При ротатабельном ЦКП для вычисления коэффициентов регрессии и соответствующих
где n – число факторов; N – общее число опытов ротатабельного ЦКП; N0 – число опытов в центре плана
Слайд 41
На основании результатов эксперимента вычисляют следующие суммы
(где i=1,2,…,n),
(где i
(где i=1,…, n)
Слайд 43
Оценки дисперсий в определении коэффициентов регрессии вычисляют по следующим формулам
(где
(где i≠k)
Слайд 44Коэффициент bi, считается значимым, если
Аналогично проверяется значимость остальных коэффициентов регрессии
Оценку дисперсии адекватности рассчитывают по формуле
Слайд 45С ней связано число степеней свободы
Проверку адекватности уравнения регрессии осуществляют с
Слайд 46Ротабельный план 2-ого порядка
Для того, что бы привести план
Слайд 47
Пример. Рассмотреть ротатабельное ЦКП для двух факторов. Матрица планирования и результаты
Матрица планирования и результаты эксперимента
Слайд 48Для нахождения коэффициентов регрессии вычислим следующие вспомогательные коэффициенты
На основании результатов
Слайд 52Оценку дисперсии воспроизводимости можно найти на основании результатов опытов, проведенных в
Эта величина найдена при числе степеней свободы
Оценки дисперсий в определении коэффициентов регрессии
Слайд 54 Пользуясь таблицей значений критерия Стьюдента, находим
для
Для проверки значимости коэффициентов регрессии рассмотрим соотношения:
Слайд 56Число степеней свободы, связанных с этой оценкой дисперсии
Расчетное значение критерия
Из таблицы значений критерия Фишера соответствующее значение критерия . Условие выполнено, следовательно, уравнение регрессии
Слайд 57адекватно представленным результатам эксперимента
Перейдем в уравнение регрессии от кодированных переменных
Пусть в нашем примере кодированные переменные X1 и X2 представляют собой температуру и концентрацию, причем координаты центра плана
x01= 60°С и x02= 30%, а шаги варьирования Δx1= 5°С и Δх2= 1% . Тогда
Слайд 58Подставляя их в полученное в этом примере уравнение регрессии, преобразуем его
Пользуясь таким уравнением, исследователь избавляется от необходимости переводить всякий раз условия опыта в кодированные переменные