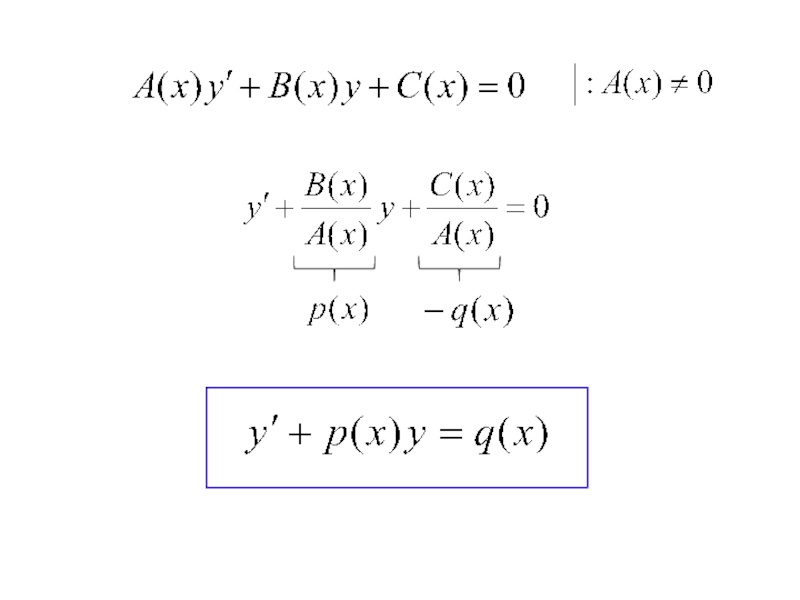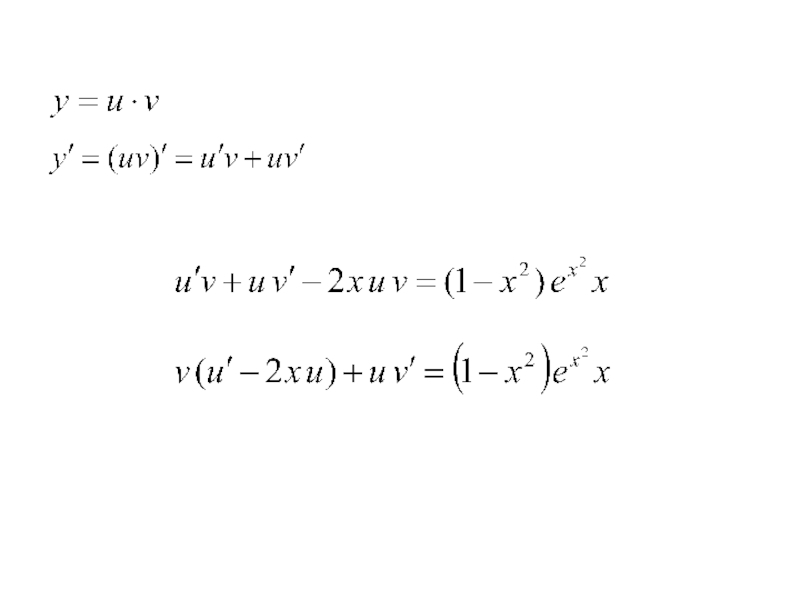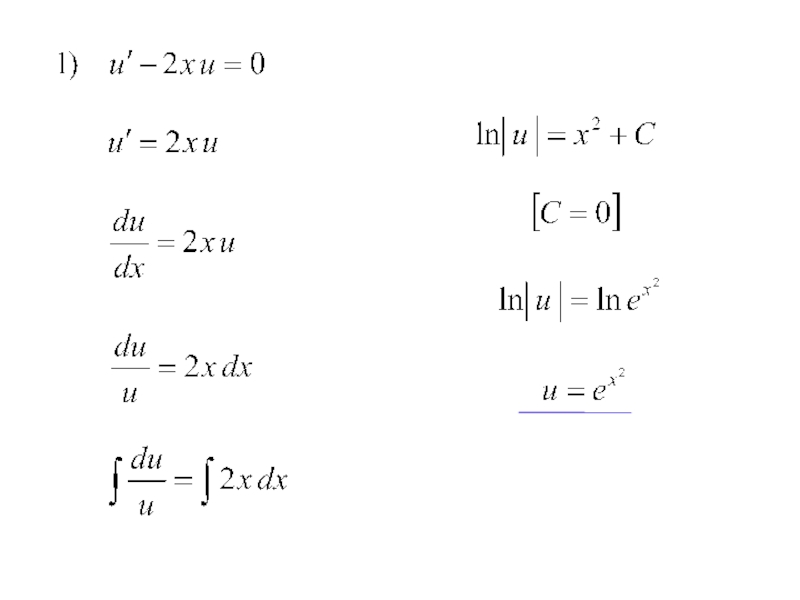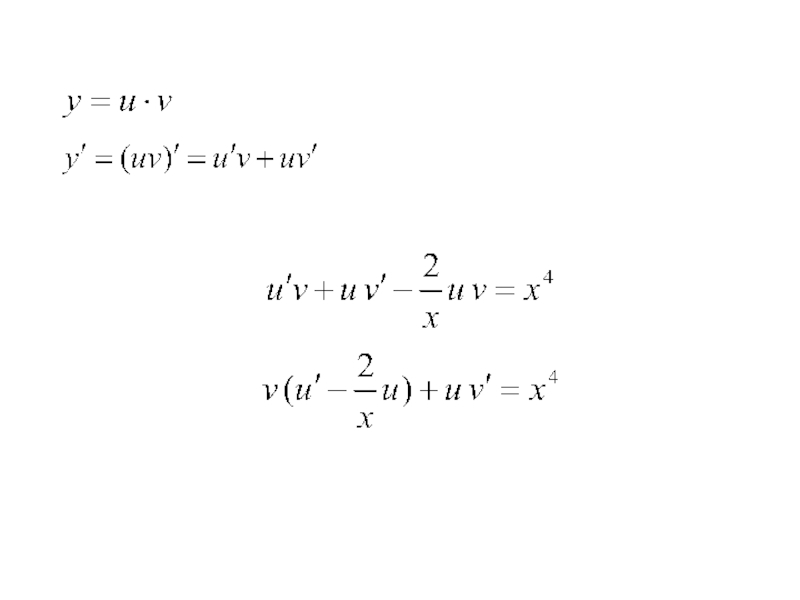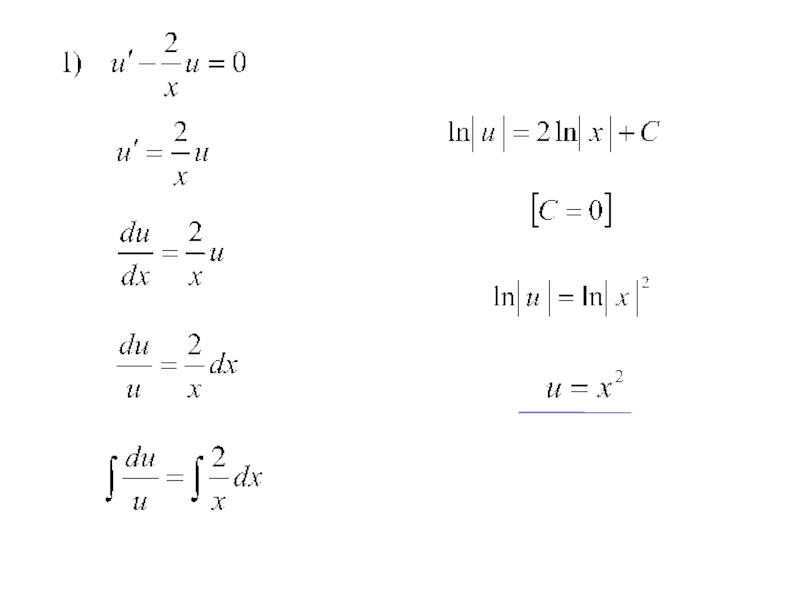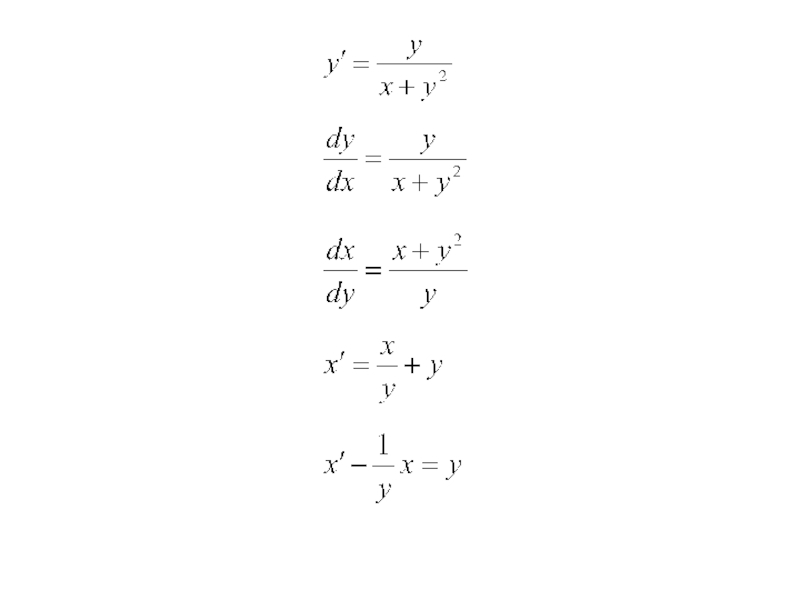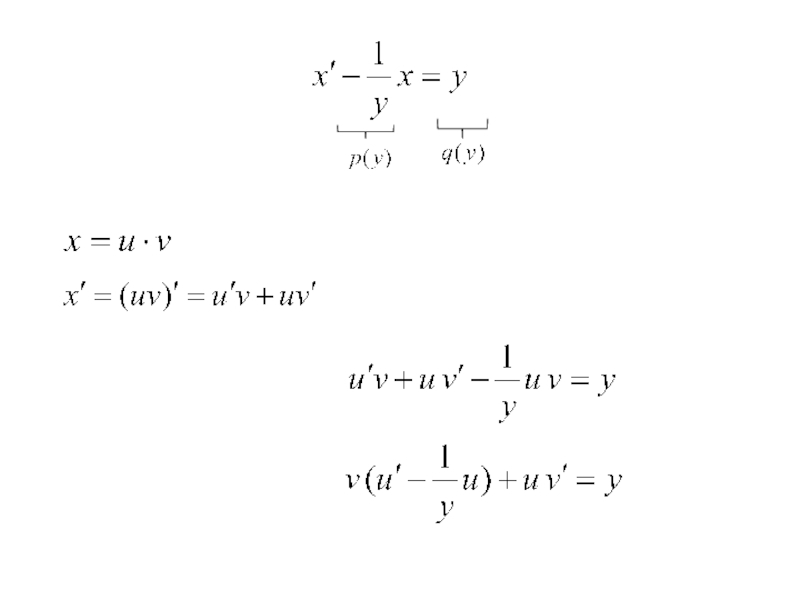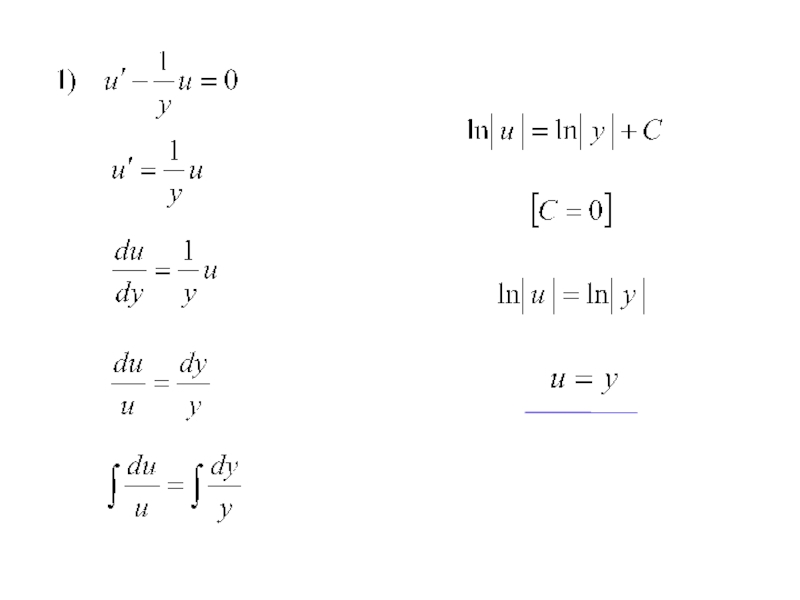- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальные уравнения-4 презентация
Содержание
- 1. Дифференциальные уравнения-4
- 2. 5. Линейные ДУ I порядка.
- 4. Существует несколько (по существу равносильных) приёмов решения
- 5. Метод И.Бернулли основан на простом замечании, что
- 6. Например: можем взять или или или соответственно этому придется взять
- 7. Пример 1. Найти общее решение ДУ:
- 8. Найдём производную: Подставим её в уравнение: Используем
- 10. Поскольку в качестве u нам надо взять
- 11. Подставляя в уравнение (*) и учитывая, что , получим:
- 12. Общее решение ДУ: или Ответ. Общее решение ДУ:
- 13. Изложим приём в общем виде:
- 14. Найдём производную: Подставим её в уравнение: Используем
- 16. Поскольку в качестве u нам надо взять
- 17. Подставляя в уравнение
- 18. Общее решение ДУ: Ответ. Общее решение ДУ:
- 19. Пример 2. Найти общее решение ДУ: Решение:
- 21. 3) Общее решение ДУ: Ответ. Общее решение ДУ:
- 22. Пример 3. Найти общее решение ДУ: Нужно привести к виду Решение:
- 25. 3) Общее решение ДУ: Ответ. Общее решение ДУ:
- 26. Пример 4. Решить задачу
- 29. 3) Общее решение ДУ:
- 30. Найдем частное решение ДУ: Подставим начальные условия
- 31. Пример 5. Найти общее решение ДУ:
- 35. 3) Общее решение ДУ: Ответ. Общее решение ДУ:
5. Линейные ДУ I порядка. Общий вид линейного ДУ I порядка: А(х), В(х) и С(х)- заданные функции, причем
Слайд 25. Линейные ДУ I порядка.
Общий вид линейного ДУ I порядка:
А(х), В(х)
и С(х)- заданные функции, причем
Слайд 4 Существует несколько (по существу равносильных) приёмов решения линейного ДУ.
Рассмотрим метод Иоганна
Бернулли (Bernoulli)- швейцарский математик 1667-1748.
Слайд 5 Метод И.Бернулли основан на простом замечании, что любую величину h (переменную
или постоянную) можно представить в форме произведения двух сомножителей: h=uv [u=u(x), v=v(x)], причем один из них можно выбрать по своему желанию, но отличным от нуля.
Слайд 7Пример 1. Найти общее решение ДУ:
Это линейное ДУ вида
Представим (неизвестное
нам!) общее решение ДУ в виде:
Слайд 8Найдём производную:
Подставим её в уравнение:
Используем своё право выбора u, взяв его
таким, чтобы выражение в скобках было равно нулю.
(*)
Слайд 14Найдём производную:
Подставим её в уравнение:
Используем своё право выбора u, взяв его
таким, чтобы выражение в скобках было равно нулю.
(**)
Слайд 30Найдем частное решение ДУ:
Подставим начальные условия в общее решение ДУ и
вычислим С:
- общее решение
или
частное решение
Слайд 31Пример 5. Найти общее решение ДУ:
Нужно привести к виду
Решение:
Иногда нужно решать
линейные ДУ относительно х: у принимаем за независимую переменную, а х- за искомую функцию.
