- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальное исчисление функций одной переменной презентация
Содержание
- 1. Дифференциальное исчисление функций одной переменной
- 2. Приращение функции и аргумента
- 3. Определение производной функции
- 4. Геометрический смысл производной функции
- 5. Правила дифференцирования функций
- 6. Производная сложной функции
- 7. Производные основных элементарных функций
- 8. Производные высших порядков
- 9. Понятие дифференциала функции
- 10. Найти дифференциал функции
- 11. Свойства дифференциала Дифференциал постоянной равен нулю: Cледствие:
Слайд 1
Дифференциальное исчисление функций одной переменной
Определение производной. Ее геометрический и физический
Связь между непрерывностью и дифференцируемостью функции. Необходимое условие существования производной.
Правило дифференциорания функций.
Производная сложной и обратной функции.
Производные основных элементарных функций.
Дифференцирование неявных и параметрически заданных функций.
Производные высших порядков.
Дифференциал функции. Свойства дифференциала.
Слайд 2
Приращение функции и аргумента
Пусть функция
промежутке X. Рассмотрим точку
Разность называется приращением аргумента x.
Разность называется приращением функции y=f(x) в точке x,
соответствующее приращению аргумента .
f(x)
Слайд 3
Определение производной функции
Определение
Производной функции y=f(x) в точке x называется
предел отношения приращения
приращению аргумента, когда приращение
аргумента стремится к нулю.
Обозначения производной:
Если функция y=f(x) в точке x имеет конечную производную, то
функция y=f(x) называется дифференцируемой в этой точке.
Функция, дифференцируемая во всех точках промежутка X,
называется дифференцируемой на этом промежутке.
Слайд 4
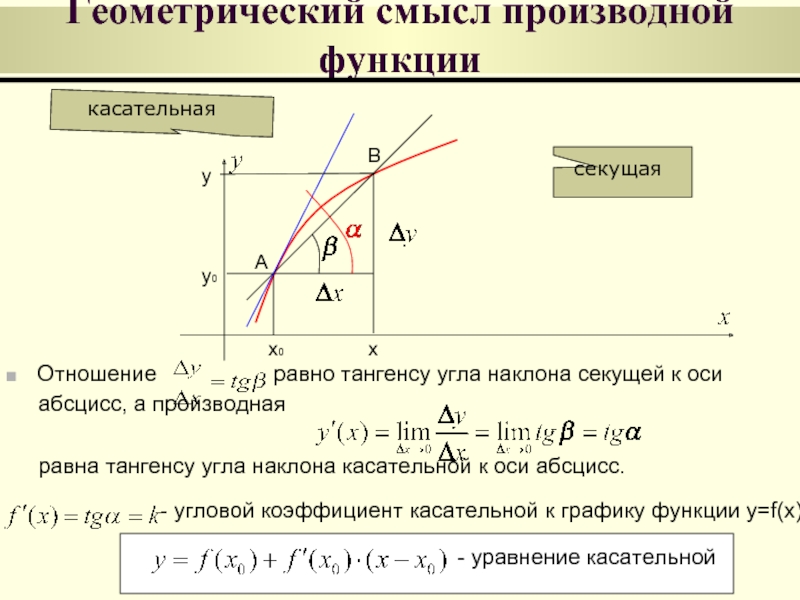
Геометрический смысл производной функции
Отношение
абсцисс, а производная
равна тангенсу угла наклона касательной к оси абсцисс.
касательная
секущая
x0
x
y0
y
B
A
- угловой коэффициент касательной к графику функции y=f(x)
- уравнение касательной
Слайд 5
Правила дифференцирования функций
Если функции
, то их сумма , произведение
и частное также имеют производные в
этой точке и справедливы формулы
Производная постоянной равна нулю:
Cледствие:
Слайд 6
Производная сложной функции
Если y=f(u) и u=h(x) дифференцируемые функции от
своих аргументов,
y=f(h(x)) существует и равна
или
Теорема
(о производной сложной функции)
Пример:
1.
2.
Слайд 8
Производные высших порядков
Обозначения производной второго порядка:
Если функция
Производные порядка выше первого называются производными высших порядков.
- производная первого порядка функции y=f(x)
- производная второго порядка функции y=f(x)
…………………………………….
- производная n-ого порядка функции y=f(x)
Слайд 9
Понятие дифференциала функции
Определение
Дифференциалом функции y=f(x) называется главная, линейная относительно
Обозначение:
Рассмотрим функцию y=x. Вычислим ее дифференциал:
dy – дифференциал первого порядка
Дифференциалом функции y=f(x) равен произведению производной этой функции на дифференциал независимой переменной