- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное решение систем нелинейных уравнений СНУ презентация
Содержание
- 1. Численное решение систем нелинейных уравнений СНУ
- 2. Общий вид СНУ где F –
- 3. Методы решения СНУ: 1. Прямых методов
- 4. Метод Зейделя (метод простых итераций) Ограниченный
- 5. Требование Функции Fi(x1, x2,…, xn) должны быть
- 6. Метод Зейделя на примере СНУ 3-го порядка
- 7. Получим новую систему:
- 8. 5. Далее рассчитывается разность между значениями
- 9. ЗАМЕЧАНИЕ Метод Зейделя применим, если
- 10. Примеры:
- 11. Метод Ньютона для решения СНУ
- 12. Для реализации метода Ньютона необходимо задать следующие
- 13. Требование Функции Fi(x1, x2,…, xn) должны быть
- 14. Метод Ньютона на примере СНУ 3-го порядка
- 15. F1, F2 и F3 разлагаются в ряд
- 16. Получим систему линейных алгебраических уравнений:
- 17. СЛАУ решается
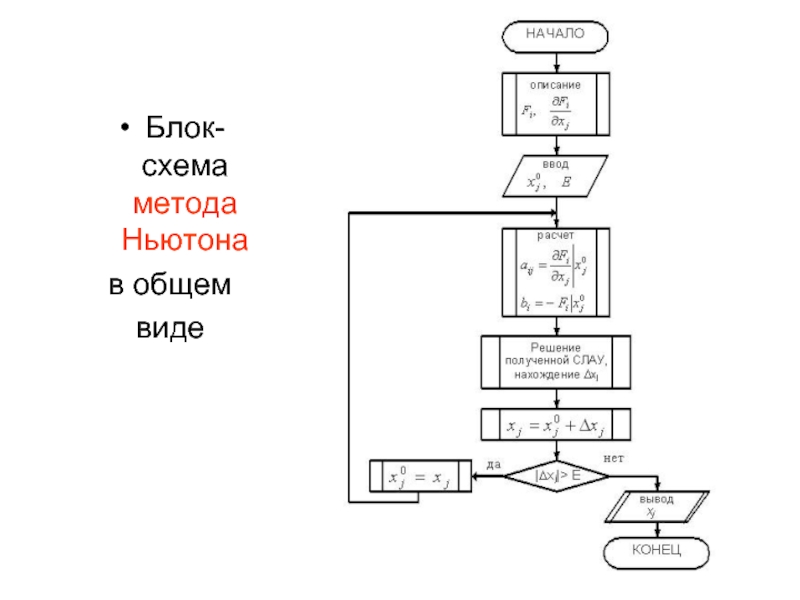
- 19. Блок-схема метода Ньютона в общем виде
- 20. Блок-схема метода Ньютона
- 21. Замечание Метод Ньютона является неустойчивым, прогнозировать
Общий вид СНУ где F – функции нескольких переменных, х – неизвестные n –порядок системы
Слайд 3Методы решения СНУ:
1. Прямых методов
для решения СНУ не существует.
2. Итерационные
методы.
Методы являются неустойчивыми, однако точность полученного решения определяется пользователем.
Методы являются неустойчивыми, однако точность полученного решения определяется пользователем.
Слайд 4Метод Зейделя
(метод простых итераций)
Ограниченный круг СНУ
Исходные данные:
Fi(x1, x2,…, xn)
Х(0)
Е
Слайд 5Требование
Функции Fi(x1, x2,…, xn) должны быть непрерывны в окрестности точки истинного
решения Х и точки начального приближения Х(0)
Слайд 6Метод Зейделя на примере СНУ 3-го порядка
Из 1-го уравнения выражаем неизвестное
х1.
Из 2-го уравнения выражаем неизвестное х2.
Из 3-го уравнения выражаем неизвестное х3.
Из 2-го уравнения выражаем неизвестное х2.
Из 3-го уравнения выражаем неизвестное х3.
Слайд 7Получим новую систему:
2. В правую часть 1-го уравнения подставляем начальные приближения
неизвестных х2(0) и х3(0). Получаем уточненное значение неизвестного х1(1).
3. В правую часть 2-го уравнения подставляем начальное приближение неизвестного х3(0) и уточненное значение х1(1). Получаем уточненное значение неизвестного х2(1).
4. В правую часть 3-го уравнения подставляем уточненные значения неизвестных х1(1) и х2(1). Получаем уточненное значение неизвестного х3(1).
3. В правую часть 2-го уравнения подставляем начальное приближение неизвестного х3(0) и уточненное значение х1(1). Получаем уточненное значение неизвестного х2(1).
4. В правую часть 3-го уравнения подставляем уточненные значения неизвестных х1(1) и х2(1). Получаем уточненное значение неизвестного х3(1).
Слайд 8
5. Далее рассчитывается разность между значениями начальных приближений и уточненными значениями
неизвестных.
Если то считается, что значения х1(1)., х2(1)., х3(1) являются решением данной системы. В противном случае эти значения принимаются за начальное приближение и процесс повторяется.
Если то считается, что значения х1(1)., х2(1)., х3(1) являются решением данной системы. В противном случае эти значения принимаются за начальное приближение и процесс повторяется.
Слайд 9
ЗАМЕЧАНИЕ
Метод Зейделя применим, если
неизвестные из соответствующих уравнений можно выразить в явном
виде.
Метод Зейделя для решения СНУ не является универсальным.
Метод Зейделя для решения СНУ не является универсальным.
Слайд 11Метод Ньютона
для решения СНУ
Основа: разложение функций в ряд Тейлора относительно
значений начальных приближений неизвестных.
Затем применяется линеаризация системы.
Затем применяется линеаризация системы.
Слайд 12Для реализации метода Ньютона необходимо задать следующие данные:
1. Выражения для функций
F1, F2 ,…, Fn в аналитическом виде.
2. Выражения для частных производных функций F1, F2 ,…, Fn по каждому аргументу в аналитическом виде.
3. x10, x20,…, xn0.
4. Е.
2. Выражения для частных производных функций F1, F2 ,…, Fn по каждому аргументу в аналитическом виде.
3. x10, x20,…, xn0.
4. Е.
Слайд 13Требование
Функции Fi(x1, x2,…, xn) должны быть непрерывны и дифференцируемы в окрестности
точки истинного решения Х и точки начального приближения Х(0)
Слайд 14Метод Ньютона на примере СНУ 3-го порядка
Задано: x10, x20 и x30.
Истинное
решение системы: x1, x2 и x3.
Разность:
Δx1=x1-x10, Δx2=x2-x20, Δx3=x3-x30
Разность:
Δx1=x1-x10, Δx2=x2-x20, Δx3=x3-x30
Слайд 15F1, F2 и F3 разлагаются в ряд Тейлора. Члены, содержащие производные старше
первого порядка отбрасываются.
Преобразуем систему.
Слайд 16Получим систему линейных алгебраических уравнений:
Неизвестные - Δx1, Δx2 и Δx3,
Вектор-столбец
свободных членов – F1, F2 и F3 в точке начального приближения,
Коэффициенты - производные функций F1, F2 и F3 по неизвестным x1, x2 и x3 в точке начального приближения.
Коэффициенты - производные функций F1, F2 и F3 по неизвестным x1, x2 и x3 в точке начального приближения.
Слайд 17
СЛАУ решается любым известным методом (метод Гаусса, метод Крамера), получаем значения
неизвестных Δx1, Δx2 и Δx3
x1, x2 и x3 рассчитываются по формулам:
x1=x10+Δx1, x2=x20+Δx2, x3=x30+Δx3
x1, x2 и x3 рассчитываются по формулам:
x1=x10+Δx1, x2=x20+Δx2, x3=x30+Δx3
Матрица Якоби
(Якобиан)
Слайд 18
Если полученные значения Δx1 и Δx2 и Δx3 по модулю оказались
менее заданной точности Е, то считается, что рассчитанные значения x1, x2 и x3 являются решением данной системы нелинейных уравнений.
Если хотя бы одно из значений Δx1, Δx2, Δx3 по модулю оказалось выше заданной точности Е, то рассчитанные значения x1, x2 и x3 принимаются в качестве нового начального приближения и процесс повторяется.
Если хотя бы одно из значений Δx1, Δx2, Δx3 по модулю оказалось выше заданной точности Е, то рассчитанные значения x1, x2 и x3 принимаются в качестве нового начального приближения и процесс повторяется.
Слайд 21Замечание
Метод Ньютона является неустойчивым, прогнозировать сходимость невозможно.
Сходимость метода зависит от порядка
системы и от удачного выбора начального приближения решения.
