- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 05. Основные понятия проективной геометрии презентация
Содержание
- 1. Лекция 05. Основные понятия проективной геометрии
- 2. 1. Понятие группы преобразований
- 3. Умножение преобразований Некоторые преобразования можно составить из нескольких других.
- 4. Умножение преобразований Некоторые преобразования можно составить
- 5. Умножение преобразований Некоторые преобразования можно составить
- 6. Пусть есть некоторая совокупность преобразований с операцией умножения. Она обладает такими свойствами:
- 7. Пусть есть некоторая совокупность преобразований с операцией
- 8. Пусть есть некоторая совокупность преобразований с операцией
- 9. Пусть есть некоторая совокупность преобразований с операцией
- 10. Пусть есть некоторая совокупность преобразований с операцией
- 11. Таким образом, всякая совокупность взаимно однозначных преобразований
- 12. Таким образом, всякая совокупность взаимно однозначных преобразований
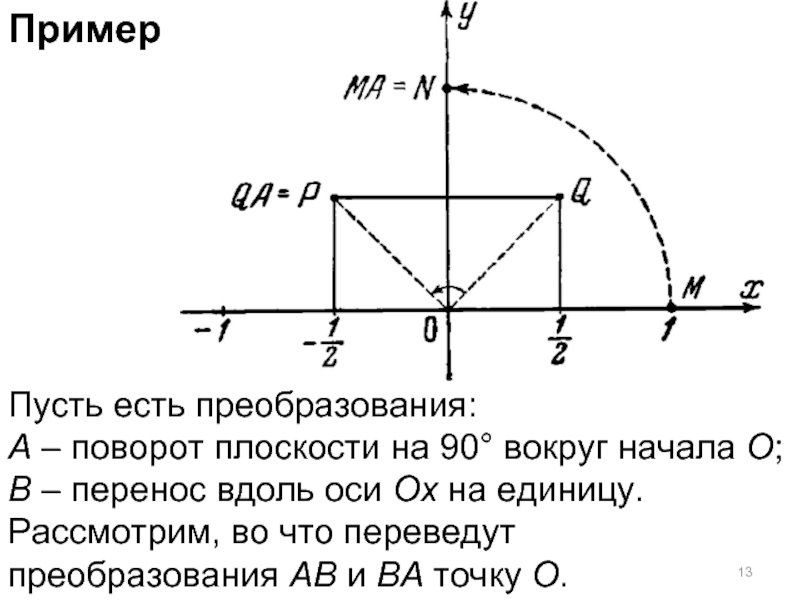
- 13. Пример Пусть есть преобразования: А – поворот
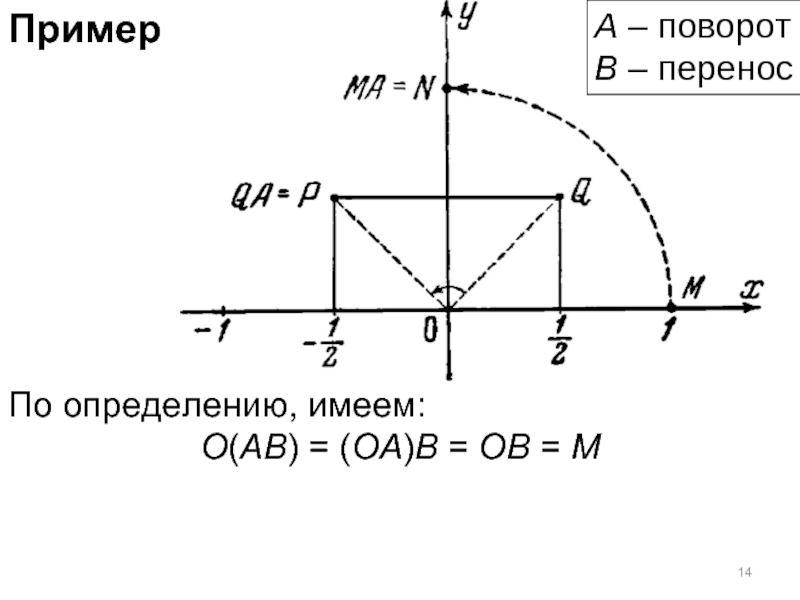
- 14. Пример По определению, имеем: O(AB) = (OA)B
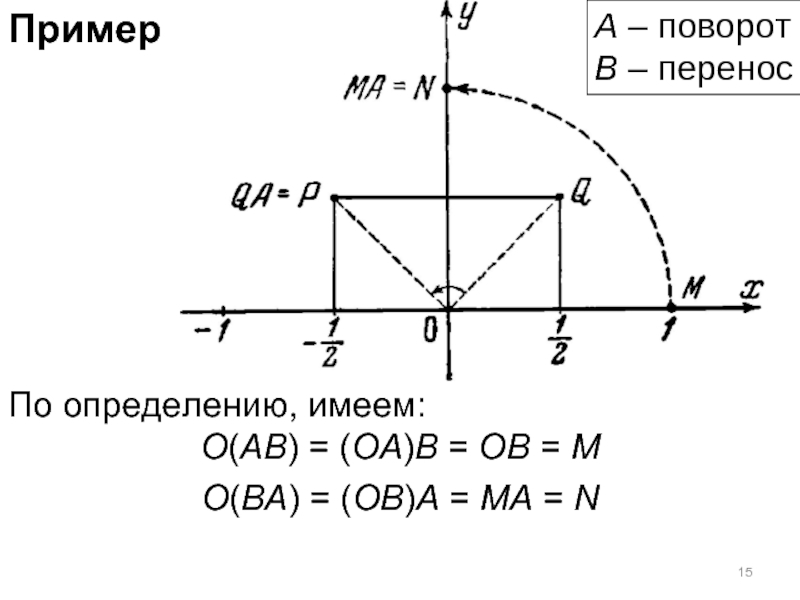
- 15. Пример По определению, имеем: O(AB) = (OA)B
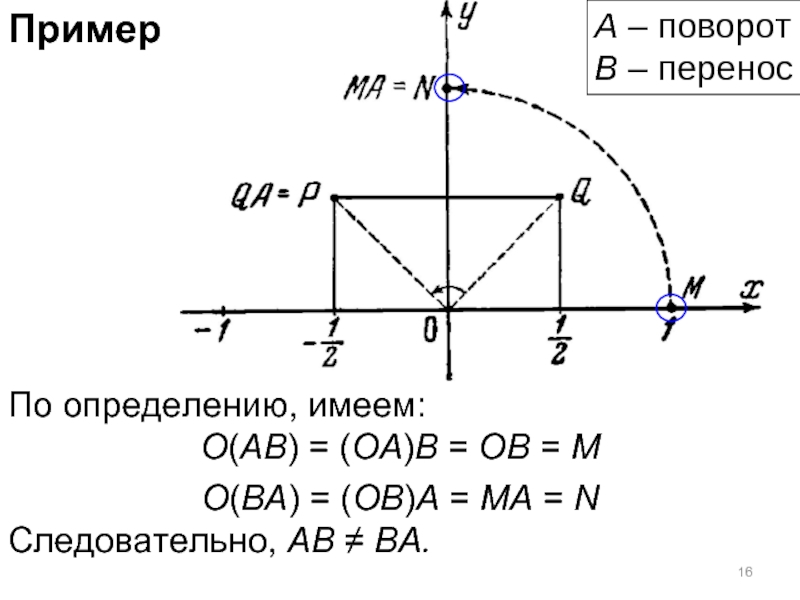
- 16. Пример По определению, имеем: O(AB) = (OA)B
- 17. Пример Выясним геометрическую природу ВА. Рассмотрим точку
- 18. Пример Выясним геометрическую природу ВА. Рассмотрим точку
- 19. Пример Аналогично исследуем АВ. Рассмотрим точку Q.
- 20. Пример Аналогично исследуем АВ. Рассмотрим точку Q.
- 21. 2. Группа проективных преобразований
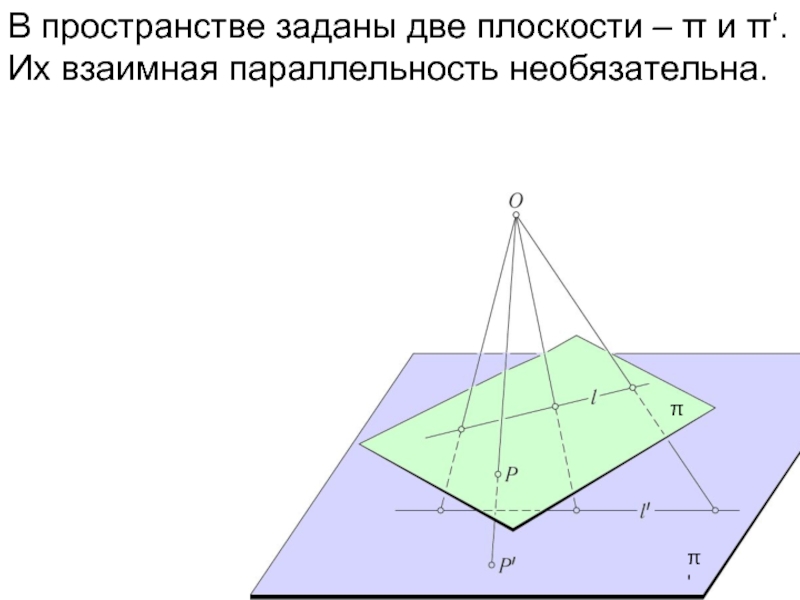
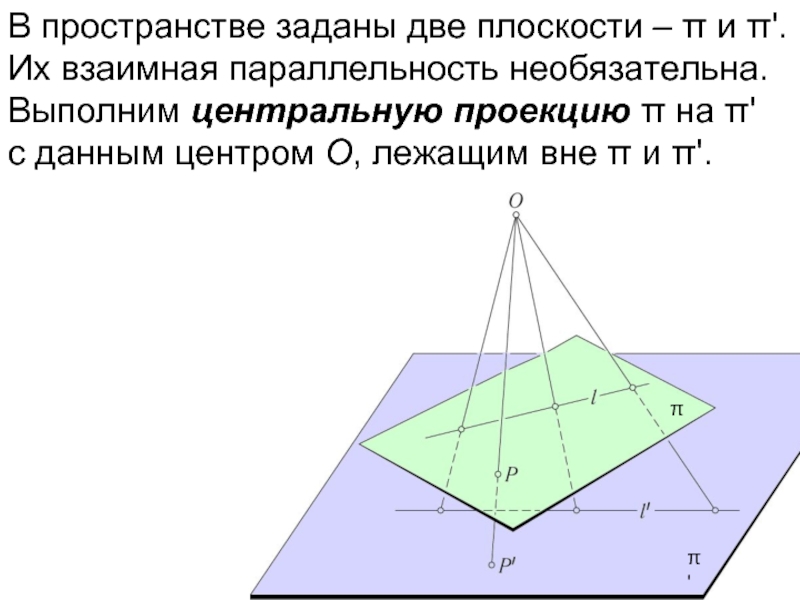
- 22. В пространстве заданы две плоскости – π
- 23. В пространстве заданы две плоскости – π
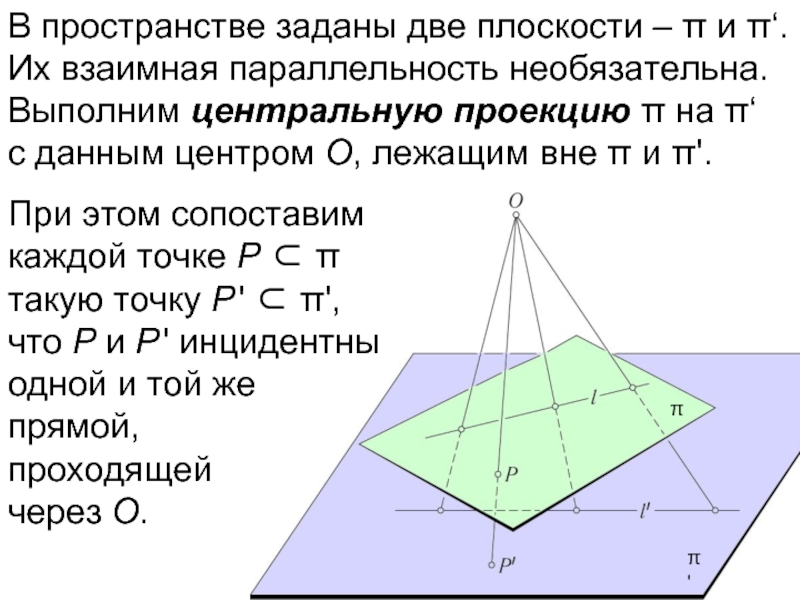
- 24. В пространстве заданы две плоскости – π
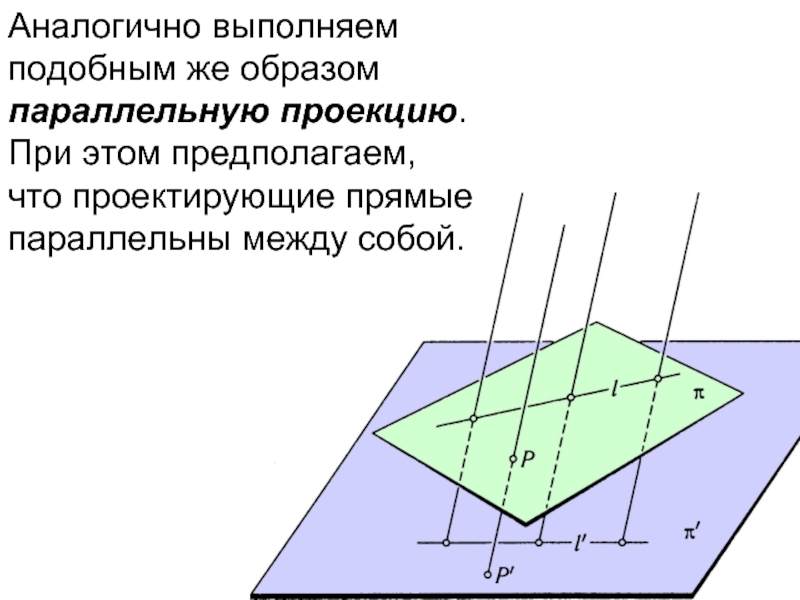
- 25. Аналогично выполняем подобным же образом параллельную проекцию.
- 26. Точно так же определяется проекция прямой или
- 27. Всякое отображение одной фигуры на другую,
- 28. Замечание Если две фигуры связаны только одним проектированием, то говорят, что они перспективны.
- 29. Замечание Если две фигуры связаны только одним
- 30. Замечание Если две фигуры связаны только одним
- 31. Проективная геометрия плоскости или прямой составляется из
- 32. Проективной геометрии противопоставляется метрическая геометрия, которая понимается
- 33. Cформулируем некоторые проективные свойства.
- 34. Точка проектируется в точку.
- 35. Точка проектируется в точку. Прямая линия проектируется в прямую.
- 36. Точка проектируется в точку. Прямая линия
- 37. π π' Точка проектируется в точку.
- 38. Если точка A и прямая l
- 39. Если точка A и прямая l
- 40. Следствия.
- 41. Если три точки (или более) коллинеарны,
- 42. Если три точки (или более) коллинеарны,
- 43. Если три точки (или более) коллинеарны,
- 44. Итак, инцидентность, коллинеарность, конкуррентность
- 45. Итак, инцидентность, коллинеарность, конкуррентность
- 46. Пример
- 47. Равнобедренные или равносторонние треугольники могут
- 48. Равнобедренные или равносторонние треугольники могут
1. Понятие
группы
преобразований
Слайд 4Умножение преобразований
Некоторые преобразования можно составить из нескольких других.
Пример. Винтовые движения составляются
из поворотов вокруг оси и сдвигов вдоль оси.
Слайд 5Умножение преобразований
Некоторые преобразования можно составить из нескольких других.
Пример. Винтовые движения составляются
из поворотов вокруг оси и сдвигов вдоль оси.
Процесс составления новых преобразований из заданных и есть
умножение преобразований.
Процесс составления новых преобразований из заданных и есть
умножение преобразований.
Слайд 6Пусть есть некоторая совокупность преобразований с операцией умножения.
Она обладает такими свойствами:
Слайд 7Пусть есть некоторая совокупность преобразований с операцией умножения.
Она обладает такими свойствами:
1.
Произведение двух преобразований, принадлежащих совокупности, само принадлежит этой совокупности.
Слайд 8Пусть есть некоторая совокупность преобразований с операцией умножения.
Она обладает такими свойствами:
1.
Произведение двух преобразований, принадлежащих совокупности, само принадлежит этой совокупности.
2. Произведение преобразований ассоциативно.
2. Произведение преобразований ассоциативно.
Слайд 9Пусть есть некоторая совокупность преобразований с операцией умножения.
Она обладает такими свойствами:
1.
Произведение двух преобразований, принадлежащих совокупности, само принадлежит этой совокупности.
2. Произведение преобразований ассоциативно.
3. Тождественное преобразование принадлежит совокупности.
2. Произведение преобразований ассоциативно.
3. Тождественное преобразование принадлежит совокупности.
Слайд 10Пусть есть некоторая совокупность преобразований с операцией умножения.
Она обладает такими свойствами:
1.
Произведение двух преобразований, принадлежащих совокупности, само принадлежит этой совокупности.
2. Произведение преобразований ассоциативно.
3. Тождественное преобразование принадлежит совокупности.
4. Если преобразование принадлежит совокупности, то обратное преобразование также принадлежит этой совокупности.
2. Произведение преобразований ассоциативно.
3. Тождественное преобразование принадлежит совокупности.
4. Если преобразование принадлежит совокупности, то обратное преобразование также принадлежит этой совокупности.
Слайд 11Таким образом, всякая совокупность взаимно однозначных преобразований множества М, обладающая этими свойствами, называется группой преобразований множества
М.
Слайд 12Таким образом, всякая совокупность взаимно однозначных преобразований множества М, обладающая этими свойствами, называется группой преобразований множества
М.
Группа преобразований не обязательно коммутативна.
То есть, группа преобразований может не быть абелевой.
Группа преобразований не обязательно коммутативна.
То есть, группа преобразований может не быть абелевой.
Слайд 13Пример
Пусть есть преобразования:
А – поворот плоскости на 90° вокруг начала О;
В – перенос вдоль оси Ох на единицу.
Рассмотрим, во что переведут преобразования АВ и ВА точку О.
Рассмотрим, во что переведут преобразования АВ и ВА точку О.
Слайд 15Пример
По определению, имеем:
O(AB) = (OA)B = OB = M
O(BA) = (OB)A
= MA = N
А – поворот
В – перенос
Слайд 16Пример
По определению, имеем:
O(AB) = (OA)B = OB = M
O(BA) = (OB)A
= MA = N
Следовательно, AB ≠ BA.
Следовательно, AB ≠ BA.
А – поворот
В – перенос
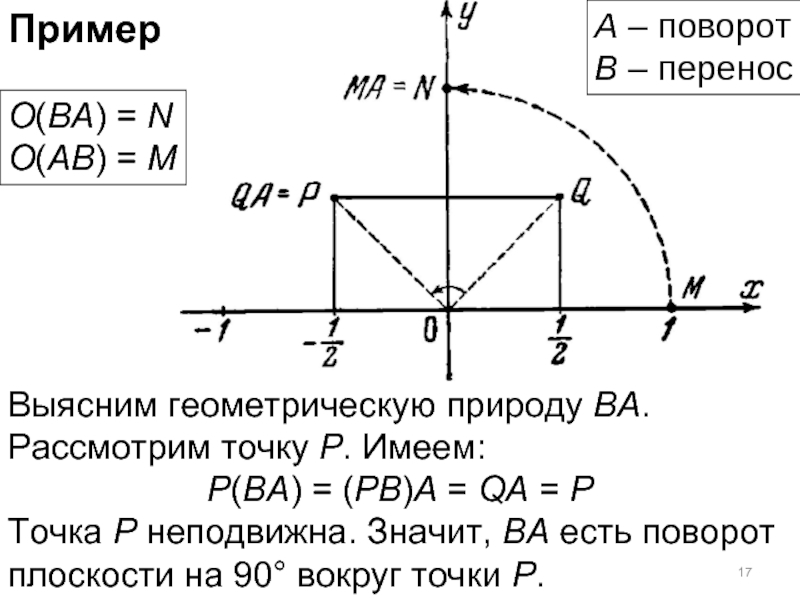
Слайд 17Пример
Выясним геометрическую природу ВА. Рассмотрим точку Р. Имеем:
P(BA) = (PB)A =
QA = P
Точка Р неподвижна. Значит, ВА есть поворот плоскости на 90° вокруг точки Р.
Точка Р неподвижна. Значит, ВА есть поворот плоскости на 90° вокруг точки Р.
А – поворот
В – перенос
O(BA) = N
O(AB) = M
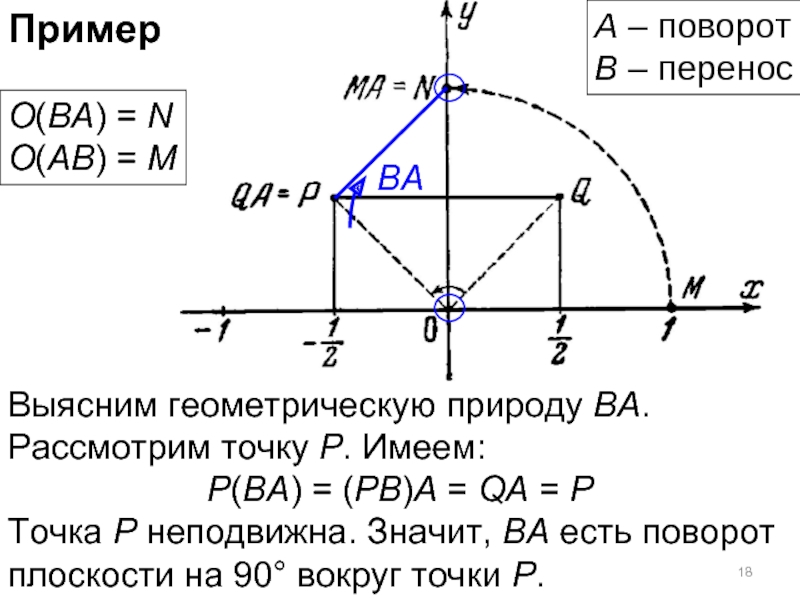
Слайд 18Пример
Выясним геометрическую природу ВА. Рассмотрим точку Р. Имеем:
P(BA) = (PB)A =
QA = P
Точка Р неподвижна. Значит, ВА есть поворот плоскости на 90° вокруг точки Р.
Точка Р неподвижна. Значит, ВА есть поворот плоскости на 90° вокруг точки Р.
А – поворот
В – перенос
O(BA) = N
O(AB) = M
BA
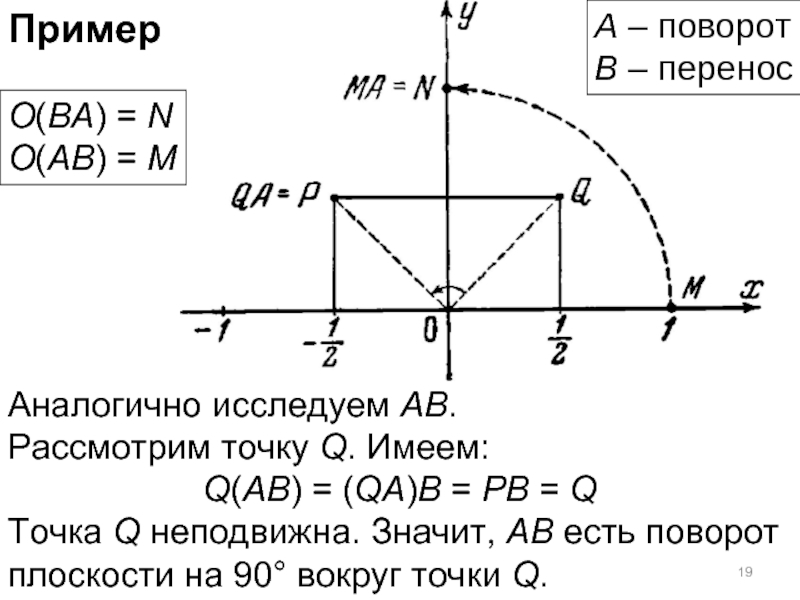
Слайд 19Пример
Аналогично исследуем АВ.
Рассмотрим точку Q. Имеем:
Q(AB) = (QA)B = PB =
Q
Точка Q неподвижна. Значит, АB есть поворот плоскости на 90° вокруг точки Q.
Точка Q неподвижна. Значит, АB есть поворот плоскости на 90° вокруг точки Q.
А – поворот
В – перенос
O(BA) = N
O(AB) = M
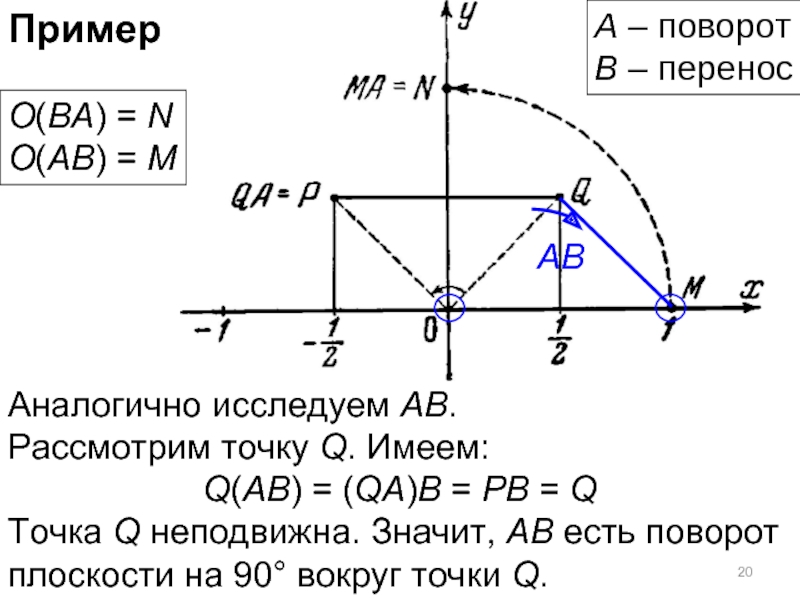
Слайд 20Пример
Аналогично исследуем АВ.
Рассмотрим точку Q. Имеем:
Q(AB) = (QA)B = PB =
Q
Точка Q неподвижна. Значит, АB есть поворот плоскости на 90° вокруг точки Q.
Точка Q неподвижна. Значит, АB есть поворот плоскости на 90° вокруг точки Q.
А – поворот
В – перенос
O(BA) = N
O(AB) = M
AB
Слайд 23В пространстве заданы две плоскости – π и π'. Их взаимная
параллельность необязательна. Выполним центральную проекцию π на π'
с данным центром O, лежащим вне π и π'.
π
π'
Слайд 24В пространстве заданы две плоскости – π и π‘. Их взаимная
параллельность необязательна. Выполним центральную проекцию π на π‘
с данным центром O, лежащим вне π и π'.
При этом сопоставим каждой точке P ⊂ π такую точку P ' ⊂ π', что P и P ' инцидентны одной и той же прямой, проходящей через O.
При этом сопоставим каждой точке P ⊂ π такую точку P ' ⊂ π', что P и P ' инцидентны одной и той же прямой, проходящей через O.
π
π'
Слайд 25Аналогично выполняем
подобным же образом
параллельную проекцию.
При этом предполагаем,
что проектирующие прямые
параллельны между собой.
Слайд 26Точно так же определяется проекция прямой или кривой линии l в плоскости π
на некоторую линию l'
в плоскости π'.
Причём и в этом случае проекция
может быть
центральной или параллельной.
Слайд 27Всякое отображение одной фигуры на другую, которое получается посредством проектирования (центрального или параллельного) или же
посредством
конечной последовательности
таких проектирований,
называется
проективным преобразованием.
Слайд 28Замечание
Если две фигуры связаны только одним проектированием, то говорят,
что они перспективны.
Слайд 29Замечание
Если две фигуры связаны только одним проектированием, то говорят,
что они перспективны.
Таким
образом, если фигура F
в результате проективного преобразования переходит в фигуру F', то это значит,
что или фигуры F и F ' перспективны,
Слайд 30Замечание
Если две фигуры связаны только одним проектированием, то говорят,
что они перспективны.
Таким
образом, если фигура F
в результате проективного преобразования переходит в фигуру F', то это значит,
что или фигуры F и F ' перспективны,
или же можно указать последовательность таких фигур F, F1, F2, ..., Fn, F ',
что любые две рядом стоящие в ней фигуры перспективны.
Слайд 31Проективная геометрия плоскости или прямой составляется из системы геометрических теорем, сохраняющихся при произвольных проективных преобразованиях
соответствующих фигур.
Слайд 32Проективной геометрии противопоставляется метрическая геометрия, которая понимается как система теорем, устанавливающих связи между величинами в рассматриваемых фигурах, инвариантные только относительно класса
движений.
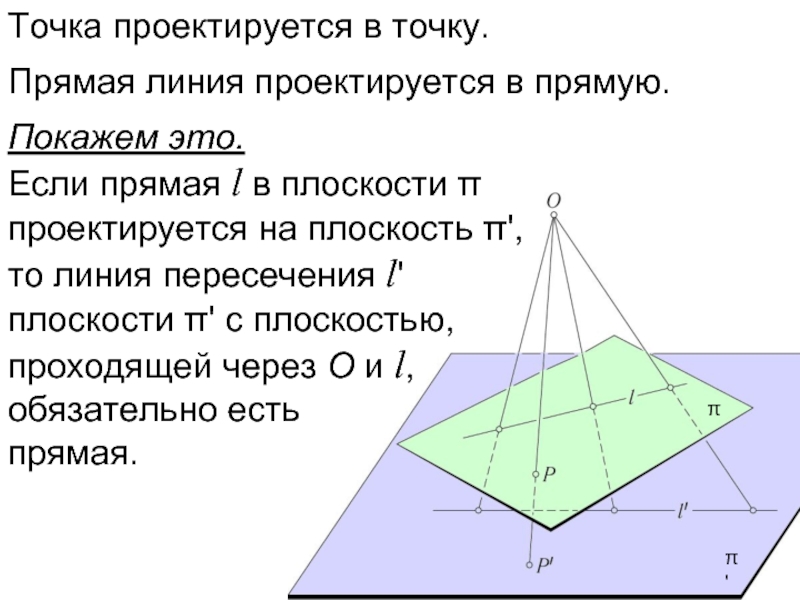
Слайд 37π
π'
Точка проектируется в точку.
Прямая линия проектируется в прямую.
Покажем это.
Если прямая l
в плоскости π
проектируется на плоскость π',
то линия пересечения l'
плоскости π' с плоскостью,
проходящей через O и l,
обязательно есть
прямая.
Слайд 38Если точка A и прямая l инцидентны, то точка A' и
прямая l',
возникающие из них
при проективном преобразовании,
также инцидентны.
Слайд 39Если точка A и прямая l инцидентны, то точка A' и
прямая l',
возникающие из них
при проективном преобразовании,
также инцидентны.
Другими словами, инцидентность точки и прямой есть свойство, инвариантное относительно группы проективных преобразований.
Другими словами, инцидентность точки и прямой есть свойство, инвариантное относительно группы проективных преобразований.
Слайд 41Если три точки (или более) коллинеарны, т.е. инцидентны с одной и
той же прямой,
то их отображения также коллинеарны.
Слайд 42Если три точки (или более) коллинеарны, т.е. инцидентны с одной и
той же прямой,
то их отображения также коллинеарны.
Если в плоскости π три прямые (или более) конкуррентны, т.е. инцидентны с одной и той же точкой, то их отображения – также конкуррентные прямые.
Если в плоскости π три прямые (или более) конкуррентны, т.е. инцидентны с одной и той же точкой, то их отображения – также конкуррентные прямые.
Слайд 43Если три точки (или более) коллинеарны, т.е. инцидентны с одной и
той же прямой,
то их отображения также коллинеарны.
Если в плоскости π три прямые (или более) конкуррентны, т.е. инцидентны с одной и той же точкой, то их отображения – также конкуррентные прямые.
Если в плоскости π три прямые (или более) конкуррентны, т.е. инцидентны с одной и той же точкой, то их отображения – также конкуррентные прямые.
concurrere (лат.) – бежать вместе
Слайд 44Итак,
инцидентность,
коллинеарность,
конкуррентность
являются проективными свойствами
(инвариантными относительно
проективных преобразований).
Слайд 45Итак,
инцидентность,
коллинеарность,
конкуррентность
являются проективными свойствами
(инвариантными относительно
проективных преобразований).
Величины отрезков
и углов,
а также отношения этих величин
в общем случае
изменяются при проектировании.
Слайд 47 Равнобедренные или равносторонние треугольники могут спроектироваться на треугольники с тремя
различными сторонами.
Слайд 48 Равнобедренные или равносторонние треугольники могут спроектироваться на треугольники с тремя
различными сторонами.
Следовательно, хотя понятие «треугольник» и принадлежит
проективной геометрии, понятие «равносторонний треугольник» ей не принадлежит, а принадлежит только метрической геометрии.
Следовательно, хотя понятие «треугольник» и принадлежит
проективной геометрии, понятие «равносторонний треугольник» ей не принадлежит, а принадлежит только метрической геометрии.
