- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное решение обыкновенных дифференциальных уравнений презентация
Содержание
- 1. Численное решение обыкновенных дифференциальных уравнений
- 2. Все дифференциальные уравнения делятся на 2 большие
- 3. Обыкновенные дифференциальные уравнения : Общий
- 4. Общее решение ОДУ - бесконечное множество функций
- 5. Численные методы решения ОДУ классифицируются следующим образом:
- 6. Также численные методы решения ОДУ характеризуются следующими
- 7. Решение ОДУ 1-го порядка Общий
- 8. Метод Эйлера y’=f(x, y)
- 9. Графическая интерпретация метода Эйлера Предположим,
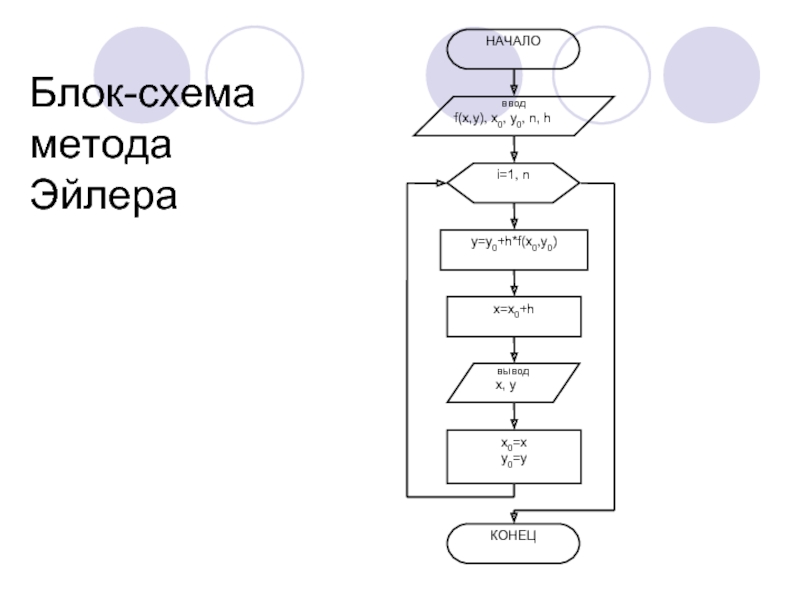
- 10. Блок-схема метода Эйлера
- 11. Характеристика метода Эйлера Метод
- 12. Метод Эйлера-Коши Данный метод является
- 13. Таким образом, формула для решения
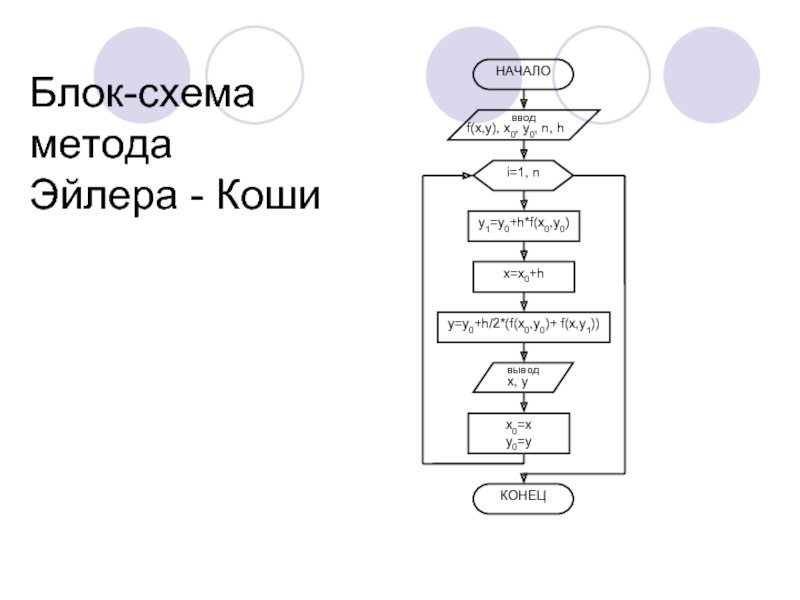
- 14. Блок-схема метода Эйлера - Коши
- 15. Метод Рунге-Кутта 4 порядка Данный
- 16. Блок-схема метода Рунге-Кутта 4 порядка
- 17. Метод Адамса Многошаговый метод (4-шаговый)
- 18. Решение систем обыкновенных дифференциальных уравнений Рассмотрим систему
- 19. Данную систему можно решить любым методом, применимым
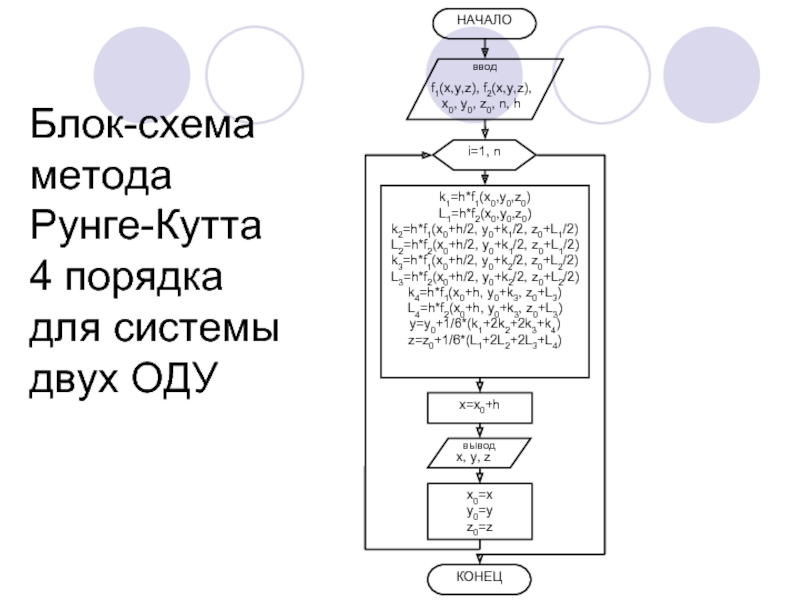
- 20. Метод Рунге-Кутта 4-го порядка:
- 21. Блок-схема метода Рунге-Кутта 4 порядка для системы двух ОДУ
- 22. Решение обыкновенных дифференциальных уравнений высших порядков Любое
- 23. Пример решения ОДУ 2-го порядка:
Слайд 2Все дифференциальные уравнения делятся на 2 большие категории:
1. В ДУ
2. В ДУ входит функция нескольких независимых переменных.
Слайд 3Обыкновенные дифференциальные уравнения :
Общий вид ОДУ:
F(x, y, y’, y’’,…,y(n))=0
Наивысший порядок
ОДУ часто представляют в виде:
y(n)=f(x, y, y’, y’’,…,y(n-1))
уравнение, разрешенное относительно старшей производной.
Слайд 4Общее решение ОДУ - бесконечное множество функций в аналитическом виде.
Точное решение
Для нахождения точного решения необходимо задать дополнительные условия (например, начальную точку). Получаем задачу Коши или краевую задачу.
При использовании численных методов решения ОДУ решение представляет собой набор точек, которые лежат на кривой истинного решения или расположены вблизи нее (ввиду погрешности метода).
Слайд 5Численные методы решения ОДУ классифицируются следующим образом:
1. ОДНОШАГОВЫЕ и МНОГОШАГОВЫЕ.
2. ЯВНЫЕ
Слайд 6Также численные методы решения ОДУ характеризуются следующими показателями:
Точность
Устойчивость
Точность – погрешность, с
Устойчивость метода характеризует возможность вообще получить достоверный результат.
Слайд 7Решение ОДУ 1-го порядка
Общий вид ОДУ 1-го порядка:
F(x, y, y’)=0
Уравнение
y’=f(x, y)
Начальная точка: x0, y0.
Количество точек на интегральной кривой решения n
Шаг h, с которым будет изменяться значение аргумента.
Слайд 8Метод Эйлера
y’=f(x, y)
Представляем производную функции y’ в виде конечной
За величину приращения аргумента Δx принимается величина шага h:
Тогда:
Аналогично:
В общем виде: - формула Эйлера
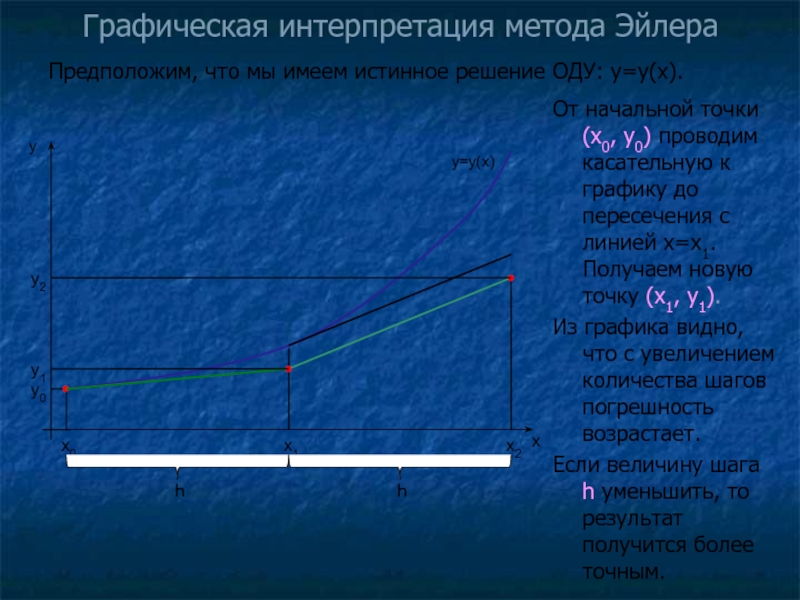
Слайд 9Графическая интерпретация метода Эйлера
Предположим, что мы имеем истинное решение ОДУ:
От начальной точки (x0, y0) проводим касательную к графику до пересечения с линией x=x1. Получаем новую точку (x1, y1).
Из графика видно, что с увеличением количества шагов погрешность возрастает.
Если величину шага h уменьшить, то результат получится более точным.
Слайд 11Характеристика метода Эйлера
Метод Эйлера является одношаговым методом, то есть для
Данный метод использует явную схему. В правой части формулы Эйлера стоят все известные величины.
Метод Эйлера не является устойчивым методом, поэтому он применяется только для ОДУ, решением которых являются достаточно гладкие функции.
Этот метод характеризуется первым порядком точности (точность низкая).
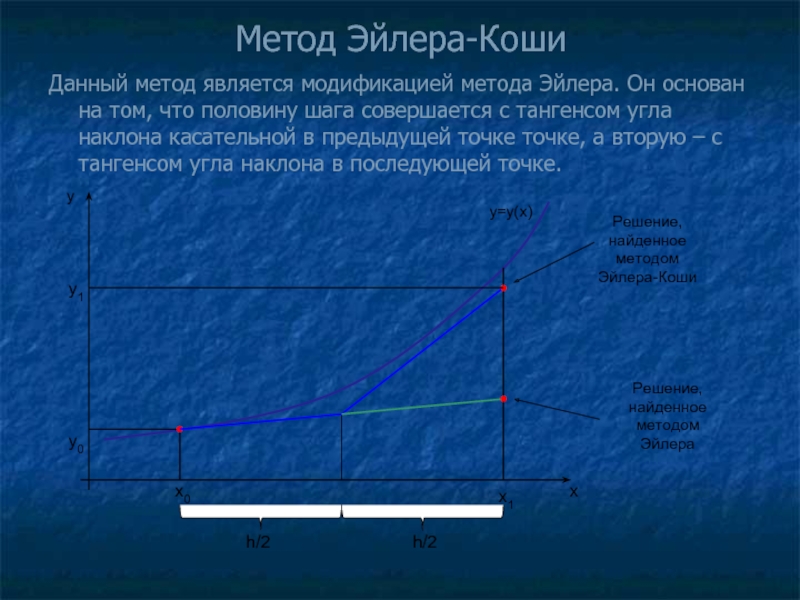
Слайд 12Метод Эйлера-Коши
Данный метод является модификацией метода Эйлера. Он основан на
Слайд 13
Таким образом, формула для решения ОДУ методом Эйлера-Коши будет следующей:
-
В левой и в правой части формулы Эйлера-Коши стоит неизвестная искомая величина yi+1 - метод является неявным.
Для его реализации находится приближенное значение yi+1 методом Эйлера, подставляется в правую часть формулы Эйлера-Коши и находится уточненное значение yi+1.
Метод является одношаговым, устойчивым, 2-го порядка точности (более точным, по сравнению с методом Эйлера)
Слайд 15Метод Рунге-Кутта 4 порядка
Данный метод 4-й порядок точности, является одношаговым,
Для реализации этого метода используются достаточно громоздкие формулы Рунге-Кутта:
Несмотря на сложные
формулы, данный метод
является самым
распространенным.
Слайд 17Метод Адамса
Многошаговый метод (4-шаговый)
Для расчета последующей точки необходимо знать
Как правило в задачах обычно известна только одна начальная точка. Поэтому три последующие точки вычисляются с использованием одношаговых методов, а затем используется 4-шаговый метод Адамса.
Данный метод имеет 4-й порядок точности, явную схему, но не всегда устойчив.
Слайд 18Решение систем обыкновенных дифференциальных уравнений
Рассмотрим систему из двух дифференциальных уравнений 1-го
Оба уравнения необходимо разрешить относительно старшей производной:
Пусть заданы начальные условия: x0, y0, z0.
Слайд 19Данную систему можно решить любым методом, применимым для решения единичных ОДУ.
Метод
Метод Эйлера-Коши:
Слайд 22Решение обыкновенных дифференциальных уравнений высших порядков
Любое дифференциальное уравнение высшего порядка можно
Рассмотрим дифференциальное уравнение 2-го порядка:
Заданы начальные условия: x0, y0, y’0
Разрешим уравнение относительно старшей производной:
Заменим первую производную y’ функцией z. Тогда y’’=z’, а y’0= z0 Получим систему:
Решаем полученную систему известными методами.