вероятностей.
4. Формула полной вероятности. Формула Байеса.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоремы сложения и умножения вероятностей. (Лекция 3) презентация
Содержание
- 1. Теоремы сложения и умножения вероятностей. (Лекция 3)
- 2. 09/03/2019 Ирина Юрьевна Харламова 1. УСЛОВНАЯ ВЕРОЯТНОСТЬ
- 3. 09/03/2019 Ирина Юрьевна Харламова Условная вероятность Вероятность
- 4. 09/03/2019 Ирина Юрьевна Харламова Условная вероятность
- 5. 09/03/2019 Ирина Юрьевна Харламова Условная
- 6. События А и В называются независимыми
- 7. 09/03/2019 Ирина Юрьевна Харламова 2. ПРОИЗВЕДЕНИЕ ВЕРОЯТНОСТЕЙ
- 8. ТЕОРЕМА 1 Вероятность совместного появления двух событий
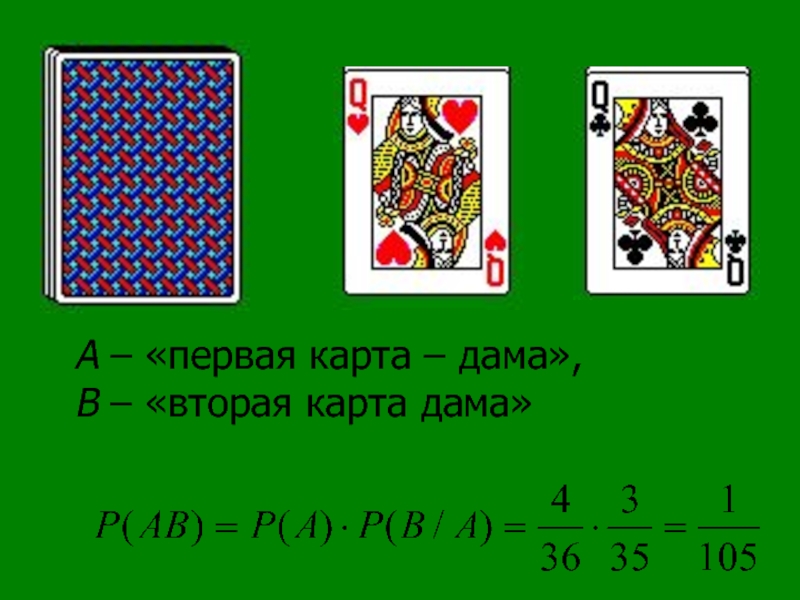
- 9. 09/03/2019 Ирина Юрьевна Харламова А – «первая
- 10. ТЕОРЕМА 2 Вероятность совместного появления двух независимых событий равна произведению их вероятностей, т.е.
- 11. 09/03/2019 Ирина Юрьевна Харламова ТЕОРЕМА 2 Усложненное
- 12. ТЕОРЕМА 3 Если для двух событий выполняется
- 13. ТЕОРЕМА 4 Вероятность совместного наступления конечного числа
- 14. 09/03/2019 Ирина Юрьевна Харламова Ю Р И
- 15. 09/03/2019 Ирина Юрьевна Харламова Ю Р И С Т
- 16. ТЕОРЕМА 5 Вероятность совместного появления нескольких событий,
- 17. 09/03/2019 Ирина Юрьевна Харламова Ю Р И С Т
- 18. 09/03/2019 Ирина Юрьевна Харламова 3. СУММА ВЕРОЯТНОСТЕЙ
- 19. ТЕОРЕМА 6 Вероятность появления одного из двух
- 20. 09/03/2019 Ирина Юрьевна Харламова 25 ЧЕЛОВЕК ИМЕЮТ
- 21. 09/03/2019 Ирина Юрьевна Харламова Какова вероятность того, что наугад вызванный курсант отличник или хорошист?
- 22. 09/03/2019 Ирина Юрьевна Харламова А – наугад вызванный
- 23. ТЕОРЕМА 7 Вероятность появления одного из нескольких
- 24. СЛЕДСТВИЕ Сумма вероятностей попарно несовместных событий, образующих полную группу, равна 1:
- 25. 09/03/2019 Ирина Юрьевна Харламова Два стрелка стреляют
- 26. 09/03/2019 Ирина Юрьевна Харламова А1 – поражение цели
- 27. ТЕОРЕМА 8 Вероятность появления хотя бы одного
- 28. 09/03/2019 Ирина Юрьевна Харламова
- 29. СЛЕДСТВИЕ В случае трех совместных событий вероятность
- 30. ТЕОРЕМА 9 Вероятность появления хотя бы одного
- 31. 09/03/2019 Ирина Юрьевна Харламова
- 32. 09/03/2019 Ирина Юрьевна Харламова 3. Формула полной вероятности. Формула Байеса
- 33. ТЕОРЕМА 10 Вероятность события А, которое может
- 34. 09/03/2019 Ирина Юрьевна Харламова Вероятность того, что
- 35. 09/03/2019 Ирина Юрьевна Харламова Обозначим через А
- 36. Алгоритм применения ф.Байеса 1. Выдвигают предположения – гипотезы
- 37. Алгоритм применения ф.Байеса 2. Устанавливают доопытные (априорные) вероятности
- 38. Алгоритм применения ф.Байеса 3. Проводят эксперимент, в результате
- 39. Алгоритм применения ф.Байеса где Р(А) определяется по
- 40. 09/03/2019 Ирина Юрьевна Харламова Вероятность обнаружить признак
- 41. 09/03/2019 Ирина Юрьевна Харламова А – в
- 42. 09/03/2019 Ирина Юрьевна Харламова А – в
- 43. Спасибо за внимание!
09/03/2019 Ирина Юрьевна Харламова 1. УСЛОВНАЯ
ВЕРОЯТНОСТЬ
Слайд 1Теоремы сложения и умножения вероятностей
1. Условная вероятность.
2. Теоремы умножения вероятностей.
3. Теоремы сложения
Слайд 309/03/2019
Ирина Юрьевна Харламова
Условная вероятность
Вероятность события А при условии, что событие В
с вероятностью Р(В)≠0 уже произошло, обозначается Р(А/В) и называется условной вероятностью события А при условии, что имело место событие В.
Слайд 409/03/2019
Ирина Юрьевна Харламова
Условная вероятность
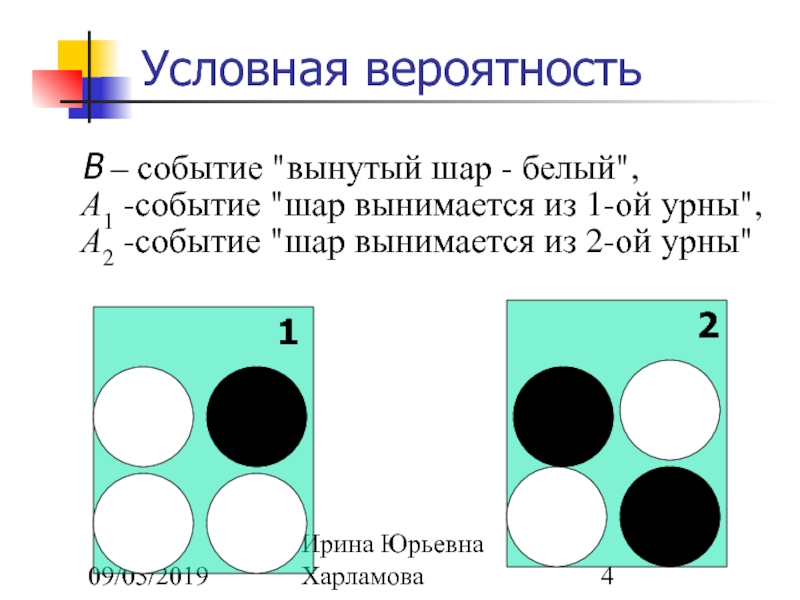
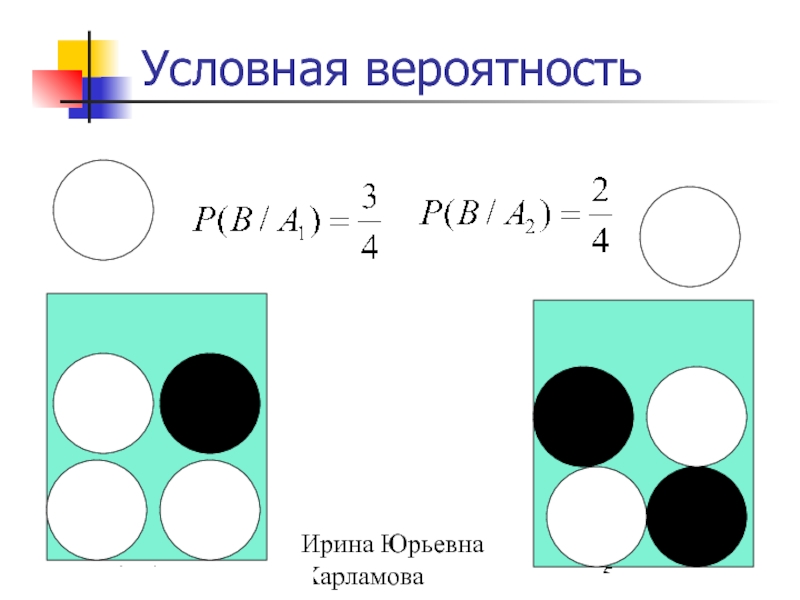
В – событие "вынутый шар - белый",
А1 -событие
"шар вынимается из 1-ой урны",
А2 -событие "шар вынимается из 2-ой урны"
А2 -событие "шар вынимается из 2-ой урны"
1
2
Слайд 6События А и В называются независимыми
если осуществление одного не влияет
на вероятность осуществления другого, т.е.
или
или
Слайд 8ТЕОРЕМА 1
Вероятность совместного появления двух событий равна произведению вероятности одного из
них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
Слайд 10ТЕОРЕМА 2
Вероятность совместного появления двух независимых событий равна произведению их вероятностей,
т.е.
Слайд 1109/03/2019
Ирина Юрьевна Харламова
ТЕОРЕМА 2
Усложненное строение буквы «а» за чет повторения движения
в овале Р(А)=0,06
Буква «д» с надстрочечным элементом Р(В)=0,29
Слайд 13ТЕОРЕМА 4
Вероятность совместного наступления конечного числа событий равна произведению вероятности одного
из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже наступили, т.е.
Слайд 1409/03/2019
Ирина Юрьевна Харламова
Ю
Р
И
С
Т
А1 – первая буква «ю»,
А2 – вторая буква «р»,
А3 – третья буква «и»,
А4 – третья
буква «с»,
А5 – пятая буква «т».
В ‑ появится слово «юрист».
А5 – пятая буква «т».
В ‑ появится слово «юрист».
Слайд 16ТЕОРЕМА 5
Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению
вероятностей этих событий, т.е.
Слайд 19ТЕОРЕМА 6
Вероятность появления одного из двух несовместных событий, равна сумме вероятностей
этих событий, т.е.
Слайд 2009/03/2019
Ирина Юрьевна Харламова
25 ЧЕЛОВЕК ИМЕЮТ СЛЕДУЮЩИЕ ОЦЕНКИ
ОТЛИЧНО -
ХОРОШО -
УДОВЛЕТВОРИТЕЛЬНО -
5
10
10
Слайд 2109/03/2019
Ирина Юрьевна Харламова
Какова вероятность того, что наугад вызванный курсант отличник или
хорошист?
Слайд 2209/03/2019
Ирина Юрьевна Харламова
А – наугад вызванный курсант –
отличник,
В – наугад вызванный
курсант – хорошист.
Слайд 23ТЕОРЕМА 7
Вероятность появления одного из нескольких попарно несовместных событий равна сумме
вероятностей этих событий
Слайд 24СЛЕДСТВИЕ
Сумма вероятностей попарно несовместных событий, образующих полную группу, равна 1:
Слайд 2509/03/2019
Ирина Юрьевна Харламова
Два стрелка стреляют по одной и той же цели.
Вероятности поражения ими цели соответственно равны 0,8 и 0,7.
Какова вероятность поражения цели?
Какова вероятность поражения цели?
Слайд 2609/03/2019
Ирина Юрьевна Харламова
А1 – поражение цели первым стрелком,
А2 – поражение цели вторым стрелком,
В –
поражение цели вообще
Слайд 27ТЕОРЕМА 8
Вероятность появления хотя бы одного из двух совместных событий равна
сумме вероятностей этих событий без вероятности их совместного наступления:
Слайд 30ТЕОРЕМА 9
Вероятность появления хотя бы одного из событий, независимых в совокупности,
равна разности между единицей и произведением вероятностей противоположных событий:
Слайд 33ТЕОРЕМА 10
Вероятность события А, которое может наступить только при условии появления
одного из событий В1, В2,...,Вn, образующих полную группу попарно несовместных событий, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А, т.е.
Слайд 3409/03/2019
Ирина Юрьевна Харламова
Вероятность того, что во время работы ПК произошел сбой:
в арифметическом устройстве 0,3,
в оперативной памяти – 0,2,
в остальных устройствах – 0,5.
Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8, 0,9, 0,9.
Найти вероятность того, что возникший в ПК сбой будет обнаружен.
в оперативной памяти – 0,2,
в остальных устройствах – 0,5.
Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8, 0,9, 0,9.
Найти вероятность того, что возникший в ПК сбой будет обнаружен.
Слайд 3509/03/2019
Ирина Юрьевна Харламова
Обозначим через А событие – сбой будет обнаружен. Возможны
следующие предположения (гипотезы):
В1 – сбой произошел в арифметическом устройстве,
В2 – сбой произошел в оперативной памяти,
В3 – сбой произошел в остальных устройствах.
Воспользуемся формулой полной вероятности:
В1 – сбой произошел в арифметическом устройстве,
В2 – сбой произошел в оперативной памяти,
В3 – сбой произошел в остальных устройствах.
Воспользуемся формулой полной вероятности:
Слайд 36Алгоритм применения ф.Байеса
1. Выдвигают предположения – гипотезы В1, В2,...,Вn. Данные гипотезы составляют
полную группу несовместных событий.
Слайд 37Алгоритм применения ф.Байеса
2. Устанавливают доопытные (априорные) вероятности данных гипотез: из интуитивных или
каких-либо других соображений.
Слайд 38Алгоритм применения ф.Байеса
3. Проводят эксперимент, в результате которого происходит событие А.
Таким
образом получают новую информацию, на основании которой выполняют переоценку доопытных вероятностей гипотез по формуле Байеса:
Слайд 39Алгоритм применения ф.Байеса
где Р(А) определяется по формуле полной вероятности.
Т.о. заменяют доопытные
(априорные) вероятности гипотез послеопытными (апостериорными).
Слайд 4009/03/2019
Ирина Юрьевна Харламова
Вероятность обнаружить признак А в рукописи, выполненной женщиной равна
0,1, а в рукописи, выполненной мужчиной – 0,3.
На исследование поступила рукопись, в которой обнаружен данный признак. Какова вероятность, что данная рукопись выполнена женщиной? Какова вероятность, что данная рукопись выполнена мужчиной?
На исследование поступила рукопись, в которой обнаружен данный признак. Какова вероятность, что данная рукопись выполнена женщиной? Какова вероятность, что данная рукопись выполнена мужчиной?
Слайд 4109/03/2019
Ирина Юрьевна Харламова
А – в рукописи обнаружен признак А;
М – рукопись
выполнена мужчиной;
Ж – рукопись выполнена женщиной.
Ж – рукопись выполнена женщиной.
Слайд 4209/03/2019
Ирина Юрьевна Харламова
А – в рукописи обнаружен признак А;
М – рукопись
выполнена мужчиной;
Ж – рукопись выполнена женщиной.
Ж – рукопись выполнена женщиной.
