- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхні другого порядку презентация
Содержание
- 1. Поверхні другого порядку
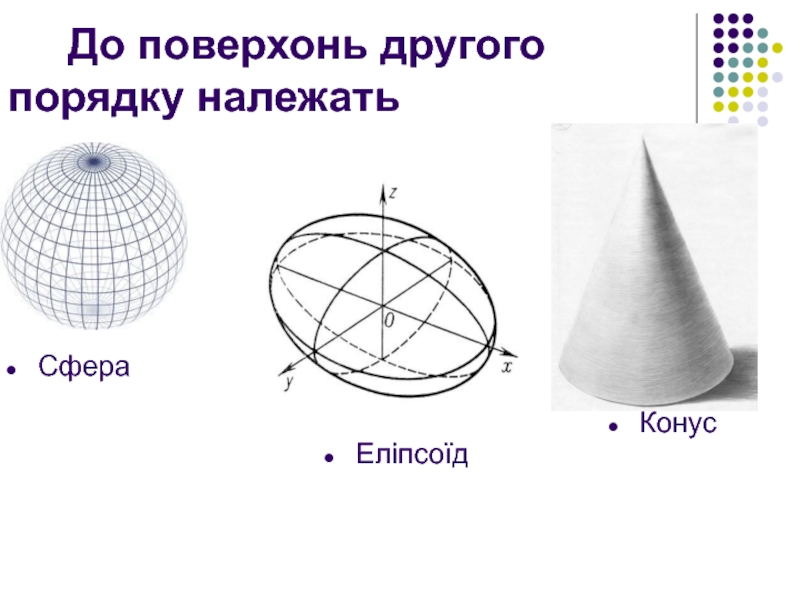
- 3. До поверхонь другого порядку належать Сфера Еліпсоїд Конус
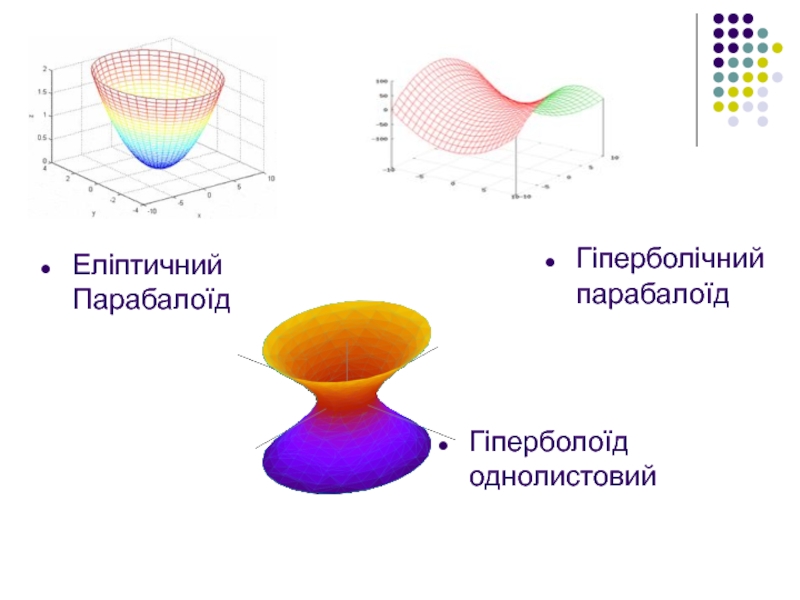
- 4. Еліптичний Парабалоїд Гіперболічний парабалоїд Гіперболоїд однолистовий
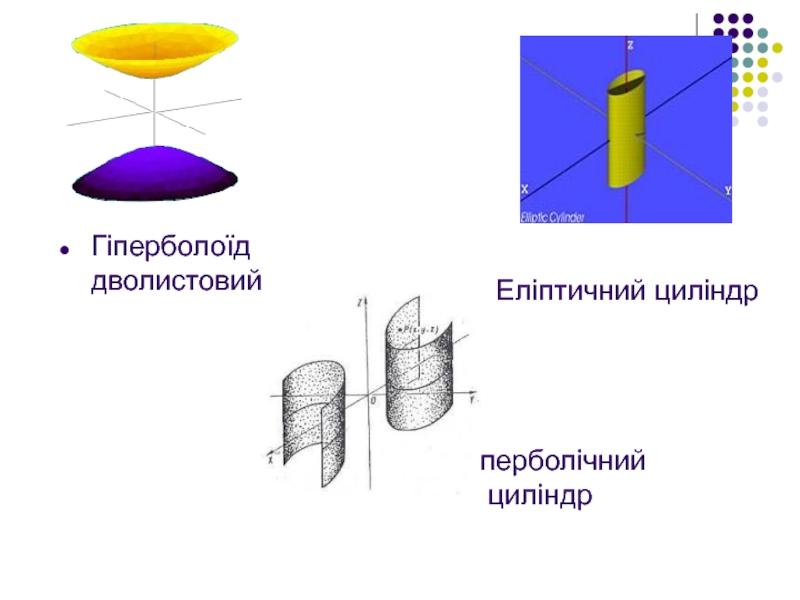
- 5. Гіперболічний циліндр Гіперболоїд дволистовий Еліптичний циліндр
- 6. Параболічний циліндр
- 9. Основні формули конуса Об'єм конуса R-радіус
- 11. Еліпсоїд — замкнута центральна поверхня другого порядку. Еліпсоїд
- 12. Основні Формули еліпсоїда Площа поверхні: Для стислого еліпсоїда Об'єм
- 13. Гіперболо́їд— вид поверхні другого порядку в тривимірному просторі, що
- 14. Якщо a = b, то така поверхня зветься — гіперболоїд обертання. Однопорожнинний
- 15. Лінійчата конструкція, що має форму однополостного гіперболоїда,
- 16. Використання форми конуса Вафельні стаканчики
- 17. М’ячик для гандболу Використання форми еліпса
- 18. Використання форми еліптичного параболоїда Середньовічний шолом Вуличний Ліхтар
- 19. Приклади з
- 20. Використання форми еліптичного циліндра Світильник Обігрівач
- 21. Використання гіперболоїда Його форму активно використовують в архітектурі.
Слайд 2 История
Першу інформацію
Вчені, які займалися вивченням властивостей поверхонь 2 порядку
Евклід
Евдокс Кнідський
Архімед
Слайд 7 Сфера
Сфера
Рівняння
де (x0 ,y0,z0)-координати центру сфери, R-її
радіус.
Основні геометричні формули
Площа сфери
r-радіус
Об'єм кулі, що обмежена сферою
r-радіус
Площа сегмента сфери
H-висота сегмента; θ - зенітний кут
(x − x0)2 + (y − y0)2 + (z − z0)2 = R2
Слайд 8
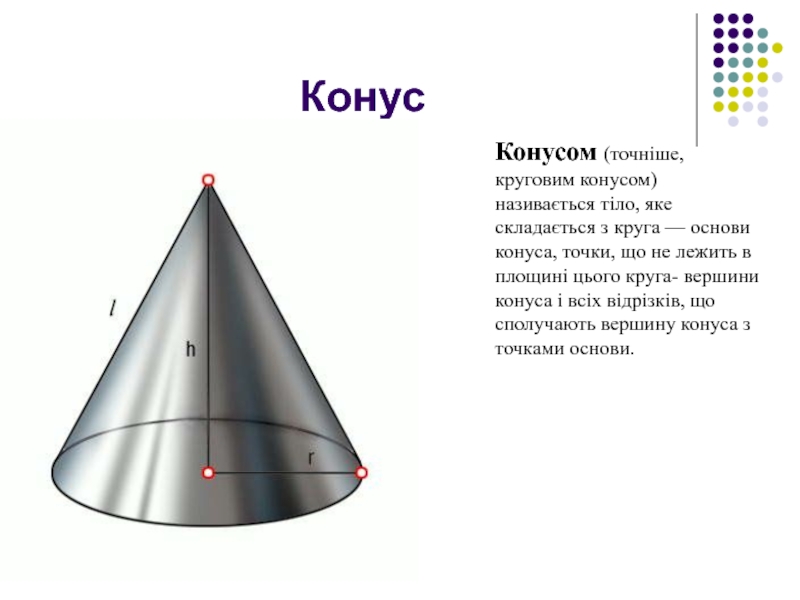
Конусом (точніше, круговим конусом) називається тіло, яке складається з круга — основи конуса, точки, що не лежить в площині цього круга- вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи.
Слайд 9Основні формули конуса
Об'єм конуса
R-радіус основи; H-висота
Площа бічної поверхні конуса
R-радіус основи; l-довжина
Кут при вершині прямого конуса
-кут між двома протилежними твірними
α
Слайд 10 Сфера
Сфера
Рівняння
де (x0 ,y0,z0)-координати центру сфери, R-її
радіус.
Основні геометричні формули
Площа сфери
r-радіус
Об'єм кулі, що обмежена сферою
r-радіус
Площа сегмента сфери
H-висота сегмента; θ - зенітний кут
(x − x0)2 + (y − y0)2 + (z − z0)2 = R2
Слайд 11Еліпсоїд — замкнута центральна поверхня другого порядку. Еліпсоїд має центр симетрії та
Точки перетину координатних осей з еліпсоїдом називаються його вершинами.
Рівняння
Кординати (a;b;c) – називаються напіосями еліпсоїда
Еліпсоїд
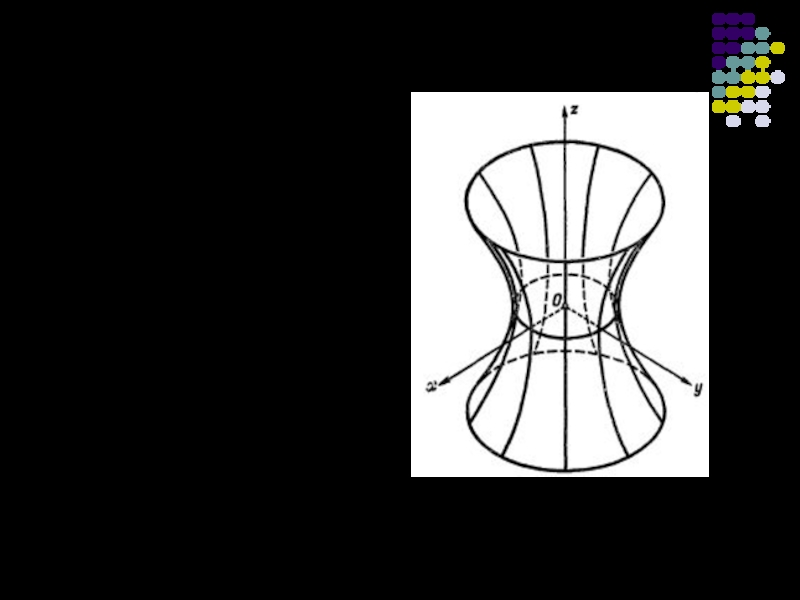
Слайд 13Гіперболо́їд— вид поверхні другого порядку в тривимірному просторі, що задається в Декартових координатах рівнянням
(Однопорожнинний гіперболоїд), формула
де a і b- дійсні півосі, а c- уявна піввісь
(двопорожнинний гіперболоїд),
де a і b — уявні півосі, а c- дійсна піввісь.
або
Слайд 14Якщо a = b, то така поверхня зветься — гіперболоїд обертання. Однопорожнинний гіперболоїд обертання можна отримати обертанням
Слайд 15Лінійчата конструкція, що має форму однополостного гіперболоїда, є жорсткої: якщо балки з'єднати
В архітектурі
Слайд 16Використання форми конуса
Вафельні стаканчики для морозива.
Дорожній конус використовується як обгороження
Слайд 19 Приклади з життя сфери
Найелементарнішим прикладом сфери
Розваги на воді. Повітряна куля.