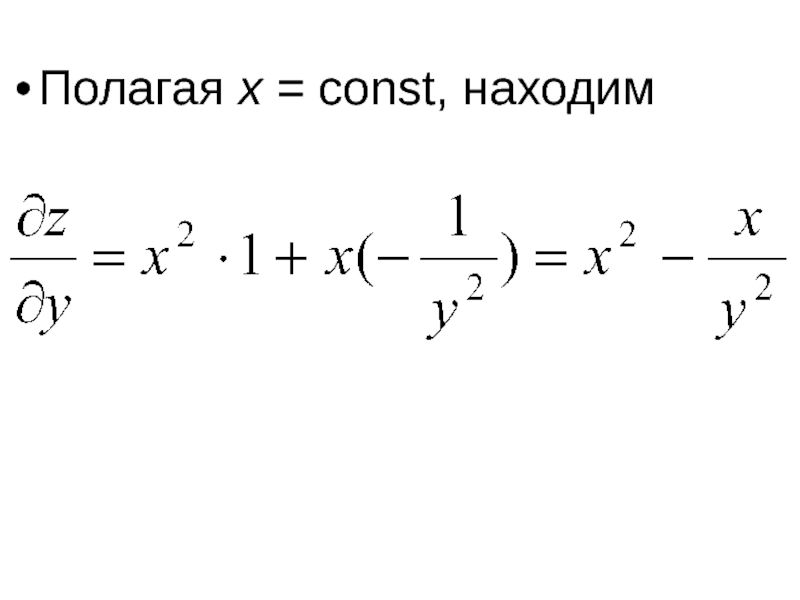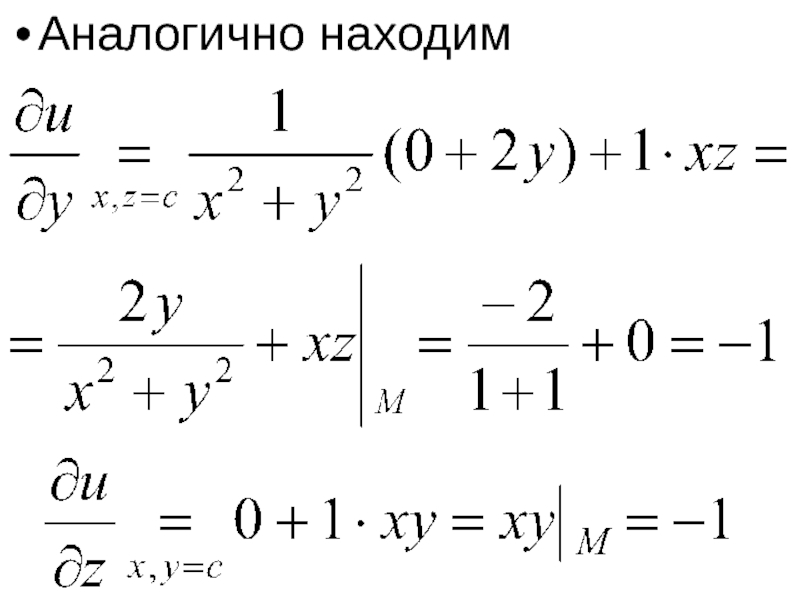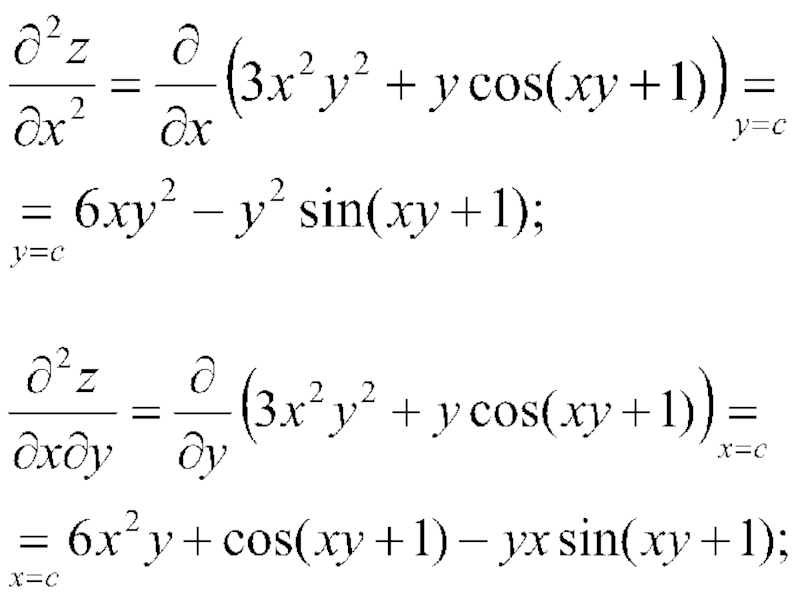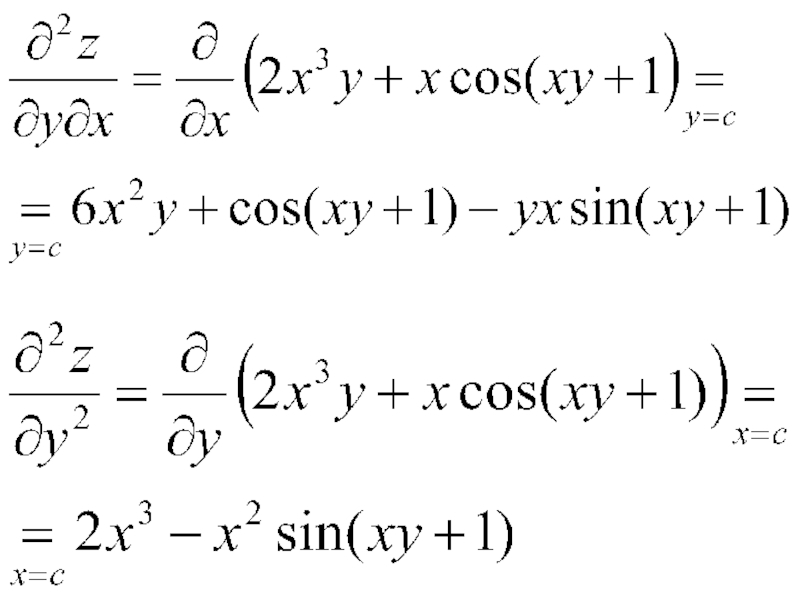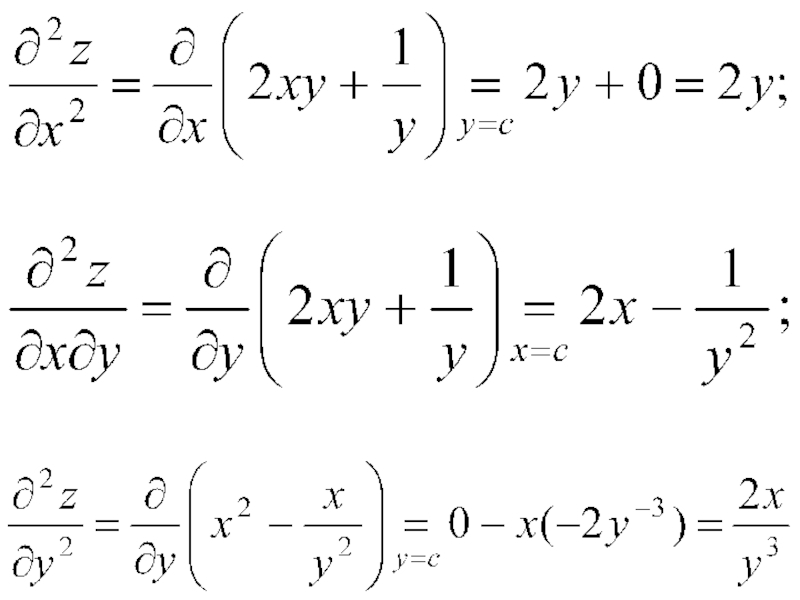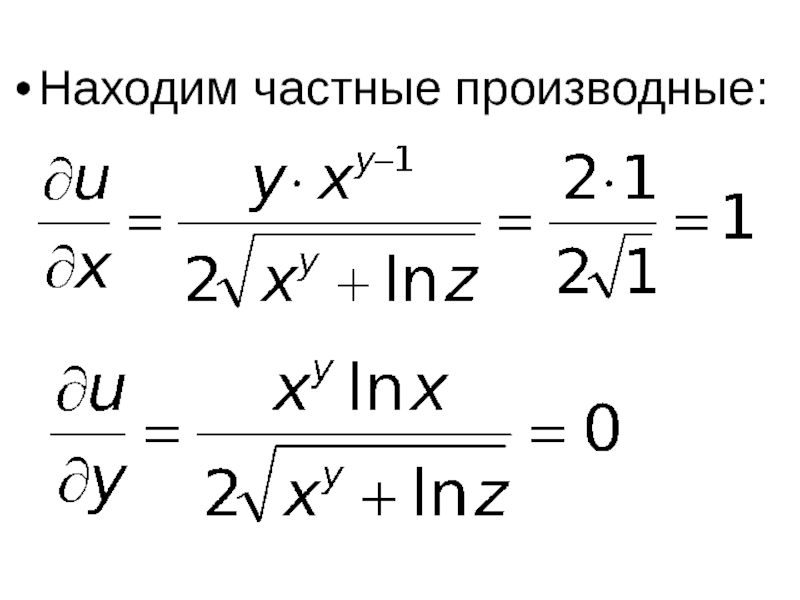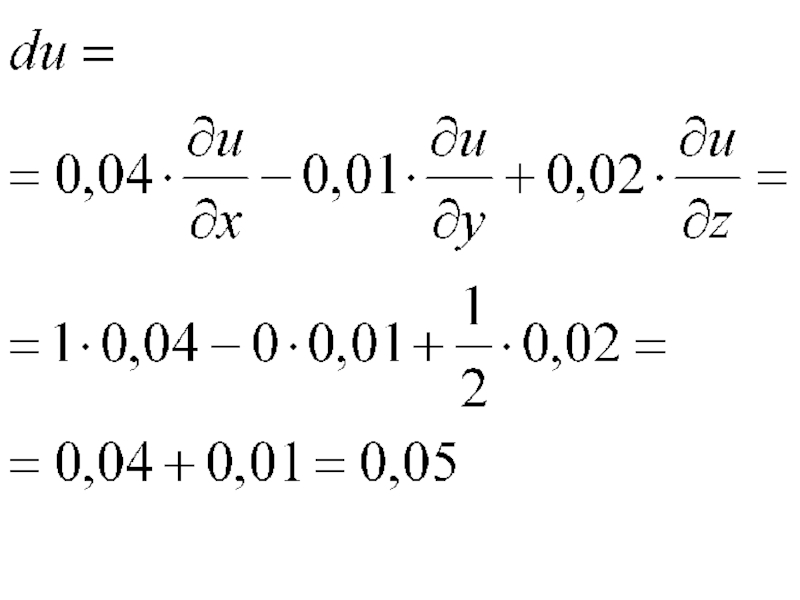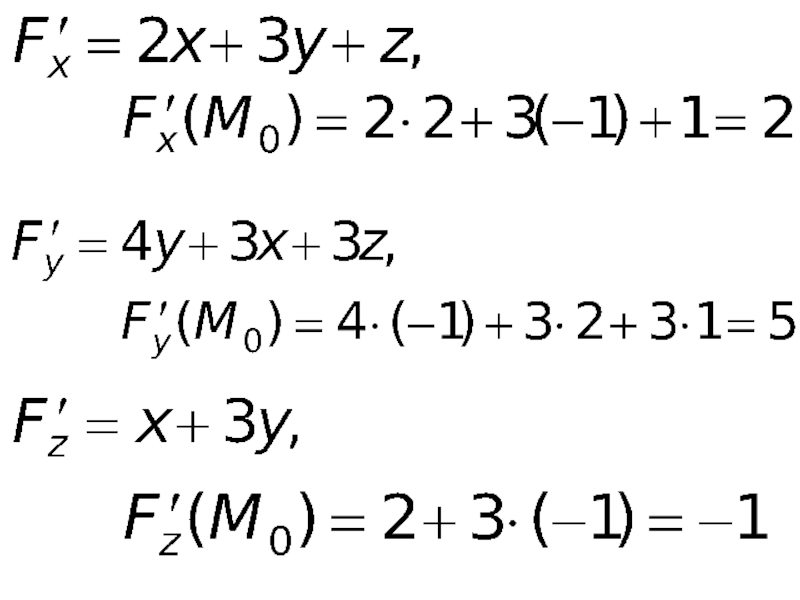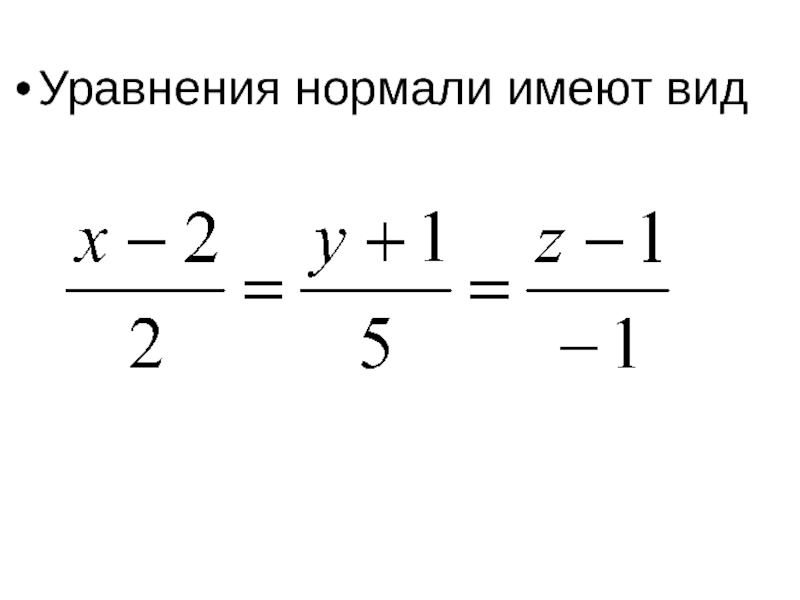- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Частные производные функции презентация
Содержание
- 1. Частные производные функции
- 2. Решение. Полагая y = const, находим
- 3. Полагая x = const, находим
- 4. Пример. Найти значения частных производных функции в точке M(1, –1, 0).
- 5. Решение. Полагая y = const, z = const, находим
- 6. Аналогично находим
- 7. Геометрическим смыслом частной производной (например,
- 8. Предположим, что функция z = f(x, y) имеет непрерывные частные производные
- 9. Эти производные в свою очередь являются функциями
- 10. Частными производными 2-го порядка называются частные производные
- 12. В общем случае смешанные частные производные могут
- 13. Частными производными n–го порядка называются частные производные
- 14. Частные производные любого порядка, взятые по различным переменным, называются смешанными.
- 15. Пример. Найти частные производные 2-го порядка функции
- 16. Решение. Последовательно находим
- 19. § 5. Дифференциал функции нескольких переменных
- 20. Рассмотрим функцию z = f(x, y). Дадим аргументу x приращение
- 21. Предположим, что f(x, y) в точке M(x, y) имеет непрерывные частные производные.
- 22. Определение. Дифференциалом 1-го порядка функции z = f(x, y) называется
- 23. Так как дифференциалы независимых переменных совпадают с
- 24. Геометрическим смыслом полного дифференциала функции двух переменных
- 25. Геометрический смысл полного дифференциала функции двух переменных
- 26. Дифференциалом 2-го порядка функции z = f(x, y) называется дифференциал
- 27. Если все частные производные 2-го порядка функции z = f(x, y) непрерывны, то имеет место формула:
- 28. Аналогично определяется дифференциал n–го порядка:
- 29. Пример. Найти дифференциалы 1-го и 2-го порядков функции
- 30. Решение. Найдем частные производные 1-го и 2-го порядков:
- 32. Следовательно, дифференциалы 1-го и 2-го порядков запишутся в виде:
- 33. Приближенные вычисления с помощью полного дифференциала
- 34. Пусть функция f(x, y) дифференцируема в точке
- 35. Если подставить в эту формулу выражение то получим приближенную формулу:
- 36. Пример. Вычислить приближенно значение
- 37. Решение. Из заданного выражения определим
- 38. Находим частные производные:
- 39. Полный дифференциал функции u равен:
- 41. Точное значение этого выражения: 1,049275225687319176.
- 42. § 6. Касательная плоскость и нормаль к поверхности
- 43. Касательной плоскостью к поверхности в ее точке
- 44. Нормалью к поверхности в точке M0 называется
- 46. Если поверхность задана уравнением F(x, y, z) = 0 то уравнение касательной плоскости в точке M0(x0, y0, z0) имеет вид:
- 47. Уравнения нормали, проведенной к поверхности в точке M0(x0, y0, z0), запишутся следующим образом:
- 48. Если поверхность задана уравнением z = f(x, y), то уравнение касательной плоскости в точке M0(x0, y0, z0) имеет вид:
- 49. а уравнения нормали запишутся так:
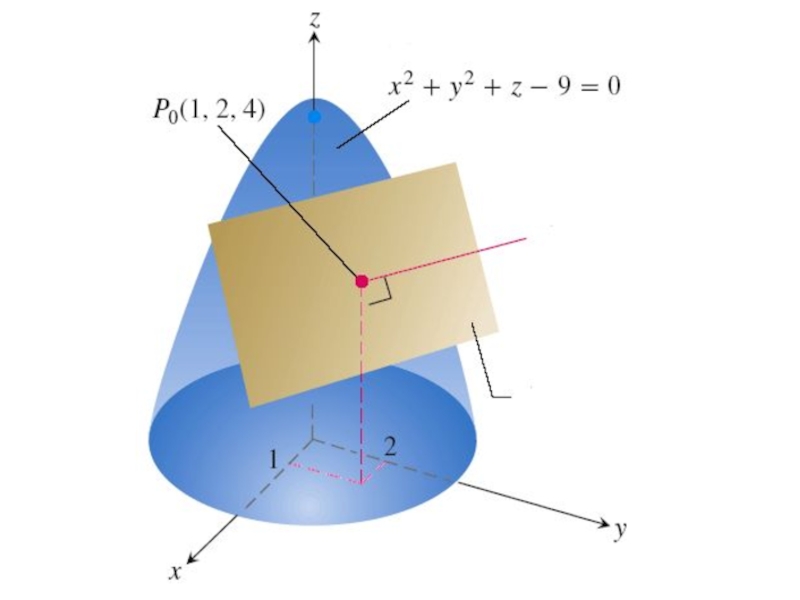
- 50. Пример. Составить уравнения касательной плоскости и нормали
- 51. Решение. Подставляя x0 и y0 в уравнение
- 52. По условию задачи поверхность задана неявно. Обозначим
- 54. Подставляем найденные значения частных производных в уравнение касательной плоскости
- 55. и получаем искомое уравнение касательной плоскости:
- 56. Уравнения нормали имеют вид
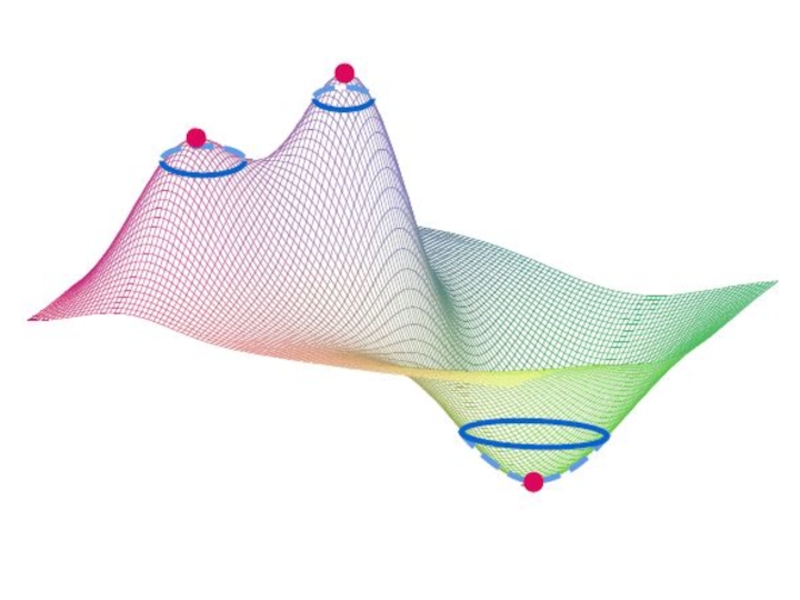
- 57. § 7. Экстремум функции двух переменных
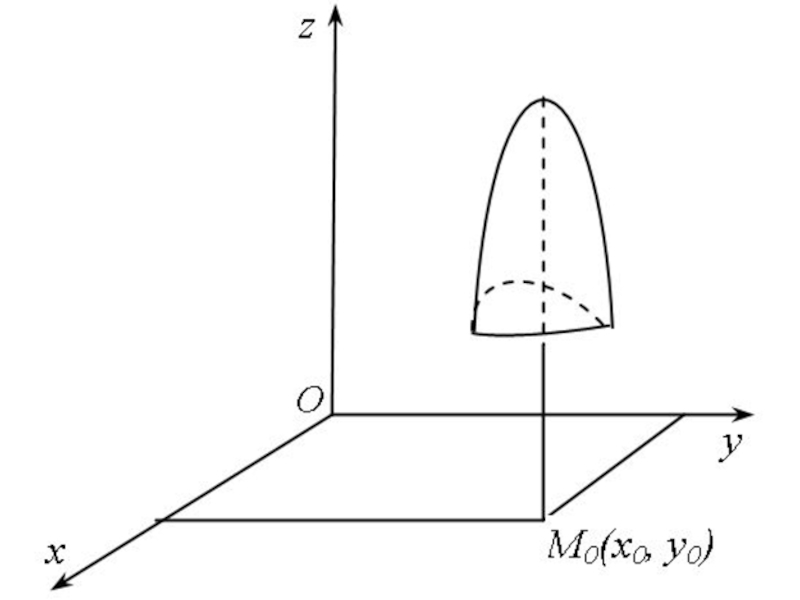
- 58. Определение. Функция z = f(x, y) имеет максимум в точке
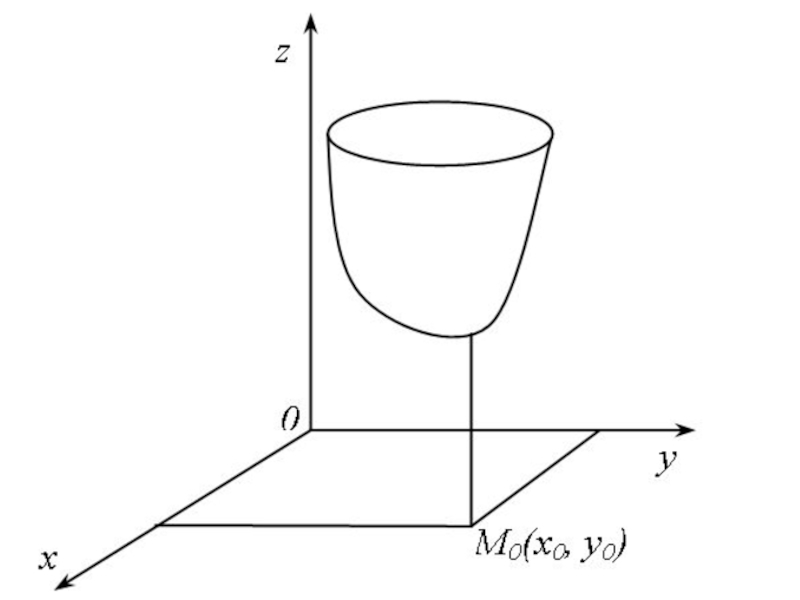
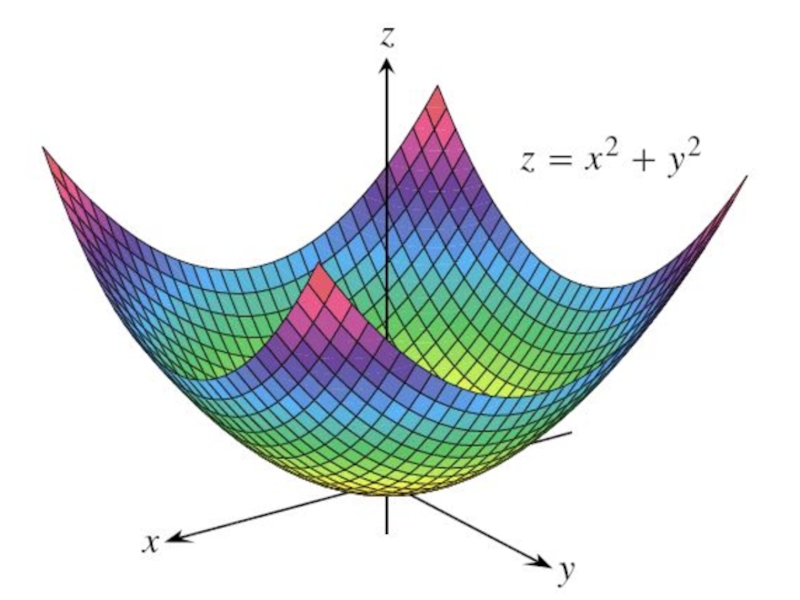
- 60. Определение. Функция z = f(x, y) имеет минимум в точке
- 62. Точки максимума и минимума называют точками экстремума, а значения функции в этих точках называются экстремальными.
- 64. Теорема 1 (необходимые условия экстремума). Если дифференцируемая
- 65. Функция z = f(x, y) может иметь экстремум и в
- 66. Теорема 2 (достаточные условия экстремума). Пусть M0(x0, y0)
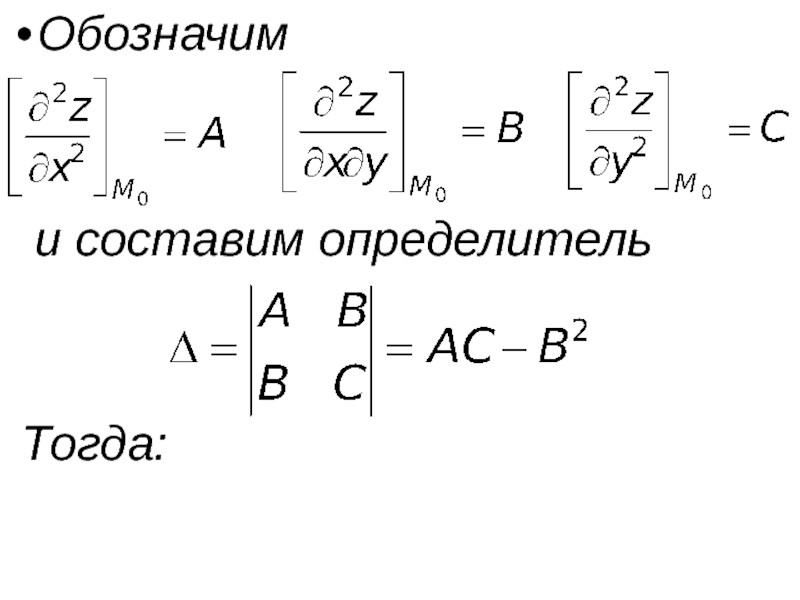
- 67. Обозначим и составим
- 68. 1) если Δ 0, то в точке M0
- 72. Пример. Исследовать на экстремум функцию
- 73. Решение. Находим частные производные 1-го порядка
- 74. Стационарные точки найдем из системы уравнений
- 75. Получили две стационарные точки: M1(0, 0), и M2(1, 1).
- 76. Находим частные производные 2-го порядка: Исследуем каждую стационарную точку.
- 77. В точке M1(0, 0) имеем:
- 78. В точке M2(1, 1) имеем:
Слайд 7Геометрическим смыслом частной производной (например, ) является
тангенс угла наклона касательной, проведенной в точке M0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
Слайд 9Эти производные в свою очередь являются функциями независимых переменных x и
y. Будем называть
и частными производными 1-го порядка.
и частными производными 1-го порядка.
Слайд 10Частными производными 2-го порядка называются частные производные от частных производных 1-го
порядка.
Для функции z = f(x, y) двух переменных можно найти четыре частные производные 2-го порядка, которые обозна-чаются следующим обр-м:
Для функции z = f(x, y) двух переменных можно найти четыре частные производные 2-го порядка, которые обозна-чаются следующим обр-м:
Слайд 12В общем случае смешанные частные производные могут не совпадать, однако для
них справедлива теорема:
Теорема. Если смешанные частные производные и непрерывны в некоторой точке M(x, y), то они равны, т. е.
Теорема. Если смешанные частные производные и непрерывны в некоторой точке M(x, y), то они равны, т. е.
Слайд 13Частными производными n–го порядка называются частные производные от частных производных (n – 1)–го
порядка.
Их обозначают
и т. д.
Их обозначают
и т. д.
Слайд 20Рассмотрим функцию z = f(x, y). Дадим аргументу x приращение Δx, а аргументу y
приращение Δy. Тогда z получит приращение
которое называется полным приращением функции z.
которое называется полным приращением функции z.
Слайд 22Определение. Дифференциалом 1-го порядка функции z = f(x, y) называется главная часть полного приращения
Δz этой функции, линейная относительно Δx и Δy, обозначается символом dz или df и вычисляется по формуле
Слайд 23Так как дифференциалы независимых переменных совпадают с их приращениями, т.е. dx = Δx,
dy = Δy, то эту формулу можно записать в виде:
Слайд 24Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке
(х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Δх, у0+Δу).
Слайд 25Геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического
смысла дифференциала функции одной переменной.
Слайд 26Дифференциалом 2-го порядка функции z = f(x, y) называется дифференциал от ее дифференциала 1-го
порядка и обозначается
Слайд 27Если все частные производные 2-го порядка функции z = f(x, y) непрерывны, то имеет
место формула:
Слайд 34Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное
приращение этой функции:
Слайд 37Решение. Из заданного выражения определим
Δx = 1,04 – 1
= 0,04,
Δy = 1,99 – 2 = -0,01,
Δz = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) =
Δy = 1,99 – 2 = -0,01,
Δz = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) =
Слайд 43Касательной плоскостью к поверхности в ее точке M0 называется плоскость, которая
содержит все касательные к кривым, проведенным на поверхности через эту точку.
Слайд 44Нормалью к поверхности в точке M0 называется прямая, проходящая через эту
точку и перпендикулярная касательной плоскости, проведенной в данной точке.
Слайд 46Если поверхность задана уравнением F(x, y, z) = 0 то уравнение касательной плоскости в точке
M0(x0, y0, z0) имеет вид:
Слайд 47Уравнения нормали, проведенной к поверхности в точке M0(x0, y0, z0), запишутся следующим образом:
Слайд 48Если поверхность задана уравнением z = f(x, y), то уравнение касательной плоскости в точке
M0(x0, y0, z0) имеет вид:
Слайд 50Пример. Составить уравнения касательной плоскости и нормали к поверхности
в
точке M0(x0, y0, z0), если
Слайд 51Решение. Подставляя x0 и y0 в уравнение поверхности, находим значение z0:
откуда находим z0 = 1. Следовательно, M0(2, –1, 1) – точка касания.
Слайд 52По условию задачи поверхность задана неявно. Обозначим
и найдем частные
производные в точке M0(2, –1, 1):
Слайд 58Определение. Функция z = f(x, y) имеет максимум в точке M0(x0, y0), если существует такая
окрестность этой точки, что для любых точек M(x, y) из этой окрестности выполняется неравенство
Слайд 60Определение. Функция z = f(x, y) имеет минимум в точке M0(x0, y0), если существует такая
окрестность этой точки, что для любых точек M(x, y) из этой окрестности выполняется неравенство
Слайд 62Точки максимума и минимума называют точками экстремума, а значения функции в
этих точках называются экстремальными.
Слайд 64Теорема 1 (необходимые условия экстремума). Если дифференцируемая функция z = f(x, y) имеет экстремум
в точке M0(x0, y0), то ее частные производные в этой точке равны нулю, т. е.
Слайд 65Функция z = f(x, y) может иметь экстремум и в точках, где функция непрерывна,
но частные производные не существуют.
Точки, в которых и ,
называются стационарными точками функции z = f(x, y).
Точки, в которых и ,
называются стационарными точками функции z = f(x, y).
Слайд 66Теорема 2 (достаточные условия экстремума). Пусть M0(x0, y0) является стационарной точкой функции
z = f(x, y) и в ее окрестности существуют непрерывные частные производные 2-го порядка.
Слайд 681) если Δ 0,
то в точке M0 есть экстремум, причем максимум при A < 0
и минимум при A > 0;
3) если Δ = 0, то требуется дополнительное исследование.
и минимум при A > 0;
3) если Δ = 0, то требуется дополнительное исследование.
Слайд 77В точке M1(0, 0) имеем:
A = 0, B = –3, C = 0.
Тогда
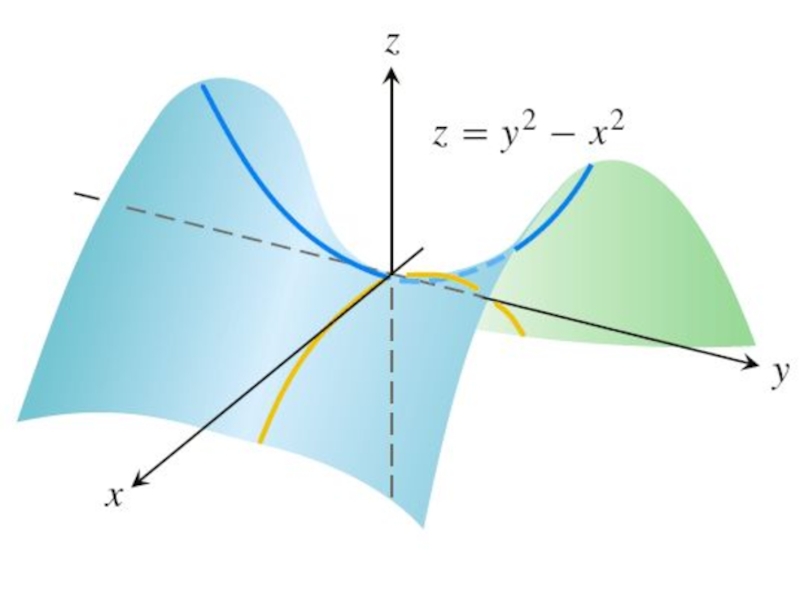
Так как Δ < 0, то в этой точке нет экстремума.
Слайд 78В точке M2(1, 1) имеем:
A = 6, B = –3, C = 6.
В
этом случае
Так как Δ > 0 и A > 0, то в этой точке функция имеет минимум
Так как Δ > 0 и A > 0, то в этой точке функция имеет минимум
