- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
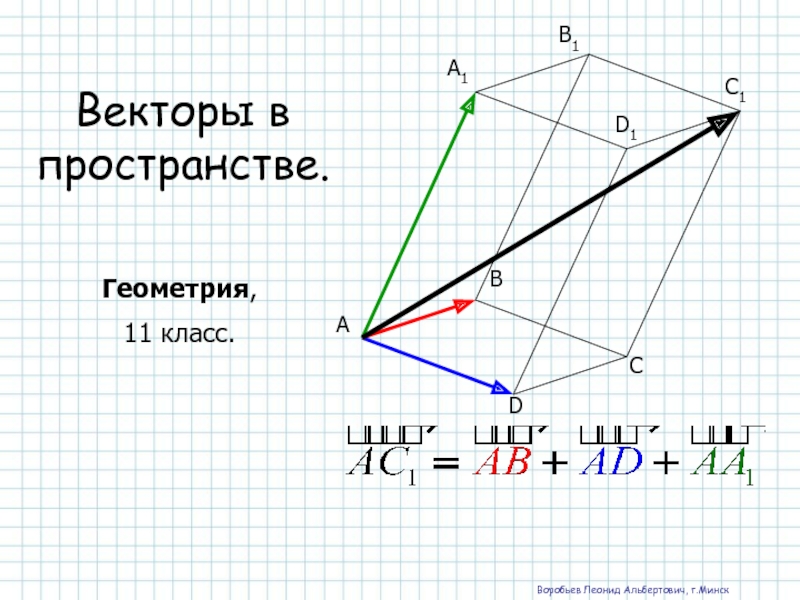
Векторы в пространстве. (11 класс) презентация
Содержание
- 1. Векторы в пространстве. (11 класс)
- 2. Как и в плоскости, в пространстве вектор
- 3. Два вектора называются коллинеарными, если они лежат
- 4. От произвольной точки пространства можно отложить единственный
- 5. II. Действия с векторами. Векторы можно складывать
- 6. При сложении трех и более векторов применяют
- 7. Также можно найти разность двух векторов –
- 8. Сложение векторов, как и сложение чисел подчиняется
- 9. И еще одно действие с
- 10. Теперь рассмотрим все эти понятия и действия
- 11. Для сложения двух векторов, заданных координатами, нужно
- 12. Для выяснения компланарности трех векторов необходимо, чтобы
- 13. Аналитически выяснить компланарность трех векторов, заданных координатами,
- 14. A B C D A1 B1 C1 D1
- 15. В прямоугольной системе координат в пространстве векторы
- 16. Умение выполнять действия с векторами и понимание
Слайд 2Как и в плоскости, в пространстве вектор определяется как направленный отрезок:
A
B
Точка
a
Обычную точку в пространстве мы также можем считать вектором, у которого начало совпадает с конечной точкой. Такой вектор называется нулевым и обозначается: или .
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной величиной) вектора, т.е.
Естественно, что
I. Определение вектора. Основные понятия, связанные с векторами.
A
B
Векторы и являются противоположными. Очевидно, что:
Слайд 3Два вектора называются коллинеарными, если они лежат на одной прямой или
a
b
c
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или соноправленными) и противоположно направленными. В нашем случае:
Обозначение коллинеарных векторов:
– соноправленные векторы, , – противоположно направленные векторы.
m
n
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули равны, т.е.
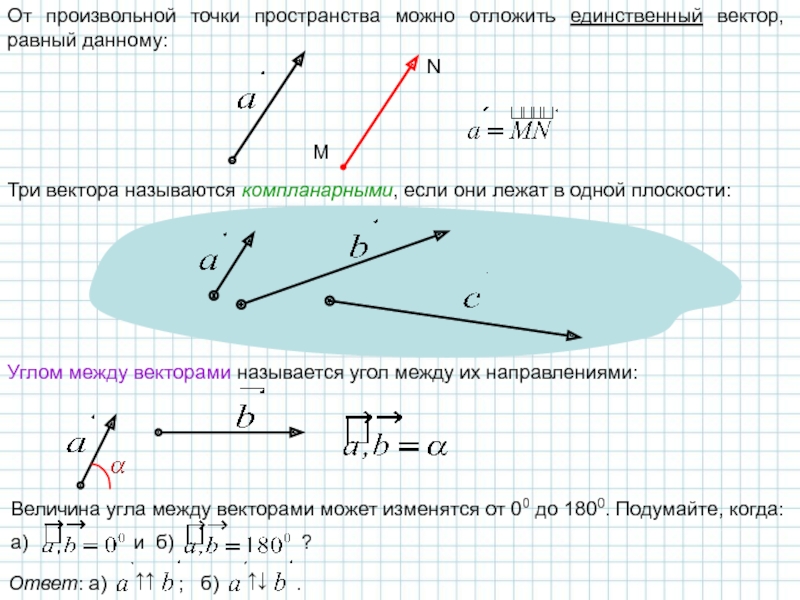
Слайд 4От произвольной точки пространства можно отложить единственный вектор, равный данному:
M
N
Три вектора
Углом между векторами называется угол между их направлениями:
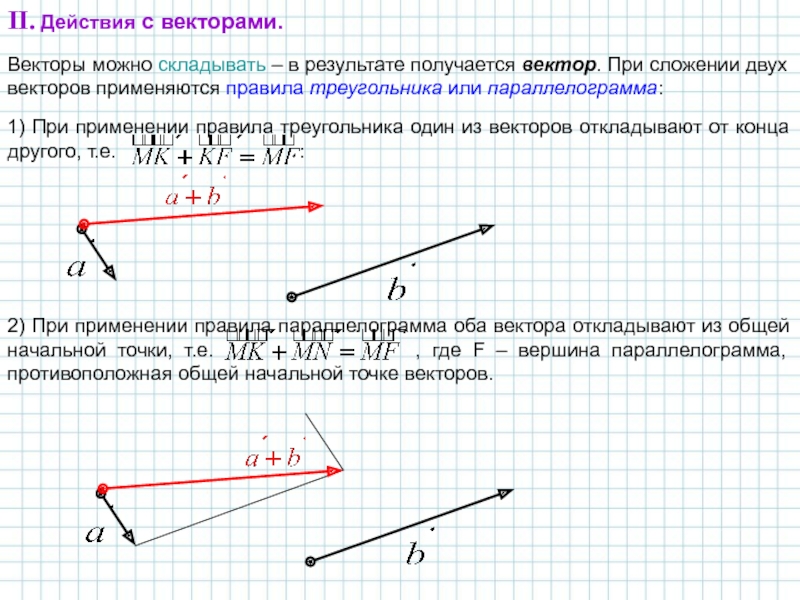
Слайд 5II. Действия с векторами.
Векторы можно складывать – в результате получается вектор.
1) При применении правила треугольника один из векторов откладывают от конца другого, т.е. :
2) При применении правила параллелограмма оба вектора откладывают из общей начальной точки, т.е. , где F – вершина параллелограмма, противоположная общей начальной точке векторов.
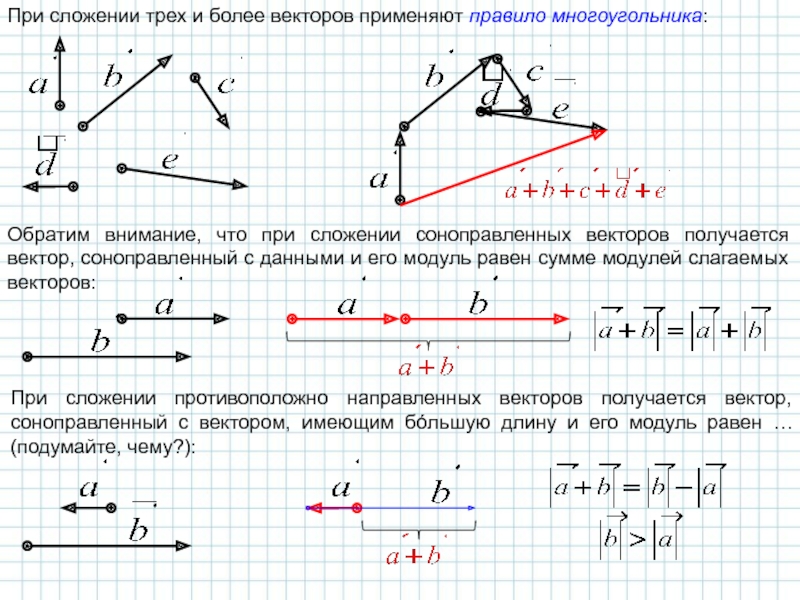
Слайд 6При сложении трех и более векторов применяют правило многоугольника:
Обратим внимание, что
При сложении противоположно направленных векторов получается вектор, соноправленный с вектором, имеющим бóльшую длину и его модуль равен … (подумайте, чему?):
Слайд 7Также можно найти разность двух векторов – в результате получается вектор.
–
Слайд 8Сложение векторов, как и сложение чисел подчиняется законам:
Следующее действие с векторами
если k>0, то и ;
если k<0, то и ;
если k=0, то .
Слайд 9
И еще одно действие с векторами – умножение двух векторов. В
Геометрически скалярное произведение векторов можно понимать как площадь параллелограмма (или противоположная ей величина), стороны которого образуются одним из данных векторов и вектором, перпендикулярным второму с таким же модулем:
α – острый угол
α – тупой угол
Слайд 10Теперь рассмотрим все эти понятия и действия с точки зрения координатного
A(x1;y1;z1)
B(x2;y2;z2)
Если принять вектор за параллельный перенос начальной точки A(x1;y1;z1) в конечную точку B(x2;y2;z2), то координаты вектора показывают: на сколько изменяются соответствующие координаты начальной точки при параллельном переносе в конечную, т.е.
Т.к. модуль вектора равен длине изображающего его отрезка, то:
III. Координаты вектора. Действия в координатах.
Слайд 11Для сложения двух векторов, заданных координатами, нужно просто сложить их соответствующие
При вычитании векторов, заданных координатами, нужно найти разности их соответствующих координат, т.е.
Умножение вектора, заданного координатами, на число выполняется так:
Скалярное произведение двух векторов, заданных координатами, равно сумме произведений соответствующих координат, т.е.
Условием коллинеарности двух векторов, заданных координатами, будет пропорциональность их соответствующих координат:
Самостоятельно разберитесь, когда и .
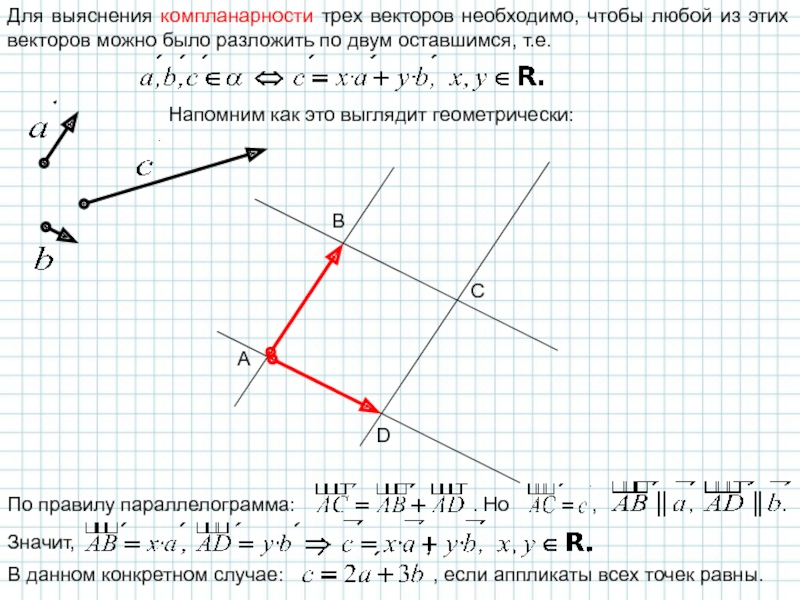
Слайд 12Для выяснения компланарности трех векторов необходимо, чтобы любой из этих векторов
A
B
C
D
Напомним как это выглядит геометрически:
Слайд 13Аналитически выяснить компланарность трех векторов, заданных координатами, можно решая систему:
Если система
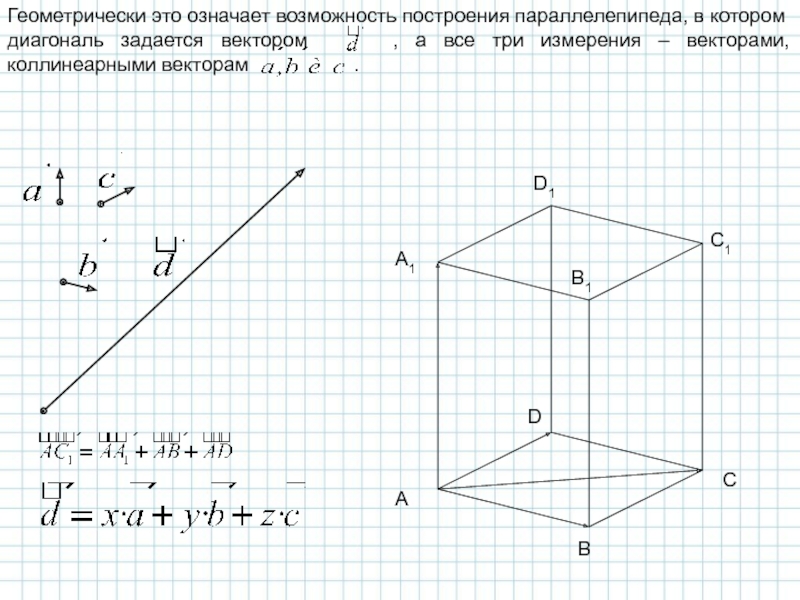
Любой вектор пространства можно разложить по трем некомпланарным векторам, т.е.
Аналитически разложение любого вектора по трем некомпланарным векторам сводится к решению системы:
А решение этой системы – числа x, y и z являются коэффициентами разложения вектора по трем векторам
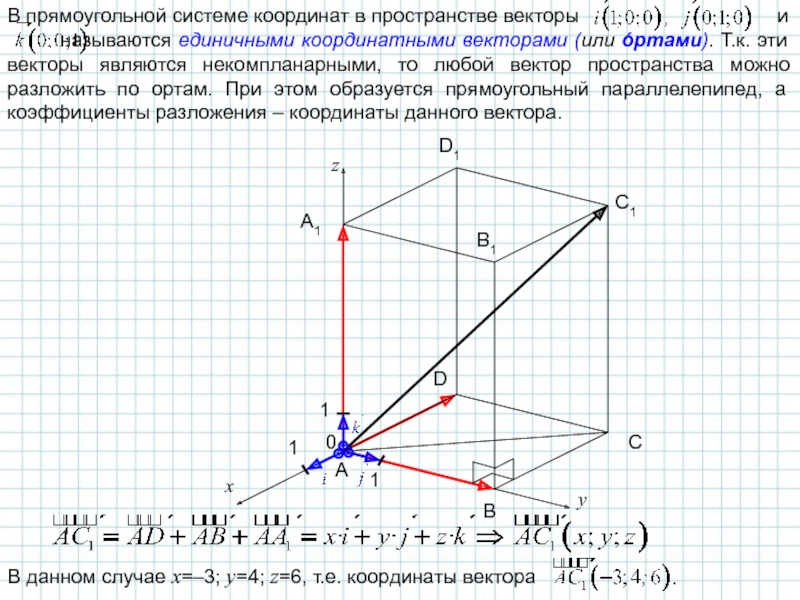
Слайд 15В прямоугольной системе координат в пространстве векторы
x
y
z
A
B
C
D
A1
B1
C1
D1
0
1
1
1
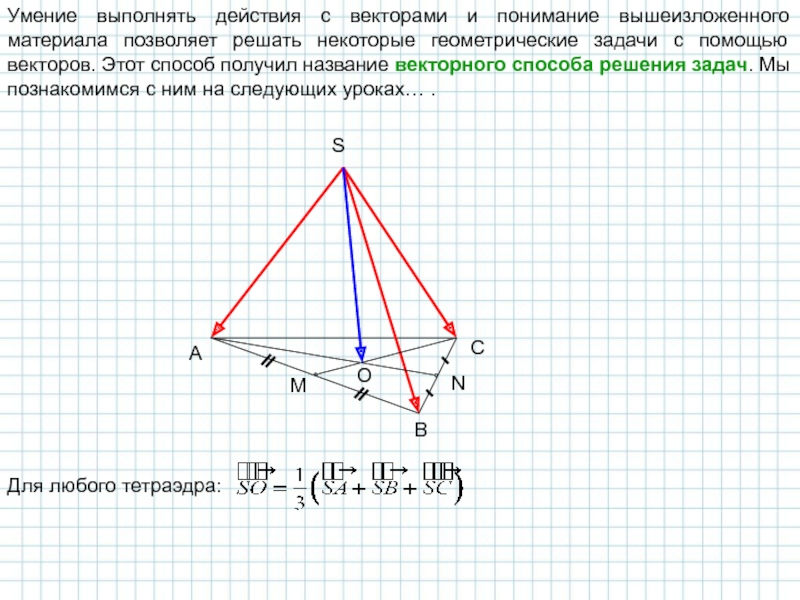
Слайд 16Умение выполнять действия с векторами и понимание вышеизложенного материала позволяет решать
A
B
C
M
N
S
O