- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Части графа. Операции над частями графа презентация
Содержание
- 1. Части графа. Операции над частями графа
- 2. Часть графа Пусть
- 3. Суграф Подграф Н
- 4. Подграф, порожденным множеством
- 5. Звездный граф Подграф
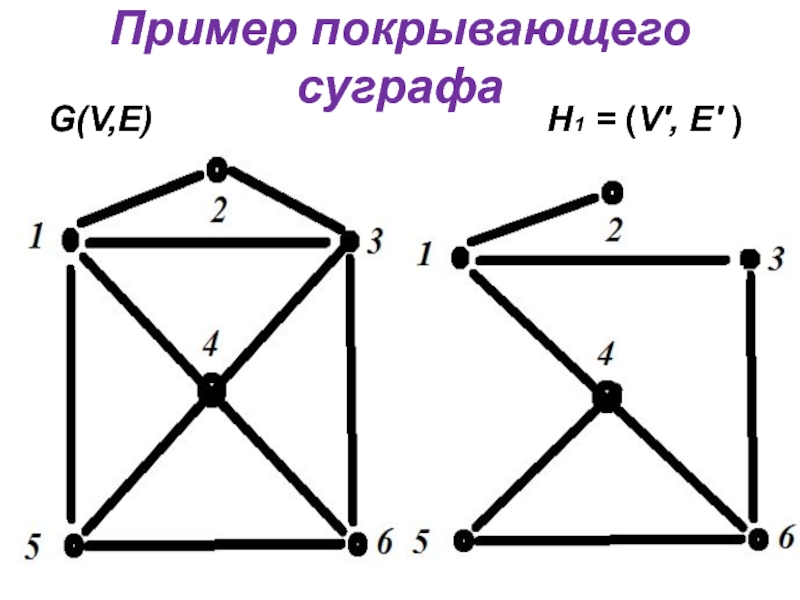
- 6. Пример покрывающего суграфа G(V,E)
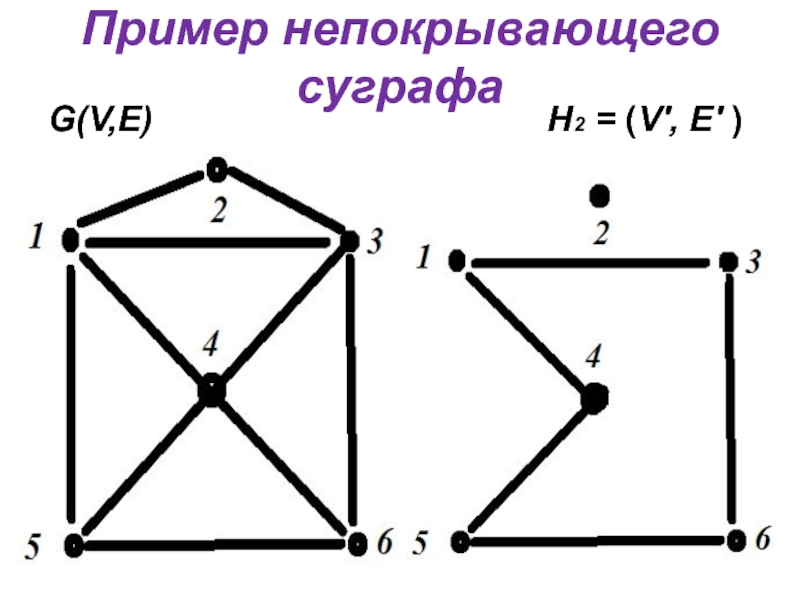
- 7. Пример непокрывающего суграфа G(V,E)
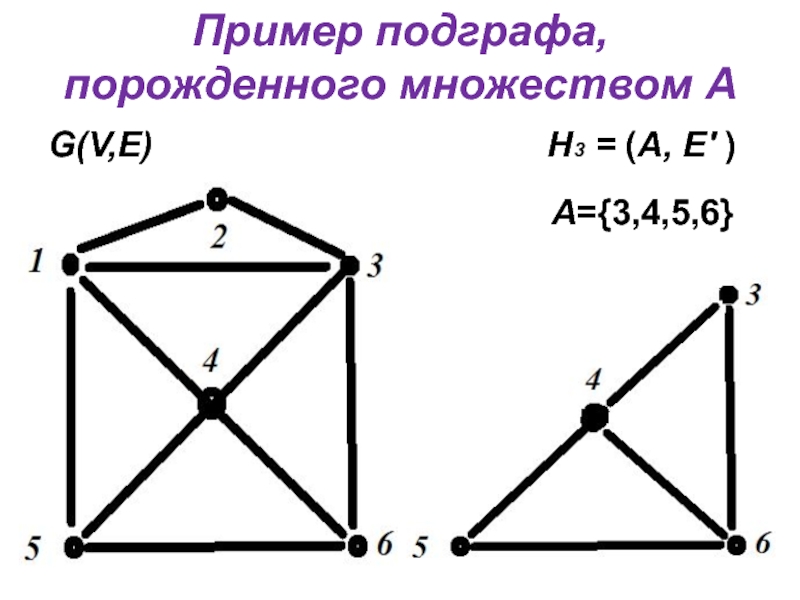
- 8. Пример подграфа, порожденного множеством А G(V,E)
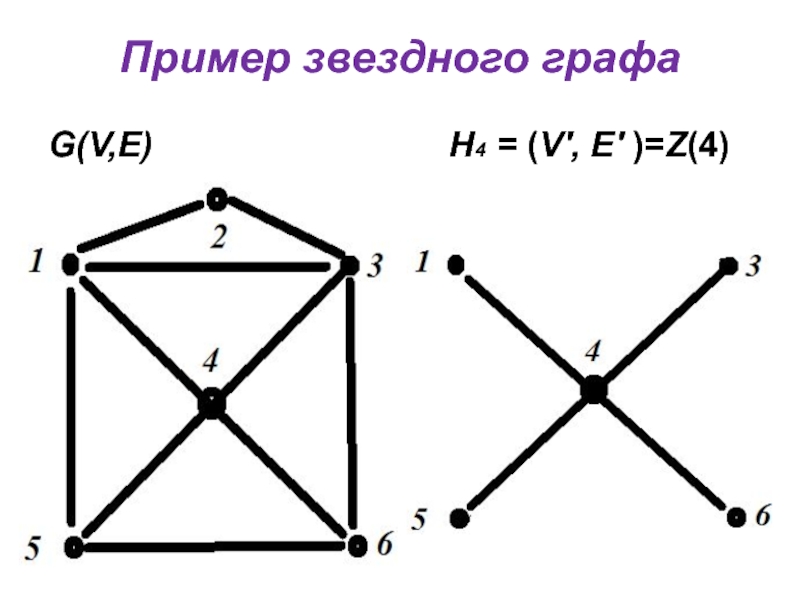
- 9. Пример звездного графа G(V,E)
- 10. Операции над частями
- 11. Операции над частями
- 12. Операции над частями
- 13. Операции над частями
- 14. Операции над частями
- 15. Операции над частями
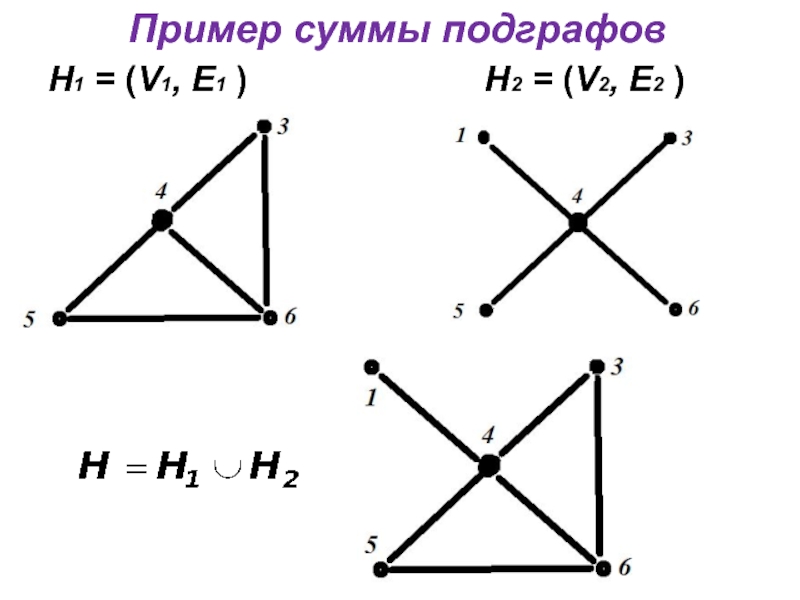
- 16. Пример суммы подграфов Н1 = (V1, E1
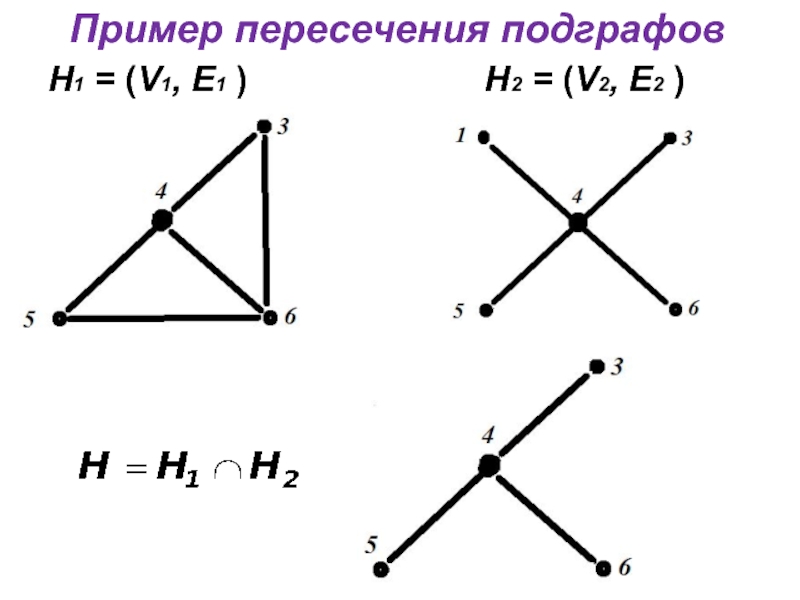
- 17. Пример пересечения подграфов Н1 = (V1, E1
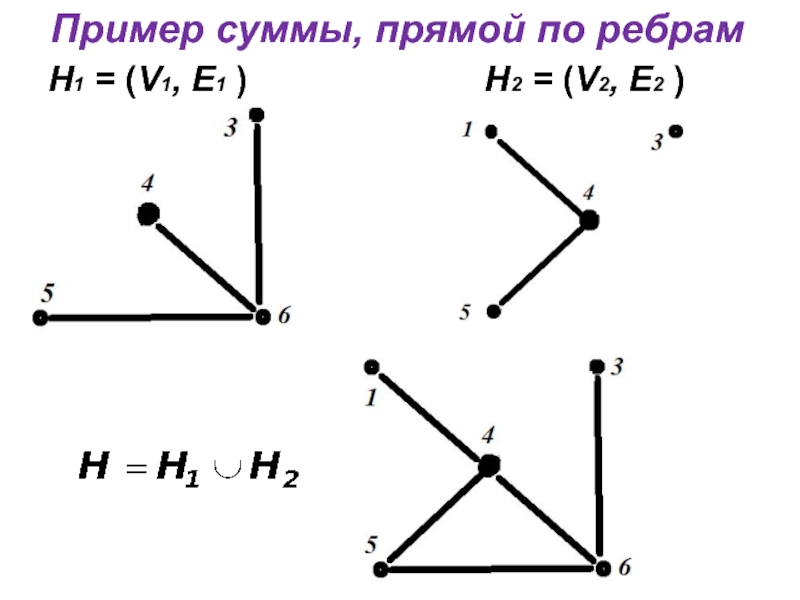
- 18. Пример суммы, прямой по ребрам Н1 =
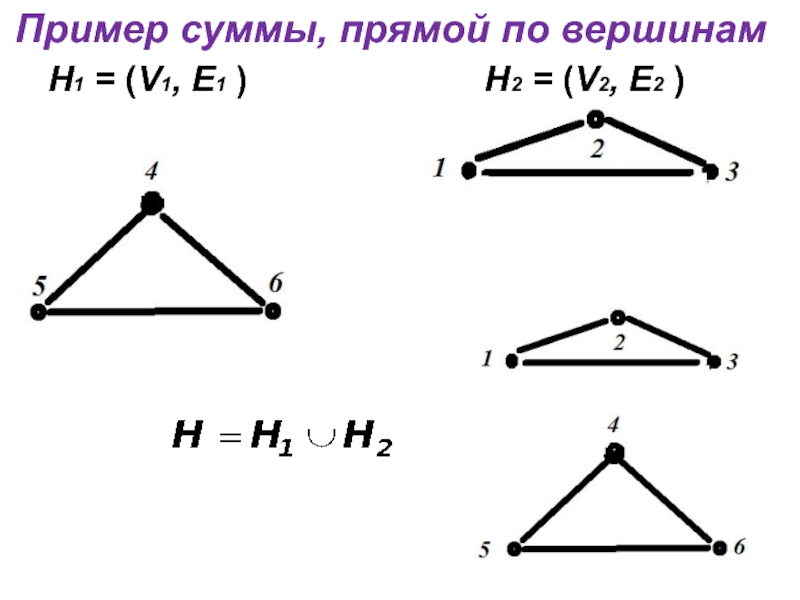
- 19. Пример суммы, прямой по вершинам Н1 =
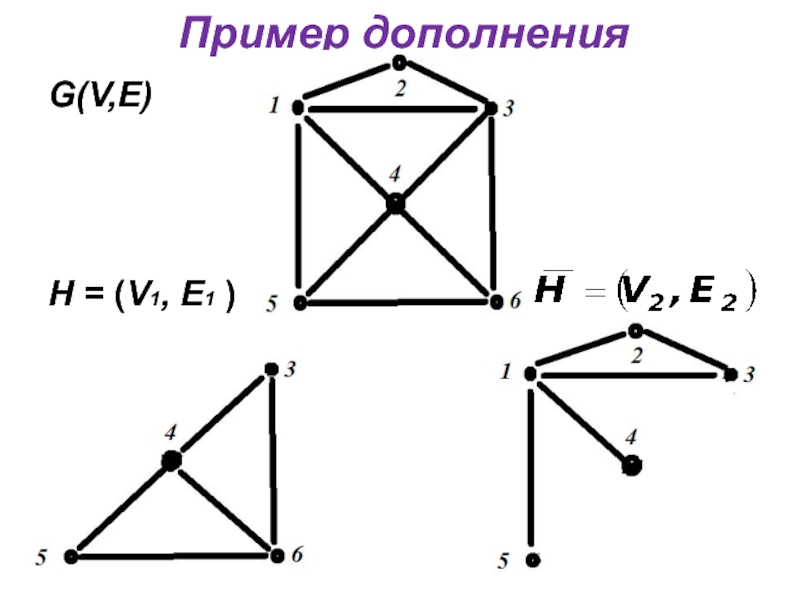
- 20. Пример дополнения G(V,E)
- 21. Замечание Подграф и его дополнение являются прямой суммой по ребрам:
Слайд 2
Часть графа
Пусть G =(V, E) – н-граф.
Частью (подграфом) графа G
называется
граф Н =(V', E' ),
где V' V, E' E ,
причем все ребра множества E' входят в граф Н вместе со своими концами.
где V' V, E' E ,
причем все ребра множества E' входят в граф Н вместе со своими концами.
Слайд 3
Суграф
Подграф Н =(V', E' ), называется суграфом, если V' = V.
Суграф
называется покрывающим, если каждая вершина инцидентна хотя бы одному ребру графа G.
Слайд 4
Подграф, порожденным множеством вершин
Подграф Н = (V', E' ), называется подграфом,
порожденным множеством вершин А V,
если V' = А, E' состоит из ребер множества Е, соединяющих вершины множества А.
если V' = А, E' состоит из ребер множества Е, соединяющих вершины множества А.
Слайд 5
Звездный граф
Подграф Н = (V', E' ), называется звездным графом вершины
если V' составляют вершина v и все смежные ей вершины,
E' состоит из ребер множества Е, инцидентных вершине v.
Слайд 10
Операции над частями графа
Суммой подграфов
Н1 = (V1, E1 ) и
Н2 = (V2, E2 ) называется граф Н = (V, E ),
такой что
Обозначается:
такой что
Обозначается:
Слайд 11
Операции над частями графа
Пересечением подграфов
Н1 = (V1, E1 ) и
Н2 = (V2, E2 ) называется граф D= (V, E ),
такой что
Обозначается:
такой что
Обозначается:
Слайд 12
Операции над частями графа
Сумма подграфов
Н1 = (V1, E1 ) и
Н2 = (V2, E2 ) называется прямой по ребрам, если у них нет общих ребер:
Слайд 13
Операции над частями графа
Сумма подграфов
Н1 = (V1, E1 ) и
Н2 = (V2, E2 ) называется прямой по вершинам, если у них нет общих вершин:
Слайд 14
Операции над частями графа
Дополнением подграфа
Н = (V1, E1 ) до
графа G = (V, E ) называется подграф
где множество его ребер:
где множество его ребер:
Слайд 15
Операции над частями графа
а множество вершин V2 состоит из всех вершин
множества V, инцидентных ребрам из Е2 и всех изолированных вершин, не попавших в множество V1.