- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач С4. Планиметрия презентация
Содержание
- 1. Решение задач С4. Планиметрия
- 2. Две окружности касаются внутренним образом. Третья окружность
- 3. Решение (продолжение). б) Пусть r1 = 6, r2 = 2.
- 4. 2 На диагонали параллелограмма взяли точку, отличную
- 5. Около остроугольного треугольника ABC описана окружность с
- 6. Окружность с центром O, вписанная в треугольник
- 7. Окружность с центром O, вписанная в треугольник
- 8. Биссектриса угла ADC параллелограмма ABCD пересекает прямую
- 9. В треугольник ABC вписана окружность радиуса R,
- 10. Радиусы окружностей с центрами O1 и O2
- 11. 7 Радиусы окружностей с центрами O1 и
- 12. Угол C треугольника ABC равен 30°, D
- 13. Угол C треугольника ABC равен 30°, D
- 14. В окружности проведены хорды PQ и CD,
- 15. В окружности проведены хорды PQ и
- 16. Окружности радиусов 1 и 4 с центрами
- 17. Окружности радиусов 1 и 4 с центрами
- 18. Решение. (1 случай) Т.к. ∠АВО1 = 15°
- 19. 11 Окружности радиусов 3 и 5 с
- 20. Окружность радиуса 6 вписана в угол, равный
- 21. Окружность радиуса 6 вписана в угол, равный
- 22. Решить самостоятельно (АНАЛОГИЧНО ПРЕДЫДУЩЕЙ ЗАДАЧЕ). 13
- 23. Две стороны треугольника равны 8 и 10,
- 24. Две стороны треугольника равны 8 и 10,
- 25. Расстояния от точки M, расположенной внутри прямого
- 26. Окружность, вписанная в треугольник ABC, площадь которого
- 27. Вневписанной окружностью треугольника называется окружность, касающаяся одной
- 28. Вневписанной окружностью треугольника называется окружность, касающаяся одной
- 29. Дан прямоугольник KLMN со сторонами: KN =
- 30. Дан прямоугольник KLMN со сторонами: KN =
- 31. Боковые стороны KL и MN трапеции KLMN
- 32. Боковые стороны KL и MN трапеции KLMN
- 33. Дан равнобедренный треугольник с боковой стороной 4
- 34. Дан равнобедренный треугольник с боковой стороной 4
- 35. В треугольнике ABC известны стороны: AB =
- 36. Решение. (1 случай) ∆AOB = ∆COD =
- 37. Решение. (2 случай) ∆AOB = ∆COD =
- 38. Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает
- 39. 24
- 40. 25 Решение. а) по свойству касательных к
- 41. 25
- 42. К окружности, вписанной в квадрат ABCD,
- 43. К окружности, вписанной в квадрат ABCD, проведена
- 44. На гипотенузе KL равнобедренного прямоугольного треугольника
- 45. На гипотенузе KL равнобедренного прямоугольного треугольника KLM
- 46. 28 Ответ: 135.
- 47. Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает
- 48. 30 Точка М пересечения медиан треугольника ABC,
- 49. 30 Точка М пересечения медиан треугольника ABC,
- 50. Продолжение следует!
Слайд 1Решение задач С4
Планиметрия
Учитель математики: Семёнова Елена Юрьевна
МБОУ СОШ №5 – «Школа
Слайд 2Две окружности касаются внутренним образом. Третья окружность касается первых двух и
Решение.
a) Найдем периметр ∆О1О2О3
(т.е. диаметру большей окружности)
1
Слайд 3
Решение (продолжение).
б) Пусть r1 = 6, r2 = 2. Тогда
Две окружности касаются внутренним образом.
1
Слайд 42
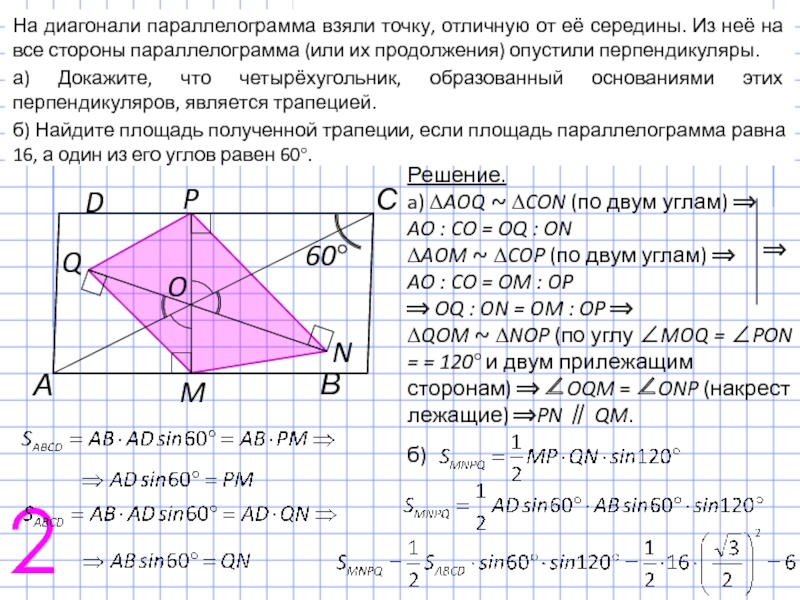
На диагонали параллелограмма взяли точку, отличную от её середины. Из неё
а) Докажите, что четырёхугольник, образованный основаниями этих перпендикуляров, является трапецией.
б) Найдите площадь полученной трапеции, если площадь параллелограмма равна 16, а один из его углов равен 60°.
Решение.
a) ∆AOQ ~ ∆CON (по двум углам) ⟹
AO : CO = OQ : ON
∆AOM ~ ∆COP (по двум углам) ⟹
AO : CO = OM : OP
⟹ OQ : ON = OM : OP ⟹
∆QOM ~ ∆NOP (по углу ∠MOQ = ∠PON = = 120° и двум прилежащим сторонам) ⟹ ∠OQM = ∠ONP (накрест лежащие) ⟹PN ∥ QM.
б)
⟹
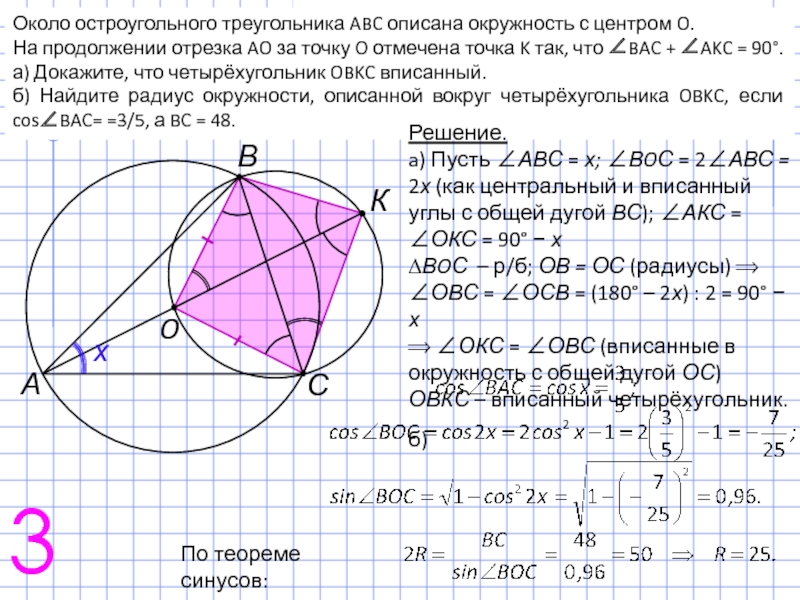
Слайд 5Около остроугольного треугольника ABC описана окружность с центром O.
На продолжении
а) Докажите, что четырёхугольник OBKC вписанный.
б) Найдите радиус окружности, описанной вокруг четырёхугольника OBKC, если cos∠BAC= =3/5, а BC = 48.
Решение.
a) Пусть ∠АВС = х; ∠ВOС = 2∠АВС = 2х (как центральный и вписанный углы с общей дугой ВС); ∠АКС = ∠ОКС = 90° − х
∆ВOС – р/б; ОВ = ОС (радиусы) ⟹
∠ОВС = ∠ОСВ = (180° – 2х) : 2 = 90° − х
⟹ ∠ОКС = ∠ОВС (вписанные в окружность с общей дугой ОС)
ОВКС – вписанный четырёхугольник.
б)
По теореме синусов:
3
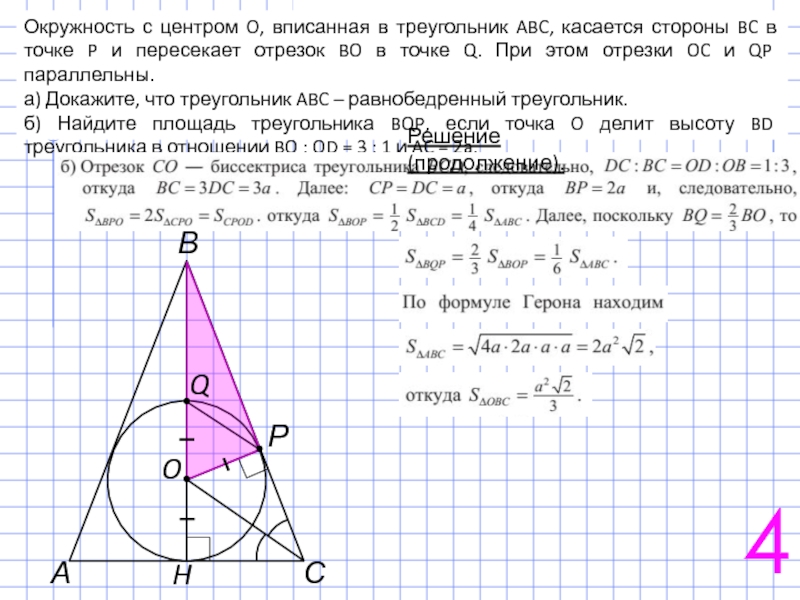
Слайд 6Окружность с центром O, вписанная в треугольник ABC, касается стороны BC
а) Докажите, что треугольник ABC – равнобедренный треугольник.
б) Найдите площадь треугольника BQP, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2a.
Решение.
4
Слайд 7Окружность с центром O, вписанная в треугольник ABC, касается стороны BC
а) Докажите, что треугольник ABC – равнобедренный треугольник.
б) Найдите площадь треугольника BQP, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2a.
Решение (продолжение).
4
Слайд 8Биссектриса угла ADC параллелограмма ABCD пересекает прямую AB в точке E.
а) Докажите, что прямые KT и DE параллельны.
б) Найдите угол BAD, если известно, что AD = 6 и KT = 3.
Решение.
a) ∠АDE = ∠СDE = ∠АED (как накрест лежащие при параллельных прямых
AB и DC и секущей DE)
∆AOT = ∆AOK (по общей гипотенузе и катетам ОТ = ОК = r) ⟹ AT = AK ⟹
∆ATK – р/б ⟹ ∠ATK = ∠AKT
∆AKT ~ ∆AED (по общему углу А и двум прилежащим сторонам) ⟹ ∠ATK =
= ∠ADE – соответственные ⟹ KT ∥ DE
б) ∆ADE – р/б; AD = AE = 6, АР – высота и медиана ⟹ DP = EP. Пусть АТ = АК = х, тогда TD = PD = 6 – x, т. к. ∆AKT ~ ∆AED ⟹ AT : AD = KT : ED, x : 6 = 3 : 2(6 – x) ⟹ x = 3.
Значит, ∆AKT и ∆AED – равносторонние, ∠BAD = 60°.
Ответ: 60.
5
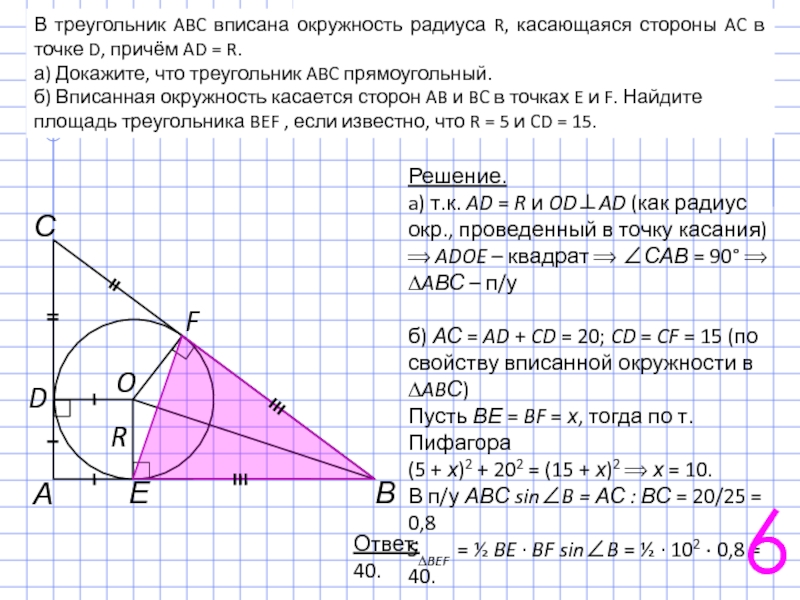
Слайд 9В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в
а) Докажите, что треугольник ABC прямоугольный.
б) Вписанная окружность касается сторон AB и BC в точках E и F. Найдите площадь треугольника BEF , если известно, что R = 5 и CD = 15.
Решение.
a) т.к. AD = R и OD⊥AD (как радиус окр., проведенный в точку касания) ⟹ ADOE – квадрат ⟹ ∠САВ = 90° ⟹ ∆AВС – п/у
б) АС = AD + CD = 20; CD = CF = 15 (по свойству вписанной окружности в ∆ABС)
Пусть ВЕ = BF = х, тогда по т. Пифагора
(5 + х)2 + 202 = (15 + х)2 ⟹ х = 10.
В п/у АВС sin∠B = АС : ВС = 20/25 = 0,8
S∆BEF = ½ BE ∙ BF sin∠B = ½ ∙ 102 ∙ 0,8 = 40.
Ответ: 40.
6
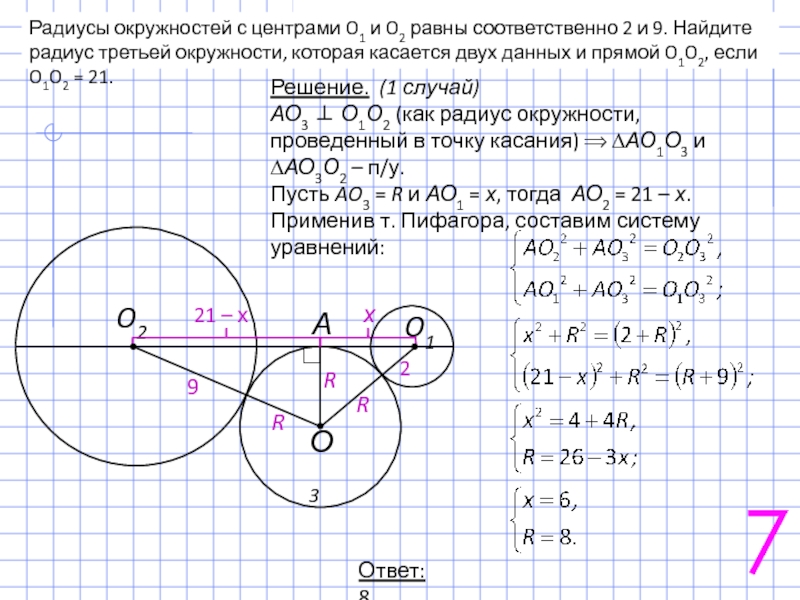
Слайд 10Радиусы окружностей с центрами O1 и O2 равны соответственно 2 и
Решение. (1 случай)
АО3 ⊥ О1О2 (как радиус окружности, проведенный в точку касания) ⟹ ∆АО1О3 и ∆АО3О2 – п/у.
Пусть AO3 = R и АО1 = х, тогда АО2 = 21 – х. Применив т. Пифагора, составим систему уравнений:
Ответ: 8.
7
Слайд 117
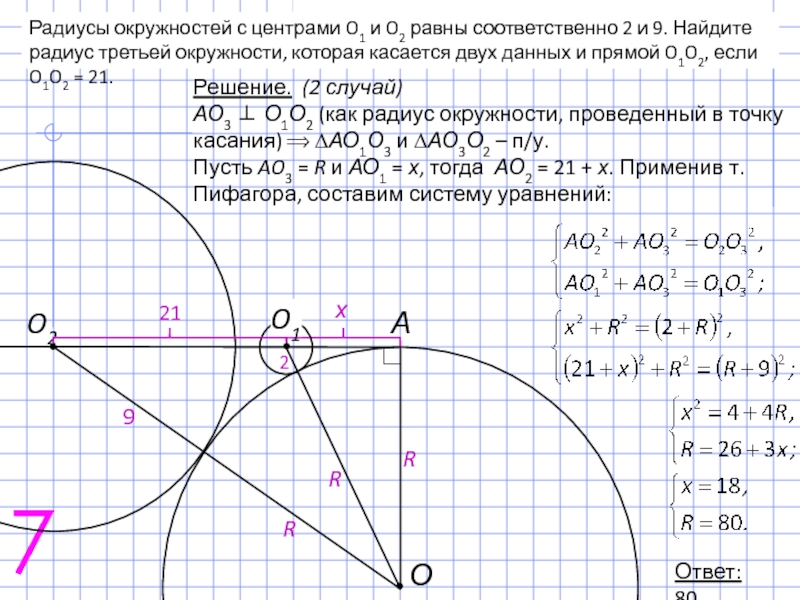
Радиусы окружностей с центрами O1 и O2 равны соответственно 2 и
Решение. (2 случай)
АО3 ⊥ О1О2 (как радиус окружности, проведенный в точку касания) ⟹ ∆АО1О3 и ∆АО3О2 – п/у.
Пусть AO3 = R и АО1 = х, тогда АО2 = 21 + х. Применив т. Пифагора, составим систему уравнений:
Ответ: 80.
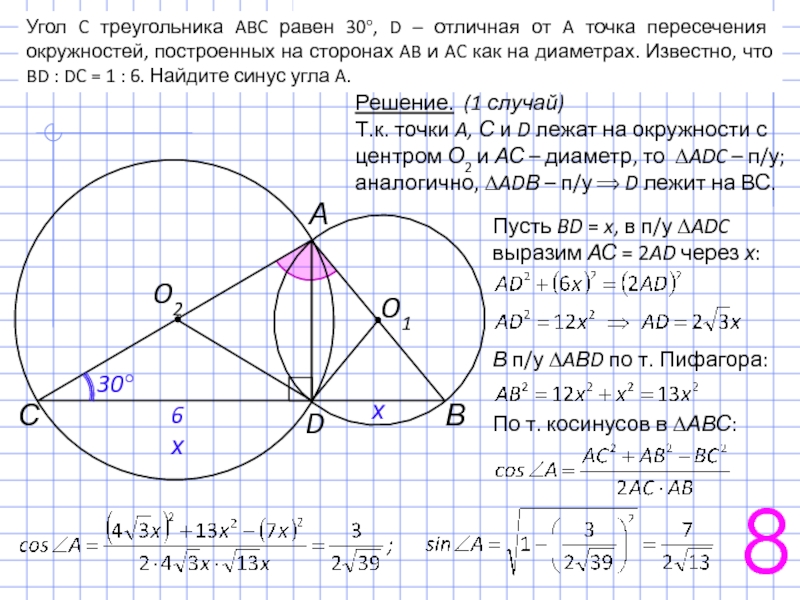
Слайд 12Угол C треугольника ABC равен 30°, D – отличная от A
Решение. (1 случай)
Т.к. точки A, С и D лежат на окружности с центром О2 и АС – диаметр, то ∆ADC – п/у; аналогично, ∆ADВ – п/у ⟹ D лежит на ВС.
Пусть BD = x, в п/у ∆ADC выразим АС = 2AD через х:
В п/у ∆AВD по т. Пифагора:
По т. косинусов в ∆АВС:
8
Слайд 13Угол C треугольника ABC равен 30°, D – отличная от A
Решение. (2 случай)
Т.к. точки A, С и D лежат на окружности с центром О2 и АС – диаметр, то ∆ADC – п/у; аналогично, ∆ADВ – п/у ⟹ D лежит на ВС.
В п/у ∆ADC выразим АС = 2AD через х:
В п/у ∆AВD по т. Пифагора:
По т. косинусов в ∆АВС:
8
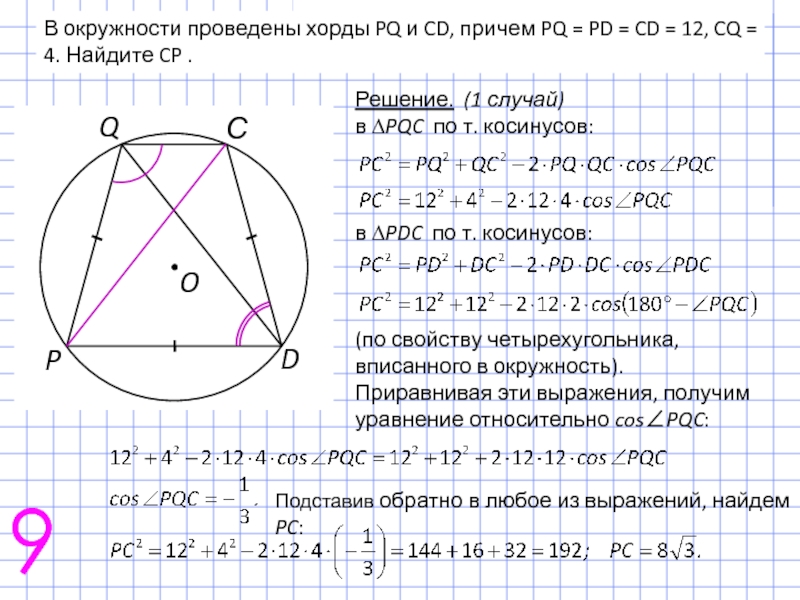
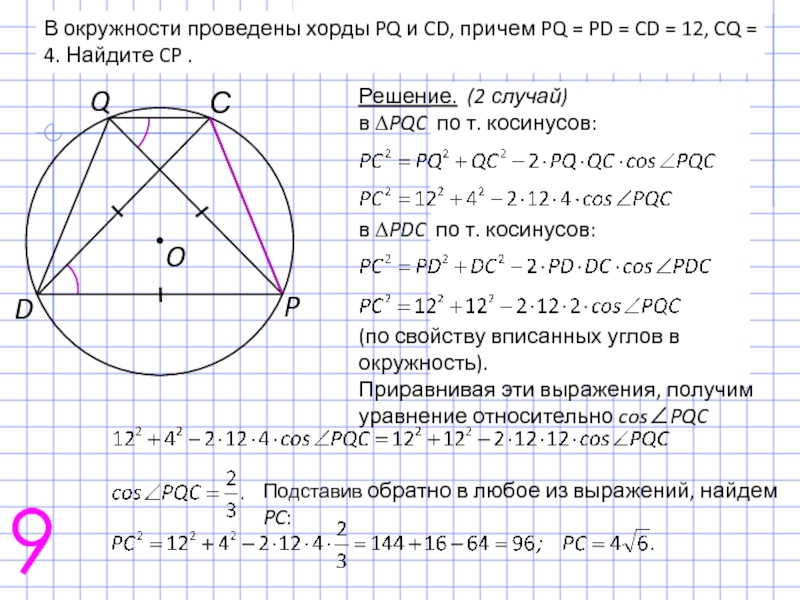
Слайд 14В окружности проведены хорды PQ и CD, причем PQ = PD
Решение. (1 случай)
в ∆PQC по т. косинусов:
в ∆PDC по т. косинусов:
(по свойству четырехугольника, вписанного в окружность).
Приравнивая эти выражения, получим уравнение относительно cos∠PQC:
Подставив обратно в любое из выражений, найдем PC:
9
Слайд 15
В окружности проведены хорды PQ и CD, причем PQ = PD
Решение. (2 случай)
в ∆PQC по т. косинусов:
в ∆PDC по т. косинусов:
(по свойству вписанных углов в окружность).
Приравнивая эти выражения, получим уравнение относительно cos∠PQC
Подставив обратно в любое из выражений, найдем PC:
9
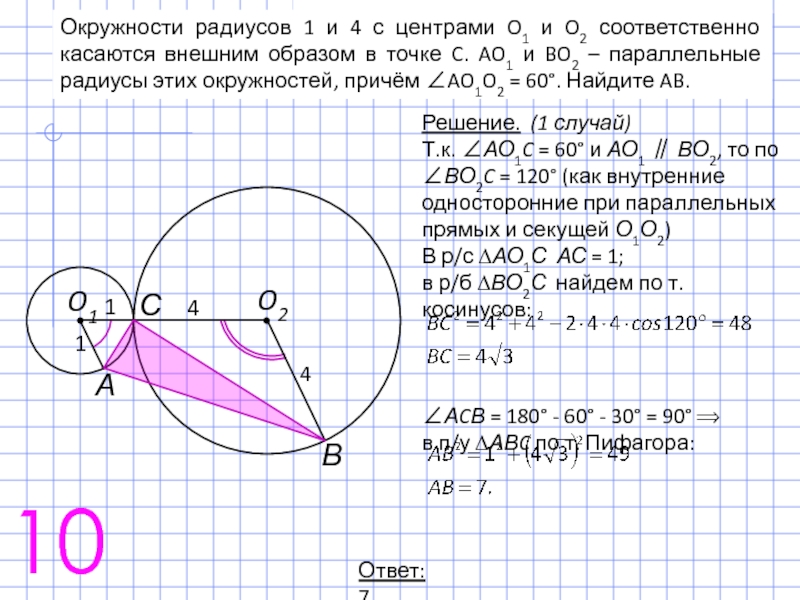
Слайд 16Окружности радиусов 1 и 4 с центрами O1 и O2 соответственно
Решение. (1 случай)
Т.к. ∠АО1C = 60° и АО1 ∥ ВО2, то по ∠ВО2C = 120° (как внутренние односторонние при параллельных прямых и секущей О1О2)
В р/с ∆АО1С АС = 1;
в р/б ∆ВО2С найдем по т. косинусов:
∠АCВ = 180° - 60° - 30° = 90° ⟹
в п/у ∆АВC по т. Пифагора:
Ответ: 7.
10
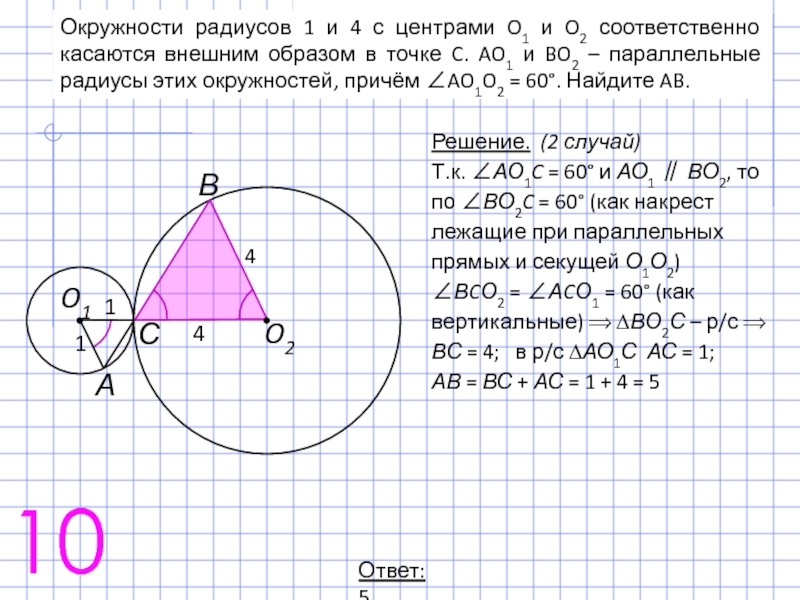
Слайд 17Окружности радиусов 1 и 4 с центрами O1 и O2 соответственно
Решение. (2 случай)
Т.к. ∠АО1C = 60° и АО1 ∥ ВО2, то по ∠ВО2C = 60° (как накрест лежащие при параллельных прямых и секущей О1О2)
∠ВCО2 = ∠АCО1 = 60° (как вертикальные) ⟹ ∆ВО2С – р/с ⟹
ВС = 4; в р/с ∆АО1С АС = 1;
АВ = ВС + АС = 1 + 4 = 5
Ответ: 5.
10
Слайд 18Решение. (1 случай)
Т.к. ∠АВО1 = 15° и ∆АО1В – р/б,
то
∠ВО1А = ∠CО2А = 180° − 2 ∙ 15°= 150°
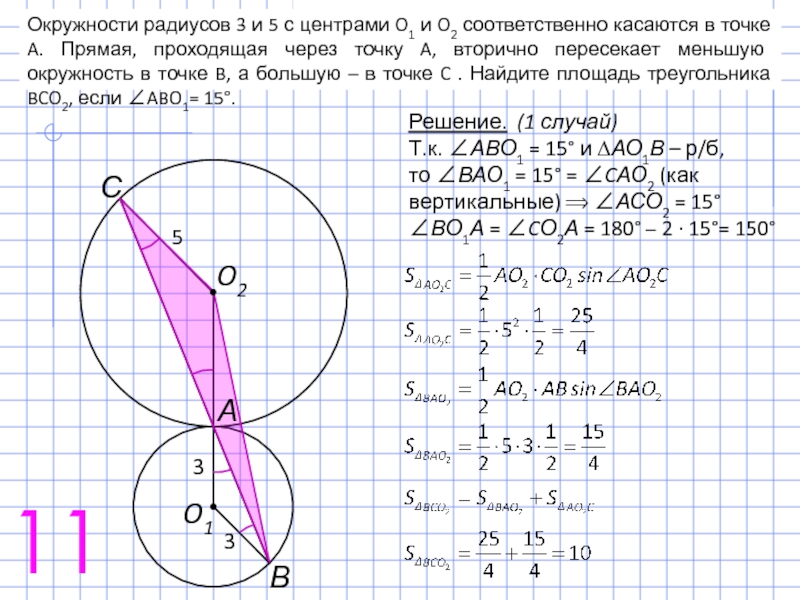
Окружности радиусов 3 и 5 с центрами O1 и O2 соответственно касаются в точке A. Прямая, проходящая через точку A, вторично пересекает меньшую окружность в точке B, а большую – в точке C . Найдите площадь треугольника BCO2, если ∠ABO1= 15°.
11
Слайд 1911
Окружности радиусов 3 и 5 с центрами O1 и O2 соответственно
Решение. (2 случай)
Т.к. ∠АВО1 = 15° и ∆АО1В – р/б,
то ∠ВАО1 = ∠АCО2 = 15° (как углы р/б ∆АО2С ) ⟹
∠ВО1А = ∠CО2А = 180° − 2 ∙ 15°= 150°
⟹
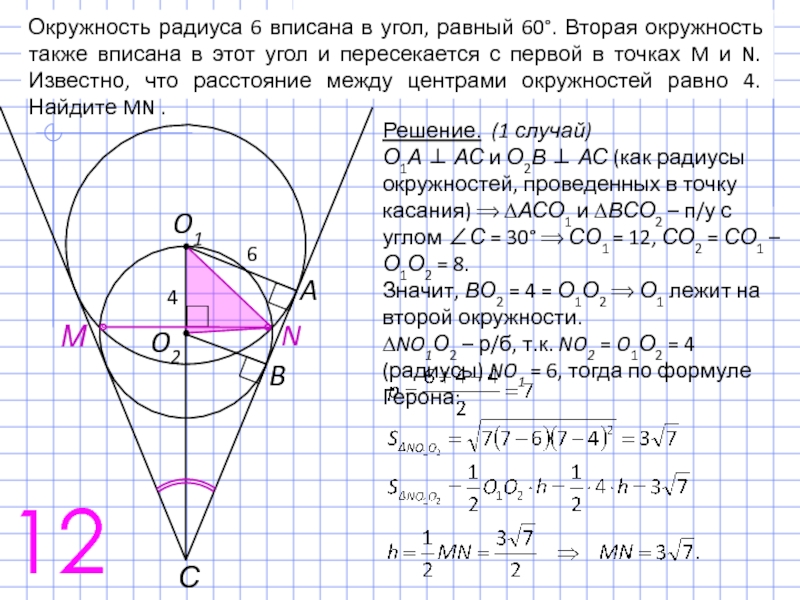
Слайд 20Окружность радиуса 6 вписана в угол, равный 60°. Вторая окружность также
Решение. (1 случай)
О1А ⊥ АС и О2В ⊥ АС (как радиусы окружностей, проведенных в точку касания) ⟹ ∆АСО1 и ∆ВСО2 – п/у с углом ∠С = 30° ⟹ СО1 = 12, СО2 = СО1 – О1О2 = 8.
Значит, ВО2 = 4 = О1О2 ⟹ О1 лежит на второй окружности.
∆NO1О2 – р/б, т.к. NO2 = O1О2 = 4 (радиусы) NO1 = 6, тогда по формуле Герона:
12
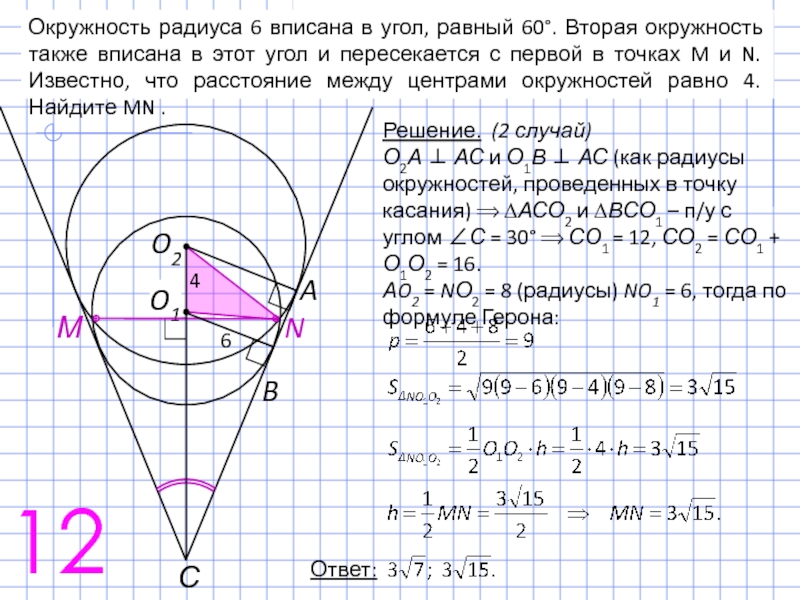
Слайд 21Окружность радиуса 6 вписана в угол, равный 60°. Вторая окружность также
Решение. (2 случай)
О2А ⊥ АС и О1В ⊥ АС (как радиусы окружностей, проведенных в точку касания) ⟹ ∆АСО2 и ∆ВСО1 – п/у с углом ∠С = 30° ⟹ СО1 = 12, СО2 = СО1 + О1О2 = 16.
АO2 = NО2 = 8 (радиусы) NO1 = 6, тогда по формуле Герона:
12
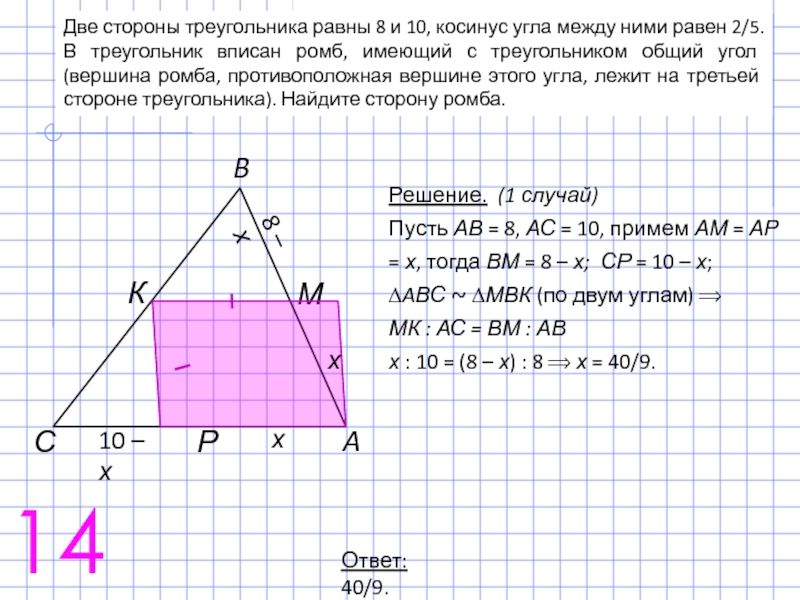
Слайд 23Две стороны треугольника равны 8 и 10, косинус угла между ними
14
Решение. (1 случай)
Пусть АВ = 8, АС = 10, примем АМ = АР = х, тогда ВМ = 8 – х; СР = 10 – х;
∆AВС ~ ∆МВК (по двум углам) ⟹
МК : АС = ВМ : АВ
х : 10 = (8 – х) : 8 ⟹ х = 40/9.
Ответ: 40/9.
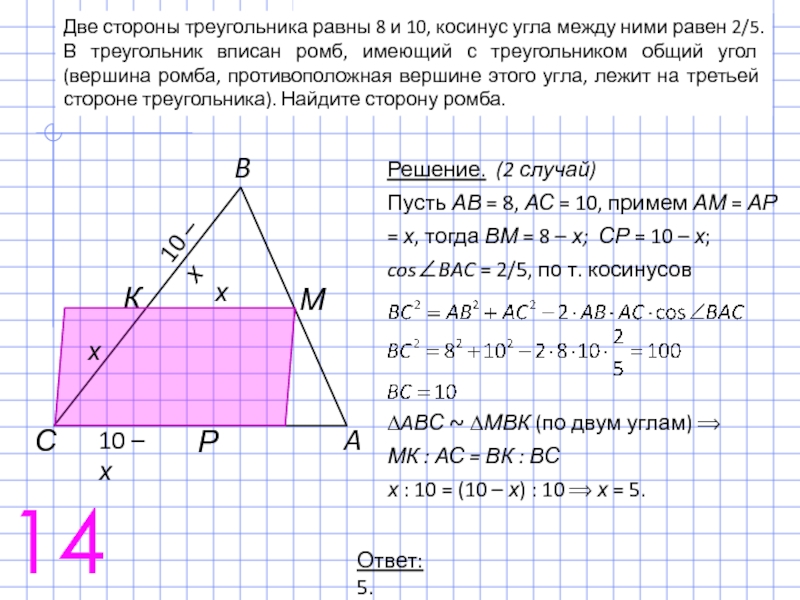
Слайд 24Две стороны треугольника равны 8 и 10, косинус угла между ними
14
Ответ: 5.
Слайд 25Расстояния от точки M, расположенной внутри прямого угла, до сторон угла
Решение.
Пусть ВК = х, АР = у, тогда АС = 4 + у; СВ = 3 + х.
∆ВКМ ~ ∆МРА (по двум углам) ⟹ ВК : МР = КМ : РА, х : 3 = 4 : у ⟹ ху = 12.
Получим систему:
⟹
По т. Пифагора в п/у ∆АВС:
15
Слайд 26Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней
Решение.
Пусть АВ = х, АС = у, тогда Р∆АВС = АВ + АС + ВС = х + у + 11;
MN = 5,5 (как средняя линия ∆АВС).
MNCB – трапеция, в которую вписана окружность ⟹
MN + BC = MB + CN = ½ (x + y) = 5,5 + 11 = 16,5 ⟹ х + у = 33;
P ∆АВС = 33 + 11 = 44.
По формуле Герона:
Получим систему:
Ответ: 13 или 20.
16
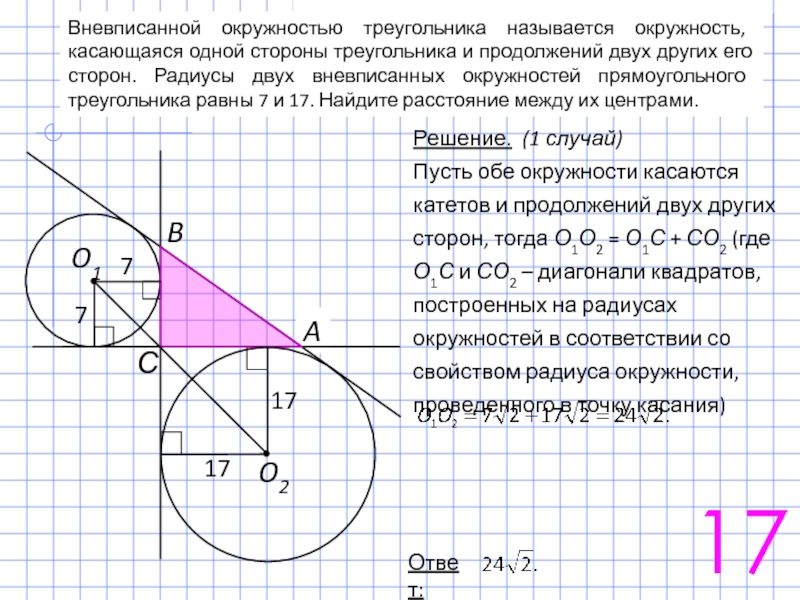
Слайд 27Вневписанной окружностью треугольника называется окружность, касающаяся одной стороны треугольника и продолжений
Решение. (1 случай)
Пусть обе окружности касаются катетов и продолжений двух других сторон, тогда О1О2 = О1С + СО2 (где О1С и СО2 – диагонали квадратов, построенных на радиусах окружностей в соответствии со свойством радиуса окружности, проведенного в точку касания)
17
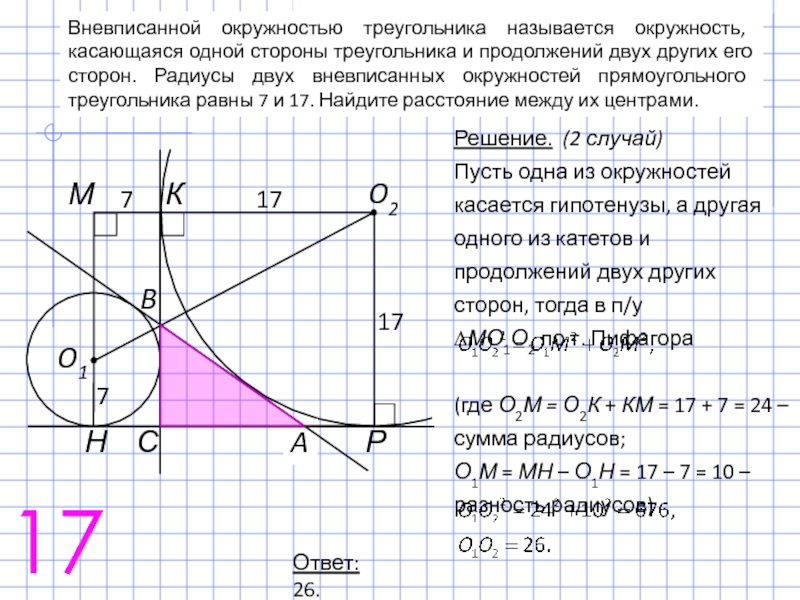
Слайд 28Вневписанной окружностью треугольника называется окружность, касающаяся одной стороны треугольника и продолжений
17
Решение. (2 случай)
Пусть одна из окружностей касается гипотенузы, а другая одного из катетов и продолжений двух других сторон, тогда в п/у
∆МО1О2 по т. Пифагора
(где О2М = О2К + КМ = 17 + 7 = 24 – сумма радиусов;
О1М = МН – О1Н = 17 – 7 = 10 – разность радиусов)
Ответ: 26.
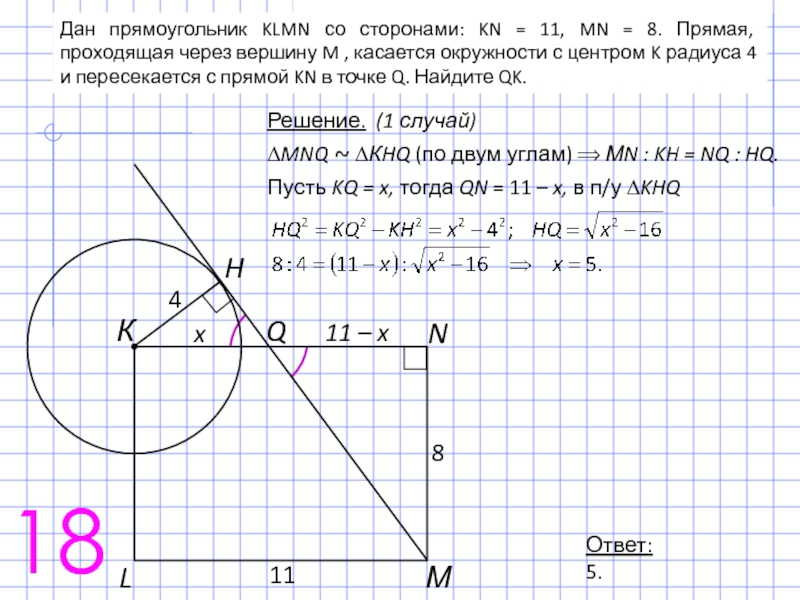
Слайд 29Дан прямоугольник KLMN со сторонами: KN = 11, MN = 8.
Решение. (1 случай)
∆MNQ ~ ∆КHQ (по двум углам) ⟹ МN : KH = NQ : HQ. Пусть KQ = x, тогда QN = 11 – x, в п/у ∆KHQ
Ответ: 5.
18
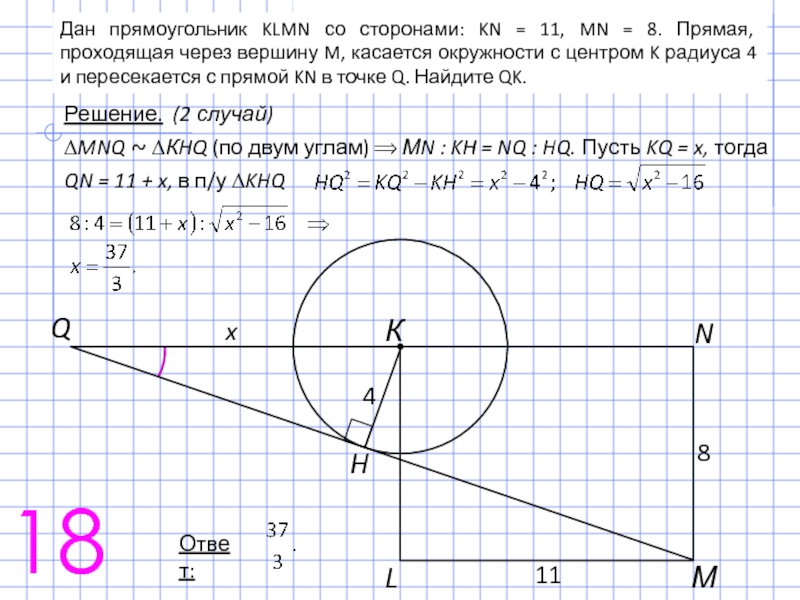
Слайд 30Дан прямоугольник KLMN со сторонами: KN = 11, MN = 8.
Решение. (2 случай)
∆MNQ ~ ∆КHQ (по двум углам) ⟹ МN : KH = NQ : HQ. Пусть KQ = x, тогда
QN = 11 + x, в п/у ∆KHQ
18
Слайд 31Боковые стороны KL и MN трапеции KLMN равны 10 и 26
19
Решение. (1 случай)
BC = 24, EF = 12, значит СЕ = BF = (24 – 12) : 2 = 6 (как средние линии ∆KLM и ∆NLM) ⟹ LM = 12;
KN = 2(CE + EF) = 2(6 + 12) = 36 (CF – средняя линия ∆KLN)
∆AKN ~ ∆ALM (по двум углам) ⟹ AL : AK = LM : KN = AM : AN.
Пусть AL = x, AM = y, тогда AK = 10 + x,
AN = 26 + y.
x : (10 + x) = 12 : 36 ⟹ x = 5;
y : (26 + y) = 12 : 36 ⟹ y = 13.
Значит, ∆AKN ~ ∆ALM – п/у.
Ответ: 2.
Слайд 32Боковые стороны KL и MN трапеции KLMN равны 10 и 26
19
Решение. (2 случай)
BC = 24, EF = 12, значит СЕ = BF = (24 – 12) : 2 = 6 (как средние линии ∆KLM и ∆NLM) ⟹ LM = 12;
KN = 2(CE + EF) = 2(6 + 12) = 36 (CF – средняя линия ∆KLN)
∆AKN ~ ∆ALM (по двум углам) ⟹ AL : AK = LM : KN = AM : AN.
Пусть AL = x, AM = y, тогда AK = 10 + x,
AN = 26 + y.
x : (10 + x) = 12 : 36 ⟹ x = 5;
y : (26 + y) = 12 : 36 ⟹ y = 13.
Значит, ∆AKN ~ ∆ALM – п/у.
AL = AK + KL = 5 + 10 = 15.
Ответ: 6.
x
y
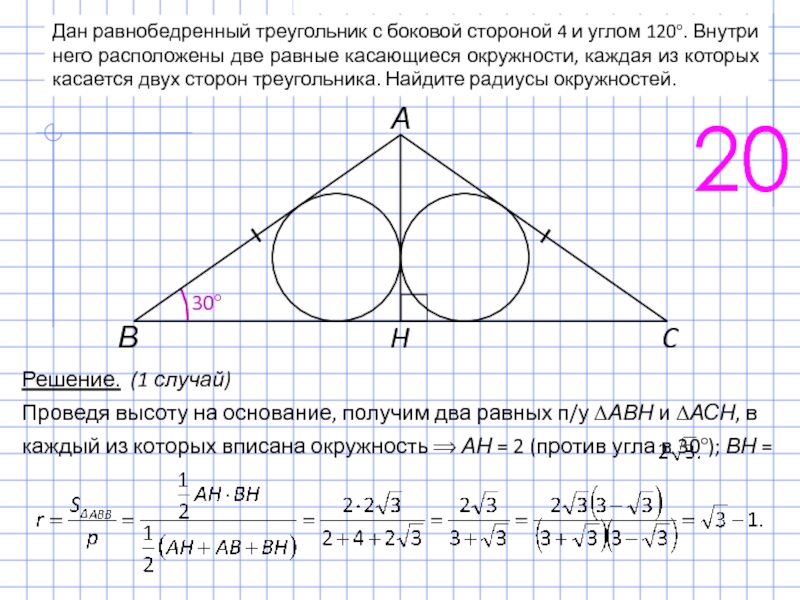
Слайд 33Дан равнобедренный треугольник с боковой стороной 4 и углом 120°. Внутри
20
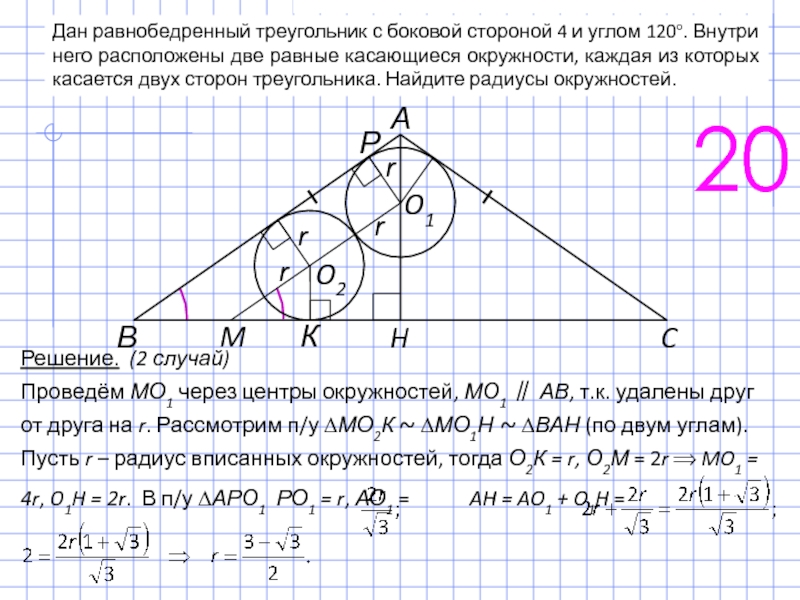
Слайд 34Дан равнобедренный треугольник с боковой стороной 4 и углом 120°. Внутри
Слайд 35В треугольнике ABC известны стороны: AB = 5, BC = 6,
Решение. (1 случай)
∠ВАС + ∠KLC = 180° (по свойству трапеции, вписанной в окружность), ∠KLC = 180° − ∠ВАС ⟹
∠BLK = 180° − ∠KLС = ∠ВАС.
Аналогично, ∠ВKL = ∠ВСА ⟹
∆ВАС ~ ∆ВLK ⟹
BK : BC = BL : BA = KL : AC
BK : 6 = BL : 5 = KL : 7
KL + AC = AK + LC (по свойству трапеции,
описанной около окружности). Пусть BK = x, BL = y, тогда АК = 5 – х, BL = 6 – y.
21
Слайд 36Решение. (1 случай)
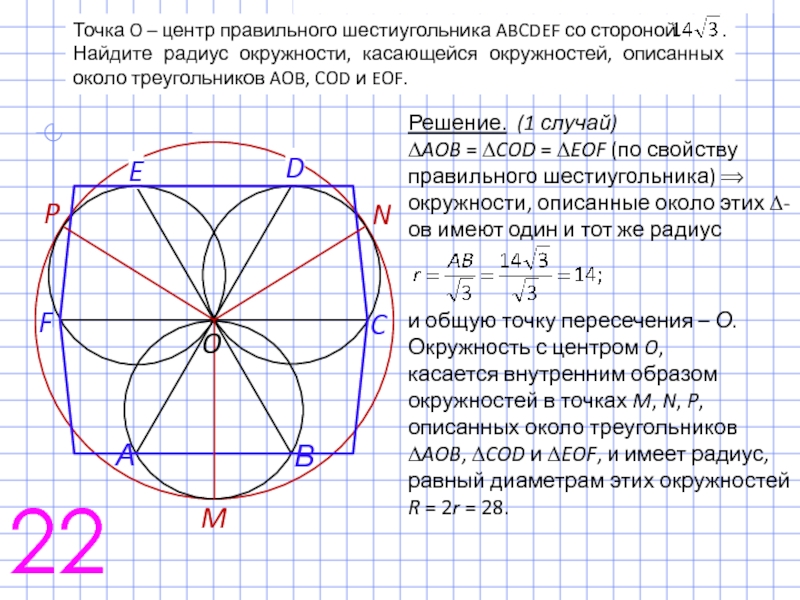
∆AOB = ∆COD = ∆EOF (по свойству правильного шестиугольника)
окружности, описанные около этих ∆-ов имеют один и тот же радиус
и общую точку пересечения – О.
Окружность с центром O,
касается внутренним образом окружностей в точках M, N, P, описанных около треугольников ∆AOB, ∆COD и ∆EOF, и имеет радиус, равный диаметрам этих окружностей
R = 2r = 28.
22
Слайд 37Решение. (2 случай)
∆AOB = ∆COD = ∆EOF = ∆O2О3О4
Окружность с центром
касается внутренним образом одной окружности в точке M и внешним образом двух других окружностей, описанных около треугольников ∆COD и ∆EOF.
Пусть радиус этой окружности – r1.
По т. Пифагора в п/у ∆КO1О3
22
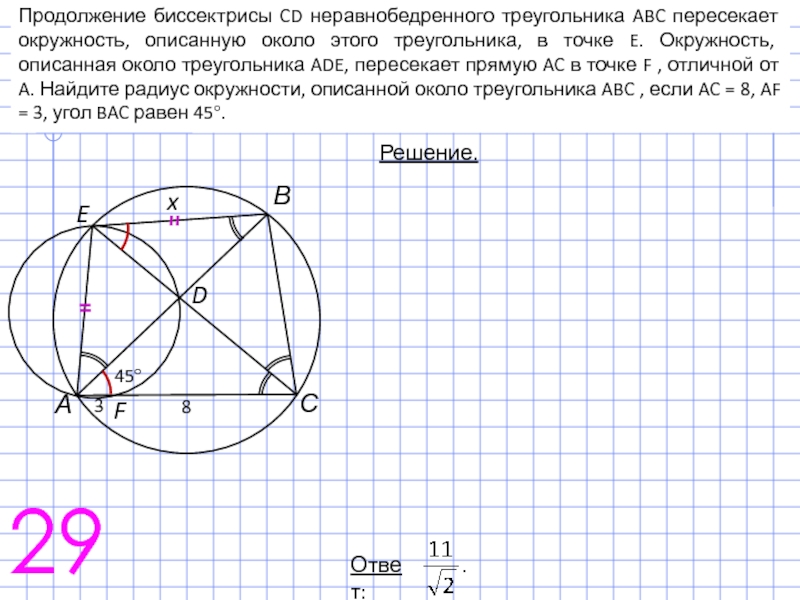
Слайд 38Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого
23
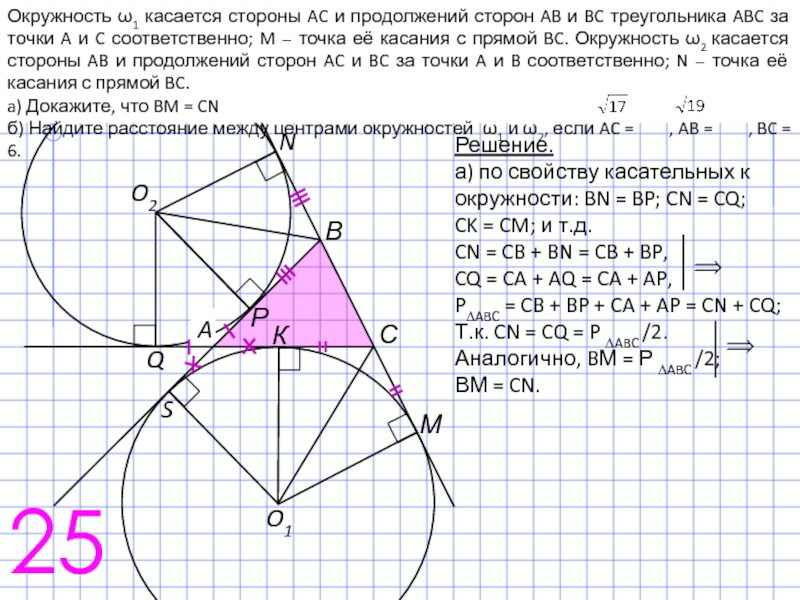
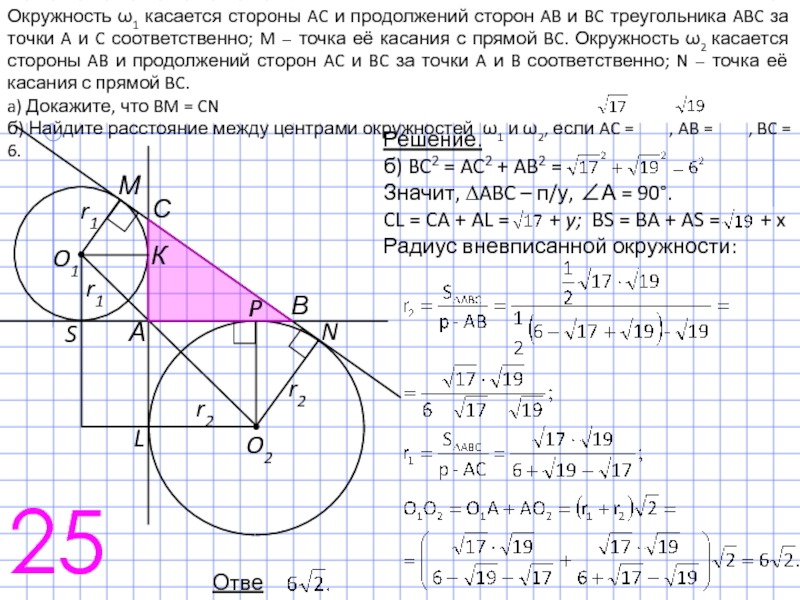
Слайд 4025
Решение.
а) по свойству касательных к окружности: BN = BP; CN =
CK = CM; и т.д.
CN = CB + BN = CB + BP,
CQ = CA + AQ = CA + AP,
P∆ABC = CB + BP + CA + AP = CN + CQ;
Т.к. CN = CQ = P ∆ABC /2.
Аналогично, BМ = Р ∆ABC /2;
ВМ = CN.
⟹
⟹
S
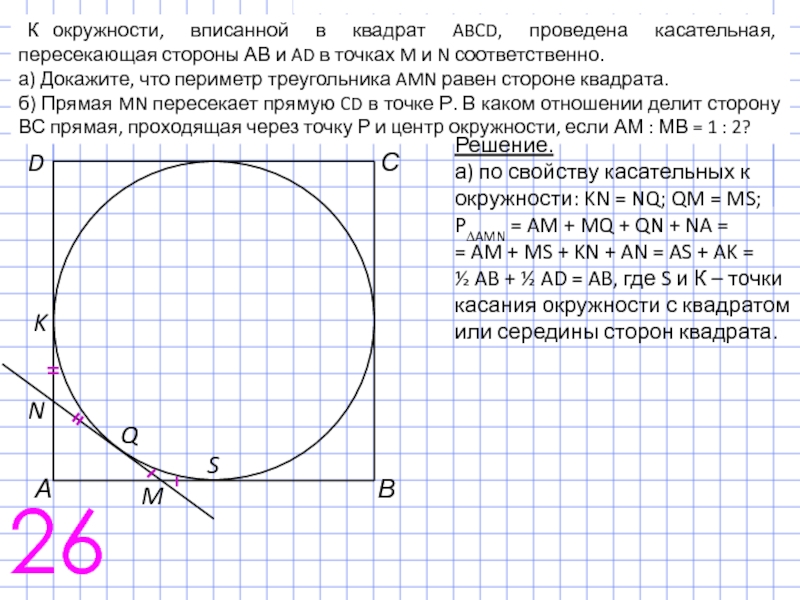
Слайд 42 К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке Р. В каком отношении делит сторону ВС прямая, проходящая через точку Р и центр окружности, если АМ : МВ = 1 : 2?
26
Решение.
а) по свойству касательных к окружности: KN = NQ; QM = MS;
P∆AMN = AM + MQ + QN + NA =
= AM + MS + KN + AN = AS + AK =
½ AB + ½ AD = AB, где S и К – точки касания окружности с квадратом или середины сторон квадрата.
Слайд 43К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны АВ
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке Р. В каком отношении делит сторону ВС прямая, проходящая через точку Р и центр окружности, если АМ : МВ = 1 : 2?
26
Решение.
б) Пусть сторона квадрата = 3х, AN = y.
Тогда AM = x, и MN = P∆AMN – x – y =
= 3x – x – y = 2x – y.
Радиус вневписанной окружности OE:
Откуда y = 0,75x, DN = 3x – 0,75x = 2,25x.
∆AMN ~ ∆DPN (по углам) ⟹
АM : DР = AN : DN; x : DP = 0,75x : 2,25x,
DP = 3x, EP = 4,5x, CP = 6x.
∆OEP ~ ∆LCP (по углам) ⟹
OE : CL = EP : CP; 1,5x : CL = 4,5x : 6x,
CL = 2x, LB = 3x – 2x = x ⟹ CL : BL = 2 : 1.
Слайд 44
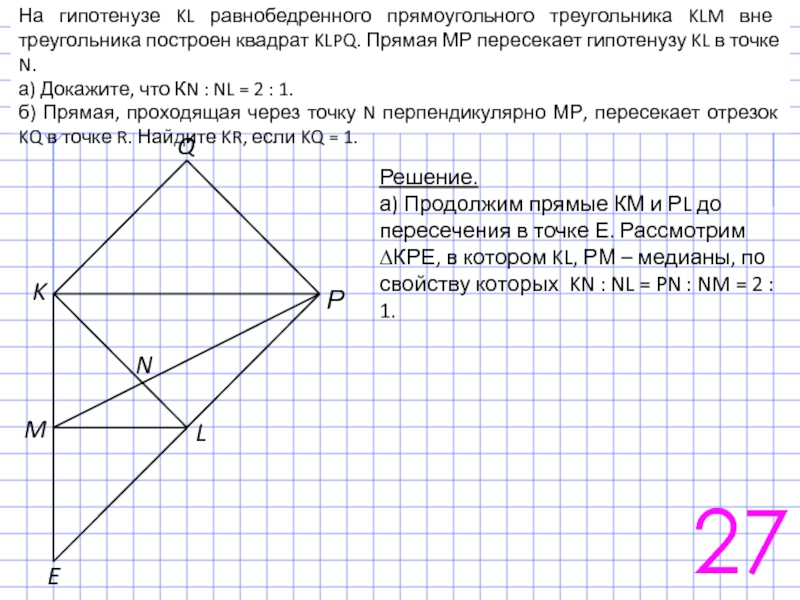
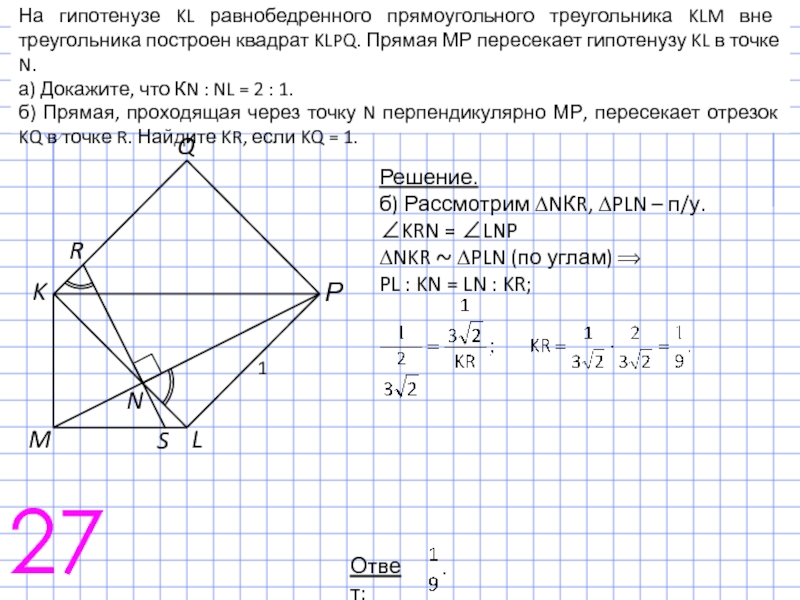
На гипотенузе KL равнобедренного прямоугольного треугольника KLM вне треугольника построен квадрат
а) Докажите, что КN : NL = 2 : 1.
б) Прямая, проходящая через точку N перпендикулярно МР, пересекает отрезок KQ в точке R. Найдите KR, если KQ = 1.
27
Решение.
а) Продолжим прямые КМ и РL до пересечения в точке Е. Рассмотрим ∆КРЕ, в котором KL, РМ – медианы, по свойству которых KN : NL = PN : NM = 2 : 1.
Q
N
M
Р
L
K
E
Слайд 45На гипотенузе KL равнобедренного прямоугольного треугольника KLM вне треугольника построен квадрат
а) Докажите, что КN : NL = 2 : 1.
б) Прямая, проходящая через точку N перпендикулярно МР, пересекает отрезок KQ в точке R. Найдите KR, если KQ = 1.
27
Решение.
б) Рассмотрим ∆NКR, ∆PLN – п/у.
∠KRN = ∠LNP
∆NKR ~ ∆PLN (по углам) ⟹
PL : KN = LN : KR;
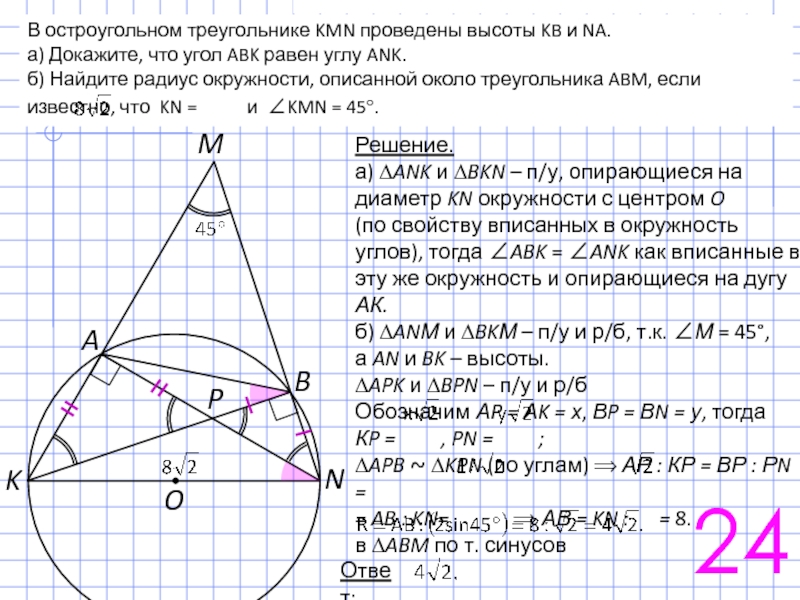
Слайд 47Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого
29
Решение.
С
F
А
В
E
x
8
D
45°
3
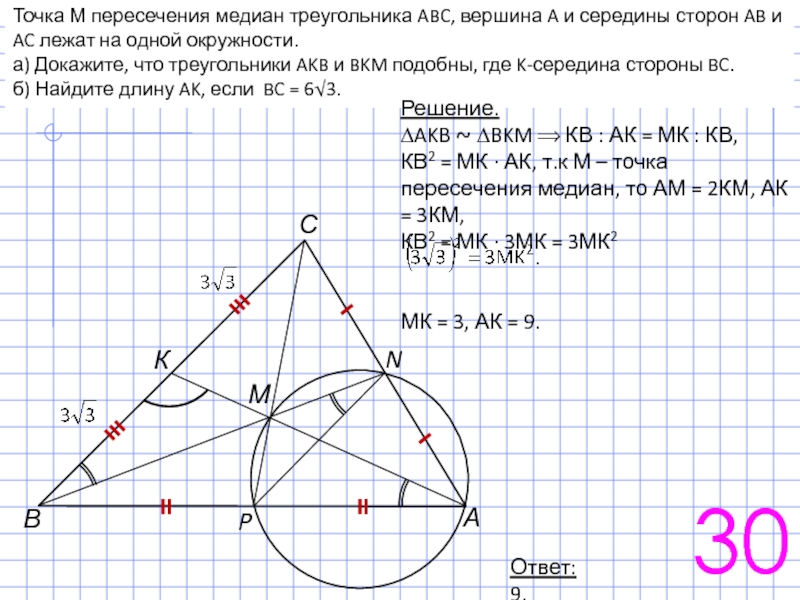
Слайд 4830
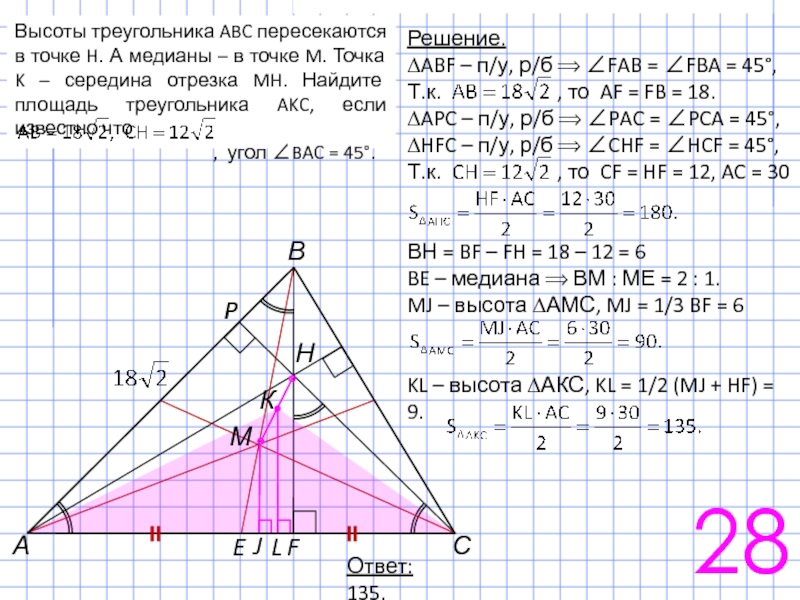
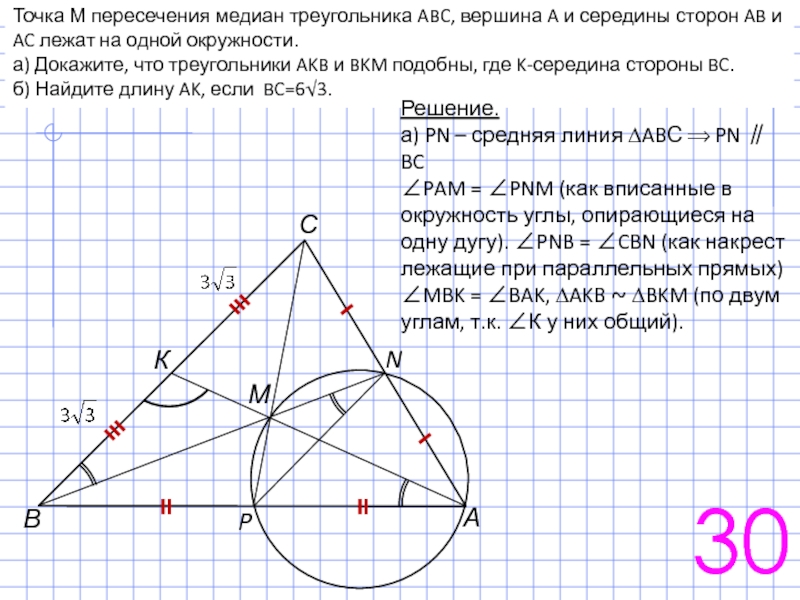
Точка М пересечения медиан треугольника ABC, вершина A и середины сторон
а) Докажите, что треугольники AKB и BKM подобны, где K-середина стороны BC.
б) Найдите длину AK, если BC=6√3.
Решение.
а) PN – средняя линия ∆ABС ⟹ PN ∥ BC
∠PAM = ∠PNM (как вписанные в окружность углы, опирающиеся на одну дугу). ∠PNB = ∠CBN (как накрест лежащие при параллельных прямых)
∠MBK = ∠BAK, ∆AKB ~ ∆BKM (по двум углам, т.к. ∠К у них общий).
Слайд 4930
Точка М пересечения медиан треугольника ABC, вершина A и середины сторон
а) Докажите, что треугольники AKB и BKM подобны, где K-середина стороны BC.
б) Найдите длину AK, если BC = 6√3.
Решение.
∆AKB ~ ∆BKM ⟹ КВ : АК = МК : КВ,
КВ2 = МК ∙ АК, т.к М – точка пересечения медиан, то АМ = 2КМ, АК = 3КМ,
КВ2 = МК ∙ 3МК = 3МК2
МК = 3, АК = 9.
Ответ: 9.