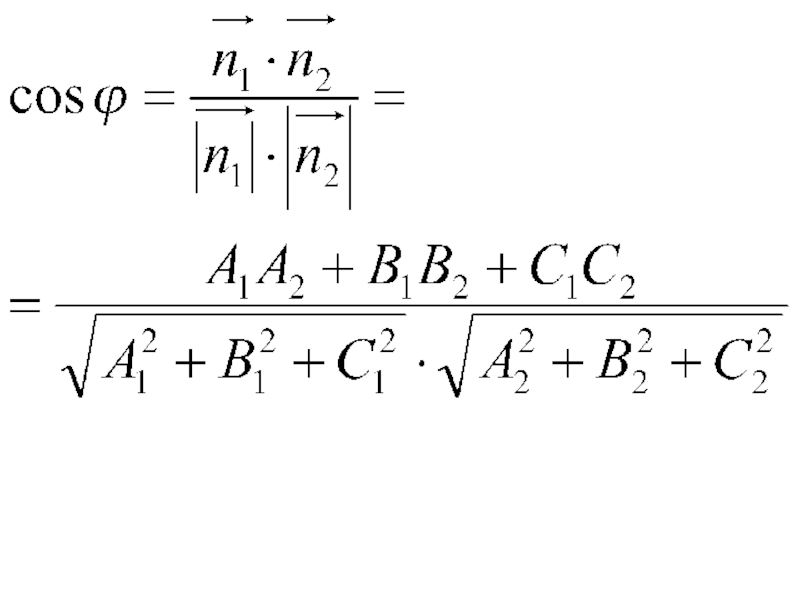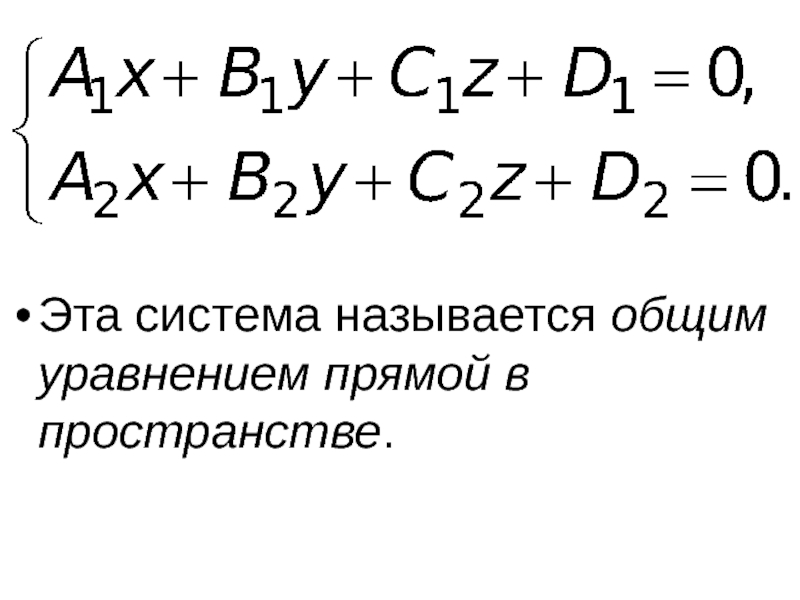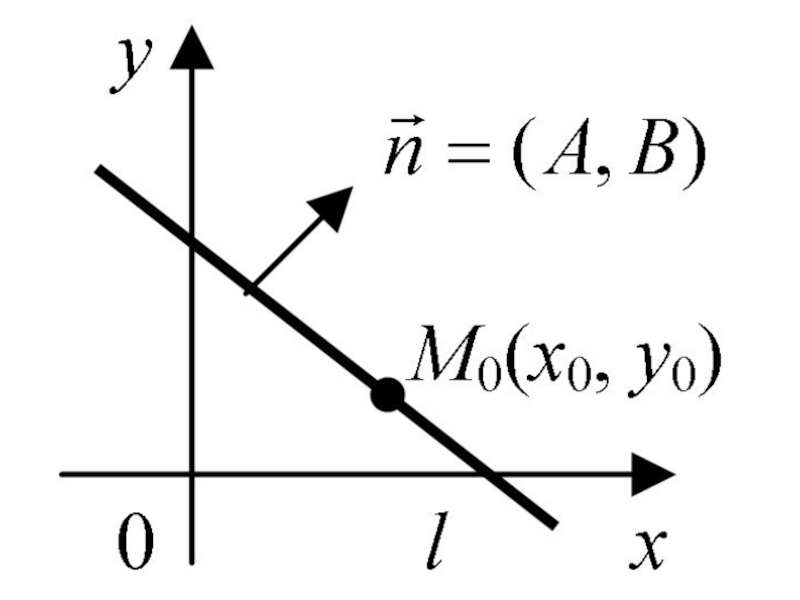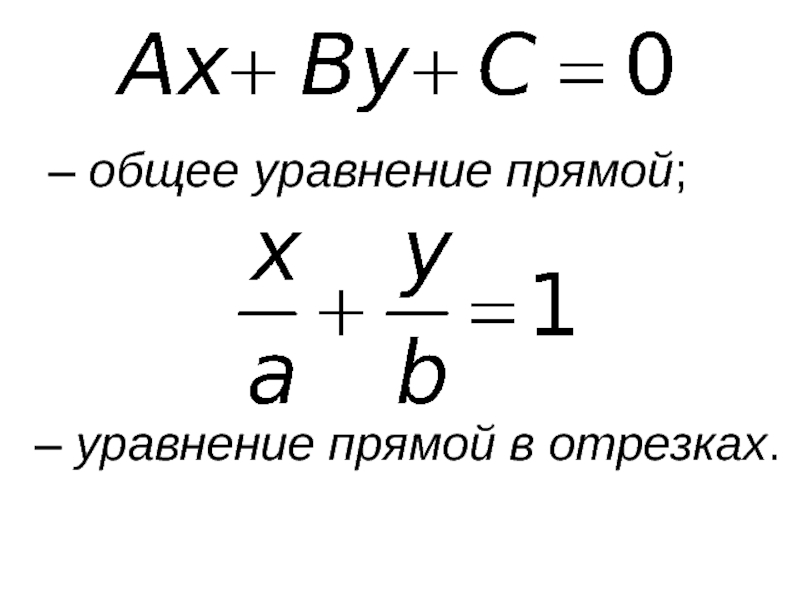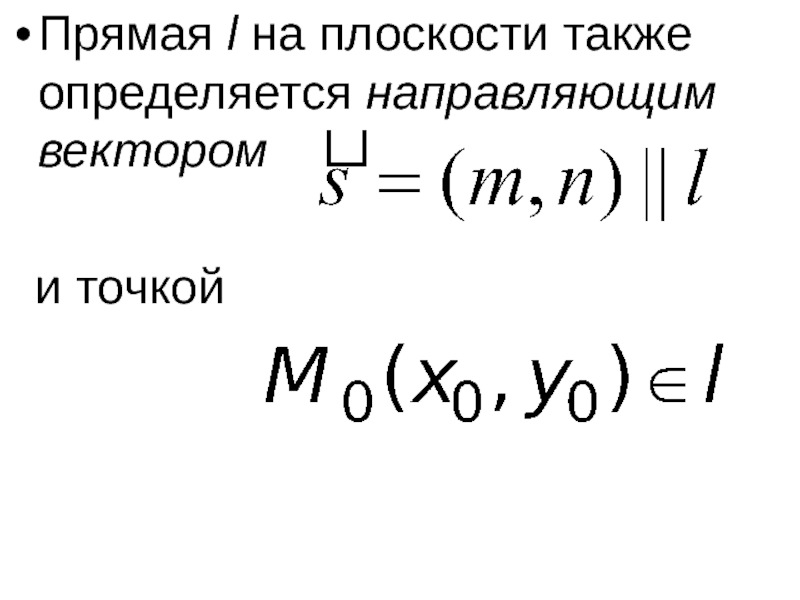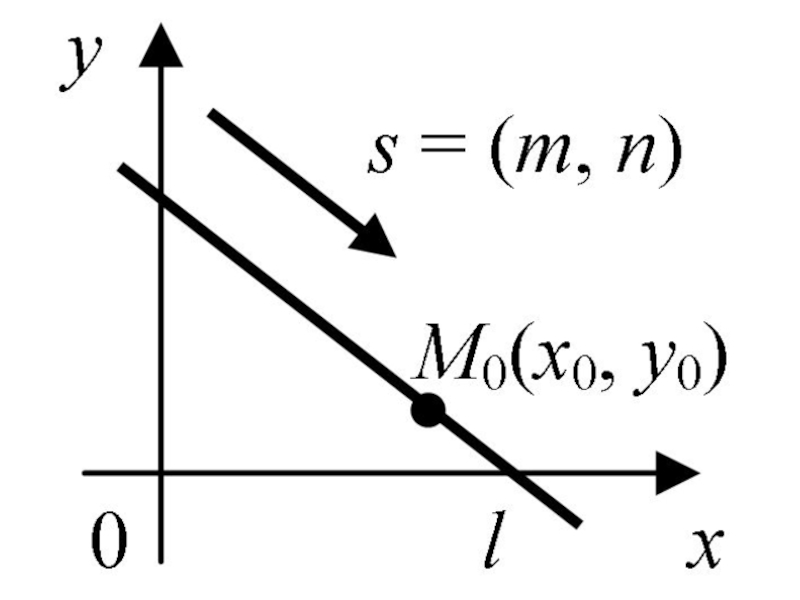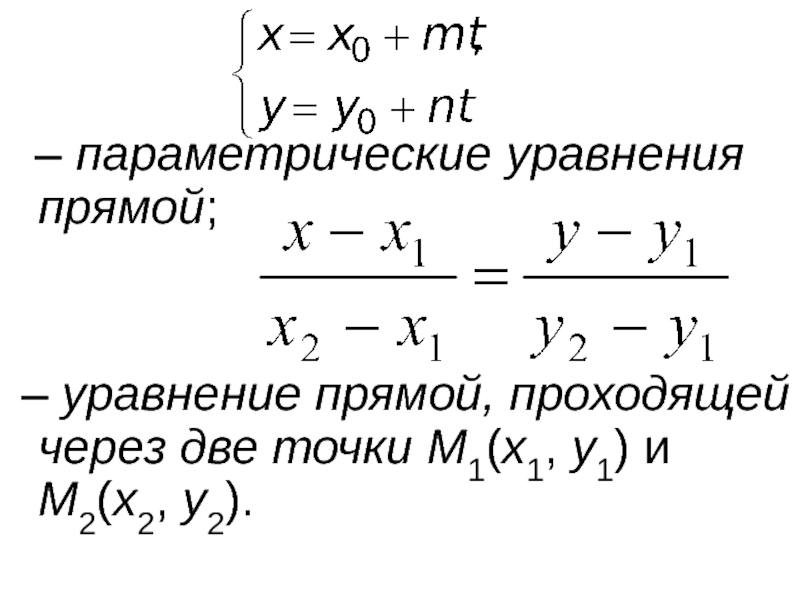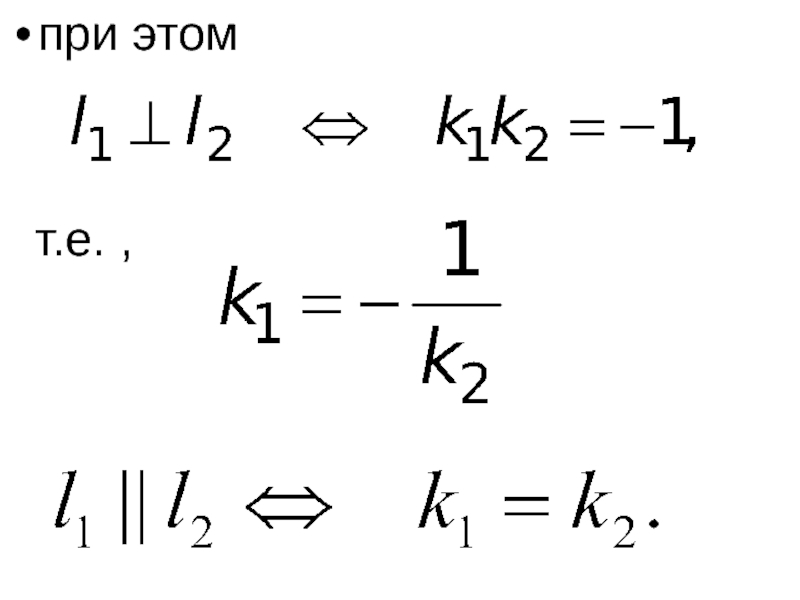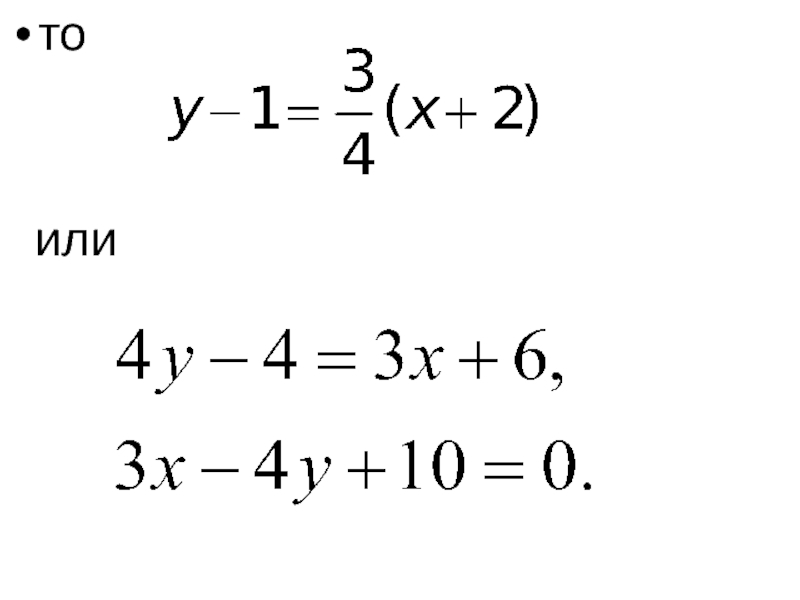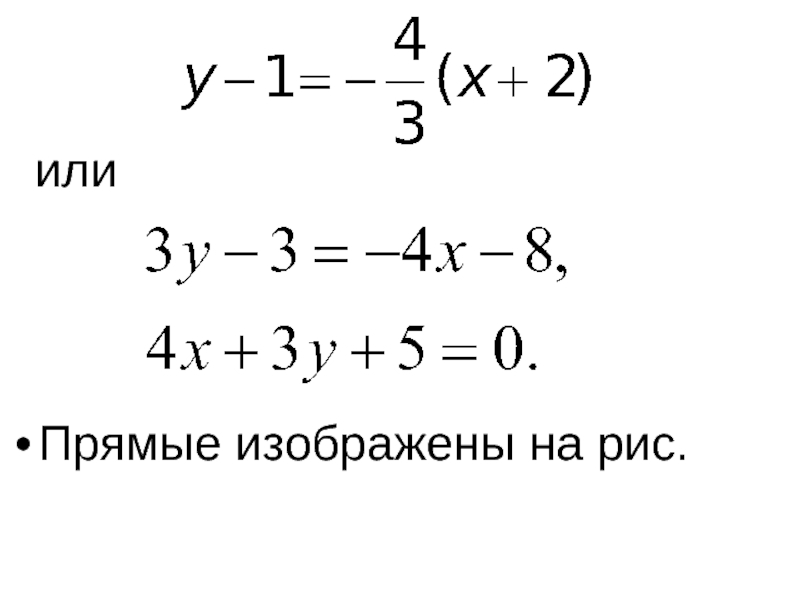- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналитическая геометрия презентация
Содержание
- 1. Аналитическая геометрия
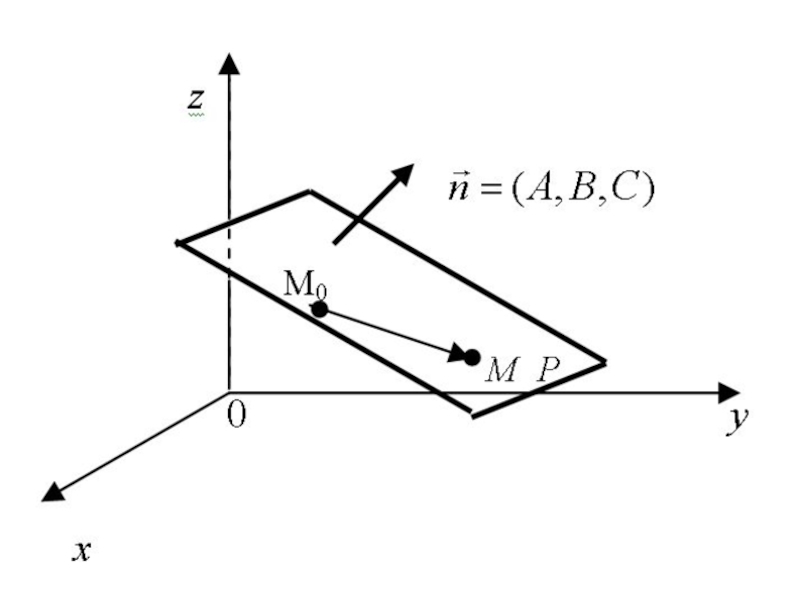
- 2. Плоскость и её основные уравнения Рассмотрим
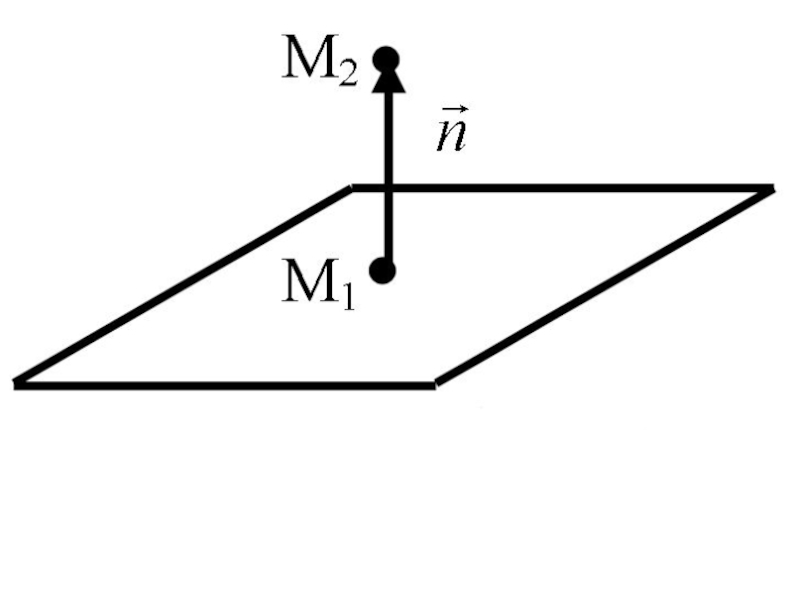
- 3. Положение плоскости вполне определяется точкой и вектором нормали
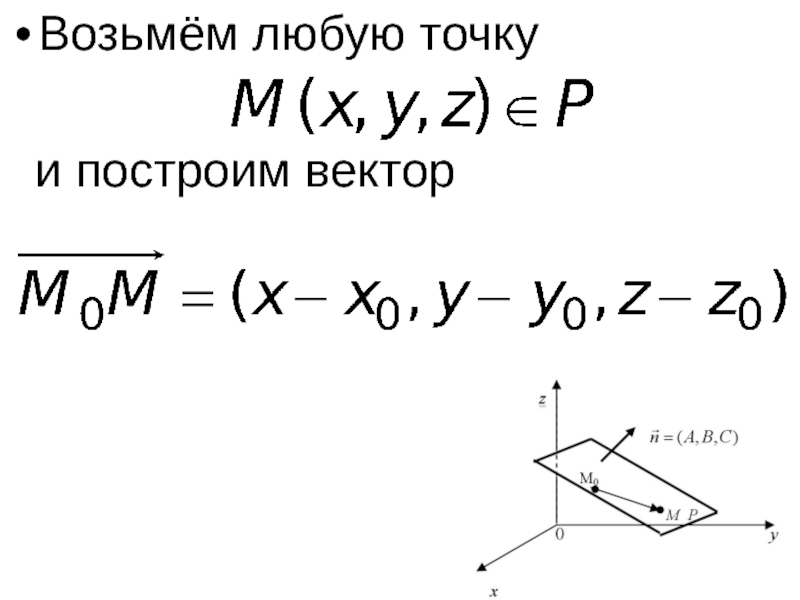
- 5. Возьмём любую точку и построим вектор
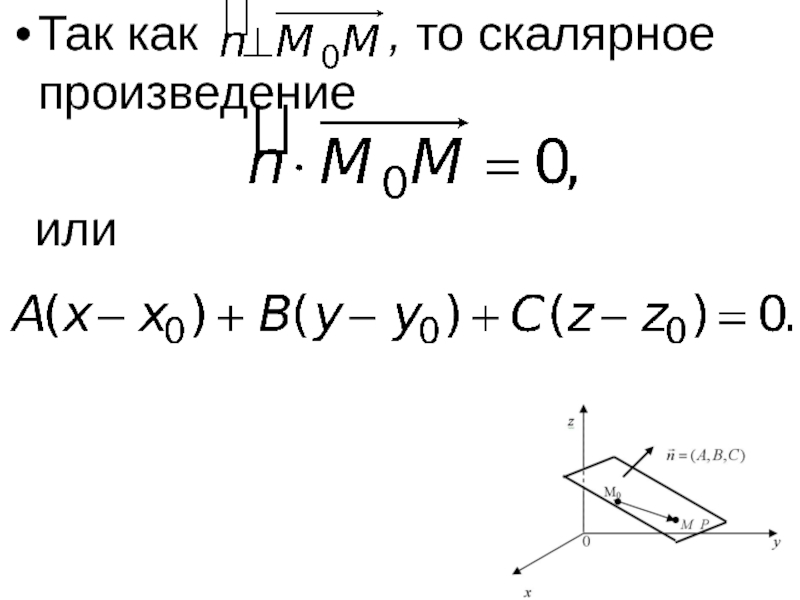
- 6. Так как
- 7. Получили уравнение плоскости, заданной точкой
- 8. Если в уравнении раскрыть
- 9. Теорема. Всякое уравнение вида определяет некоторую плоскость в пространстве.
- 10. Если в этом уравнении какой-либо из коэффициентов
- 11. Например, при A = 0 плоскость By
- 12. Пусть в уравнении ни
- 13. Получим уравнение плоскости в отрезках:
- 14. где a, b, c – это величины направленных отрезков, отсекаемых плоскостью на осях координат
- 16. Если три точки
- 18. Уравнение плоскости, проходящей через три точки, имеет вид:
- 19. Пусть даны две плоскости и
- 21. Расстояние d от точки
- 22. Пример. Даны две точки
- 23. Решение. Поскольку искомая плоскость перпендикулярна вектору
- 25. Подставив теперь в уравнение
- 26. или
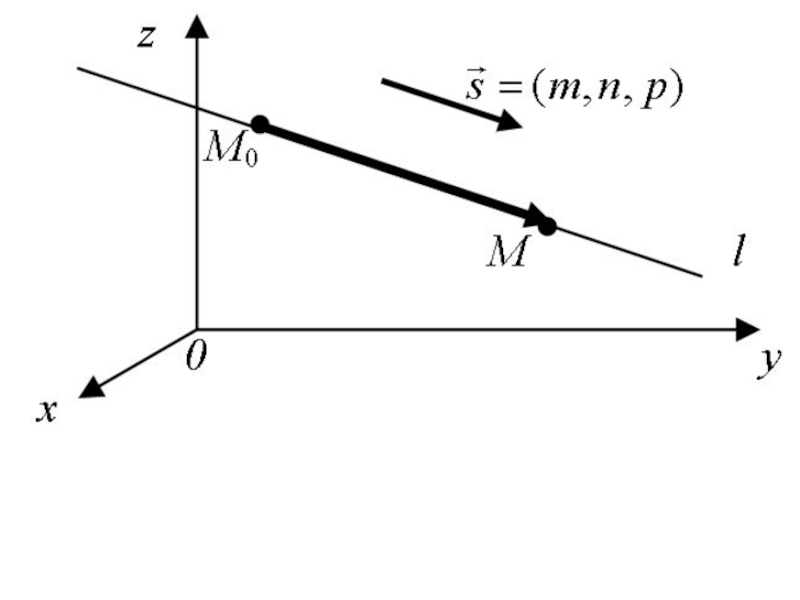
- 27. Прямая в пространстве и её основные уравнения
- 29. Возьмем любую точку
- 30. Обозначим коэффициент пропорциональности через параметр t и
- 31. Уравнение прямой, проходящей через две точки M1(x1,
- 32. Рассмотрим две плоскости P1 : A1x +
- 33. Эта система называется общим уравнением прямой в пространстве.
- 34. Угол φ между двумя прямыми l1 и
- 35. Угол ψ между прямой
- 36. Пример. Составить канонические и параметрические уравнения прямой,
- 37. Решение. Подставляем в формулу координаты точек M1(3;
- 38. или –
- 39. Запишем параметрические уравнения прямой:
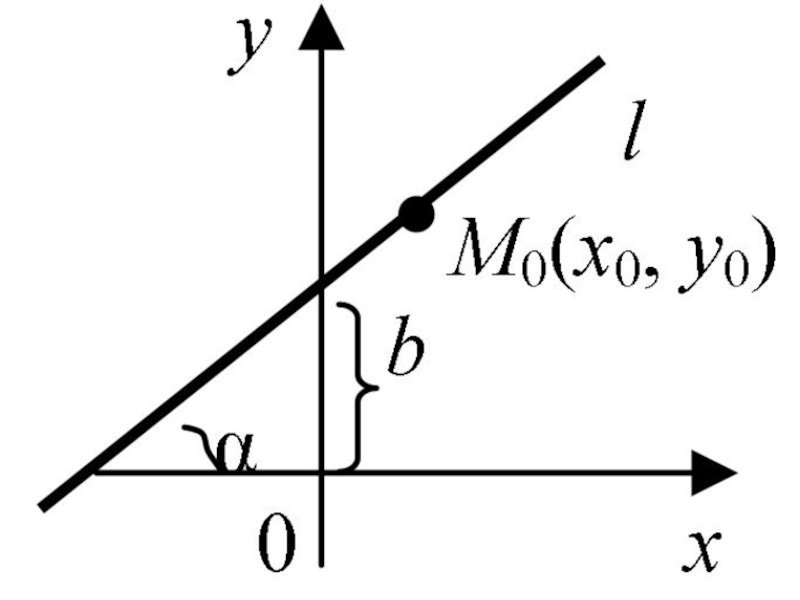
- 40. Прямая на плоскости и её основные уравнения
- 41. где k = tg α –
- 43. Кроме того, прямую l на плоскости можно
- 45. Получим три уравнения, аналогичные уравнениям для плоскости:
- 46. – общее уравнение
- 47. Прямая l на плоскости также определяется направляющим
- 49. Получим еще 3 уравнения, аналогичные уравнениям прямой
- 50. – параметрические уравнения прямой;
- 51. Угол между двумя прямыми, заданными уравнениями:
- 52. при этом т.е. ,
- 53. Расстояние d от точки M1(x1, y1) до
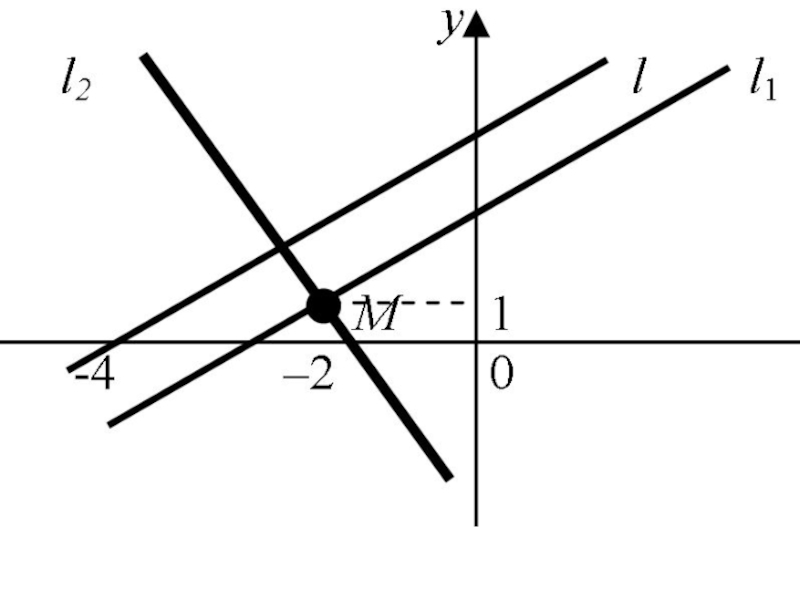
- 54. Пример. Записать уравнения прямых, проходящих через
- 55. Решение. Перепишем общее уравнение прямой 3x –
- 56. Получили уравнение прямой с угловым коэффициентом k
- 57. то или
- 58. Составим уравнение прямой
- 59. или Прямые изображены на рис.
Плоскость и её основные уравнения Рассмотрим плоскость P в прямоугольной декартовой системе координат.
Слайд 2Плоскость и её основные уравнения
Рассмотрим плоскость P в прямоугольной декартовой
системе координат.
Слайд 10Если в этом уравнении какой-либо из коэффициентов A, B, C равен
нулю, то плоскость расположена параллельно той оси, координата которой отсутствует в уравнении.
Слайд 11Например, при A = 0 плоскость By + Cz + D
= 0 параллельна оси Ox; при A = B = 0 плоскость Cz + D = 0 параллельна осям Ox и Oy, т.е. плоскости xOy и т.д.
Слайд 12Пусть в уравнении
ни один из коэффициентов не равен 0.
Перепишем это уравнение в виде
разделим обе части этого равенства на - D и обозначим
разделим обе части этого равенства на - D и обозначим
Слайд 16Если три точки
не лежат на одной прямой, то через
эти точки проходит единственная плоскость:
Слайд 19Пусть даны две плоскости
и
Угол φ между двумя плоскостями равен
углу между их векторами нормали:
Слайд 22Пример. Даны две точки
Записать уравнение плоскости, проходящей через точку
M1 перпендикулярно вектору
Слайд 23Решение. Поскольку искомая плоскость перпендикулярна вектору
, то в качестве вектора нормали возьмем вектор
Слайд 27Прямая в пространстве и её основные уравнения
Рассмотрим прямую l в
прямоугольной декартовой системе координат. Положение прямой в пространстве вполне определяется точкой и направляющим вектором
Слайд 29Возьмем любую точку
и построим вектор , из условия коллинеарности этих векторов получим канонические уравнения прямой в пространстве:
Слайд 30Обозначим коэффициент пропорциональности через параметр t и выразим через t переменные
x, y, z. Приходим к параметрическим уравнениям прямой в пространстве:
Слайд 32Рассмотрим две плоскости P1 : A1x + B1y + C1z+ D1
= 0 и
P2 : A2x + B2y + C2z+ D2 = 0. Если эти плоскости не параллельны, то они пересекаются по прямой, задаваемой системой уравнений:
P2 : A2x + B2y + C2z+ D2 = 0. Если эти плоскости не параллельны, то они пересекаются по прямой, задаваемой системой уравнений:
Слайд 36Пример. Составить канонические и параметрические уравнения прямой, проходящей через точки M1(3;
2; -1) и M2(4; 2; 1).
Слайд 38или
– канонические уравнения прямой (нуль в знаменателе означает,
что направляющий вектор перпендикулярен оси Oy, т.е. прямая перпендикулярна оси Oy).
Слайд 40Прямая на плоскости и её основные уравнения
Уравнение прямой с угловым
коэффициентом k имеет вид
или
или
Слайд 41 где k = tg α – угловой коэффициент прямой, b
– величина отрезка, отсекаемого этой прямой на оси Oy, (x0, y0) – точка, лежащая на прямой.
Слайд 45Получим три уравнения, аналогичные уравнениям для плоскости:
– уравнение
прямой, заданной точкой и вектором нормали;
Слайд 49Получим еще 3 уравнения, аналогичные уравнениям прямой в пространстве:
– каноническое
уравнение прямой;
Слайд 50
– параметрические уравнения прямой;
– уравнение прямой, проходящей через две
точки M1(x1, y1) и M2(x2, y2).
Слайд 54Пример. Записать уравнения прямых, проходящих через точку M(– 2, 1)
параллельно и перпендикулярно прямой
3x – 4y + 12 = 0.
3x – 4y + 12 = 0.
Слайд 56Получили уравнение прямой с угловым коэффициентом k = 3/4. Запишем уравнение
прямой
и проходящей через точку M(– 2, 1). Поскольку для параллельных прямых угловые коэффициенты равны, т.е.
и проходящей через точку M(– 2, 1). Поскольку для параллельных прямых угловые коэффициенты равны, т.е.
Слайд 58Составим уравнение прямой
, проходящей через
точку M(– 2,1). Так как угловые коэффициенты перпендикулярных прямых связаны соотношением
то
то
