- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка ЕГЭ. Задания В7-2018 презентация
Содержание
- 1. Подготовка ЕГЭ. Задания В7-2018
- 2. На рисунке изображен график функции y=f(x) ,
- 3. На рисунке изображен график функции y =
- 5. На рисунке изображен график y = f
- 6. На рисунке изображен график y = f
- 7. На рисунке изображен график y = f
- 8. На рисунке изображен график y = f
- 9. На рисунке изображен график y = f
- 10. На рисунке изображен график y = f
- 11. На рисунке изображен график y = f
- 12. На рисунке изображен график y = f
- 13. На рисунке изображены график функции y=f(x) и
- 14. На рисунке изображены график функции y=f(x) и
- 15. На рисунке изображены график функции y=f(x) и
- 16. На рисунке изображен график y = f
- 17. На рисунке изображен график y = f
- 18. На рисунке изображен график функции y=f(x),
- 19. На рисунке изображён график функции y=f(x) и
- 20. На рисунке изображён график функции y=f(x) и
- 21. На рисунке изображён график y = f
На рисунке изображен график функции y=f(x) , определенной на интервале ( - 6;8) . Определите количество целых точек, в которых производная функции положительна Ответ: 4 • • • •
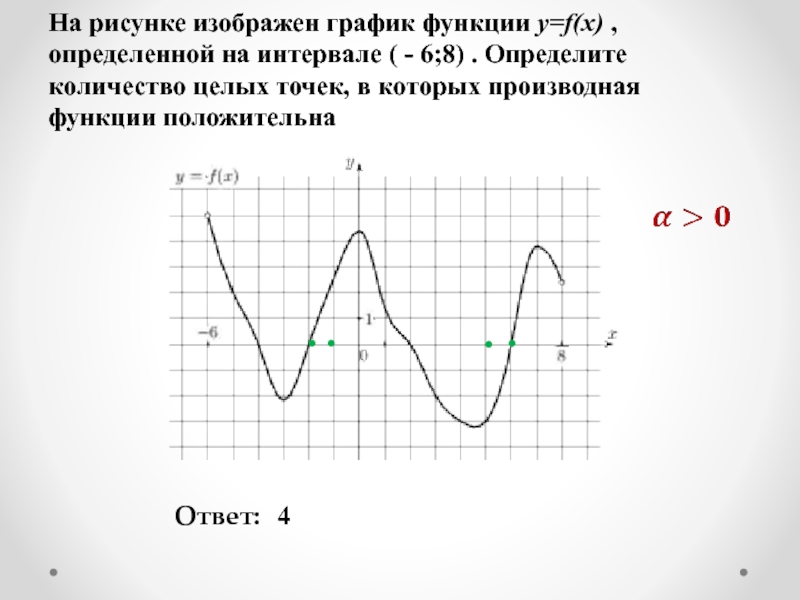
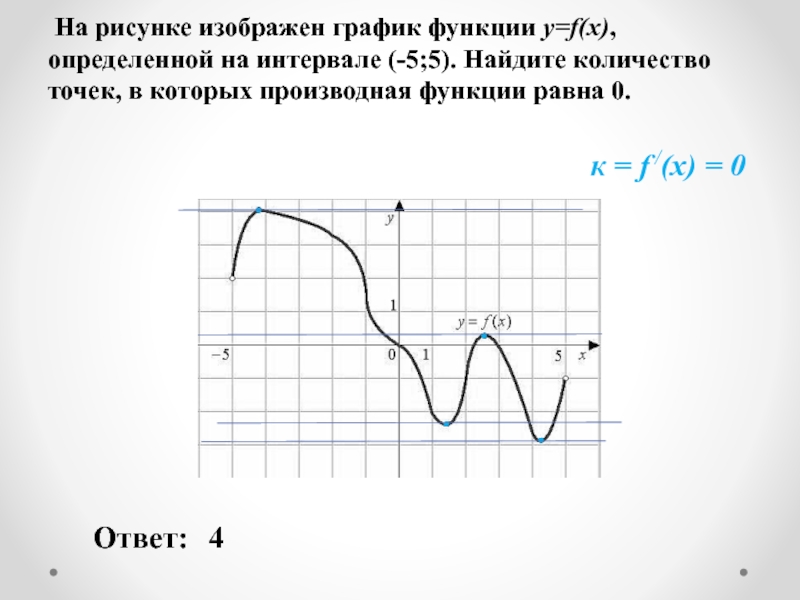
Слайд 2На рисунке изображен график функции y=f(x) , определенной на интервале (
- 6;8) . Определите количество целых точек, в которых производная функции положительна
Ответ:
4
•
•
•
•
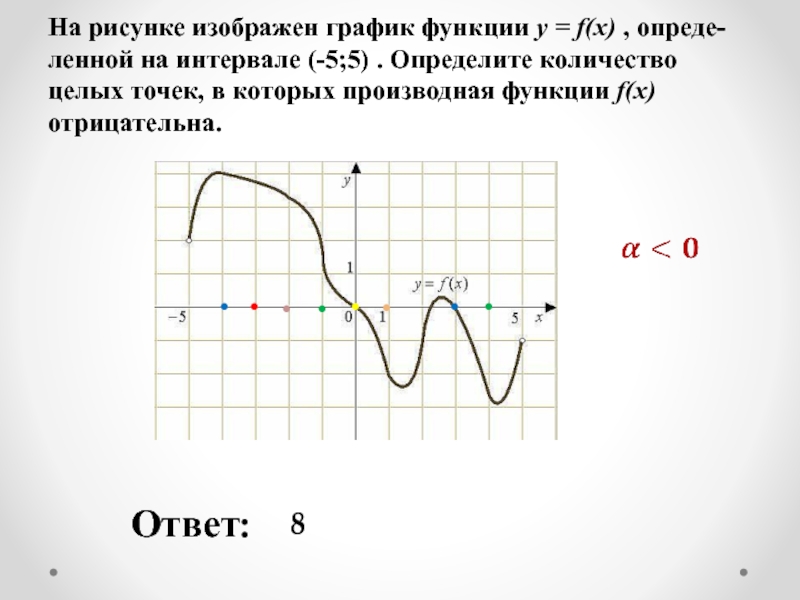
Слайд 3На рисунке изображен график функции y = f(x) , опреде-ленной на
интервале (-5;5) . Определите количество целых точек, в которых производная функции f(x) отрицательна.
Ответ:
•
•
•
•
•
•
•
•
8
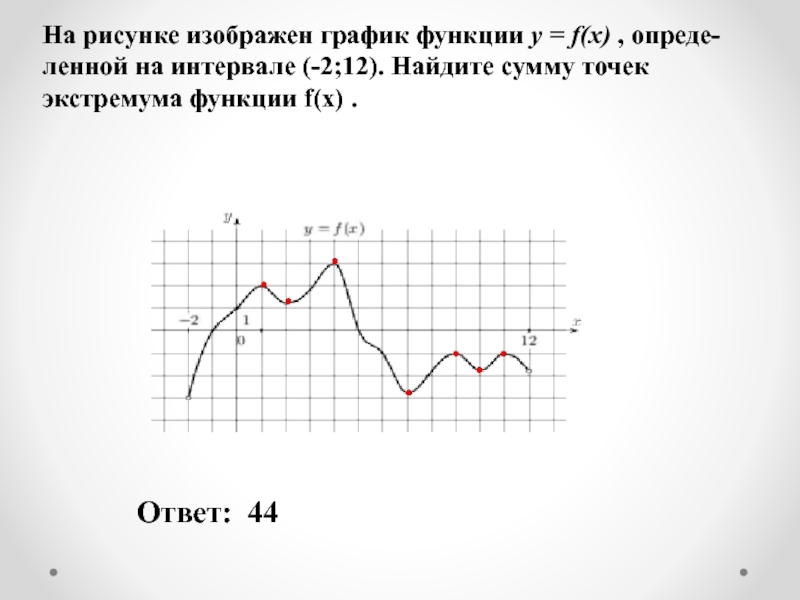
Слайд 4 На рисунке изображен график функции y = f(x) , опреде-ленной на
интервале (-2;12). Найдите сумму точек экстремума функции f(x) .
Ответ: 44
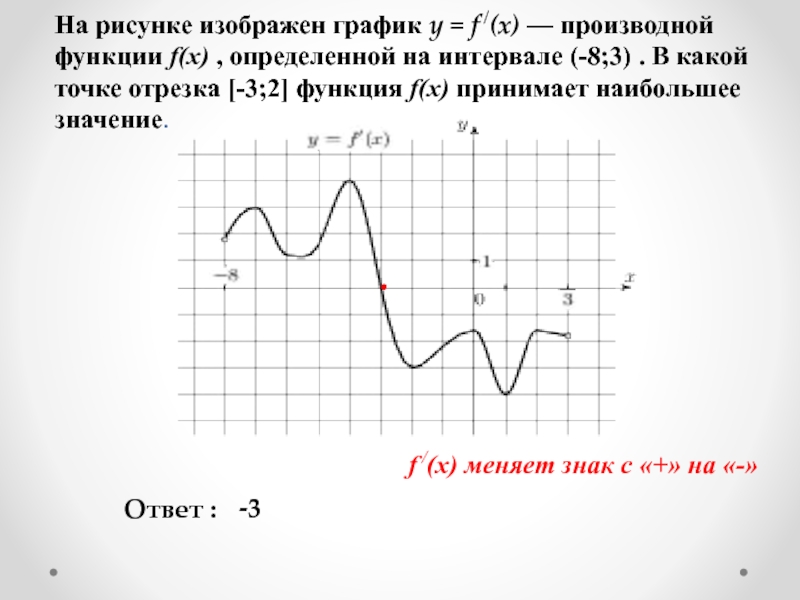
Слайд 5На рисунке изображен график y = f /(x) — производной функции
f(x) , определенной на интервале (-8;3) . В какой точке отрезка [-3;2] функция f(x) принимает наибольшее значение.
Ответ :
f /(x) меняет знак с «+» на «-»
-3
Слайд 6На рисунке изображен график y = f /(x) — производной функции
f(x) , определенной на интервале (-7;14). Найдите количество точек максимума функции f(x) , принадлежащих отрезку [-6;9] .
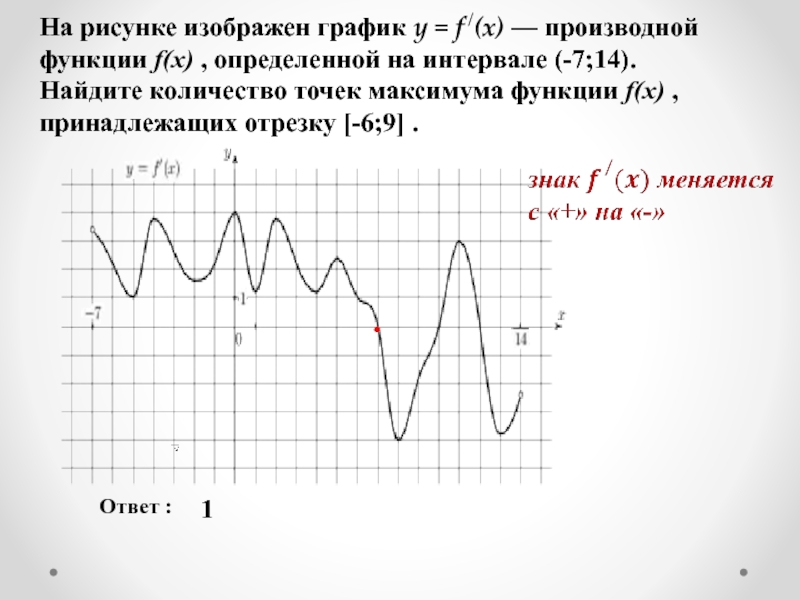
Ответ :
1
Слайд 7На рисунке изображен график y = f /(x) — производной функции
f(x) , определенной на интервале (-11;11). Найдите количество точек экстремума функции f(x) , принадлежащих отрезку [-10;10] .
Ответ:
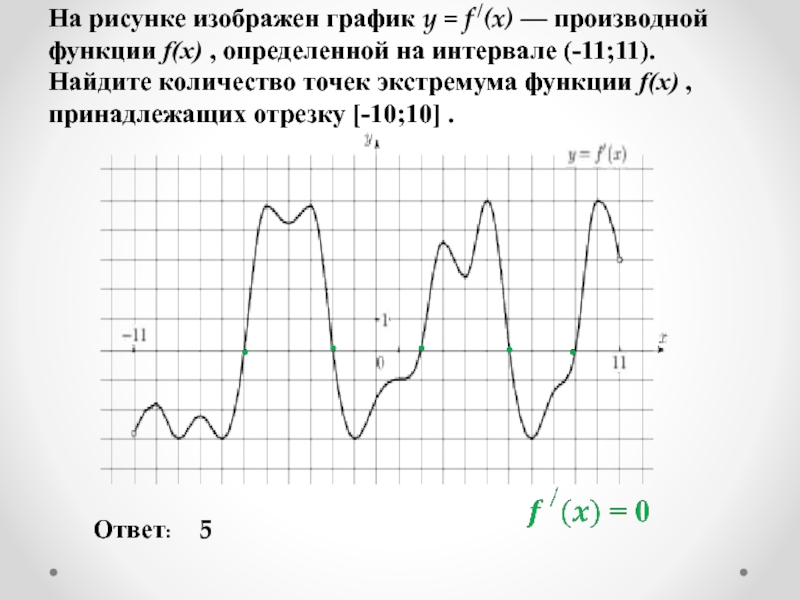
5
Слайд 8На рисунке изображен график y = f /(x) — производной функции
f(x), определенной на интервале (-7;4). Найдите промежутки возрастания функции f(x) . В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ:
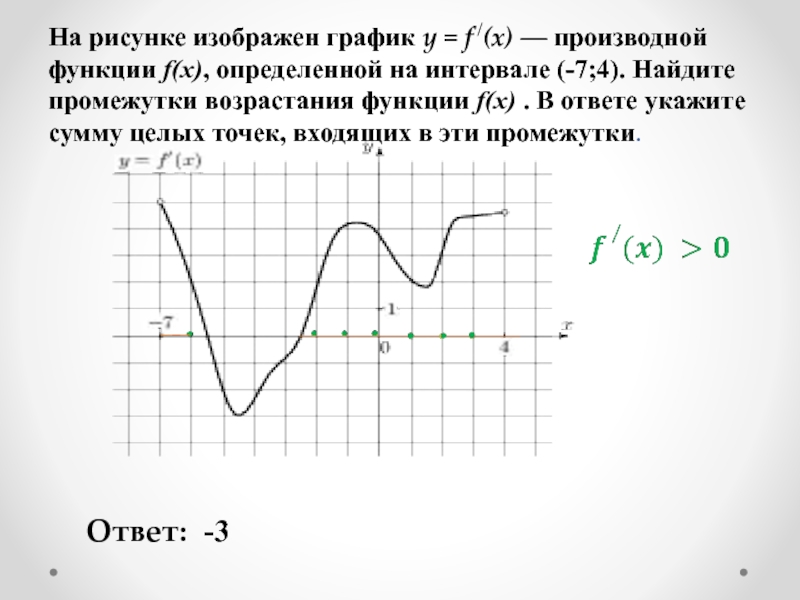
-3
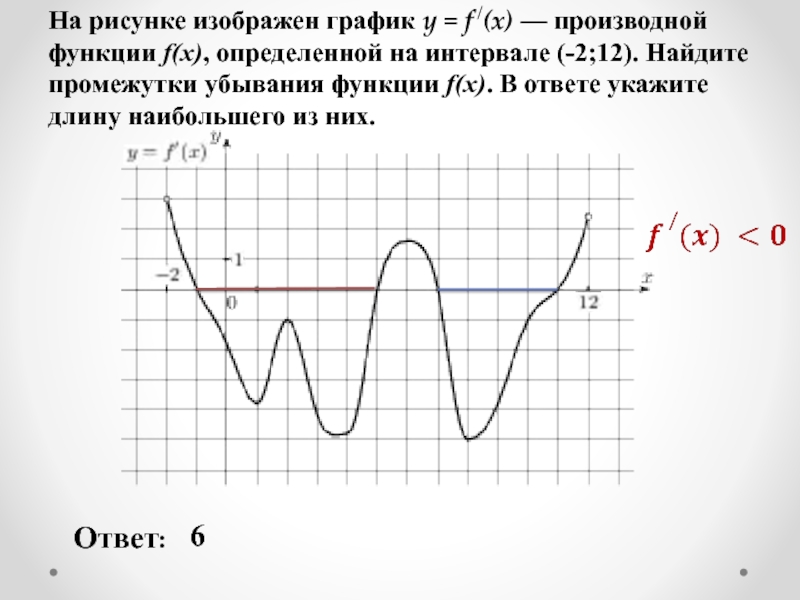
Слайд 9На рисунке изображен график y = f /(x) — производной функции
f(x), определенной на интервале (-11;3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Ответ:
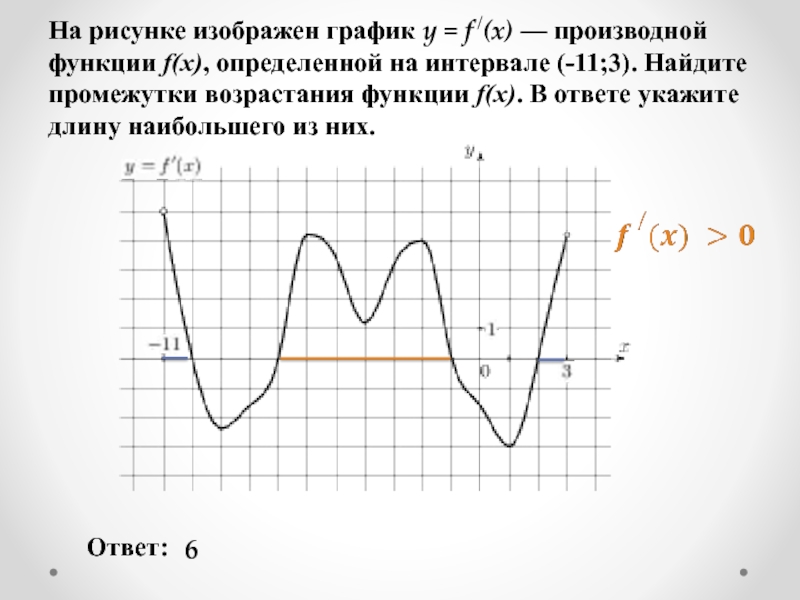
6
Слайд 10На рисунке изображен график y = f /(x) — производной функции
f(x), определенной на интервале (-2;12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Ответ:
6
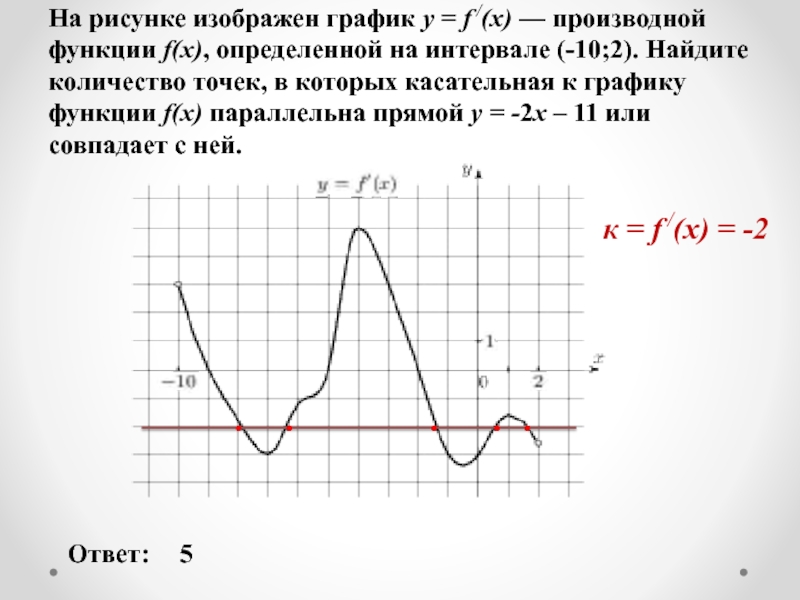
Слайд 11На рисунке изображен график y = f /(x) — производной функции
f(x), определенной на интервале (-10;2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у = -2х – 11 или совпадает с ней.
Ответ:
5
к = f /(x) = -2
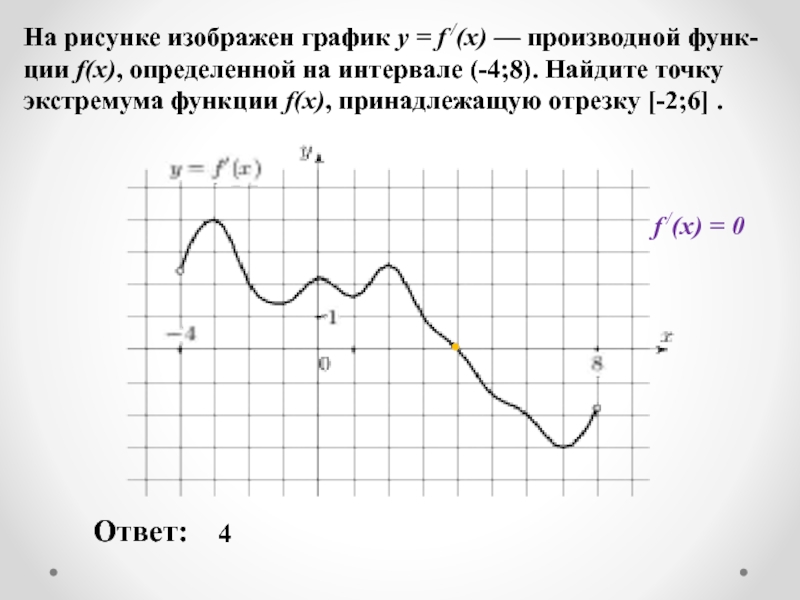
Слайд 12На рисунке изображен график y = f /(x) — производной функ-ции
f(x), определенной на интервале (-4;8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2;6] .
Ответ:
4
f /(x) = 0
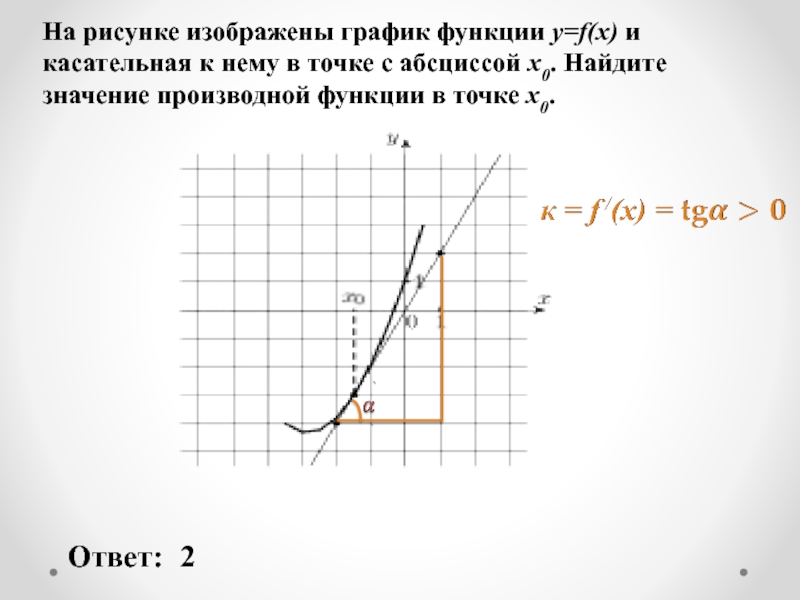
Слайд 13На рисунке изображены график функции y=f(x) и касательная к нему в
точке с абсциссой х0. Найдите значение производной функции в точке х0.
Ответ:
2
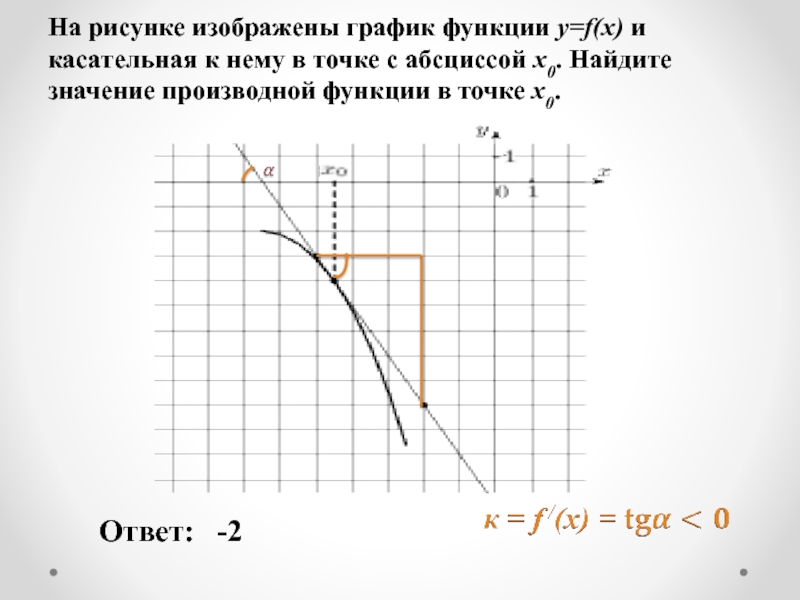
Слайд 14На рисунке изображены график функции y=f(x) и касательная к нему в
точке с абсциссой х0. Найдите значение производной функции в точке х0.
Ответ:
-2
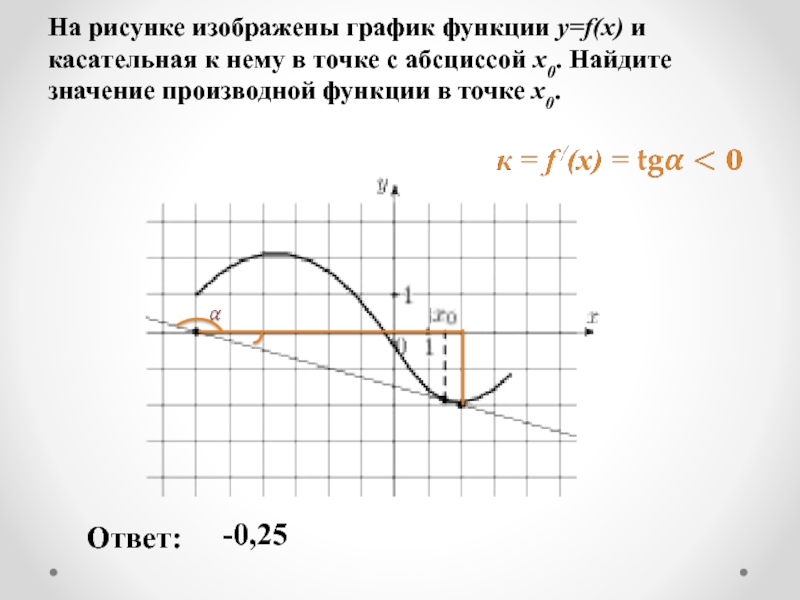
Слайд 15На рисунке изображены график функции y=f(x) и касательная к нему в
точке с абсциссой х0. Найдите значение производной функции в точке х0.
Ответ:
-0,25
Слайд 16На рисунке изображен график y = f /(x) — производной функции
f(x). Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой у = 2х – 2 или совпадает с ней.
Ответ:
5
5
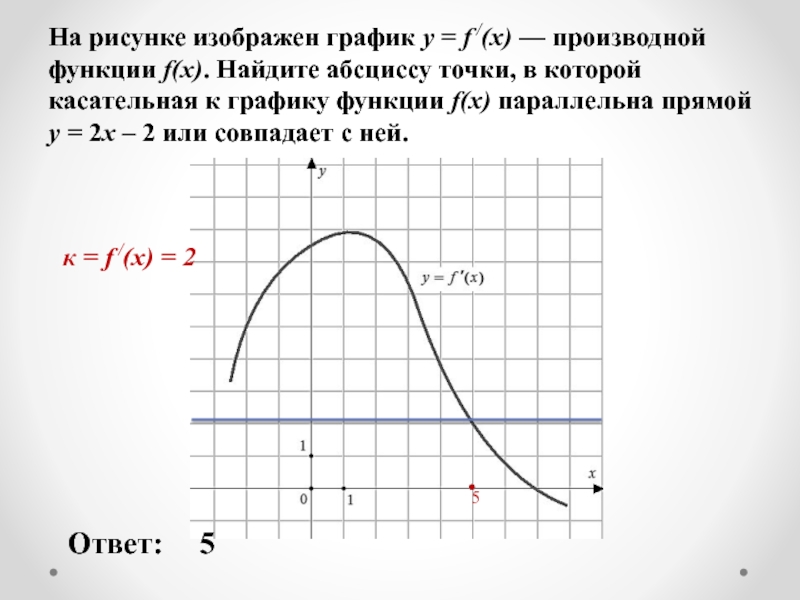
к = f /(x) = 2
Слайд 17На рисунке изображен график y = f /(x) — производной функции
f(x). Найдите абсциссу точки, в которой касательная к графику параллельна оси абсцисс или совпадает с ней.
Ответ:
-3
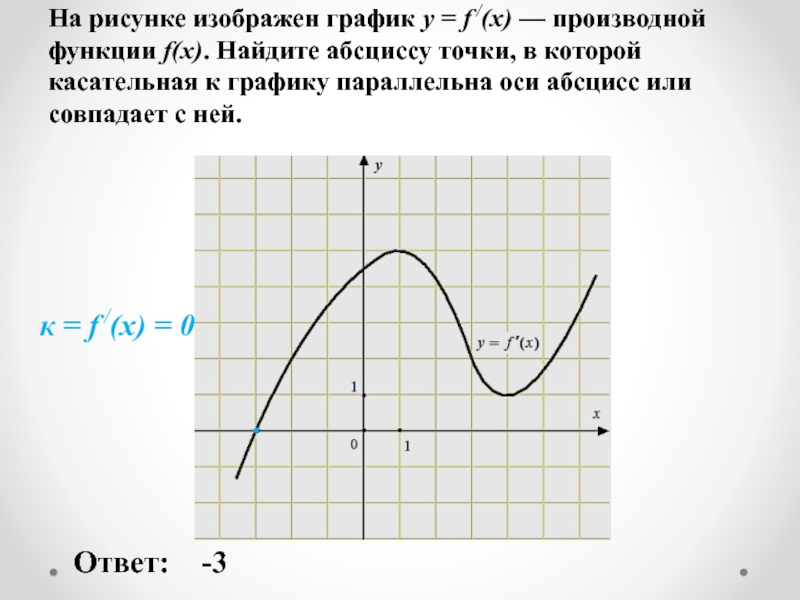
к = f /(x) = 0
Слайд 18 На рисунке изображен график функции y=f(x), определенной на интервале (-5;5).
Найдите количество точек, в которых производная функции равна 0.
Ответ:
4
к = f /(x) = 0
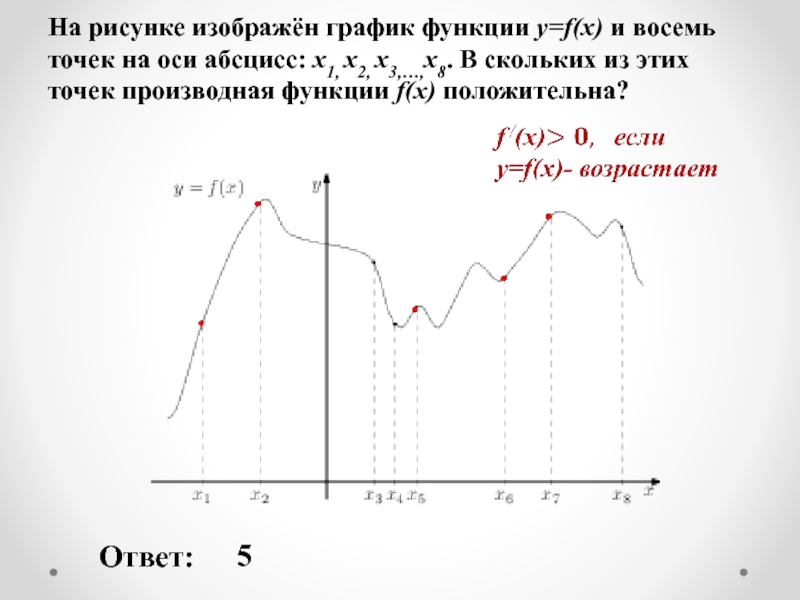
Слайд 19На рисунке изображён график функции y=f(x) и восемь точек на оси
абсцисс: х1, х2, х3,…,х8. В скольких из этих точек производная функции f(x) положительна?
Ответ:
5
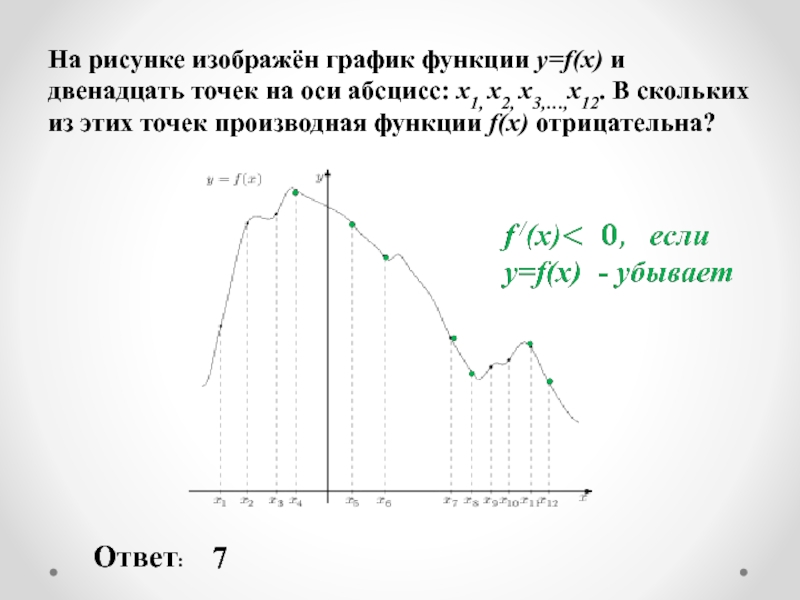
Слайд 20На рисунке изображён график функции y=f(x) и двенадцать точек на оси
абсцисс: х1, х2, х3,…,х12. В скольких из этих точек производная функции f(x) отрицательна?
Ответ:
7
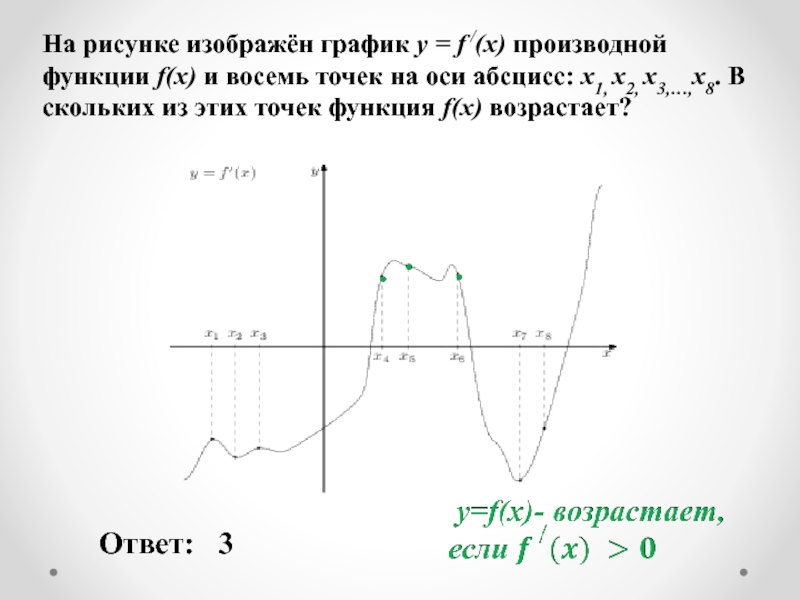
Слайд 21На рисунке изображён график y = f /(x) производной функции f(x)
и восемь точек на оси абсцисс: х1, х2, х3,…,х8. В скольких из этих точек функция f(x) возрастает?
Ответ:
3
