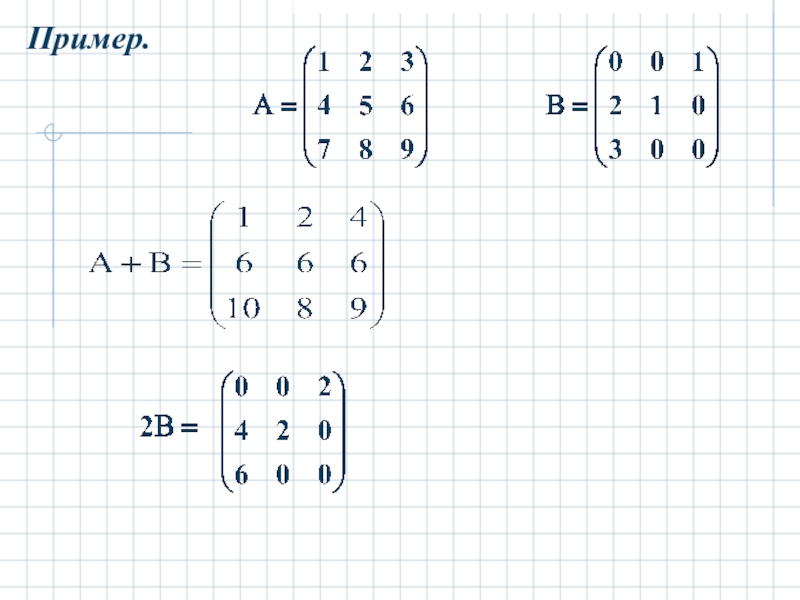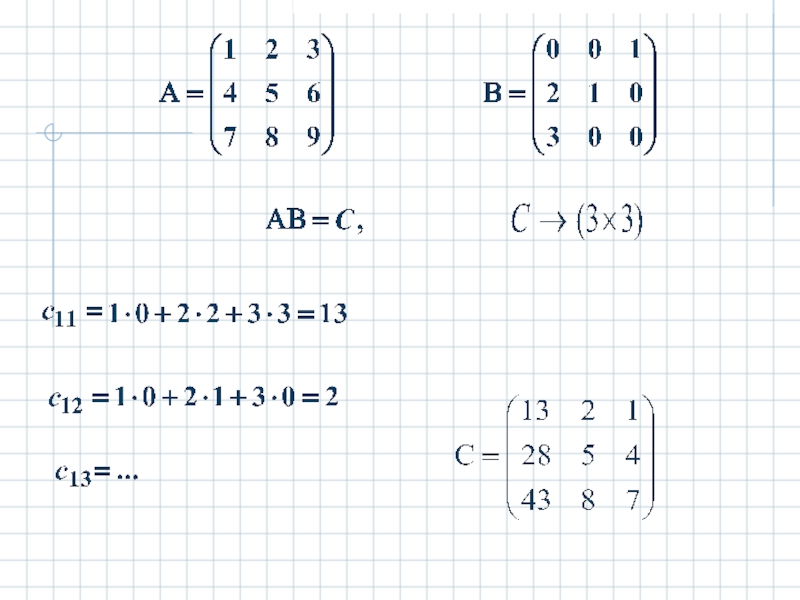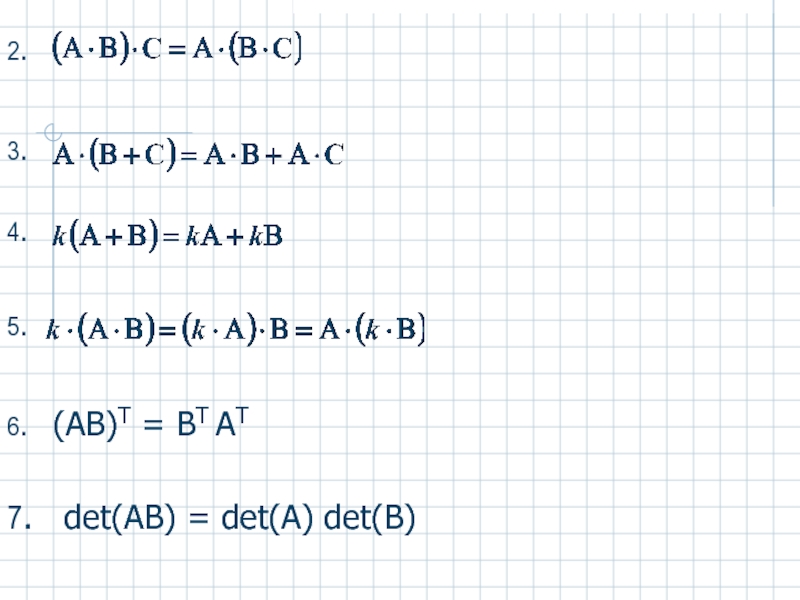- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра матриц презентация
Содержание
- 1. Алгебра матриц
- 2. Лекция 2 Алгебра матриц I.
- 3. Операции над матрицами. Определим
- 4. III. Умножение матрицы на число. IV. Умножение матриц. Здесь:
- 6. Правило умножения матриц :
- 7. Пример.
- 9. Свойства операции сложения:
- 10. 2. 3. 4.
- 11. Обратная матрица. (
- 12. Теорема существования и
- 13. Убедимся, что по указанной формуле находится
- 14. Точно также можно показать, что Таким образом, действительно
- 15. б)Единственность (показать самостоятельно). Пример. Решение. 1.
- 16. Решение матричных уравнений. Пусть А– известная
- 17. Точно также решаются и другие типы
- 18. Обозначим - матрица столбец из неизвестных, –
- 19. Систему (*) тогда можно записать в виде:
- 20. Если А– невырожденная матрица, то существует
- 21. Здесь - определитель системы,
- 22. Вывод: Если определитель системы n
- 23. Ранг матрицы
- 27. Найдите ранг матрицы:
- 28. Найдите ранг матрицы
- 29. МИКРОТЕСТ 2 1. Квадратную матрицу A
- 30. 5. Написать решение уравнения ХA=B. 2)
Слайд 2Лекция 2
Алгебра матриц
I. Операции над матрицами.
2.
3. Решение матричных уравнений.
4. Невырожденные системы n линейных уравнений с n неизвестными.
5. Ранг матрицы и его вычисление методом элементарных преобразований.
Слайд 3 Операции над матрицами.
Определим несколько операций над матрицами.
I. Равенство
II. Сложение матриц .
Результатом сложения матриц А и В называется
матрица С, элементы которой являются суммой
соответствующих элементов исходных матриц :
Слайд 6Правило умножения матриц :
1. Перемножать можно лишь матрицы
размеров (число столбцов матрицы левой равно числу
строк матрицы правой ).
2. Размер матрицы С равен произведению числа строк матрицы А на число столбцов матрицы В, т.е.
(m x n).
Слайд 9Свойства операции сложения:
Рассмотрим матрицы размера (m
1.
2.
Свойства операций умножения на число и умножения матриц:
1.
(В общем случае сомножители менять
местами нельзя).
Слайд 11 Обратная матрица.
(
матрица).
матрица А называется невырожденной.
Слайд 12 Теорема существования и единственности
Для всякой невырожденной матрицы существует
единственная обратная матрица, вычисляемая по
формуле :
Доказательство
а) Существование.
По условию
Слайд 13 Убедимся, что по указанной формуле находится именно
обратная
Вычислим произведение
Слайд 16Решение матричных уравнений.
Пусть А– известная квадратная матрица порядка n ,
В–
X– неизвестная матрица размера (n x m) .
AX=B – матричное уравнение.
Если А– невырожденная матрица,
Слайд 17 Точно также решаются и другие типы уравнений :
уравнений с n неизвестными .
(*)
Слайд 18Обозначим
- матрица столбец из неизвестных,
– матрица из коэффициентов
перед
– матрица столбец из свободных членов.
Слайд 20
Если А– невырожденная матрица, то существует
единственное решение этого матричного уравнения
(1)
(2)
Слайд 21 Здесь
- определитель системы,
-определитель, полученный из определителя
системы заменой i-столбца
свободных членов.
Формулы (2) называются формулами Крамера.
Подробнее:
Слайд 22Вывод:
Если определитель системы n линейных уравнений
с n
Оно может быть найдено одним из трёх способов:
1. матричным способом.
3. методом Гаусса (приведение системы к треугольному виду).
2. по формулам Крамера.
Слайд 23 Ранг матрицы и его вычисление методом
Выделим в матрице размера (m x n) произвольные
k – строк и k - столбцов.
Элементы матрицы, стоящие на их пересечении,
образуют определитель порядка k.
Такой определитель называется минором k- порядка,
этой матрицы.
(Ранг матрицы – это наибольший порядок отличного
от нуля её минора).
Рангом матрицы А называется такое целое число r,
что среди миноров порядка r матрицы А есть хотя бы
один отличный от нуля, а все миноры более высокого
порядка равны нулю.
Слайд 29 МИКРОТЕСТ 2
1. Квадратную матрицу A 4-го порядка (n-го) умножили на
2. Размерность матрицы А - 4х1, B - 1х4. Могут
ли матрицы A и B быть перестановочными?
3. Выделите два требования к матрице А для того чтобы у неё существовала обратная матрица.
4. Дана система из 11 линейных уравнений с 11 неизвестными. Сколько определителей нужно будет вычислить при решении этой системы методом Крамера?
Слайд 305.
Написать решение уравнения ХA=B.
2) Можно ли использовать предложенный способ для решения
3) Какой размерности должна быть матрица A для того, чтобы существовало решение уравнения A*X2x4=B2x4?