- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки параллельных прямых презентация
Содержание
- 1. Признаки параллельных прямых
- 2. Цели: Закрепить знания учащимися видов углов,
- 3. Две прямые параллельны, если они не
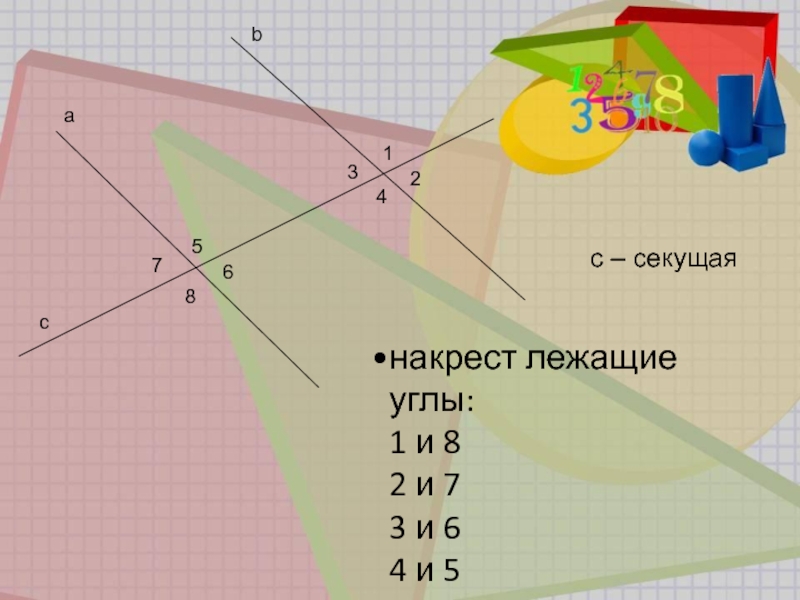
- 4. b a 1 2 3 4 5
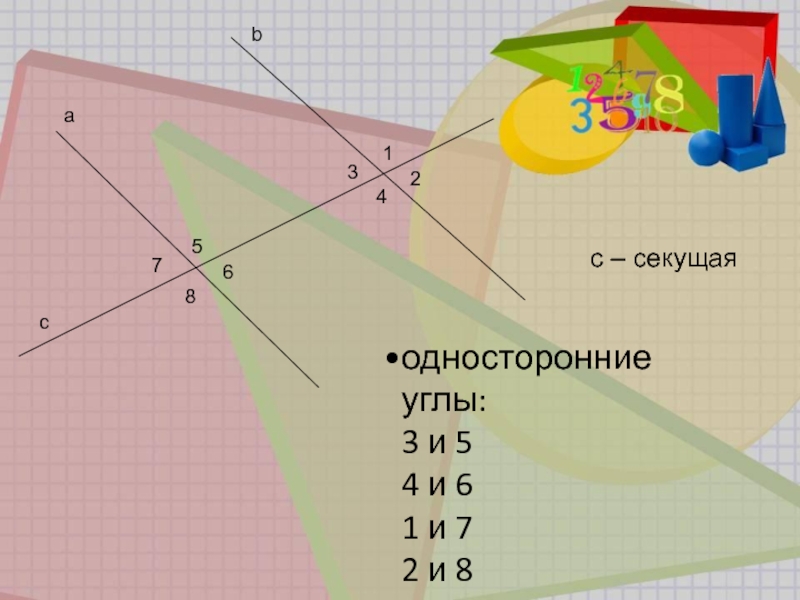
- 5. b a 1 2 3 4 5
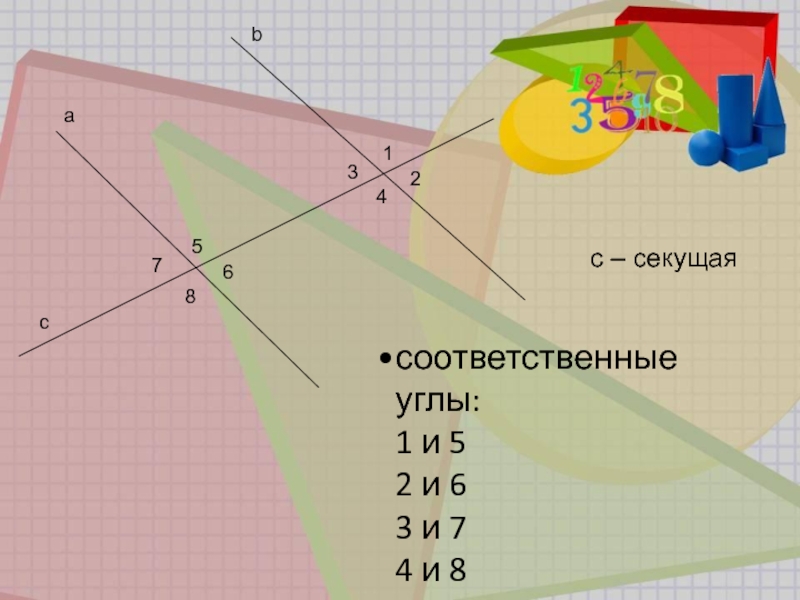
- 6. b a 1 2 3 4 5
- 7. Задание 1.(устно) Назовите пару односторонних углов. Назовите
- 8. Признак 1. Если при
- 9. Доказательство : Случай 1.
- 10. Случай 2. a b c A B
- 11. Признак 2. Если при пересечении двух прямых
- 12. Задание 2.(устно) Докажите, что прямые параллельны. 1 = 2 a b 2 1
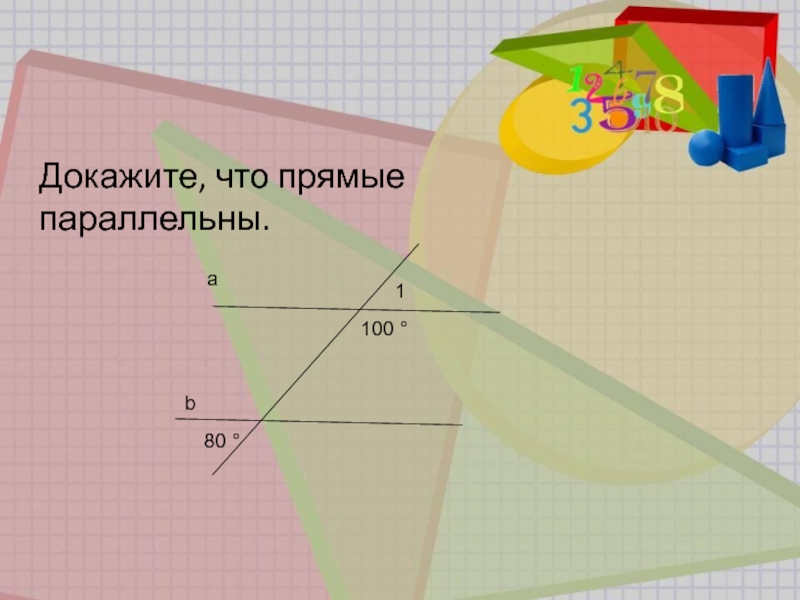
- 13. a b 80 ° 1 100 ° Докажите, что прямые параллельны.
- 14. №187, № 192 Домашнее задание. §1, вопросы 1-6.№188, №193
Слайд 1«Признаки параллельных прямых»
Подготовила учитель математики
МБОУ гимназии №1
Левшина Мария Александровна
Слайд 2Цели:
Закрепить знания учащимися видов углов,
образованных в результате пересечения двух прямых
секущей; изучить признаки параллельности прямых;
формирование умений анализировать изученный материал
и навыков применения его для решения задач; показать
значимость изучаемых понятий; закрепить навыков
решения задач на применение признаков параллельности
прямых;
развитие познавательной активности и самостоятельности
получения знаний;
воспитание интереса к предмету, самостоятельности.
формирование умений анализировать изученный материал
и навыков применения его для решения задач; показать
значимость изучаемых понятий; закрепить навыков
решения задач на применение признаков параллельности
прямых;
развитие познавательной активности и самостоятельности
получения знаний;
воспитание интереса к предмету, самостоятельности.
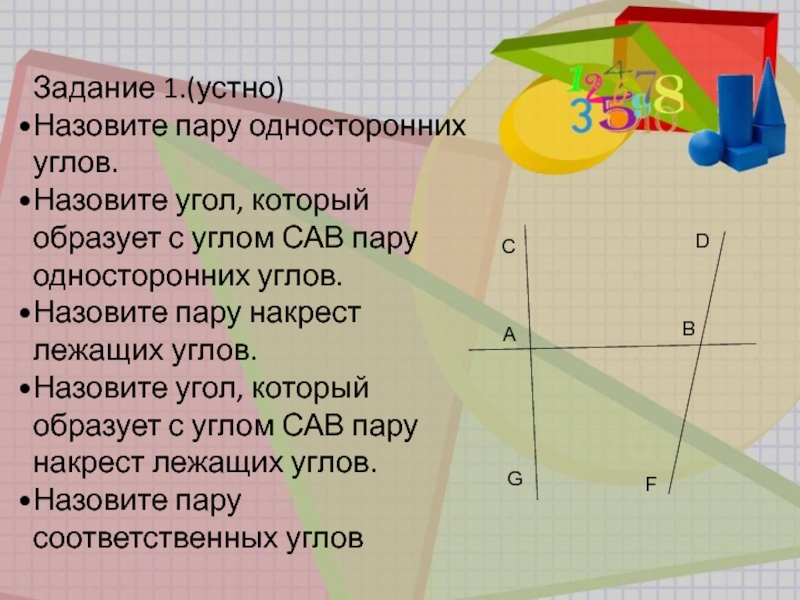
Слайд 7Задание 1.(устно)
Назовите пару односторонних углов.
Назовите угол, который образует с углом САВ
пару односторонних углов.
Назовите пару накрест лежащих углов.
Назовите угол, который образует с углом САВ пару накрест лежащих углов.
Назовите пару соответственных углов
Назовите пару накрест лежащих углов.
Назовите угол, который образует с углом САВ пару накрест лежащих углов.
Назовите пару соответственных углов
C
A
G
D
B
F
Слайд 8
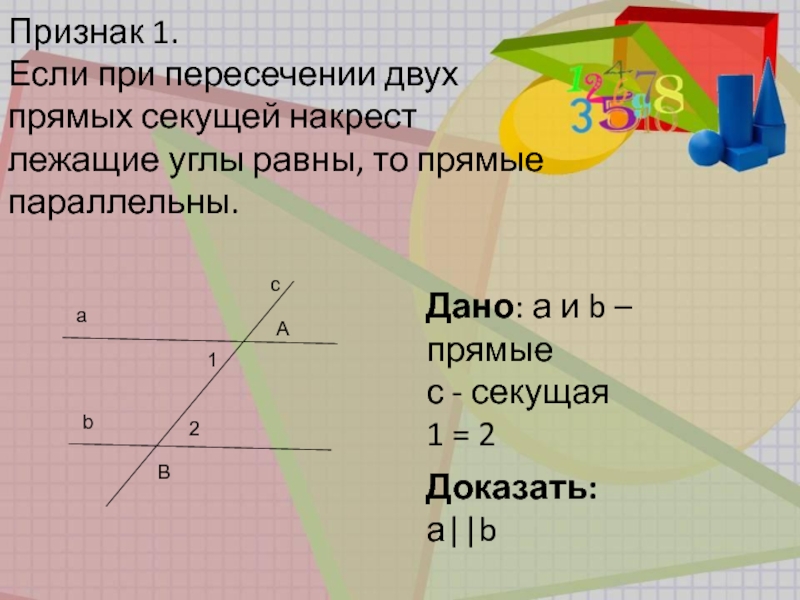
Признак 1.
Если при пересечении двух прямых секущей накрест лежащие углы равны,
то прямые параллельны.
Дано: а и b – прямые с - секущая 1 = 2
Доказать: а||b
a
b
c
A
B
1
2
Слайд 9Доказательство :
Случай 1.
Угол 1 и 2 по 90°.По теореме
о двух прямых, перпендикулярных третьей, а ||‖ b
а
b
c
A
B
1
2
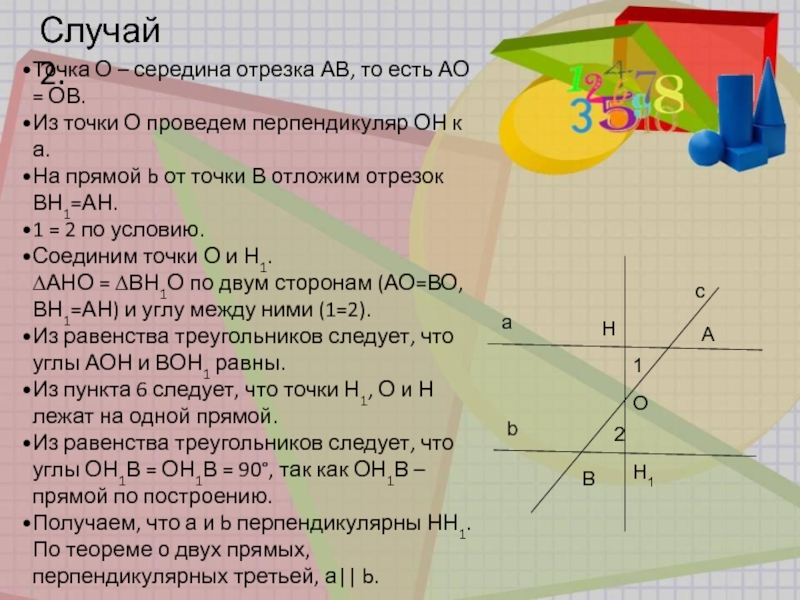
Слайд 10Случай 2.
a
b
c
A
B
1
2
H
H1
O
Точка О – середина отрезка АВ, то есть АО =
ОВ.
Из точки О проведем перпендикуляр ОН к а.
На прямой b от точки В отложим отрезок ВН1=АН.
1 = 2 по условию.
Соединим точки О и Н1.
∆АНО = ∆ВН1О по двум сторонам (АО=ВО, ВН1=АН) и углу между ними (1=2).
Из равенства треугольников следует, что углы АОН и ВОН1 равны.
Из пункта 6 следует, что точки Н1, О и Н лежат на одной прямой.
Из равенства треугольников следует, что углы ОН1В = ОН1В = 90°, так как ОН1В – прямой по построению.
Получаем, что а и b перпендикулярны НН1. По теореме о двух прямых, перпендикулярных третьей, а|| b.
Из точки О проведем перпендикуляр ОН к а.
На прямой b от точки В отложим отрезок ВН1=АН.
1 = 2 по условию.
Соединим точки О и Н1.
∆АНО = ∆ВН1О по двум сторонам (АО=ВО, ВН1=АН) и углу между ними (1=2).
Из равенства треугольников следует, что углы АОН и ВОН1 равны.
Из пункта 6 следует, что точки Н1, О и Н лежат на одной прямой.
Из равенства треугольников следует, что углы ОН1В = ОН1В = 90°, так как ОН1В – прямой по построению.
Получаем, что а и b перпендикулярны НН1. По теореме о двух прямых, перпендикулярных третьей, а|| b.
Слайд 11Признак 2.
Если при пересечении двух прямых секущей сумма односторонних углов равна
180°, то прямые параллельны.
Признак 3.
Если при пересечении прямых секущей соответственные углы равны, то прямые параллельны.
(доказательства самостоятельно дома)
Признак 3.
Если при пересечении прямых секущей соответственные углы равны, то прямые параллельны.
(доказательства самостоятельно дома)