- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 3.2. Криволинейные интегралы. Независимость криволинейного интеграла от пути интегрирования презентация
Содержание
- 1. Лекция 3.2. Криволинейные интегралы. Независимость криволинейного интеграла от пути интегрирования
- 2.
- 3.
- 4.
- 5. Для поверхностей можно ввести понятие стороны поверхности.
- 6. Поверхность называется двухсторонней, если выполнено следующее свойство:
- 7. В дальнейшем будут рассматриваться только двухсторонние поверхности.
- 8. Понятие площади поверхности. Пусть Ф —ограниченная полная
- 9.
- 10.
- 11.
Слайд 5Для поверхностей можно ввести понятие стороны поверхности. Такие поверхности характеризуются, как
двухсторонние поверхности. Их можно выкрасить в два цвета так, что один цвет не будет переходить в другой. Сторону поверхности можно
определить, как множество всех единичных нормалей к поверхности таких, что любые две нормали данной стороны получаются одна из другой непрерывным движением по поверхности вдоль некоторой непрерывной кривой, лежащей на этой поверхности.
Существуют поверхности, не обладающие подобным свойством. Такие поверхности называются односторонними. Примерами односторонних поверхностей могут служить лист Мёбиуса и «бутылка» Клейна.
определить, как множество всех единичных нормалей к поверхности таких, что любые две нормали данной стороны получаются одна из другой непрерывным движением по поверхности вдоль некоторой непрерывной кривой, лежащей на этой поверхности.
Существуют поверхности, не обладающие подобным свойством. Такие поверхности называются односторонними. Примерами односторонних поверхностей могут служить лист Мёбиуса и «бутылка» Клейна.
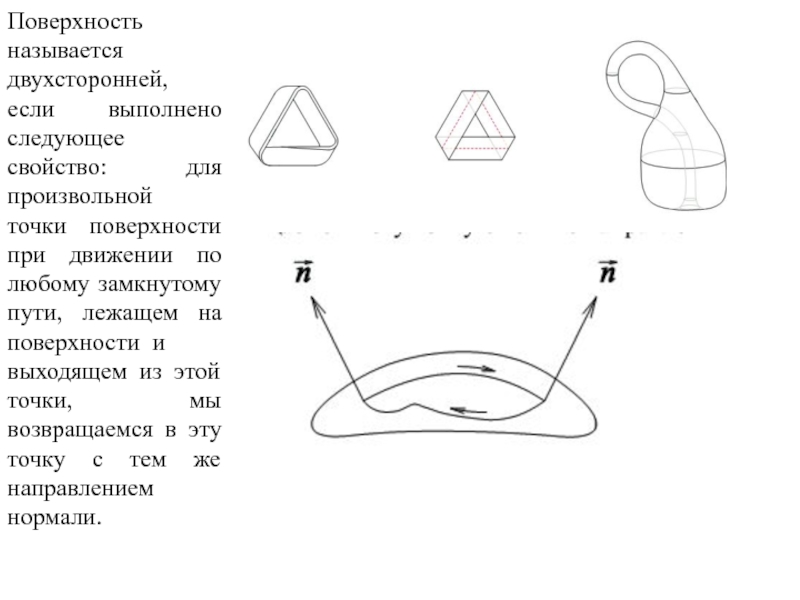
Слайд 6Поверхность называется двухсторонней, если выполнено следующее свойство: для произвольной
точки поверхности
при движении по любому замкнутому пути, лежащем на поверхности и
выходящем из этой точки, мы возвращаемся в эту точку с тем же направлением нормали.
выходящем из этой точки, мы возвращаемся в эту точку с тем же направлением нормали.
Слайд 7В дальнейшем будут рассматриваться только двухсторонние поверхности.
Определение. Поверхность с выбранной
стороной (совокупностью нормалей) называется
ориентированной поверхностью. В любой обыкновенной точке гладкой поверхности существует касательная плоскость.
Нормалью к поверхности Ф в точке M0 называется прямая, проходящая через M0 и перпендикулярная к касательной плоскости в M0. Вектором нормали к поверхности в точке M0 будем называть любой ненулевой вектор, коллинеарный нормали в M0.
Пусть M0 — обыкновенная точка гладкой поверхности Ф. Тогда, вектор N = [ru, rv]
ориентированной поверхностью. В любой обыкновенной точке гладкой поверхности существует касательная плоскость.
Нормалью к поверхности Ф в точке M0 называется прямая, проходящая через M0 и перпендикулярная к касательной плоскости в M0. Вектором нормали к поверхности в точке M0 будем называть любой ненулевой вектор, коллинеарный нормали в M0.
Пусть M0 — обыкновенная точка гладкой поверхности Ф. Тогда, вектор N = [ru, rv]
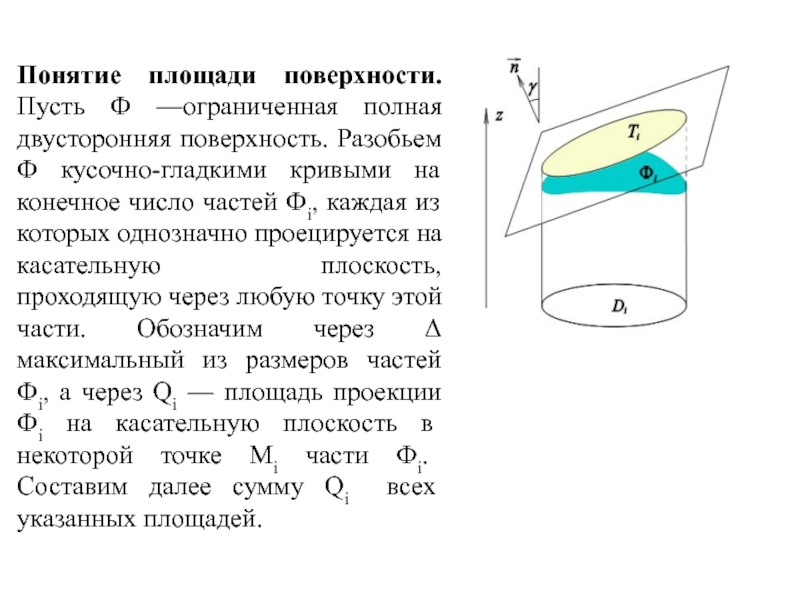
Слайд 8Понятие площади поверхности. Пусть Ф —ограниченная полная двусторонняя поверхность. Разобьем Ф
кусочно-гладкими кривыми на конечное число частей Фi, каждая из которых однозначно проецируется на касательную плоскость, проходящую через любую точку этой части. Обозначим через Δ максимальный из размеров частей Фi, а через Qi — площадь проекции Фi на касательную плоскость в некоторой точке Mi части Фi. Составим далее сумму Qi всех указанных площадей.