- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра. Лекция 4. Количество и сумма натуральных делителей числа. Критерий простоты. Решето Эратосфена презентация
Содержание
- 1. Алгебра. Лекция 4. Количество и сумма натуральных делителей числа. Критерий простоты. Решето Эратосфена
- 2. Количество натуральных делителей числа Теорема
- 3. Сумма натуральных делителей числа Теорема Если
- 4. Примеры
- 5. Теорема (Евклида) Множество простых чисел
- 6. Доказательство теоремы Евклида Предположим, что Р –
- 7. Теорема (критерий простоты) Если число n>1
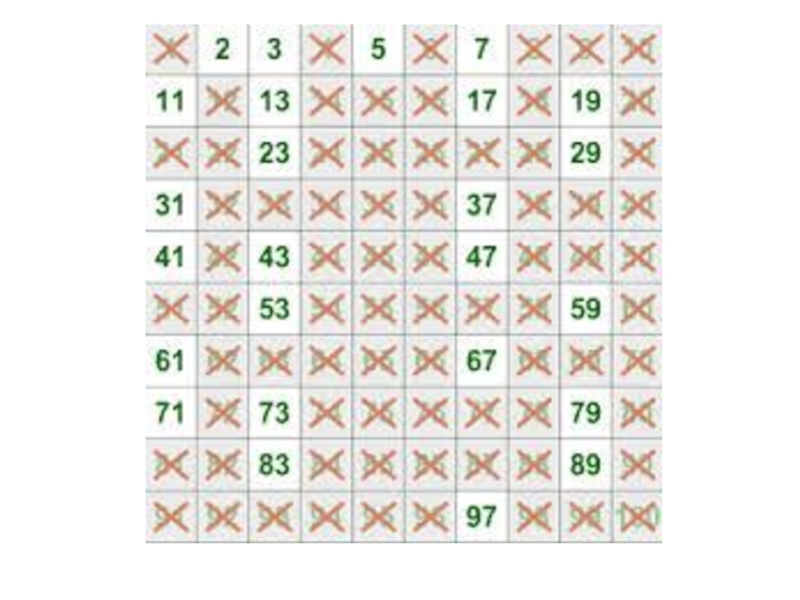
- 8. Решето Эратосфена Эратосфе́н Кире́нский (276 - 194
Слайд 1Лекция 4
Количество и сумма натуральных делителей числа.
Критерий простоты.
Решето Эратосфена
Слайд 2Количество натуральных делителей числа
Теорема
Пусть
Количество натуральных делителей числа n равно τ(n) = (α1 +1)(α2 +1)…(αs +1)
Пример
τ(60)= τ(2²∙3∙5)=(2+1)(1+1)(1+1)=12
Слайд 3Сумма натуральных делителей числа
Теорема
Если
Слайд 6Доказательство теоремы Евклида
Предположим, что Р – последнее, самое большое простое число
Если число М составное, то оно должно иметь по крайней мере один простой делитель
Но этим делителем не может быть ни одно из простых чисел 2, 3, 5, …, Р, поскольку при делении М на каждое из них получается остаток 1
Следовательно, число М либо само простое, либо делится на простое число, большее Р
Значит, предположение, что существует наибольшее простое число Р, неверно и множество простых чисел бесконечно
Слайд 7Теорема (критерий простоты) Если число n>1 и не имеет простых делителей
Доказательство
Если бы п было составным, то n=ab, где 1
Следовательно, хотя бы одно из чисел а и b не превышает
Если, например, число то его простой делитель
Таким образом, любое составное число имеет простой делитель, не превышающий