- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксиомы геометрии презентация
Содержание
- 1. Аксиомы геометрии
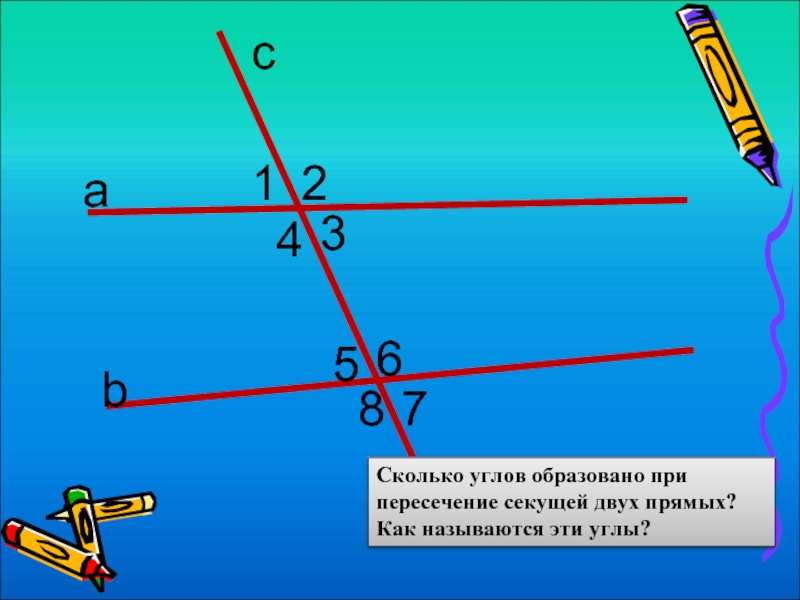
- 2. с а b Сколько углов образовано при
- 3. b bIIc b c Повторите
- 4. Аксиома параллельных прямых
- 5. Теорема Теорема
- 6. Сначала формулируются исходные положения
- 7. Аксиома параллельных прямых М
- 8. Нам представляется, что через т. М нельзя
- 9. Аксиома параллельных прямых А Через точку,
- 10. Если прямая пересекает одну
- 11. Если две прямые параллельны третьей прямой, то
- 12. Решите задачи
- 13. Прямая и обратная теоремы Каждая теорема состоит из УСЛОВИЯ и ЗАКЛЮЧЕНИЯ
- 14. Любую теорему можно записать так, чтобы различить
- 16. Опр. Теорема называется обратной, в случае
- 17. Выполните тест, ответы запишите в тетрадь. Тест
Слайд 2с
а
b
Сколько углов образовано при пересечение секущей двух прямых? Как называются эти
1
2
3
4
5
6
7
8
Слайд 3
b
bIIc
b
c
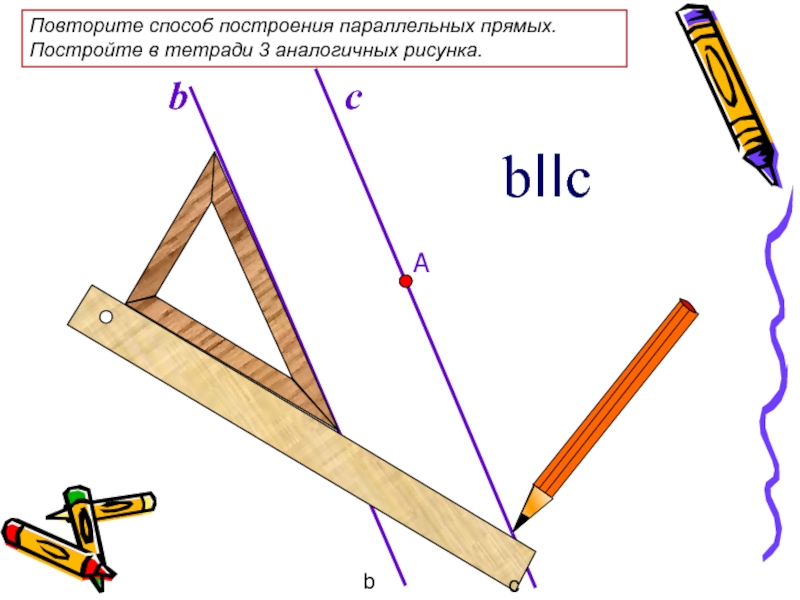
Повторите способ построения параллельных прямых. Постройте в тетради 3 аналогичных рисунка.
Слайд 5Теорема
Теорема
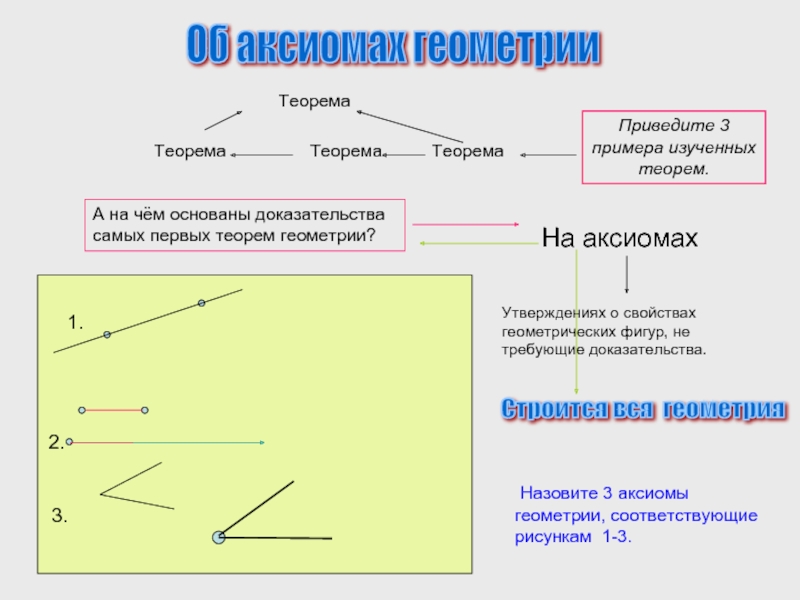
Об аксиомах геометрии
А на чём основаны доказательства самых первых теорем геометрии?
На аксиомах
Утверждениях о свойствах геометрических фигур, не требующие доказательства.
2.
Приведите 3 примера изученных теорем.
Назовите 3 аксиомы геометрии, соответствующие рисункам 1-3.
1.
3.
Строится вся геометрия
Слайд 6
Сначала формулируются исходные положения - аксиомы
На их основе, путём логических рассуждений
Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида
365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».
Слайд 8Нам представляется, что через т. М нельзя провести прямую (отличную от
А можем ли мы это доказать?
Ответ на этот непростой вопрос дал великий русский математик Н.И. Лобачевский. Он выяснил, что это утверждение доказать нельзя, т.к. само является аксиомой.
Слайд 9Аксиома параллельных прямых
А
Через точку, не лежащую на прямой проходит только
Опр.
Следствие – это утверждение, которое выводится непосредственно из аксиом и теорем.
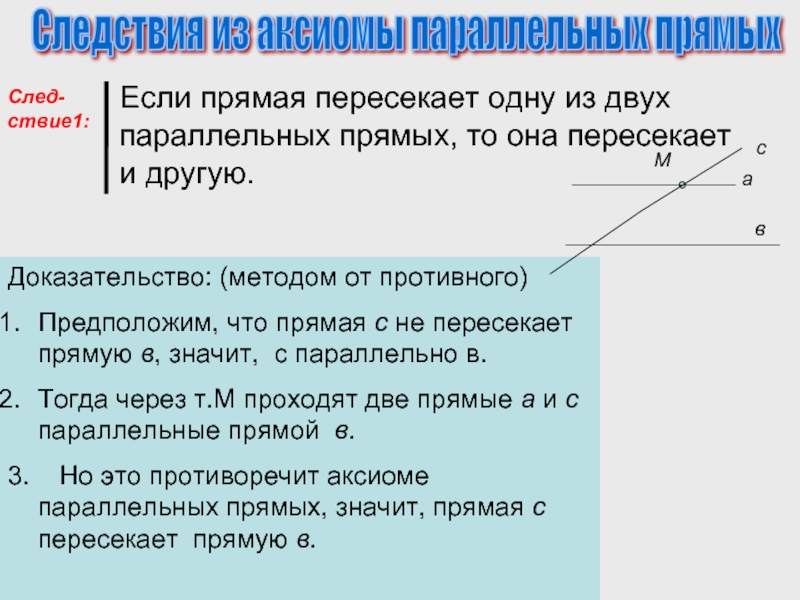
Слайд 10 Если прямая пересекает одну из двух параллельных прямых,
Следствия из аксиомы параллельных прямых
Доказательство: (методом от противного)
Предположим, что прямая с не пересекает прямую в, значит, с параллельно в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
След-ствие1:
Слайд 11Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство: (метод от
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых.
4. Значит прямые а и в параллельны.
След-
ствие 2:
Слайд 12
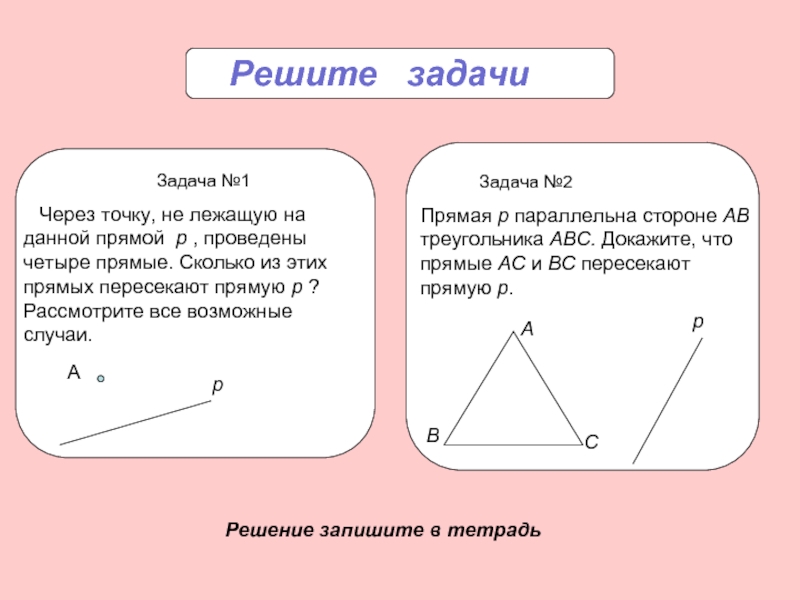
Решите задачи
Задача №1
Через точку, не лежащую на данной прямой p , проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи.
А
р
Задача №2
Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АС и ВС пересекают прямую р.
А
В
С
р
Решение запишите в тетрадь
Слайд 14Любую теорему можно записать так, чтобы различить условие и заключение.
Например:
Если углы вертикальные,
то они равны.
2) Если треугольник равнобедренный, то углы при его основании равны.
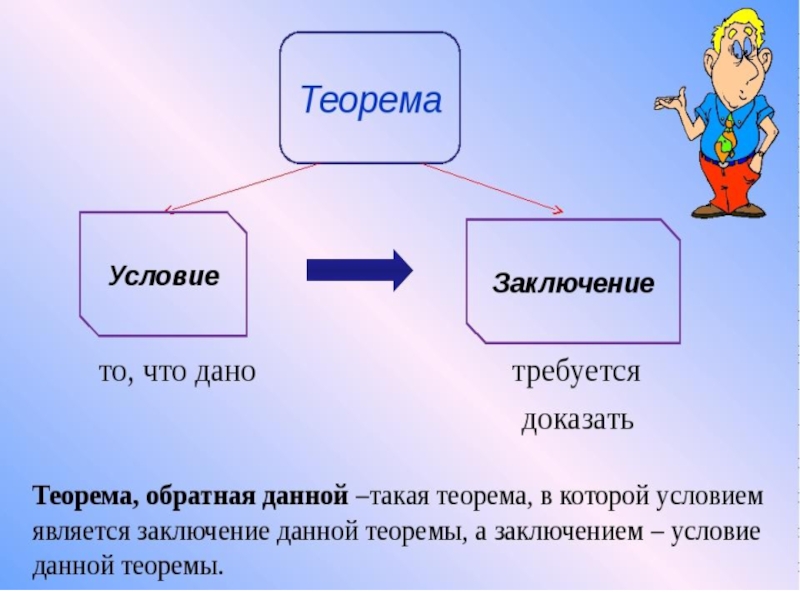
Условие:
Заключение:
Слайд 16Опр.
Теорема называется обратной, в случае когда условие является заключением.
Например:
Обрат-
ная
теорема
Если
Слайд 17Выполните тест, ответы запишите в тетрадь.
Тест по теме «Аксиомы»
1.
2. Аксиома – это утверждение,
а) получаемое путем логического доказательства,
б) истинность которых принимается без доказательства,
в) которое требуется доказать
3. Теорема – это утверждение, …
4.Кто автор работы «Начала»?
5. Из каких частей состоит теорема?
6. Назовите условие и заключение в 1 признаке параллельности прямых.