3
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
3D графіка в науках про землю. (Лекція 3) презентация
Содержание
- 1. 3D графіка в науках про землю. (Лекція 3)
- 2. Що нового Багато різних систем координат в
- 3. Задачі Повторити основну математику цих перетворень Представляти
- 4. Основні ідеї Об'єкт в модельних координатах Перетворення
- 5. Терміни 2D перетворення: обертання, масштабування, зсув Композитне перетворення 3D обертання Переміщення: однорідні координати Трансформація нормалей
- 6. Масштаб(нерівномірний) transformation_game.jar
- 7. Зсув
- 8. Поворот 2D простий, 3D складний. [Похідні? Приклади?]
- 9. Поворот transformation_game.jar
- 10. Поворот
- 11. Композитні трансформації Часто є задачі поєднання трансформацій
- 12. Приклад композитного повороту та масштабування transformation_game.jar
- 13. Обернені композитні трансформації Припустимо, ми хочемо зробити
- 14. Поворот
- 15. Поворот
- 16. Поворот в 3D
- 17. Геометрична інтерпретація 3D поворотів
- 18. Геометрична інтерпретація 3D поворотів
- 19. Геометрична інтерпретація 3D поворотів
- 20. Не комутативні Не коммутативні (на відміну від
- 21. Довільна формула обертання
- 22. Формула повороту навколо осі (Axis–angle representation) Крок
- 23. Формула повороту навколо осі (Axis–angle representation) Крок
- 24. Формула повороту навколо осі (Axis–angle representation)
- 25. Формула повороту навколо осі (Axis–angle representation)
- 26. Формула повороту навколо осі (Axis–angle representation) https://www.youtube.com/watch?v=sgoeQFOxwYA
- 27. Формула повороту навколо осі (Axis–angle representation)
Що нового Багато різних систем координат в графіці Глобальні, моделі, тіла, руки, ... Щоб зв'язати їх, ми повинні зробити трансформації між ними Крім того, для моделювання об'єктів. У нас є чайник,
Слайд 2Що нового
Багато різних систем координат в графіці
Глобальні, моделі, тіла, руки, ...
Щоб
зв'язати їх, ми повинні зробити трансформації між ними
Крім того, для моделювання об'єктів. У нас є чайник, але
Необхідно помістити його на потрібне місце в глобальних координатах
Необхідно переглянути його з різних кутів (ЛБ2)
Необхідно його масштабувати, щоб зробити більшим або меншим
Демо ЛБ2
Крім того, для моделювання об'єктів. У нас є чайник, але
Необхідно помістити його на потрібне місце в глобальних координатах
Необхідно переглянути його з різних кутів (ЛБ2)
Необхідно його масштабувати, щоб зробити більшим або меншим
Демо ЛБ2
Слайд 3Задачі
Повторити основну математику цих перетворень
Представляти перетворення, використовуючи матричне і матрично-векторне множення.
Зробити
Демо лекції: ЛБ2 і аплету
Трансформації аплету
Програмне забезпечення Brown University Exploratories
http://www.cs.brown.edu/exploratories/home.html
Розроблено: Andries Van Dam і Jean Laleuf
Трансформації аплету
Програмне забезпечення Brown University Exploratories
http://www.cs.brown.edu/exploratories/home.html
Розроблено: Andries Van Dam і Jean Laleuf
Слайд 4Основні ідеї
Об'єкт в модельних координатах
Перетворення координат у глобальні
Представлення точки на об'єкті
як вектори
Матричне множення
Демо аплету
Матричне множення
Демо аплету
Слайд 5Терміни
2D перетворення: обертання, масштабування, зсув
Композитне перетворення
3D обертання
Переміщення: однорідні координати
Трансформація нормалей
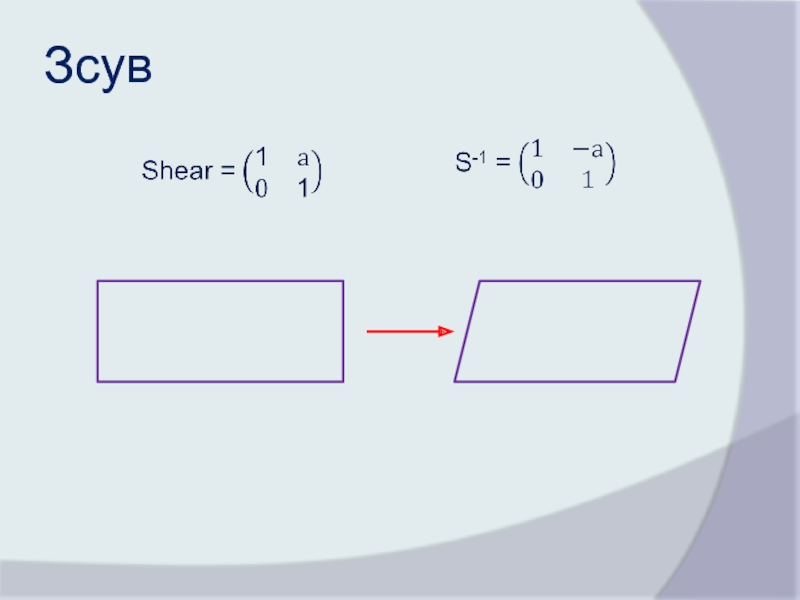
Слайд 8Поворот
2D простий, 3D складний. [Похідні? Приклади?]
2D?
Тригонометрия
R(X+Y)=R(X)+R(Y)
Лінійний
Комутативний – не важен порядок
для 2 Д(поворот 2д.раб стоЛ)
transformation_game.jar
Слайд 11Композитні трансформації
Часто є задачі поєднання трансформацій
Наприклад спочатку змінити масштаб на 2,
а потім повернути на 45 градусів
Перевага матричного запису: все є матрицями
Не комутативні!! Порядок має значення
Перевага матричного запису: все є матрицями
Не комутативні!! Порядок має значення
Слайд 13Обернені композитні трансформації
Припустимо, ми хочемо зробити обернені перетворення з 3 трансформацій
Варіант
1: Знайти композитну матрицю, інвертувати
Варіант 2: Інвертувати кожну трансформацію і змінити порядок
Очевидно з властивостей матриць, демо
при інвертуванні змінюється порядок
Варіант 2: Інвертувати кожну трансформацію і змінити порядок
Очевидно з властивостей матриць, демо
при інвертуванні змінюється порядок
Слайд 20Не комутативні
Не коммутативні (на відміну від 2D) !!
Поворот х навколо у
не такий же, як у навколо х
Порядок застосування поворотів має значення
Слідує з властивостей матриць - множення НЕ комутативне
R1 * R2 не те ж що R2 * R1
Демо: ЛБ2, порядок вправо або вгору матиме значення
Порядок застосування поворотів має значення
Слідує з властивостей матриць - множення НЕ комутативне
R1 * R2 не те ж що R2 * R1
Демо: ЛБ2, порядок вправо або вгору матиме значення
Слайд 22Формула повороту навколо осі (Axis–angle representation)
Крок 1: b має компоненту паралельну
і перпендикулярну a
Паралельна компонента не змінюється (обертання навколо осі площини таке, що вісь обертання залишається незмінною після обертання, наприклад, поворот навколо z)
Паралельна компонента не змінюється (обертання навколо осі площини таке, що вісь обертання залишається незмінною після обертання, наприклад, поворот навколо z)
Слайд 23Формула повороту навколо осі (Axis–angle representation)
Крок 2: Визначимо с ортогональний a
і b
Аналогічно визначимо Y вісь
Використовуємо векторний добуток і матричну формулу для цього
Аналогічно визначимо Y вісь
Використовуємо векторний добуток і матричну формулу для цього
Слайд 25Формула повороту навколо осі (Axis–angle representation)
Компонента вздовж a (відповідно не змінюється)
сos,
що не змінюється
Перпендикуляр (компонента що повертається)
Слайд 26Формула повороту навколо осі (Axis–angle representation)
https://www.youtube.com/watch?v=sgoeQFOxwYA
