- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Красота мира глазами математики презентация
Содержание
- 1. Красота мира глазами математики
- 2. «Пристальное и
- 3. Оглавление Введение Понятие золотого сечения Немного истории
- 4. Введение
- 5. Известно ли вам:
- 6. Золотое сечение в природе Золотое сечение в
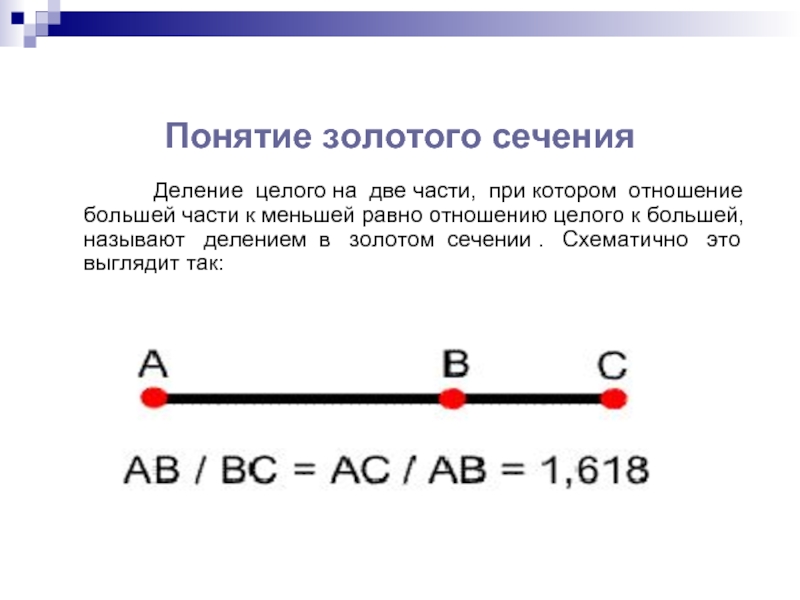
- 7. Понятие золотого сечения
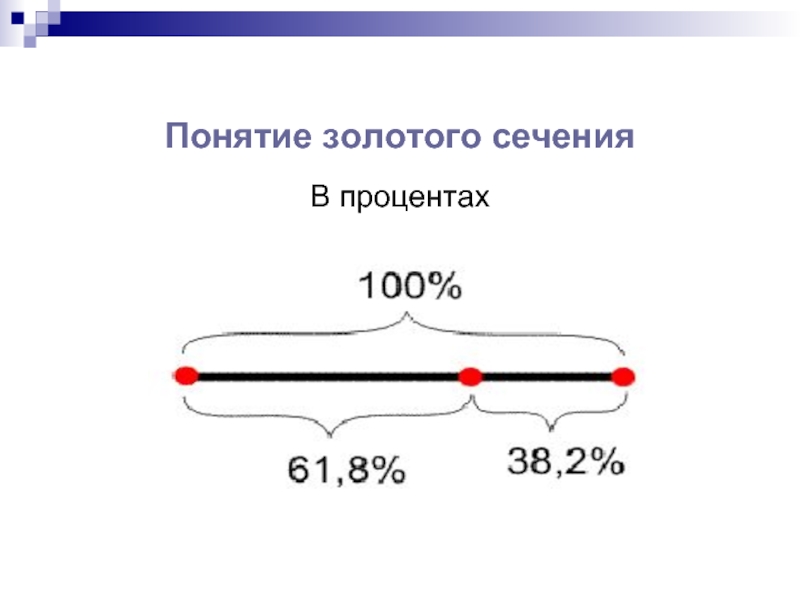
- 8. Понятие золотого сечения В процентах
- 9. Понятие золотого сечения
- 10. Золотое сечение «Геометрия владеет двумя сокровищами:
- 11. Немного истории
- 12. Пифагор Самосский Самосский (VI
- 13. Леонардо да Винчи (1452 - 1519)
- 14. Золотое сечение в строении снежинок
- 15. Золотое сечение в строении вирусов
- 16. Золотое сечение и растения
- 17. Золотое сечение в животном мире
- 18. Золотое сечение в животном мире У многих
- 19. Золотое сечение в животном мире
- 20. Золотое сечение в животном мире Это знакомое
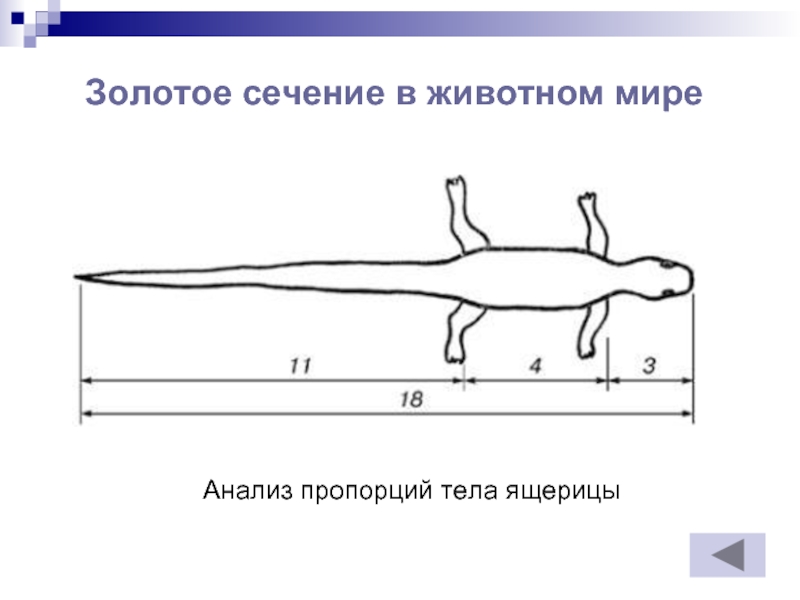
- 21. Золотое сечение в животном мире Анализ пропорций тела ящерицы
- 22. Золотое сечение в пропорциях лица человека
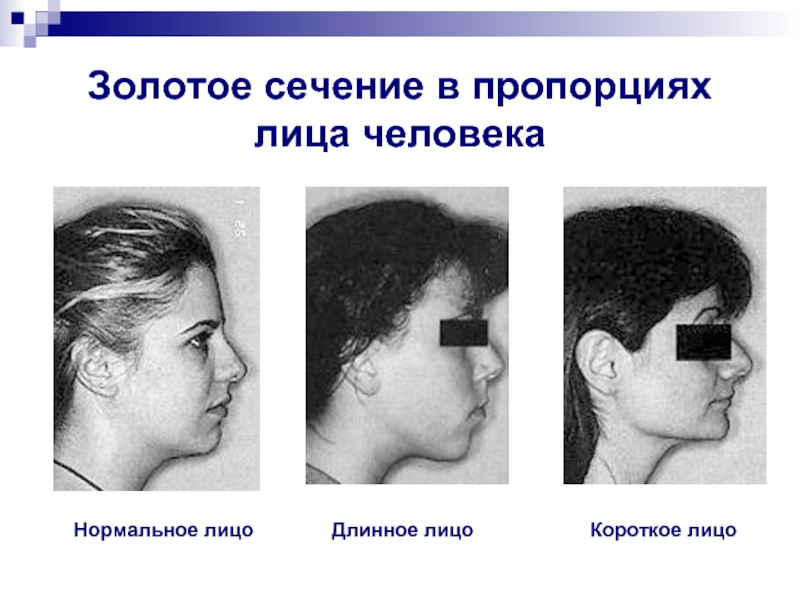
- 23. Золотое сечение в пропорциях лица человека Нормальное лицо Длинное лицо Короткое лицо
- 24. Золотое сечение и пропорции лица человека
- 25. Золотое сечение в пропорциях лица человека Маска
- 26. Пентаграмма Пентаграмма – тайный
- 27. Пентаграмма В
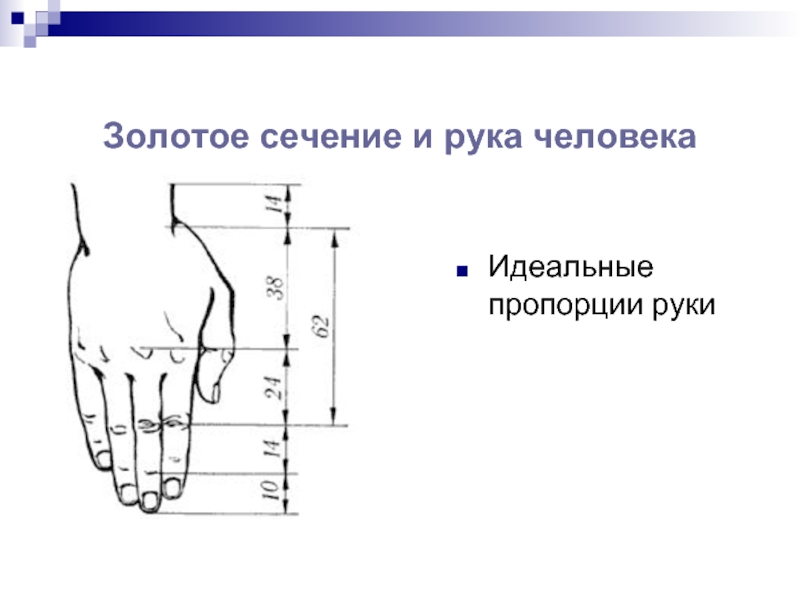
- 28. Золотое сечение и рука человека Идеальные пропорции руки
- 29. Золотое сечение в пропорциях тела Идеальные пропорции тела человека
- 30. Заключение Можно ли измерить
- 31. Источники Золотое сечение в одежде. http://www.olish.ru/stat2.html The
- 32. Золотое сечение в природе Проведите анализ самостоятельно
- 33. Золотое сечение в природе Проведите анализ самостоятельно
- 34. Золотое сечение в пропорциях лица человека Проведите анализ самостоятельно
- 35. Золотое сечение в пропорциях лица человека Проведите анализ самостоятельно
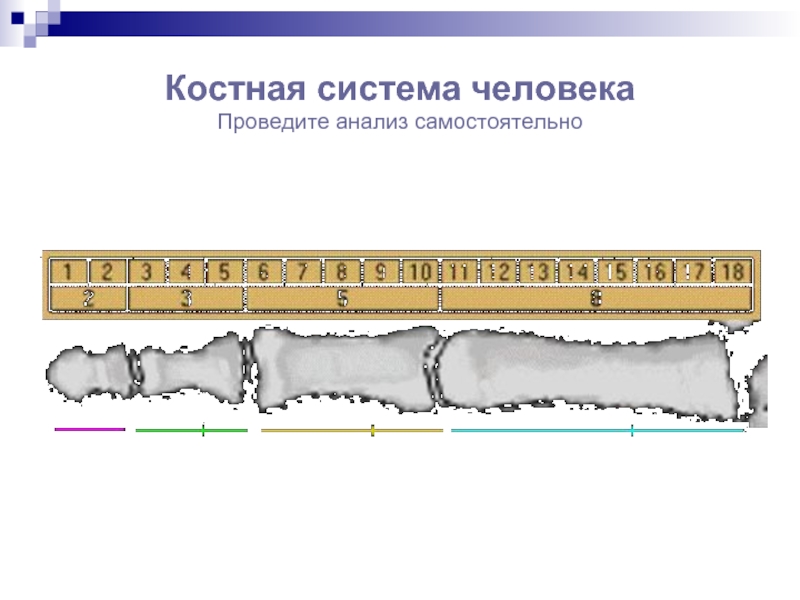
- 36. Костная система человека Проведите анализ самостоятельно
- 37. Золотое сечение в природе Проведите анализ самостоятельно
- 38. Золотое сечение в природе Проведите анализ самостоятельно
- 39. Золотое сечение и мода Проведите анализ самостоятельно
- 40. Золотое сечение в нашей жизни Проведите анализ самостоятельно
Слайд 2 «Пристальное и глубокое изучение природы
Фурье Ж.
« В задачах, которые ставит перед нами жизнь, экзаменатором является сама природа» Сойер У.
Слайд 3Оглавление
Введение
Понятие золотого сечения
Немного истории
Золотое сечение в природе
Заключение
Задания для самостоятельного исследования
Источники
Слайд 4Введение
Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Слайд 5Известно ли вам:
Что если в улье
Каково соотношение диаметра каждого витка спирали к следующему у любой улитки?
Каково отношение диаметров колец Сатурна?
Во всех случаях получается одно и тоже число, приблизительно равное 1,6 или, если быть точнее
1.61803398874989...
Случайно ли это?
Слайд 6Золотое сечение в природе
Золотое сечение в неживой природе
Золотое сечение в микромире
Золотое
Золотое сечение и животные
Золотое сечение в пропорциях человека
Слайд 7Понятие золотого сечения
Слайд 9Понятие золотого сечения
А теперь возьмем 24
Нормальная температура тела человека - 36,60 умножая ее на 0,62 получим оптимальную температуру для окружающего воздуха - 220. Фантастика!
Применение золотого сечения настолько разнообразны (искусство, наука, архитектура), что у нас не хватило бы времени рассмотреть их все. Поэтому мы остановимся на самом красивом и рассмотрим золотое сечение в природе.
Слайд 10Золотое сечение
«Геометрия владеет двумя сокровищами: одно из них – это
а другое – деление отрезка в «золотом сечении». Первое можно сравнить
с мерой золота; второе же больше напоминает драгоценный камень»
Иоганн Кеплер
Слайд 11Немного истории
Однако есть предположение, что Пифагор понятие золотого сечения позаимствовал у египтян и вавилонян.
И, действительно пропорции пирамиды Хеопса, барельефы предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношением золотого сечения при их создании.
Пирамида Хеопса
Сфинкс, охраняющий гробницу Тутанхамона
Слайд 12Пифагор Самосский Самосский (VI в. до н. э.)
Древнегреческий философ,
религиозный и политический деятель,
Основатель пифагореизма, математик.
Слайд 14Золотое сечение в строении снежинок
Золотое сечение
Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору.
Все изысканные красоты фигур, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках построены по совершенной четкой формуле золотого сечения.
Слайд 15Золотое сечение в строении вирусов
Впервые золотое сечение в
Они показали, что для сферической оболочки вируса самой оптимальной формой является симметрия типа формы икосаэдра.
Вирусы сами сооружают себе столь сложную оболочку из эластичных, гибких белковых клеточных единиц."
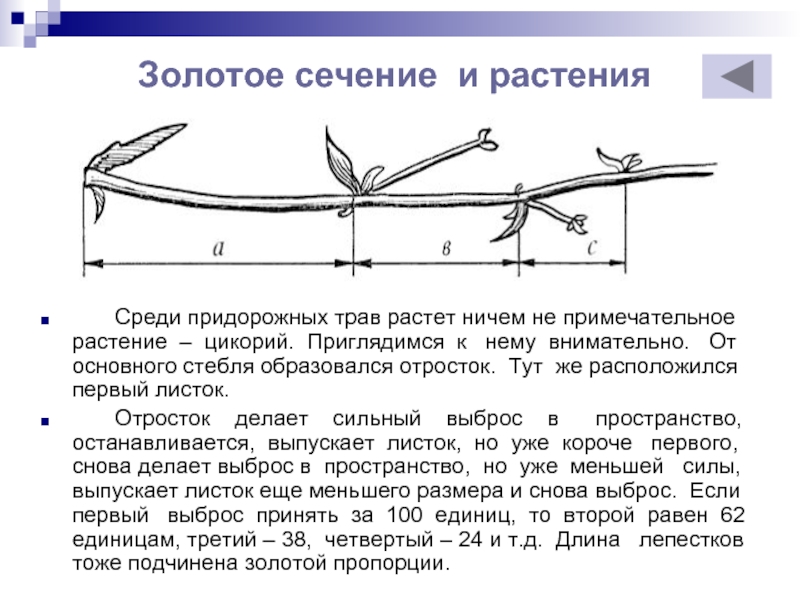
Слайд 16Золотое сечение и растения
Среди придорожных трав растет
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции.
Слайд 17Золотое сечение в животном мире
«Порхающими
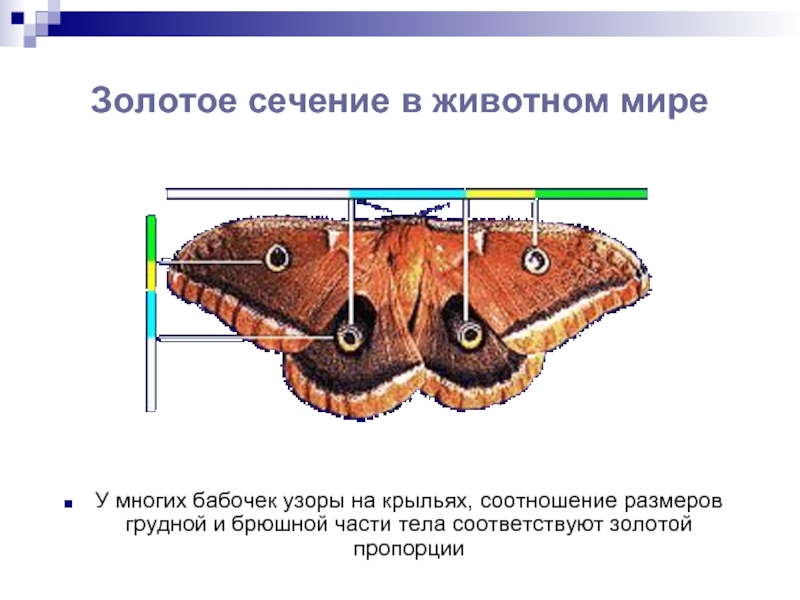
Слайд 18Золотое сечение в животном мире
У многих бабочек узоры на крыльях, соотношение
Слайд 19Золотое сечение в животном мире
Неудивительно, что стрекоза
Слайд 20Золотое сечение в животном мире
Это знакомое существо вы, наверное, не раз
А задумывались ли вы о пропорциях тела ящерицы ?
Слайд 22Золотое сечение в пропорциях лица человека
Чем красивее кажется
Однако, пропорции лица человека меняются в зависимости от мимики.
И даже лицо, пропорции которого в спокойном состоянии далеки от идеальных, в момент радости может быть очень красивым.
Слайд 24Золотое сечение и пропорции лица человека
Американский
в основе которой лежит пентаграмма.
Изобретение было запатентовано и широко используется в пластической хирургии.
Слайд 25Золотое сечение в пропорциях лица человека
Маска идеального лица доктора Stephena Marquardta
Разные
Слайд 26Пентаграмма
Пентаграмма – тайный знак
пифагорейского братства – была выбрана ими в качестве символа жизни и здоровья.
Слайд 27Пентаграмма
В пентаграмме каждая
Пентаграмму изображали для того, чтобы спастись от проникновения в дом злых духов.
Пентаграмма пропорциональна и, значит, красива. Не случайно и сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира.
Слайд 30Заключение
Можно ли измерить красоту нашего мира? На этот
Трудно оторвать глаза от красоты, она так притягательна, может причина в нем – золотом и божественном. Надо заметить, человек способен интуитивно чувствовать пропорции сечения. Работая над картиной, вышивкой или костюмом, сам того не зная, человек закладывает его в свои творения. Ничего удивительного, ведь золотая пропорция у нас всегда перед глазами, в виде самих себя
Слайд 31Источники
Золотое сечение в одежде. http://www.olish.ru/stat2.html
The Divine Proportion. http://goldennumber.net
А.В. Волошинов. Пифагор.-
Г.И. Глейзер. История математики в школе VII-VIII кл. Пособие для учителей.- М: «Просвещение» 1982 г.
Лиман М.М. Школьникам о математике и математиках. М: «Просвещение» 1981 г.