- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория информации. Предмет и задачи информатики. Основные термины и определения. (Лекция 1, 2) презентация
Содержание
- 1. Теория информации. Предмет и задачи информатики. Основные термины и определения. (Лекция 1, 2)
- 2. Введение
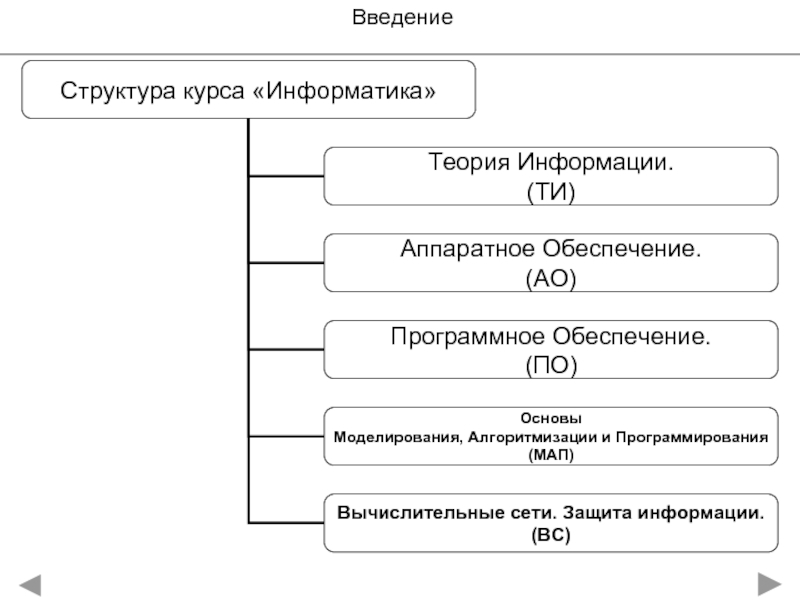
- 3. Введение Распределение лекционного материала (14 ч.)
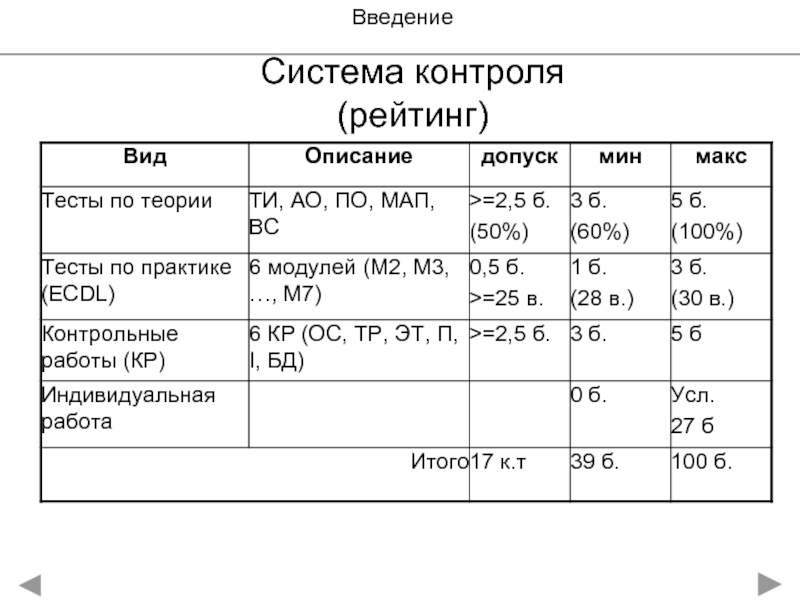
- 4. Введение Система контроля (рейтинг)
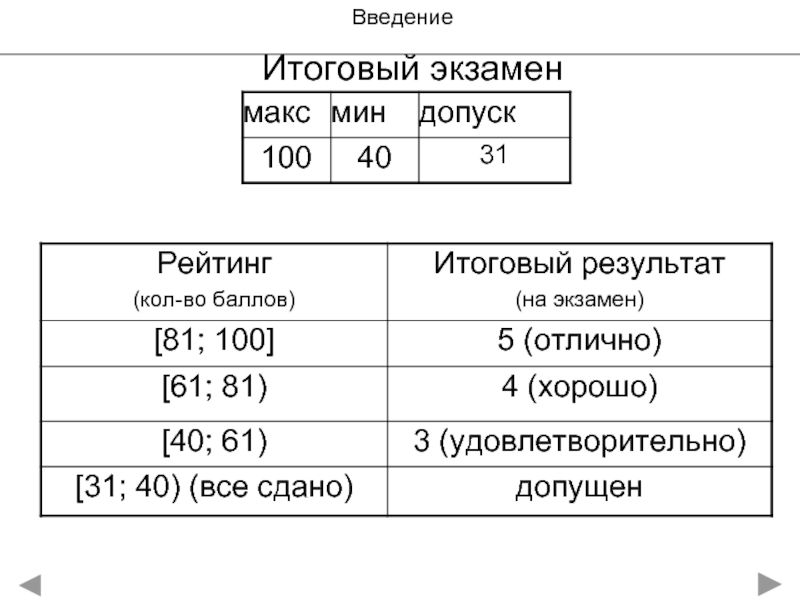
- 5. Введение Итоговый экзамен
- 6. Предмет и задачи информатики. Основные термины и
- 7. Информация – способность материи отражаться в окружающей
- 8. Виды сигналов непрерывный по уровню непрерывный во
- 9. Свойства информации (качество): Любую информацию можно: Создать,
- 10. Информатика – наука, систематизирующая приемы создания, обработки,
- 11. Информационная технология – это совокупность методов, производственных
- 12. Лекция №2 Теория информации. 1. Роль информатики
- 13. Лекция №2 Теория информации. 1. Роль информатики
- 14. Лекция №2 Теория информации. 1. Роль информатики
- 15. Лекция №2 Теория информации. 1. Роль информатики
- 16. Лекция №2 Теория информации. 3. СС, правила
- 17. Лекция №2 Теория информации. 3. СС, правила
- 18. Лекция №2 Теория информации. 3. СС, правила
- 19. Лекция №2 Теория информации. 3. СС, правила
- 20. Лекция №2 Теория информации. 3. СС, правила
Слайд 6Предмет и задачи информатики. Основные термины и определения
Роль информатики в современном
Исторические вехи развития информатики.
Системы счисления (СС), правила перехода из одной СС в другую.
Лекция №1
Теория информации.
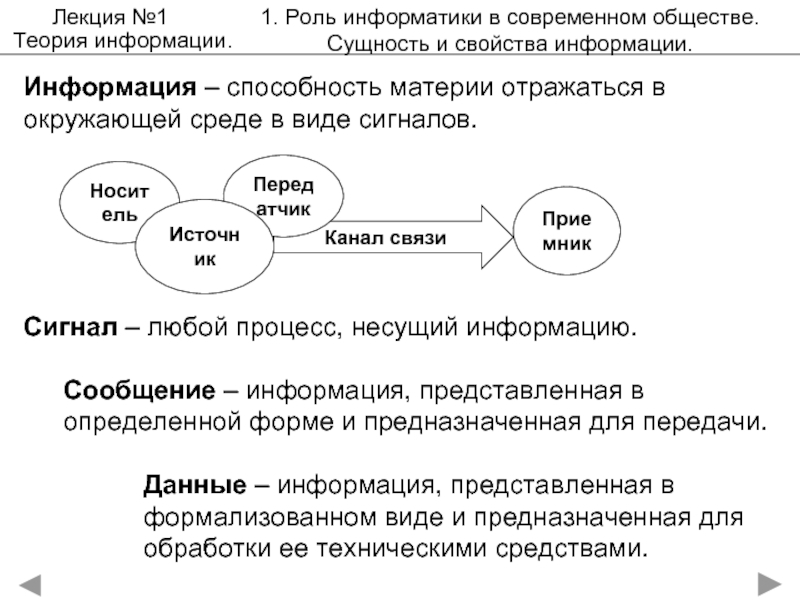
Слайд 7Информация – способность материи отражаться в окружающей среде в виде сигналов.
Сигнал
Сообщение – информация, представленная в определенной форме и предназначенная для передачи.
Данные – информация, представленная в формализованном виде и предназначенная для обработки ее техническими средствами.
Лекция №1
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства информации.
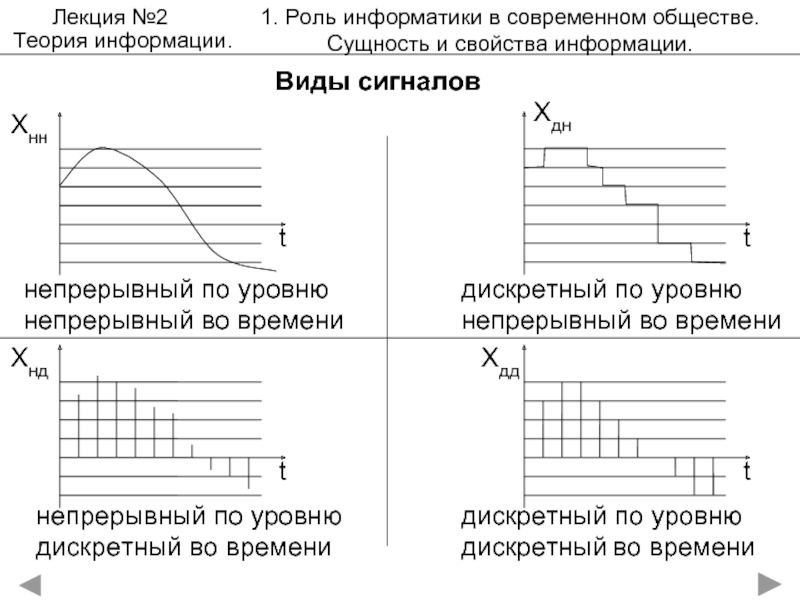
Слайд 8Виды сигналов
непрерывный по уровню
непрерывный во времени
дискретный по уровню
непрерывный во времени
непрерывный по
дискретный во времени
дискретный по уровню
дискретный во времени
Лекция №2
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства информации.
Слайд 9Свойства информации (качество):
Любую информацию можно:
Создать, собрать
Обработать
Передать
Хранить
Лекция №2
Теория информации.
1. Роль информатики в
Объективность
Полнота
Достоверность
Адекватность
Доступность
Актуальность
Эмоциональность
Классификация информации
http://ru.wikipedia.org
Слайд 10Информатика – наука, систематизирующая приемы создания, обработки, передачи и хранения данных
Лекция №2
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства информации.
Слайд 11Информационная технология – это совокупность методов, производственных процессов и программно-технических средств,
Лекция №2
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства информации.
Слайд 12Лекция №2
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства
Информационная система - система, реализующая автоматизированный сбор, обработку и манипулирование данными и включающая технические средства обработки данных, программное обеспечение и обслуживающий персонал.
Слайд 13Лекция №2
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства
Понятие количества информации
Количеством информации называют числовую характеристику сигнала, отражающую ту степень неопределенности (неполноту знаний), которая исчезает после получения сообщения в виде данного сигнала.
Эту меру неопределенности в теории информации называют энтропией.
Бит – количество информации, которое можно получить при ответе на вопрос типа «да-нет».
Бит – минимальная единица количества информации.
Слайд 14Лекция №2
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства
Понятие количества информации
Формула Хартли:
i – количество информации в битах
N – число возможных состояний
Байт – группа из 8 бит. (1 б = 8 бит).
1 б = 8 бит
1 кб = 210 б =1024 б
1 Мб = 210 кб = 220 б = 1048576 б
1 Гб = 210 Мб = 220 кб = 230 б
1 Тб = 210 Гб = 220 Мб = 230 кб = 240 б
Слайд 15Лекция №2
Теория информации.
1. Роль информатики в современном обществе. Сущность и свойства
Понятие количества информации
Примеры решения задач
1) Перевести 6 Мб в бит и ТБ.
2) Экзаменационный билет в ГАИ содержит 20 вопросов. Каждый вопрос снабжен 4 вариантами ответов. Какое количество информации получает экзаменующий после проверки билета?
3) Письмо написано с использованием букв из 32 символьного алфавита. Сколько букв содержалось в письме, если после его прочтения была получена информация в количестве 10 байт?
Слайд 16Лекция №2
Теория информации.
3. СС, правила перехода из одной СС в другую.
СС,
Счисление – совокупность приемов наименования и записи чисел.
Система счисление – способ представления любого числа с помощью алфавита символов, называемых цифрами.
Система счисление
позиционные
непозиционные
алфавит может быть не ограничен
алфавит ограничен
вес цифры зависит от ее положения в алфавите и от занимаемой позиции в числе
вес цифры зависит от ее положения в алфавите и не зависит от занимаемой позиции в числе
XIX, XXI
219, 291
Слайд 17Лекция №2
Теория информации.
3. СС, правила перехода из одной СС в другую.
СС,
Количество символов в алфавите позиционной СС называют её основанием (q).
q=10 (десятичная СС) – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Пример: 243(10), 58,09(10)
q=8 (восьмеричная СС) – 0, 1, 2, 3, 4, 5, 6, 7
Пример: 243(8), 77(8)
q=2 (двоичная СС) – 0, 1
Пример: 10011(2), 110,11(2)
q=16 (шестнадцатеричная СС) – 0, 1, …, 9, А, B, C, D, E, F
Пример: 243(16), A2,F3(10), CAD(10)
Слайд 18Лекция №2
Теория информации.
3. СС, правила перехода из одной СС в другую.
СС,
Арифметические операции в различных СС
Двоичная СС
Слайд 19Лекция №2
Теория информации.
3. СС, правила перехода из одной СС в другую.
СС,
Преобразование чисел
I. Перевод из любой СС в десятичную (X(q)→X(10)):
Необходимо число X(q) разложить в виде суммы произведений, выполнить арифметические действия, полученной число есть X(10).
Пример: 1001(2) → X(10)
1001(2)=1*23+0*22+0*21+1*20=8+1=9(10)
Слайд 20Лекция №2
Теория информации.
3. СС, правила перехода из одной СС в другую.
СС,
Преобразование чисел
II. Перевод из десятичной СС в любую (X(10) →X(q)):
Необходимо число X(10) целочисленно разделить на основание новой СС q. Остаток выделить.
Если полученное частное (ответ) не меньше q, то его повторно делим на q. Остаток выделяем.
Если полученное частное меньше q, записываем результат перевода в виде последовательности остатков, начиная от последнего частного.
Пример: 37(10) → X(2)