- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория алгоритмов. Алгоритмы сортировки массивов. (Лекция 2) презентация
Содержание
- 1. Теория алгоритмов. Алгоритмы сортировки массивов. (Лекция 2)
- 2. Алгоритм сортировки Сортировка - это процесс упорядочения
- 3. Критерии оценки алгоримов Время — основной параметр,
- 4. Классификация алгоритмов сортировки Устойчивость (stability) — устойчивая
- 5. Классификация по области применения Внутренняя сортировка
- 6. Также алгоритмы классифицируются по: потребности в дополнительной
- 7. Алгоритмы устойчивой сортировки Сортировка обменная (пузырьком) (англ. Bubble
- 8. Алгоритмы неустойчивой сортировки Сортировка выбором (Selection sort)
- 9. Прочие алгоритмы сортировки Сортировка перестановкой — O(n·n!)
- 10. Сортировка обменом (пузырьковая сортировка) Идея метода: шаг
- 11. Пример
- 12. Пример
- 13. Сортировка «пузырьком» for (int i
- 14. Оптимизация алгоритма Запоминаем, производился ли на данном
- 15. Сортировка выбором Идея метода состоит в том,
- 16. Пример
- 17. Сортировка вставками Идея алгоритма: Предположим последовательность a[0]...a[i]
- 18. Пример
- 19. Сортировка простыми вставками 1 3 4 8
- 20. Сортировка Шелла Сортировка Шелла (англ. Shell sort) — алгоритм
- 21. Сортировка Шелла 1 2 3 4 5
- 22. Сортировка Шелла int n ; //
- 23. Быстрая сортировка Быстрая сортировка (англ. quicksort) — широко
- 24. Быстрая сортировка 1 3 4 8 10
- 25. Быстрая сортировка
- 26. Дополнения и улучшения алгоритма Первый элемент в
- 27. Алгоритм слияния упорядоченных массивов 1 3 4
- 28. 1 3 4 8 10 14 16
- 29. Сортировка подсчетом Этот алгоритм подходит для сортировки
- 31. Цифровая сортировка Цифровая сортировка — один из
- 32. Цифровая сортировка 1 3 4 8 10
- 33. Алгоритмы поиска Одно из наиболее часто встречающихся
- 34. Линейный поиск Данный алгоритм является простейшим алгоритмом
- 35. Двоичный поиск Двоичный поиск (также известен, как
- 36. Двоичный поиск в упорядоченном массиве 1 2
- 38. Алгоритмы STL STL - алгоритмы представляют набор
- 39. Функции для сортировки членов коллекции sort, stable_sort,
Слайд 2Алгоритм сортировки
Сортировка - это процесс упорядочения некоторого множества элементов, на котором
определены отношения порядка >, <, і , Ј .
Задачей сортировки является преобразование исходной последовательности в последовательность, содержащую те же элементы, но в порядке возрастания (или убывания) значений.
Задачей сортировки является преобразование исходной последовательности в последовательность, содержащую те же элементы, но в порядке возрастания (или убывания) значений.
Слайд 3Критерии оценки алгоримов
Время — основной параметр, характеризующий быстродействие алгоритма. Для типичного
алгоритма хорошее поведение — это O(n log n) и плохое поведение — это O(n²). Идеальное поведение для упорядочения — O(n). Алгоритмы сортировки, использующие только абстрактную операцию сравнения ключей всегда нуждаются по меньшей мере в O(n log n) сравнениях в среднем;
Память — ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.
Память — ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.
Слайд 4Классификация алгоритмов сортировки
Устойчивость (stability) — устойчивая сортировка не меняет взаимного расположения
равных элементов.
Естественность поведения — эффективность метода при обработке уже упорядоченных, или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
Использование операции сравнения. Алгоритмы, использующие для сортировки сравнение элементов между собой, называются основанными на сравнениях. Минимальная трудоемкость худшего случая для этих алгоритмов составляет O(n log n) , но они отличаются гибкостью применения. Для специальных случаев (типов данных) существуют более эффективные алгоритмы.
Естественность поведения — эффективность метода при обработке уже упорядоченных, или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
Использование операции сравнения. Алгоритмы, использующие для сортировки сравнение элементов между собой, называются основанными на сравнениях. Минимальная трудоемкость худшего случая для этих алгоритмов составляет O(n log n) , но они отличаются гибкостью применения. Для специальных случаев (типов данных) существуют более эффективные алгоритмы.
Слайд 5Классификация по области применения
Внутренняя сортировка оперирует с массивами, целиком помещающимися
в оперативной памяти с произвольным доступом к любой ячейке. Данные обычно упорядочиваются на том же месте, без дополнительных затрат.
Внешняя сортировка оперирует с запоминающими устройствами большого объёма, но с доступом не произвольным, а последовательным (упорядочение файлов). Это накладывает некоторые дополнительные ограничения на алгоритм и приводит к специальным методам упорядочения, обычно использующим дополнительное дисковое пространство. Кроме того, доступ к данным на носителе производится намного медленнее, чем операции с оперативной памятью.
Внешняя сортировка оперирует с запоминающими устройствами большого объёма, но с доступом не произвольным, а последовательным (упорядочение файлов). Это накладывает некоторые дополнительные ограничения на алгоритм и приводит к специальным методам упорядочения, обычно использующим дополнительное дисковое пространство. Кроме того, доступ к данным на носителе производится намного медленнее, чем операции с оперативной памятью.
Слайд 6Также алгоритмы классифицируются по:
потребности в дополнительной памяти или её отсутствии;
потребности
в знаниях о структуре данных, выходящих за рамки операции сравнения, или отсутствии таковой .
Слайд 7Алгоритмы устойчивой сортировки
Сортировка обменная (пузырьком) (англ. Bubble sort ) — сложность алгоритма:
O(n2); для каждой пары индексов производится обмен, если элементы расположены не по порядку.
Сортировка перемешиванием (Шейкерная, Cocktail sort, bidirectional bubble sort) — Сложность алгоритма: O(n2)
Гномья сортировка — имеет общее с сортировкой пузырьком и сортировкой вставками. Сложность алгоритма — O(n2).
Сортировка вставками (Insertion sort) — Сложность алгоритма: O(n2); определяем где текущий элемент должен находиться в упорядоченном списке и вставляем его туда
Блочная сортировка (Корзинная сортировка, Bucket sort) — Сложность алгоритма: O(n); требуется O(k) дополнительной памяти и знание о природе сортируемых данных, выходящее за рамки функций "переставить" и "сравнить".
Сортировка подсчётом (Counting sort) — Сложность алгоритма: O(n+k); требуется O(n+k) дополнительной памяти (рассмотрено 3 варианта)
Сортировка слиянием (Merge sort) — Сложность алгоритма: O(n log n); требуется O(n) дополнительной памяти; выстраиваем первую и вторую половину списка отдельно, а затем — сливаем упорядоченные списки
Сортировка с помощью двоичного дерева (англ. Tree sort) — Сложность алгоритма: O(n log n); требуется O(n) дополнительной памяти
Сортировка перемешиванием (Шейкерная, Cocktail sort, bidirectional bubble sort) — Сложность алгоритма: O(n2)
Гномья сортировка — имеет общее с сортировкой пузырьком и сортировкой вставками. Сложность алгоритма — O(n2).
Сортировка вставками (Insertion sort) — Сложность алгоритма: O(n2); определяем где текущий элемент должен находиться в упорядоченном списке и вставляем его туда
Блочная сортировка (Корзинная сортировка, Bucket sort) — Сложность алгоритма: O(n); требуется O(k) дополнительной памяти и знание о природе сортируемых данных, выходящее за рамки функций "переставить" и "сравнить".
Сортировка подсчётом (Counting sort) — Сложность алгоритма: O(n+k); требуется O(n+k) дополнительной памяти (рассмотрено 3 варианта)
Сортировка слиянием (Merge sort) — Сложность алгоритма: O(n log n); требуется O(n) дополнительной памяти; выстраиваем первую и вторую половину списка отдельно, а затем — сливаем упорядоченные списки
Сортировка с помощью двоичного дерева (англ. Tree sort) — Сложность алгоритма: O(n log n); требуется O(n) дополнительной памяти
Слайд 8Алгоритмы неустойчивой сортировки
Сортировка выбором (Selection sort) — Сложность алгоритма: O(n2); поиск
наименьшего или наибольшего элемента и помещения его в начало или конец упорядоченного списка
Сортировка Шелла (Shell sort) — Сложность алгоритма: O(n log2 n); попытка улучшить сортировку вставками
Сортировка расчёской (Comb sort) — Сложность алгоритма: O(n log n)
Пирамидальная сортировка (Сортировка кучи, Heapsort) — Сложность алгоритма: O(n log n); превращаем список в кучу, берём наибольший элемент и добавляем его в конец списка
Плавная сортировка (Smoothsort) — Сложность алгоритма: O(n log n)
Быстрая сортировка (Quicksort) — Сложность алгоритма: O(n log n) — среднее время, O(n2) — худший случай;
Поразрядная сортировка (Цифровая сортировка) — Сложность алгоритма: O(n·k); требуется O(k) дополнительной памяти.
Сортировка Шелла (Shell sort) — Сложность алгоритма: O(n log2 n); попытка улучшить сортировку вставками
Сортировка расчёской (Comb sort) — Сложность алгоритма: O(n log n)
Пирамидальная сортировка (Сортировка кучи, Heapsort) — Сложность алгоритма: O(n log n); превращаем список в кучу, берём наибольший элемент и добавляем его в конец списка
Плавная сортировка (Smoothsort) — Сложность алгоритма: O(n log n)
Быстрая сортировка (Quicksort) — Сложность алгоритма: O(n log n) — среднее время, O(n2) — худший случай;
Поразрядная сортировка (Цифровая сортировка) — Сложность алгоритма: O(n·k); требуется O(k) дополнительной памяти.
Слайд 9Прочие алгоритмы сортировки
Сортировка перестановкой — O(n·n!) — худшее время. Для каждой
пары осуществляется проверка верного порядка и генерируются всевозможные перестановки исходного массива.
Глупая сортировка (Stupid sort) — O(n3); рекурсивная версия требует дополнительно O(n2) памяти
Блинная сортировка (Pancake sorting) — O(n), требуется специализированное аппаратное обеспечение
Лексикографическая или поразрядная сортировка (Radix sort)
Сортировка подсчётом (Counting sort)
Топологическая сортировка
Внешняя сортировка
Глупая сортировка (Stupid sort) — O(n3); рекурсивная версия требует дополнительно O(n2) памяти
Блинная сортировка (Pancake sorting) — O(n), требуется специализированное аппаратное обеспечение
Лексикографическая или поразрядная сортировка (Radix sort)
Сортировка подсчётом (Counting sort)
Топологическая сортировка
Внешняя сортировка
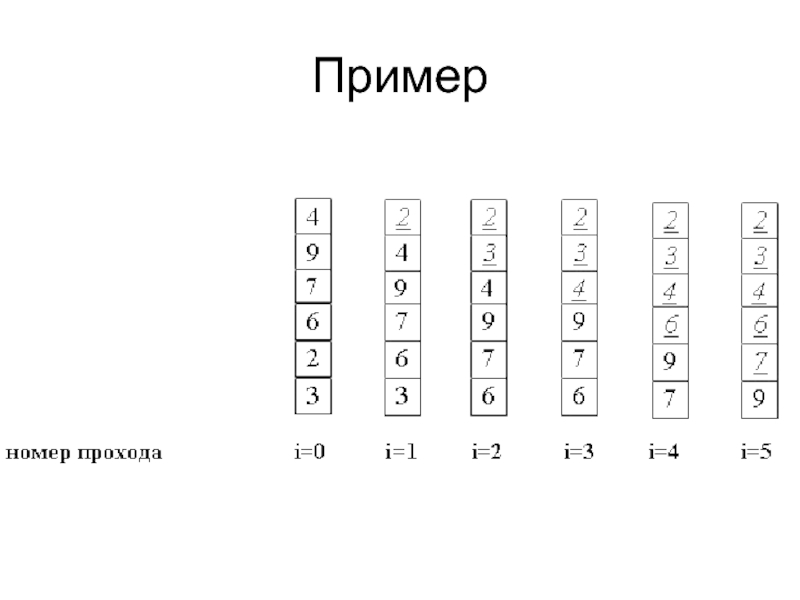
Слайд 10Сортировка обменом (пузырьковая сортировка)
Идея метода: шаг сортировки состоит в проходе снизу
вверх по массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами.
Слайд 13Сортировка «пузырьком»
for (int i = 1; i < n;
i++) {
for (int j = 0; j < n-i; j++) {
if (data[j] > data [j+1]) {
int tmp = data[j];
data[j] = data[j+1];
data[j+1] = tmp;
}
}
}
for (int j = 0; j < n-i; j++) {
if (data[j] > data [j+1]) {
int tmp = data[j];
data[j] = data[j+1];
data[j+1] = tmp;
}
}
}
Слайд 14Оптимизация алгоритма
Запоминаем, производился ли на данном проходе какой-либо обмен. Если нет
- алгоритм заканчивает работу.
Запоминаем индекс последнего обмена k. Действительно: все пары соседих элементов с индексами, меньшими k, уже расположены в нужном порядке. Дальнейшие проходы можно заканчивать на индексе k, вместо того чтобы двигаться до установленной заранее верхней границы i.
Меняем направление следующих один за другим проходов. Получившийся алгоритм иногда называют "шейкер-сортировкой".
Запоминаем индекс последнего обмена k. Действительно: все пары соседих элементов с индексами, меньшими k, уже расположены в нужном порядке. Дальнейшие проходы можно заканчивать на индексе k, вместо того чтобы двигаться до установленной заранее верхней границы i.
Меняем направление следующих один за другим проходов. Получившийся алгоритм иногда называют "шейкер-сортировкой".
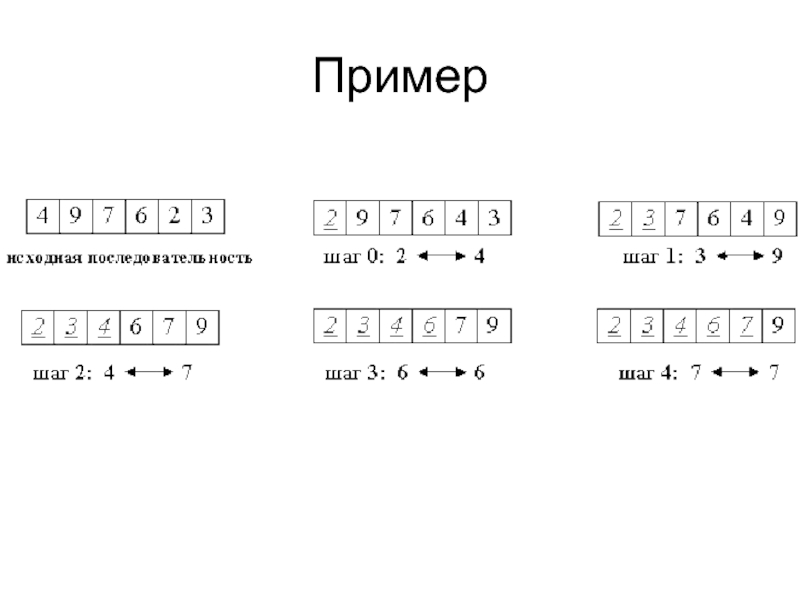
Слайд 15Сортировка выбором
Идея метода состоит в том, чтобы создавать отсортированную последовательность путем
присоединения к ней одного элемента за другим в правильном порядке.
Суть алгоритма: Построить готовую упорядоченную последовательность, начиная с левого конца массива.
Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м.
На i-м шаге выбираем наименьший из элементов a[i] ... a[n] и меняем его местами с a[i].
Суть алгоритма: Построить готовую упорядоченную последовательность, начиная с левого конца массива.
Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м.
На i-м шаге выбираем наименьший из элементов a[i] ... a[n] и меняем его местами с a[i].
Слайд 17Сортировка вставками
Идея алгоритма: Предположим последовательность a[0]...a[i] упорядочена. При этом по ходу
алгоритма в нее будут вставляться все новые элементы.
Суть алгоритма: На i-м шаге последовательность разделена на две части: готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n].
На следующем, (i+1)-м каждом шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива. Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним. В зависимости от результата сравнения элемент либо остается на текущем месте(вставка завершена), либо они меняются местами и процесс повторяется.
Суть алгоритма: На i-м шаге последовательность разделена на две части: готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n].
На следующем, (i+1)-м каждом шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива. Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним. В зависимости от результата сравнения элемент либо остается на текущем месте(вставка завершена), либо они меняются местами и процесс повторяется.
Слайд 19Сортировка простыми вставками
1
3
4
8
10
14
16
21
24
31
33
36
38
42
44
50
53
59
1
3
4
8
10
14
16
21
24
31
33
36
38
42
44
50
27
51
53
59
1
3
4
8
10
14
16
21
24
31
33
36
38
42
44
50
27
51
53
59
1
3
8
10
16
21
24
33
36
38
44
50
53
59
int i, j;
for (i = 1; i
< n; i++) {
int c = data[i];
for (j = i-1; j >= 0 && data[j] > c; j--) {
data[j+1] = data[j];
}
data[j+1] = c;
}
int c = data[i];
for (j = i-1; j >= 0 && data[j] > c; j--) {
data[j+1] = data[j];
}
data[j+1] = c;
}
Слайд 20Сортировка Шелла
Сортировка Шелла (англ. Shell sort) — алгоритм сортировки, идея которого состоит в
сравнении элементов, стоящих не только рядом, но и на расстоянии друг от друга. Иными словами — сортировка вставками с предварительными «грубыми» проходами.
При сортировке Шелла сначала сравниваются и сортируются между собой ключи, отстоящие один от другого на некотором расстоянии d. После этого процедура повторяется для некоторых меньших значений d, а завершается сортировка Шелла упорядочиванием элементов при d = 1 (то есть, обычной сортировкой вставками).
При сортировке Шелла сначала сравниваются и сортируются между собой ключи, отстоящие один от другого на некотором расстоянии d. После этого процедура повторяется для некоторых меньших значений d, а завершается сортировка Шелла упорядочиванием элементов при d = 1 (то есть, обычной сортировкой вставками).
Слайд 21Сортировка Шелла
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
0
step=7
1
3
4
8
10
14
16
21
24
31
33
36
38
42
44
50
27
51
53
59
step=3
step=2
step=1
Слайд 22Сортировка Шелла
int n ; // Длина массива
int step
= n; // Шаг поисков и вставки
int i, j;
do {
// Вычисляем новый шаг
step = step / 3 + 1;
// Производим сортировку простыми вставками с заданным шагом
for (i = step; i < n; i++) {
int c = data[i];
for (j = i-step; j >= 0 && data[j] > c; j -= step) {
data[j+step] = data[j];
}
data[j+step] = c;
}
} while (step != 1);
int i, j;
do {
// Вычисляем новый шаг
step = step / 3 + 1;
// Производим сортировку простыми вставками с заданным шагом
for (i = step; i < n; i++) {
int c = data[i];
for (j = i-step; j >= 0 && data[j] > c; j -= step) {
data[j+step] = data[j];
}
data[j+step] = c;
}
} while (step != 1);
Количество перестановок элементов
(по результатам экспериментов со случайным массивом)
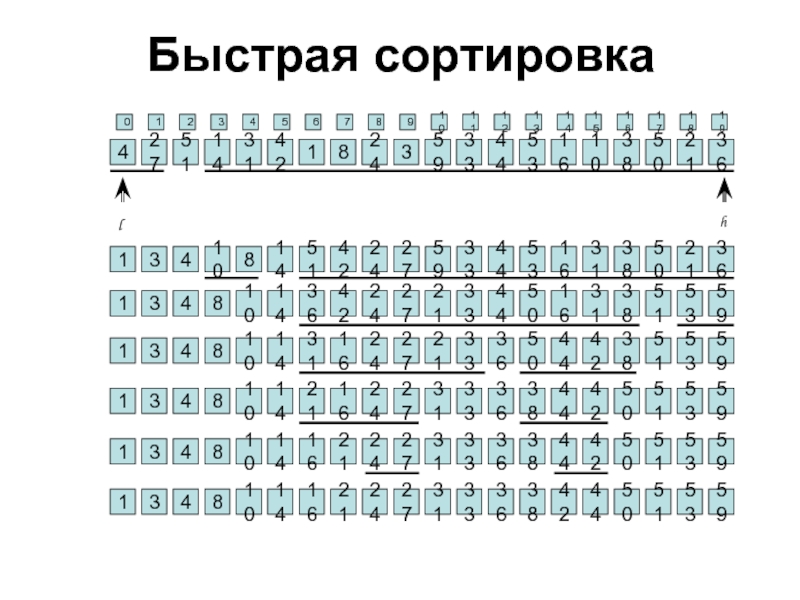
Слайд 23Быстрая сортировка
Быстрая сортировка (англ. quicksort) — широко известный алгоритм сортировки, разработанный английским
информатиком Чарльзом Хоаром. Один из быстрых известных универсальных алгоритмов сортировки массивов (в среднем O(n log n) обменов при упорядочении n элементов), хотя и имеющий ряд недостатков.
Краткое описание алгоритма
выбрать элемент, называемый опорным.
сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие-равные-большие.
повторить рекурсивно для «меньших» и «больших».
Краткое описание алгоритма
выбрать элемент, называемый опорным.
сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие-равные-большие.
повторить рекурсивно для «меньших» и «больших».
Слайд 26Дополнения и улучшения алгоритма
Первый элемент в сортируемом куске выбирается случайно и
запоминается;
Участки, меньшие определенного размера, сортируются простыми способами;
Иногда исключение рекурсивных вызовов приводит к повышению эффективности.
Участки, меньшие определенного размера, сортируются простыми способами;
Иногда исключение рекурсивных вызовов приводит к повышению эффективности.
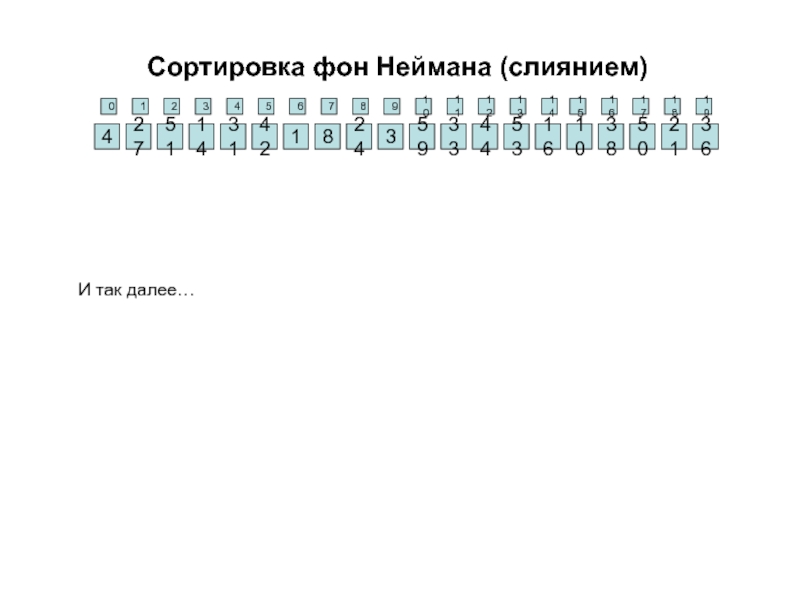
Слайд 27Алгоритм слияния упорядоченных массивов
1
3
4
8
14
24
31
42
27
51
59
int na, // длина массива a[]
nb, // длина массива b[]
nc;
int[] c = new int[nc = na + nb];
int ia = 0,
ib = 0,
ic = 0;
while (ia < na && ib < nb) {
if (a[ia] < b[ib])
c[ic++] = a[ia++];
else
c[ic++] = b[ib++];
}
while (ia < na) c[ic++] = a[ia++];
while (ib < nb) c[ic++] = b[ib++];
nc;
int[] c = new int[nc = na + nb];
int ia = 0,
ib = 0,
ic = 0;
while (ia < na && ib < nb) {
if (a[ia] < b[ib])
c[ic++] = a[ia++];
else
c[ic++] = b[ib++];
}
while (ia < na) c[ic++] = a[ia++];
while (ib < nb) c[ic++] = b[ib++];
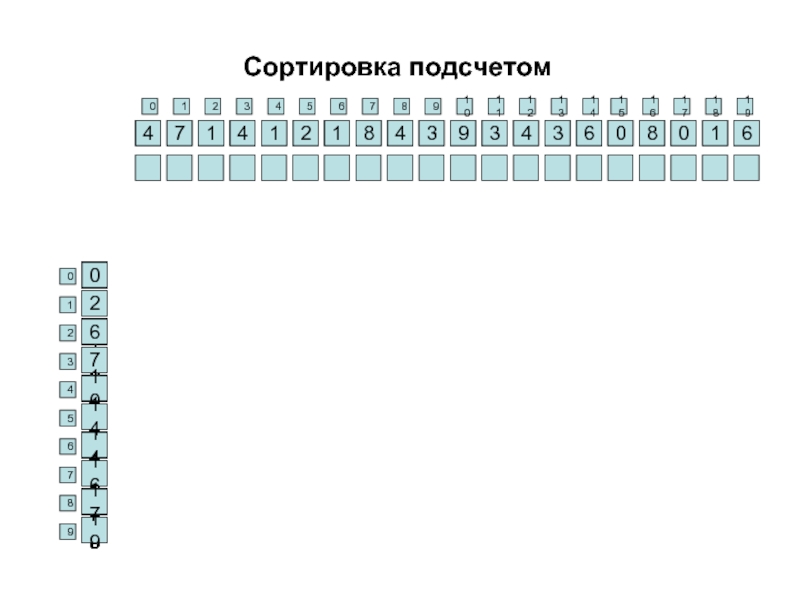
Слайд 29Сортировка подсчетом
Этот алгоритм подходит для сортировки целых чисел из не очень
большого диапазона (сравнимого с размером массива).
Идея алгоритма: для каждого элемента найти, сколько элементов, меньших определенного числа, и поместить это число на соответствующие место. За линейный проход по массиву для каждого из возможных значений подсчитываем, сколько элементов имеют такое значение. Потом добавляем к каждому из найденных чисел суму всех предыдущих. Получая, таким образом, сколько есть элементов, значения которых не больше данного значения. Далее, опять-таки за линейный проход, формируем из исходного массива новый отсортированный.
Идея алгоритма: для каждого элемента найти, сколько элементов, меньших определенного числа, и поместить это число на соответствующие место. За линейный проход по массиву для каждого из возможных значений подсчитываем, сколько элементов имеют такое значение. Потом добавляем к каждому из найденных чисел суму всех предыдущих. Получая, таким образом, сколько есть элементов, значения которых не больше данного значения. Далее, опять-таки за линейный проход, формируем из исходного массива новый отсортированный.
Слайд 31Цифровая сортировка
Цифровая сортировка — один из алгоритмов сортировки, использующих внутреннюю структуру
сортируемых объектов. Алгоритм состоит в последовательной сортировке объектов какой-либо устойчивой сортировкой по каждому разряду, в порядке от младшего разряда к старшему, после чего последовательности будут расположены в требуемом порядке.
Слайд 33Алгоритмы поиска
Одно из наиболее часто встречающихся в программировании действий это- поиск.
Существует несколько основных вариантов поиска, и для них создано много различных алгоритмов.
Слайд 34Линейный поиск
Данный алгоритм является простейшим алгоритмом поиска и в отличие, например,
от двоичного поиска, не накладывает никаких ограничений на функцию и имеет простейшую реализацию. Поиск значения функции осуществляется простым сравнением очередного рассматриваемого значения (как правило поиск происходит слева направо, т.е. от меньших значений аргумента к большим) и, если значения совпадают (с той или иной точностью), то поиск считается завершённым.
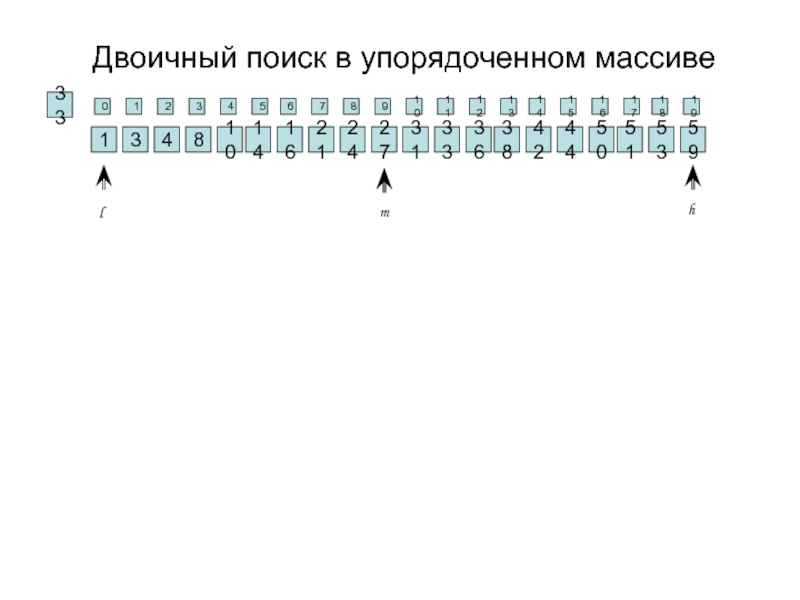
Слайд 35Двоичный поиск
Двоичный поиск (также известен, как метод деления пополам и метод
половинного деления) — алгоритм нахождения заданного значения монотонной (невозрастающей или неубывающей) функции. Поиск основывается на теореме о промежуточных значениях. Используется в информатике, вычислительной математике и математическом программировании.
Слайд 36Двоичный поиск в упорядоченном массиве
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
0
1
3
4
8
10
14
16
21
24
27
31
33
36
38
42
44
50
51
53
59
33
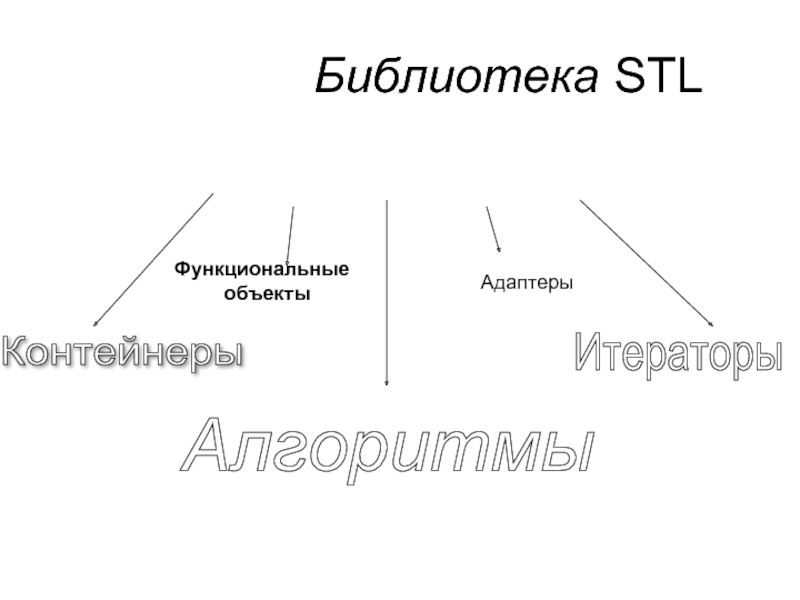
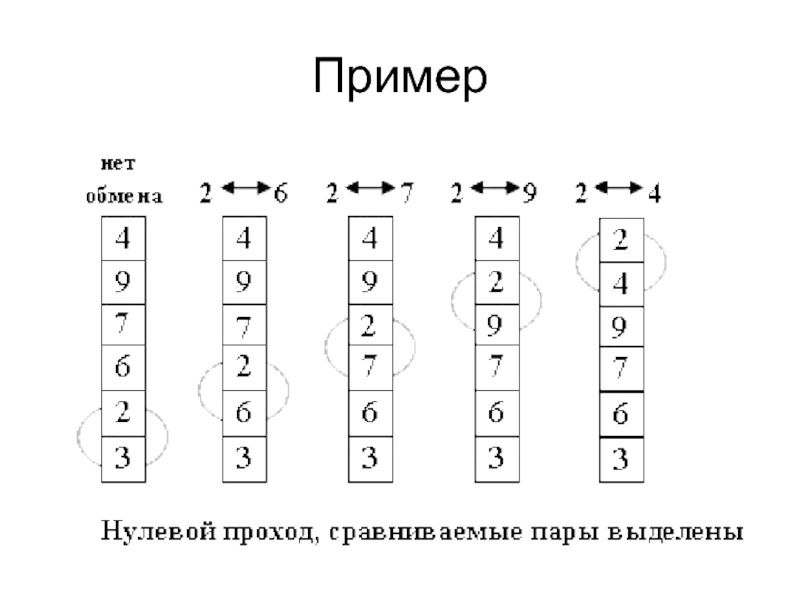
Слайд 38Алгоритмы STL
STL - алгоритмы представляют набор готовых функций, которые могут быть
применены к STL коллекциям и могут быть подразделены на три основных группы
Поиска
Математические
Сортировки
Работы
С последовательностями
Слайд 39Функции для сортировки членов коллекции
sort, stable_sort, partial_sort, partial_sort_copy, nth_element, binary_search, lower_bound,
upper_bound, equal_range, merge, inplace_merge, includes, set_union, set_intersection, set_difference, set_symmetric_difference, make_heap, push_heap, pop_heap, sort_heap, min, max, min_element, max_element, lexographical_compare, next_permutation, prev_permutation













![Сортировка вставкамиИдея алгоритма: Предположим последовательность a[0]...a[i] упорядочена. При этом по ходу алгоритма в нее будут](/img/tmb/2/117603/9866f4fd7ac82864c5c0fe220705ee24-800x.jpg)







![Алгоритм слияния упорядоченных массивов134814243142275159 int na, // длина массива a[] nb, // длина массива](/img/tmb/2/117603/dc62313df14349d5edc5c90ab8b5d910-800x.jpg)