- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления презентация
Содержание
- 1. Системы счисления
- 2. Системы счисления Известно много способов представления чисел.
- 3. Непозиционные системы счисления Непозиционные – значение каждой
- 4. Примеры (продолжение) Система счисления Древнего Египта
- 5. Примеры (продолжение) Славянская нумерация (или алфавитная) –
- 6. Позиционные системы счисления Позиционные – значение цифры
- 7. Другие системы Двенадцатиричная система счисления. Происхождение ее
- 8. Пятиричная система счисления (связано с рукой)
- 9. Древнегреческая нумерация – числа 1, 2,
- 10. К позиционным системам счисления относятся и
- 11. Двоичная система счисления Из всех позиционных систем
- 12. Примеры Пример 1, некогда был пруд, в
- 13. Двоичная арифметика С двоичными числами, как
- 14. Вычитание Вычитание. Правила вычитания: 0 –
- 15. Умножение Правила умножения: 0 • 0 =
- 16. Задание Задание. Воспользуйтесь формулой для перевода
- 17. Системы счисления, используемые в компьютере Кроме
- 18. Перевод чисел из одной системы счисления в
- 19. Общее правило перевода целых чисел из системы
- 20. Деление Деление в двоичной системе счисления, как
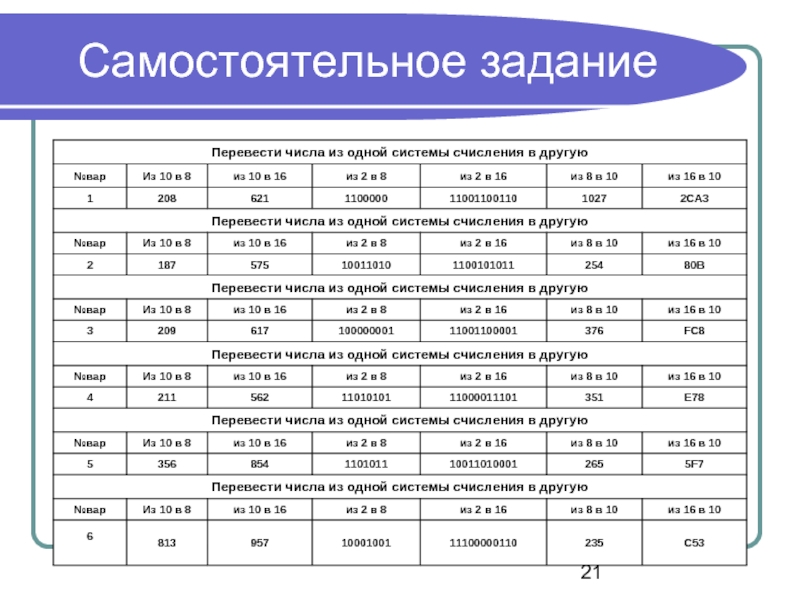
- 21. Самостоятельное задание
Слайд 1Системы счисления
Системы счисления
Двоичная система счисления
Двоичная арифметика
Системы счисления, используемые
Слайд 2Системы счисления
Известно много способов представления чисел.
В любом случае число изображается
Будем называть такие символы цифрами,
символические изображения чисел – кодами,
правила получения кодов – системами счисления, которые делятся на непозиционные и позиционные.
Слайд 3Непозиционные системы счисления
Непозиционные – значение каждой цифры не зависит от ее
Примеры:
унарная система – для записи чисел используется всего один символ (палочка, узелок, зарубка, камушек), длина записи числа при таком кодировании связана с его величиной;
римская система счисления;
I (1), V (5), X (10), L (50), C (100), D (500), M (1000),
III (3), IV (4), VI (6), XL (40), LX (60), XC (90), CIX (109)
MCMLXXXVI = 1986
Слайд 4Примеры (продолжение)
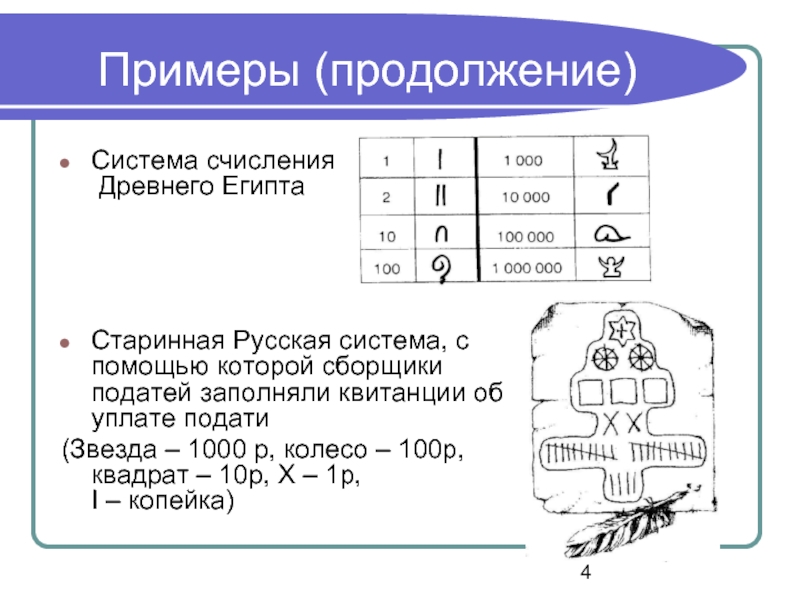
Система счисления
Древнего Египта
Старинная Русская система, с помощью которой
(Звезда – 1000 р, колесо – 100р, квадрат – 10р, Х – 1р, I – копейка)
Слайд 5Примеры (продолжение)
Славянская нумерация (или алфавитная) – числовые значения букв устанавливались в
Слайд 6Позиционные системы счисления
Позиционные – значение цифры зависит от ее места в
В привычной нам системе счисления для записи чисел используются 10 различных знаков. Причина, по которой десятичная система стала общепринятой – 10 пальцев на руке (вот аппарат для счета, которым человек пользуется с доисторических времен. Древнее написание
Каждая цифра обозначает количество углов в ней: 0 – углов нет, 1 – один угол, 2 – два угла и т.д. Десятичной системой люди пользовались не всегда. В разные исторические периоды многие народы использовали другие системы счисления.
Слайд 7Другие системы
Двенадцатиричная система счисления. Происхождение ее тоже связано со счетом на
Мы сталкиваемся с двенадцатиричной системой – сервиз на 12 персон, мебель (12 стульев), циферблат часов и т.д.
Слайд 8
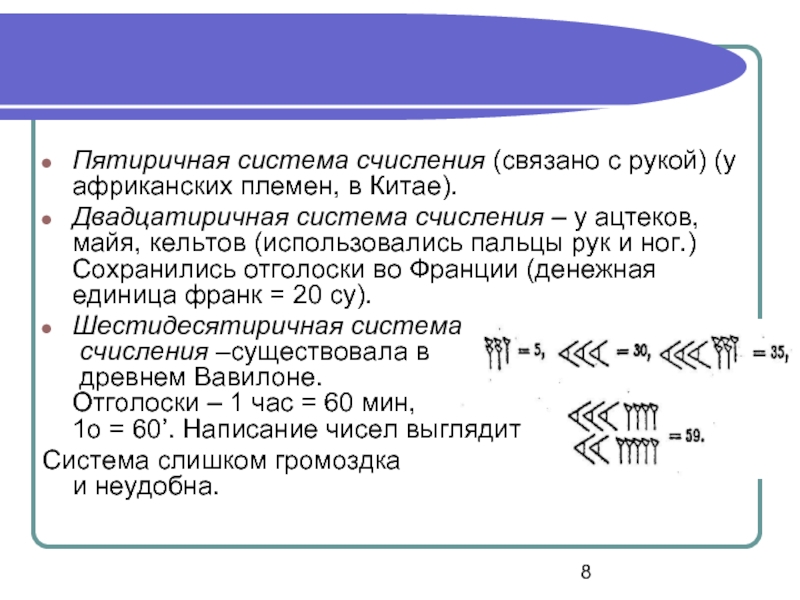
Пятиричная система счисления (связано с рукой) (у африканских племен, в Китае).
Двадцатиричная
Шестидесятиричная система счисления –существовала в древнем Вавилоне. Отголоски – 1 час = 60 мин, 1о = 60’. Написание чисел выглядит
Система слишком громоздка и неудобна.
Слайд 9
Древнегреческая нумерация – числа 1, 2, 3, 4 обозначались черточками |,
Слайд 10
К позиционным системам счисления относятся и «машинные» системы счисления: двоичная, восьмеричная
Из истории известен курьезный случай с восьмеричной системой. Шведский король Карл XII в 1717 году увлекался восьмеричной системой, считал ее более удобной, чем десятичная, и намеревался королевским указом ввести ее как общепринятую. Неожиданная смерть короля помешала ему осуществить столь необычное намерение
Слайд 11Двоичная система счисления
Из всех позиционных систем счисления двоичная
особенно проста. Следует
Итак, двоичное число представляет собой цепочку из нулей и единиц. Обычно у него достаточно большое число разрядов. Быстрый рост числа разрядов – самый существенный недостаток двоичной системы счисления.
Слайд 12Примеры
Пример 1, некогда был пруд, в центре которого рос один лист
Пример 2, на одном из приисков старатели были возмущены действиями Джо Макдональда – хозяина салуна, принимавшего от них в уплату золотой песок. Очень уж необычными были гири, с помощью которых тот взвешивал золото: 1, 2. 4, 8, 16, 32, и 64 грамма. Джо утверждал, что с помощью такого набора гирь он может взвесить любую порцию песка, не превышающую 127 граммов. Прав ли Джо? Какой наибольший вес могут «взять» такие гири? Как с помощью названных гирь набрать вес: 25 г., 48 г., 72 г., 105 г. ? Джо прав – 10010 = 11001002 , максимальный вес составляет 11111112 = 127 г
Слайд 13Двоичная арифметика
С двоичными числами, как и с десятичными можно производить
Сложение. Правила сложения:
0 + 0 = 0
0 + 1 = 1
1 + 0 =1
1 + 1 = 10 – результат сложения двух единиц: ноль и единица переноса в старший разряд – 1 основное правило двоичной системы счисления.
Пример. Сложить два двоичных числа 1101112 и 10112 (двойка, записанная справа от числа указывает на двоичную систему счисления). Далее будем пользоваться аналогичным обозначением и для других систем счисления. Складывать будем столбиком: 1101112
+
10112
--------
10000102
Слайд 14Вычитание
Вычитание. Правила вычитания: 0 – 0 = 0
1 – 1 =0
10 – 1 = 1 – второе основное правило двоичной системы счисления.
При вычитании многоразрядных чисел может возникнуть необходимость «занять» единицу в старшем разряде, что дает две единицы в младшем разряде. Нужно отметить, что если в десятичном числе выделяются разряды единиц, сотен и т.д., то в двоичном числе выделяются разряды единиц, двоек, четверок…
Пример: 1002 - 112. В числе 1002 выделим следующие разряды:
1 - разряд четверок;
0 – разряд двоек;
0 – разряд единиц.
Вычесть единицу из младшего разряда (единиц) нельзя, перейдем к следующему разряду (двоек),но и тут тоже ноль, поэтому перейдем к следующему разряду (четверок). Находящуюся в этом разряде единицу представим как сумму двух единиц из разряда двоек, т.е.
теперь одну из полученных единиц также представим как сумму единиц младшего разряда (в разряде двоек останется одна единица), т.е.
легко выполнить вычитание из уменьшаемого, записанного в таком виде:
Как и в десятичной системе проверить вычитание можно обратным действием – сложением.
Слайд 15Умножение
Правила умножения:
0 • 0 = 0
0 • 1 = 0
1 •
1 • 1 = 1
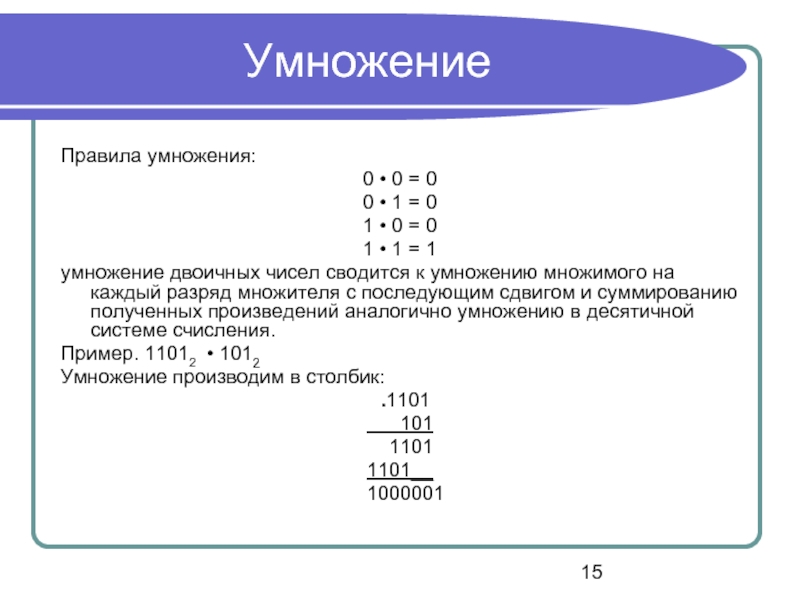
умножение двоичных чисел сводится к умножению множимого на каждый разряд множителя с последующим сдвигом и суммированию полученных произведений аналогично умножению в десятичной системе счисления.
Пример. 11012 • 1012
Умножение производим в столбик:
.1101
101
1101
1101__
1000001
Слайд 16Задание
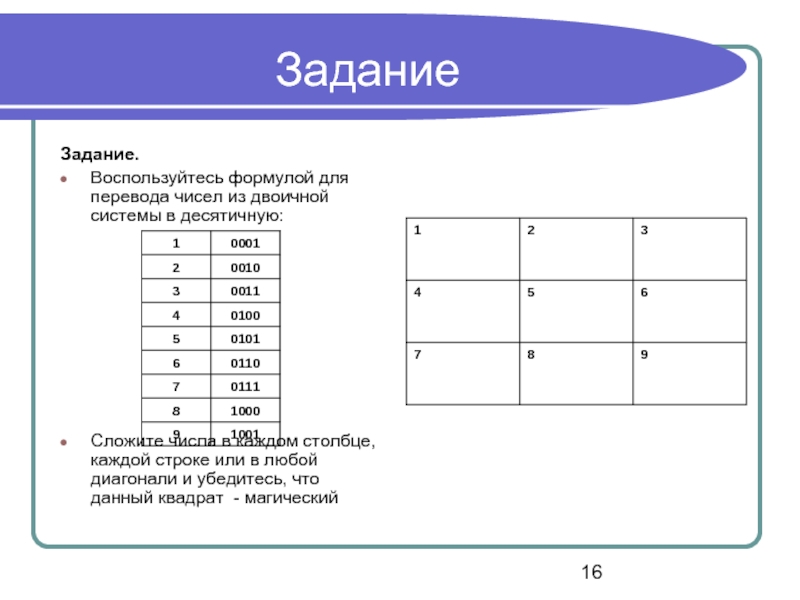
Задание.
Воспользуйтесь формулой для перевода чисел из двоичной системы в десятичную:
Сложите
Слайд 17Системы счисления, используемые в компьютере
Кроме двоичной системы в компьютере также
Обмен информацией между устройствами большинства ЭВМ осуществляется путем передачи двоичных чисел.
Пользоваться такими числами из-за большой их длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты и инженеры) на этапах составления программ, их отладки часто заменяют двоичные коды на восьмеричные или шестнадцатиричные.
В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
Слайд 18Перевод чисел из одной системы счисления в другую
Пример 1. Перевести
Собирая остатки от деления в направлении, указанном стрелкой, получим 1910 = 100112
Пример 2. Перевести десятичное число 173 в восьмеричную систему счисления.
Снова собираем остатки от деления в направлении стрелки, получаем 17310 = 2558
Пример 3. Перевести десятичное число 173 в шестнадцатиричную систему счисления: (используются цифры от 0 до 9, а затем афавит 10 – А, 11 – B, 12 – C, 13 – D, 14 – E, 15 – F)
Слайд 19Общее правило перевода целых чисел из системы счисления с основанием р
последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя,
полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления,
составить число в новой системе счисления, записывая его начиная с последнего остатка.
Перевод числа из двоичной, восьмеричной, шестнадцатиричной системы:
Слайд 20Деление
Деление в двоичной системе счисления, как и в десятичной, основано на
Пример. Разделить число 10101 на число 111
10101 |111
111 11
111
111
0