- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рекурсия. Сортировка слиянием. Восходящая сортировка слиянием. Сложность сортировки. Устойчивость сортировок презентация
Содержание
- 1. Рекурсия. Сортировка слиянием. Восходящая сортировка слиянием. Сложность сортировки. Устойчивость сортировок
- 2. Пример бесконечной рекурсии У попа была собака,
- 3. Рекурсивная функция function arifmPr(base, iter: integer): integer;
- 4. Рекурсивная функция arifmPr(2, 4) arifmPr:= arifmPr(2,3)+2 arifmPr:=
- 5. Сортировка слиянием (Mergesort)
- 6. Два классических алгоритма сортировки Критические компоненты в
- 7. Сортировка слиянием Основной план Разделить массив на
- 8. Сортировка слиянием Цель. Получить два отсортированных подмассива
- 9. Слияние: реализация на Java
- 10. Assertions Assertion. Оператор для тестирования программы Помогает
- 11. Сортировка слиянием: реализация на Java
- 12. Сортировка слиянием: трассировка
- 13. Видео 2
- 14. Сортировка слиянием: эмпирический анализ Оценка времени выполнения:
- 15. Сортировка слиянием: количество сравнений и обращений к
- 16. Разделяй и властвуй Утверждение. Если D(N) удовлетворяет
- 17. Разделяй и властвуй Утверждение. Если D(N) удовлетворяет
- 18. Разделяй и властвуй Утверждение. Если D(N) удовлетворяет
- 19. Анализ сортировки слиянием: память Утверждение. Сортировка слиянием
- 20. Сортировка слиянием: реализация Используйте сортировку вставками для
- 21. Сортировка слиянием: реализация Остановка если все отсортировано Если самый большой элемент первой половины
- 22. Сортировка слиянием: реализация Ограничить копирование во вспомогательный
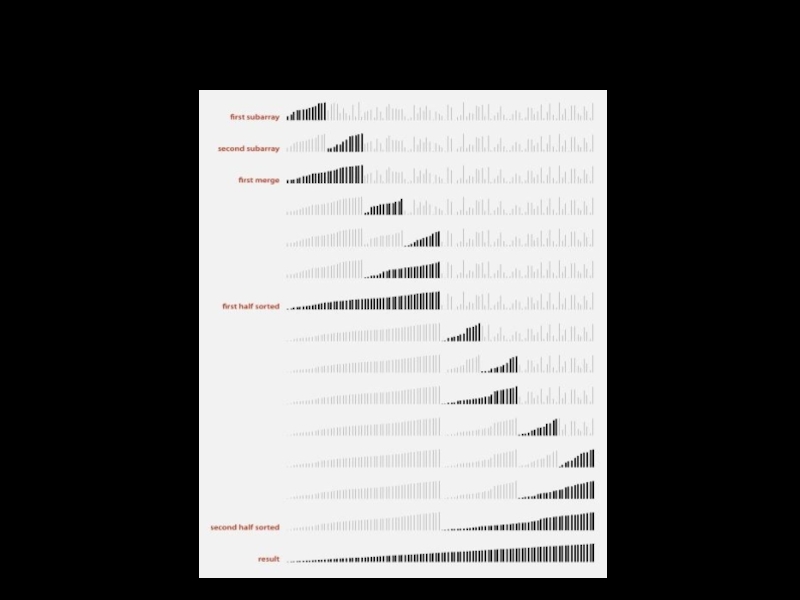
- 23. Сортировка слиянием: визуализация
- 24. Восходящая сортировка слиянием (Bottom-up mergesort)
- 25. Восходящая сортировка слиянием Начинаем со слияния подмассивов
- 26. Восходящая сортировка слиянием: реализация на Java Итог.
- 27. Восходящая сортировка слиянием: визуализация
- 28. Сложность сортировки
- 29. Сложность сортировки Вычислительная сложность - основа для
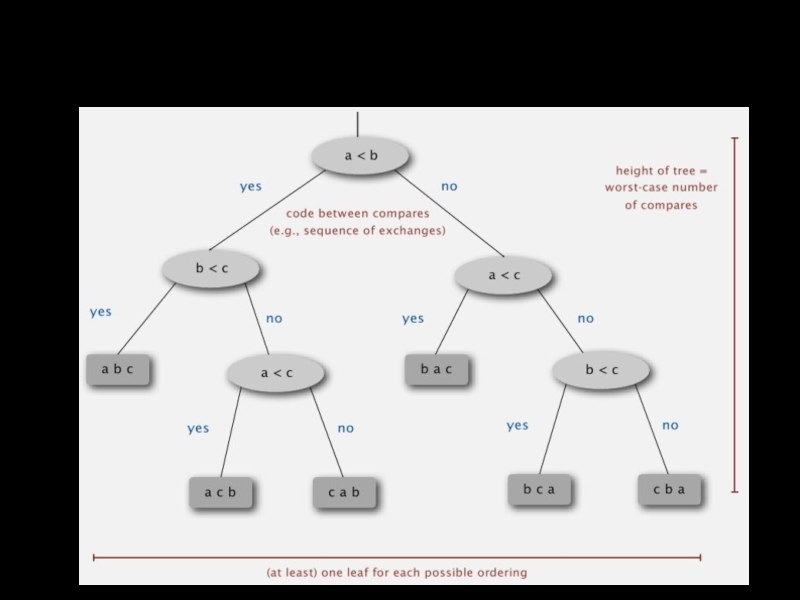
- 30. Дерево принятия решений (для 3-х элементов)
- 31. Нижняя граница для сортировки на основе сравнений
- 32. Нижняя граница для сортировки на основе сравнений
- 33. Сложность сортировки Вычислительная модель. Возможные операции Стоимость
- 34. Сложность сортировки Сравнения? Сортировка слиянием оптимальна по
- 35. Сложность сортировки Можно снизить нижнюю границу для
- 36. Устойчивость сортировок
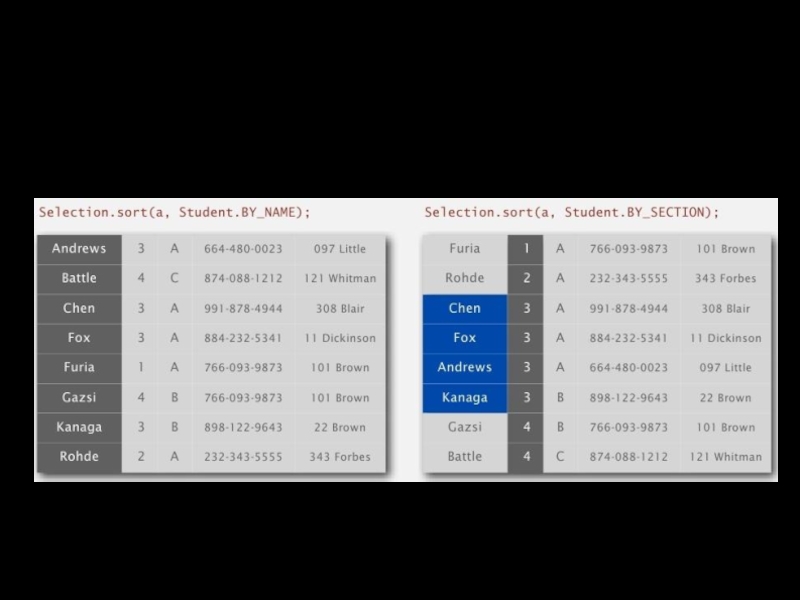
- 37. Устойчивость Типичная задача. Отсортировать сначала по имени,
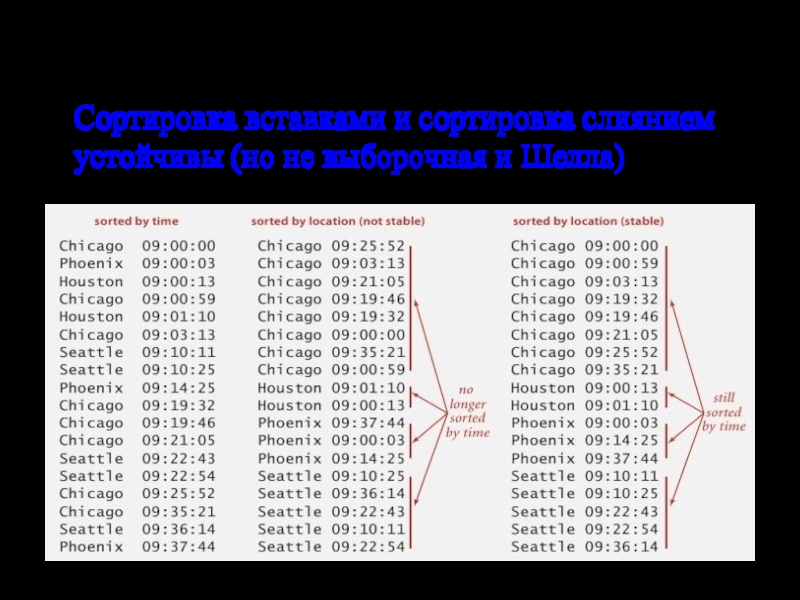
- 38. Устойчивость Сортировка вставками и сортировка слиянием устойчивы (но не выборочная и Шелла)
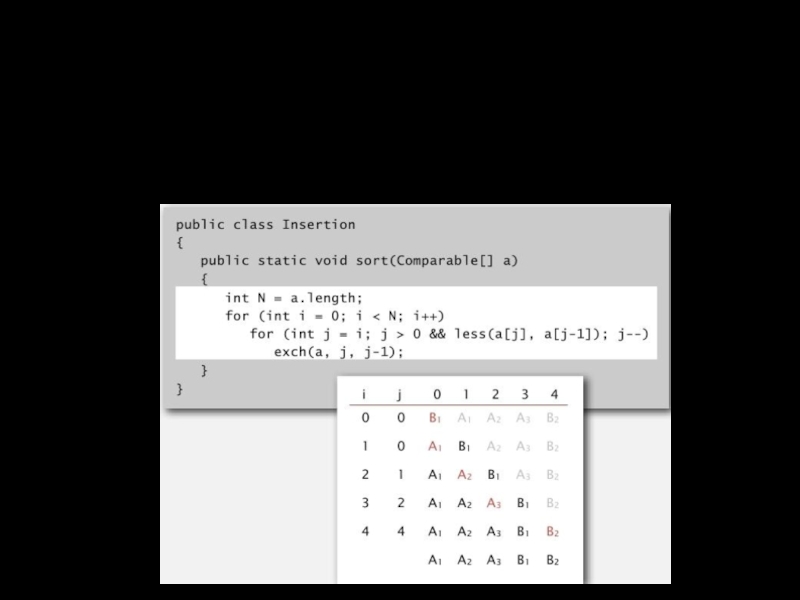
- 39. Устойчивость: сортировка вставками Сортировка вставками устойчива Равные элементы не передвигаются
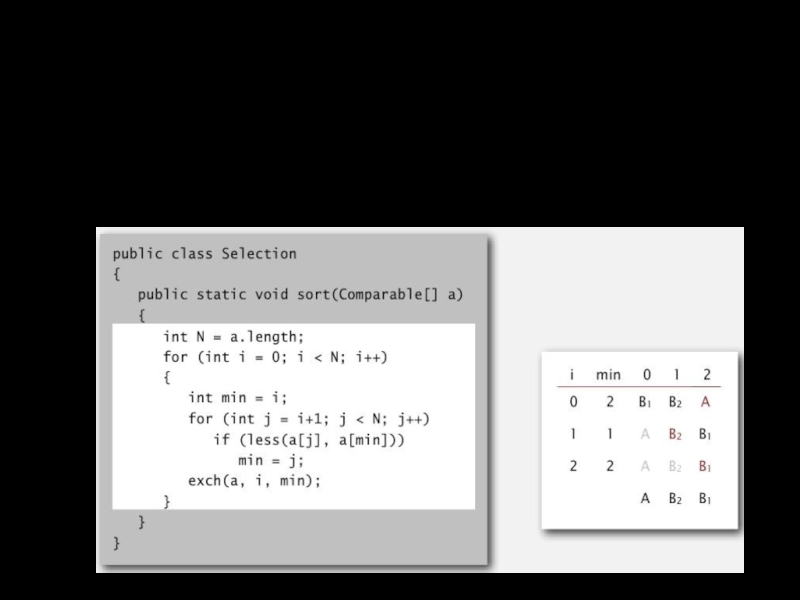
- 40. Устойчивость: выборочная сортировка Выборочная сортировка не устойчива Передвижения элементов на большие расстояния может нарушить порядок
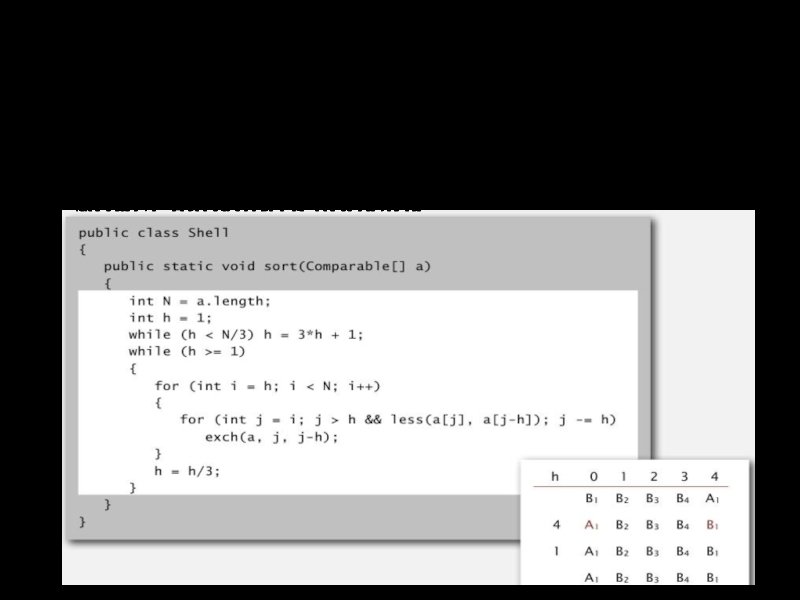
- 41. Устойчивость: сортировка Шелла Сортировка Шелла не устойчива Передвижения элементов на большие расстояния может нарушить порядок
- 42. Устойчивость: сортировка слиянием Сортировка слиянием устойчива Если ключи равны, то берутся элементы из левого подмассива
Слайд 2Пример бесконечной рекурсии
У попа была собака, он её любил,
Она съела кусок
В землю закопал,
Надпись написал:
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
Слайд 3Рекурсивная функция
function arifmPr(base, iter: integer): integer;
begin
if iter = 1 then
else
arifmPr:= arifmPr(base, iter - 1) + base;
end;
Слайд 4Рекурсивная функция
arifmPr(2, 4)
arifmPr:= arifmPr(2,3)+2
arifmPr:= 8+2
arifmPr:= arifmPr(2,2)+2
arifmPr:= 6+2
arifmPr(2, 3)
arifmPr:= arifmPr(2,2)+2
arifmPr:= 4+2
arifmPr(2, 2)
arifmPr:= arifmPr(2,1)+2
arifmPr:= 2+2
arifmPr(2, 1)
arifmPr:= 2
Слайд 6Два классических алгоритма сортировки
Критические компоненты в мировой вычислительной инфраструктуре
Понимание научных основ
Быстрая сортировка входит в десятку самых полезных алгоритмов, разработанных в 20-м веке
Слайд 7Сортировка слиянием
Основной план
Разделить массив на две половины
Рекурсивно отсортировать каждую половину
Соединить две
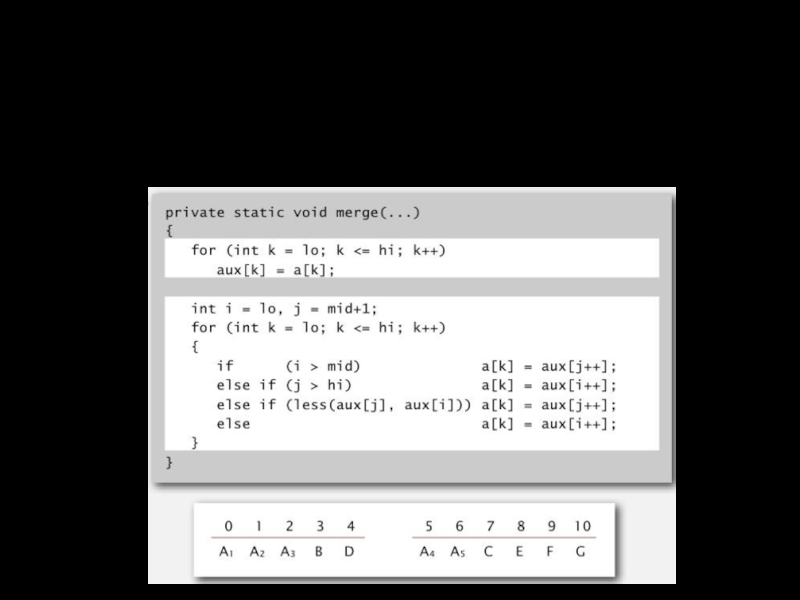
Слайд 8Сортировка слиянием
Цель. Получить два отсортированных подмассива от a[lo] до a[mid] и
Видео 1
Слайд 10Assertions
Assertion. Оператор для тестирования программы
Помогает обнаружить логические ошибки
Документирует код
Java assert оператор.
Можно включать и выключать в процессе работы => не влияет на производительность в процессе работы
Лучшие варианты использования. Использовать для проверки инвариантов. Отключать в отлаженном коде
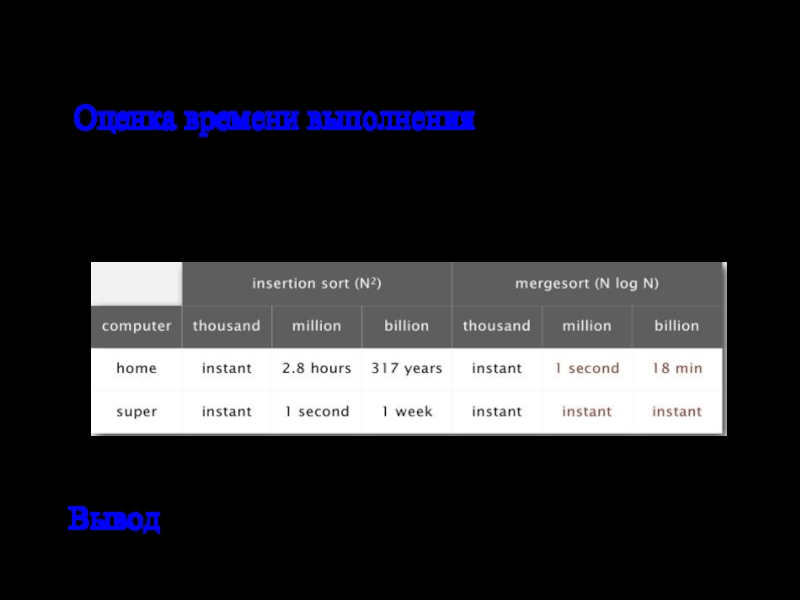
Слайд 14Сортировка слиянием: эмпирический анализ
Оценка времени выполнения:
На ПК 108 сравнений/секунду
На суперкомпьютере 1012
Вывод. Хорошие алгоритмы лучше, чем суперкомпьютер
Слайд 15Сортировка слиянием: количество сравнений и обращений к массиву
Утвержение. Сортировка слиянием использует
Доказательство. C(N) — количество сравнений, A(N) — количество обращений
Решим рекуррентность для N. N — степень двойки
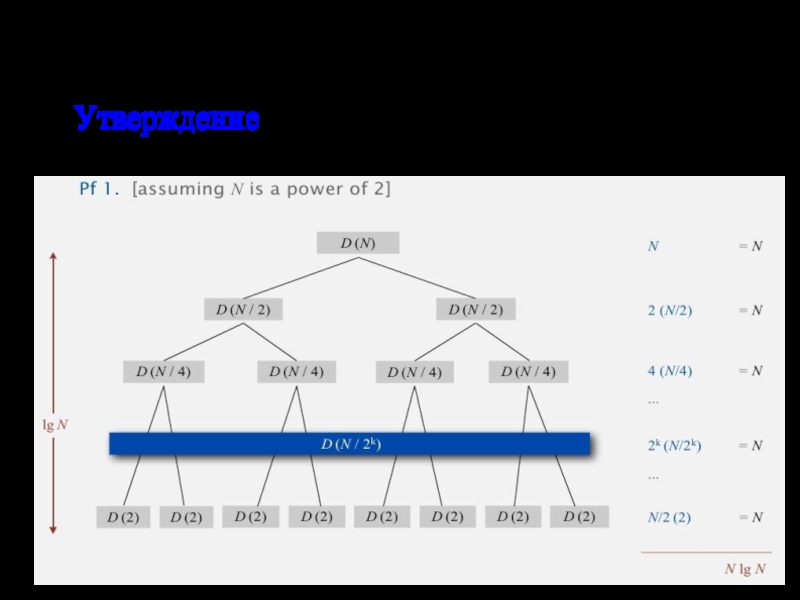
Слайд 16Разделяй и властвуй
Утверждение. Если D(N) удовлетворяет D(N) = 2D(N/2) + N,
Слайд 17Разделяй и властвуй
Утверждение. Если D(N) удовлетворяет D(N) = 2D(N/2) + N,
Слайд 18Разделяй и властвуй
Утверждение. Если D(N) удовлетворяет D(N) = 2 D(N/2) +
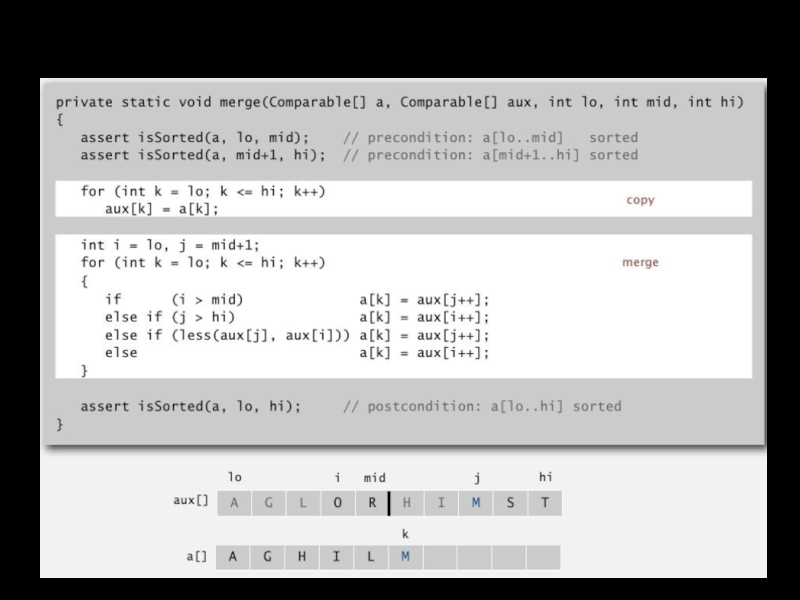
Слайд 19Анализ сортировки слиянием: память
Утверждение. Сортировка слиянием использует дополнительную память пропорциональную N
Массиву
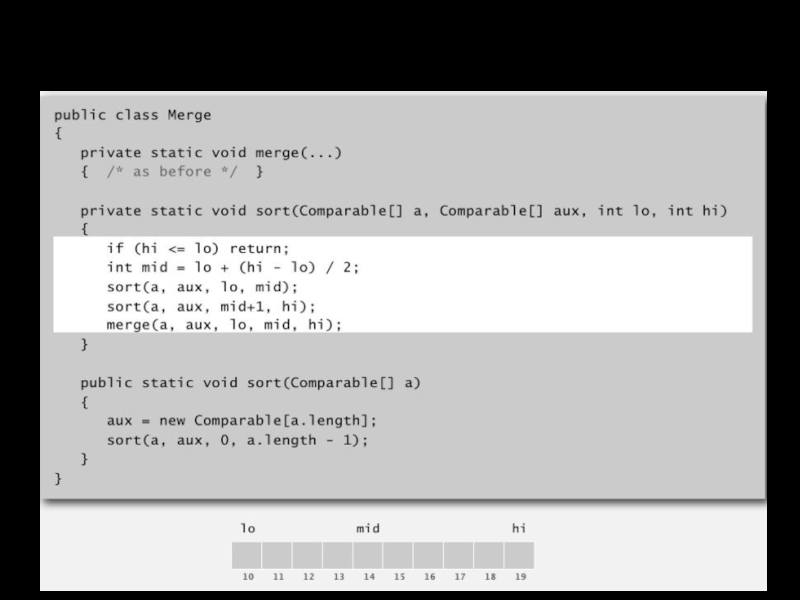
Слайд 20Сортировка слиянием: реализация
Используйте сортировку вставками для маленьких подмассивов
Сортировка слиянием очень дорогая
Подмассивы для сортировки вставками ~ 7
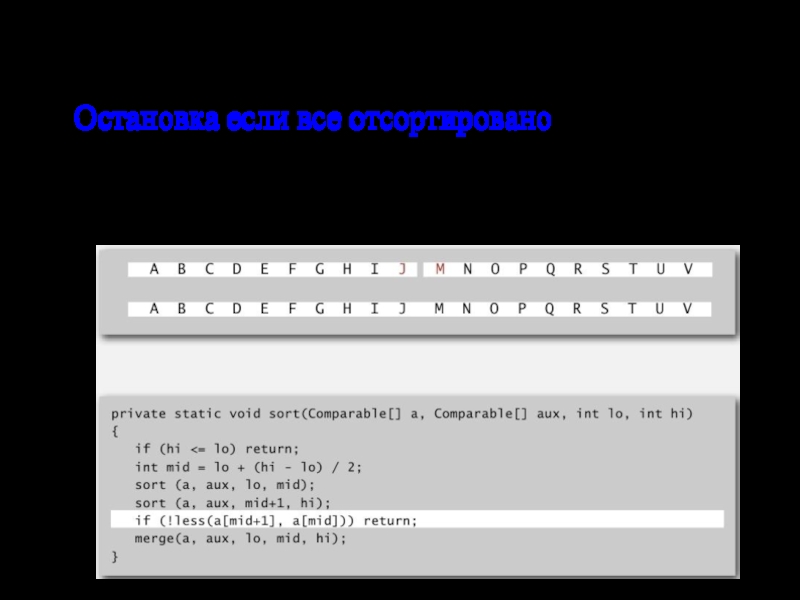
Слайд 21Сортировка слиянием: реализация
Остановка если все отсортировано
Если самый большой элемент первой половины
Полезно для частично-упорядоченного массива
Слайд 22Сортировка слиянием: реализация
Ограничить копирование во вспомогательный массив
Экономит время (но не память).
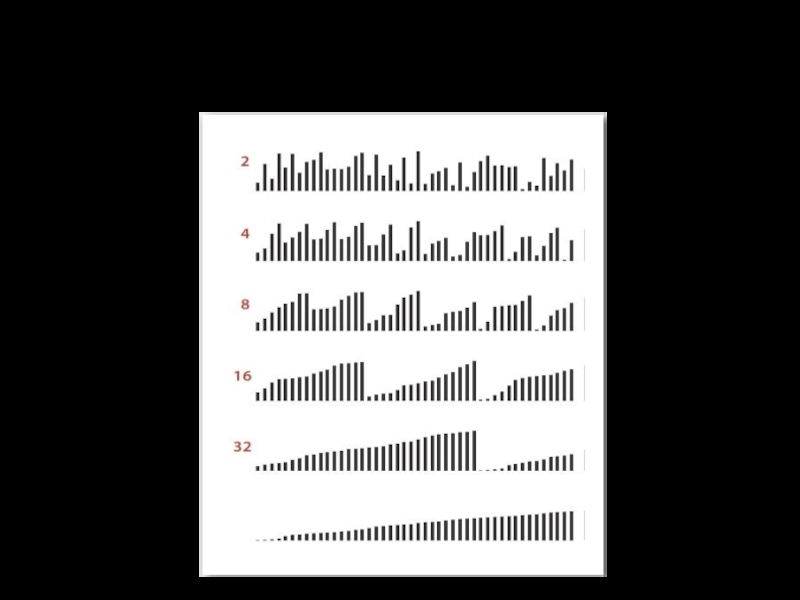
Слайд 25Восходящая сортировка слиянием
Начинаем со слияния подмассивов с размером 1
Повторяем для подмассивов
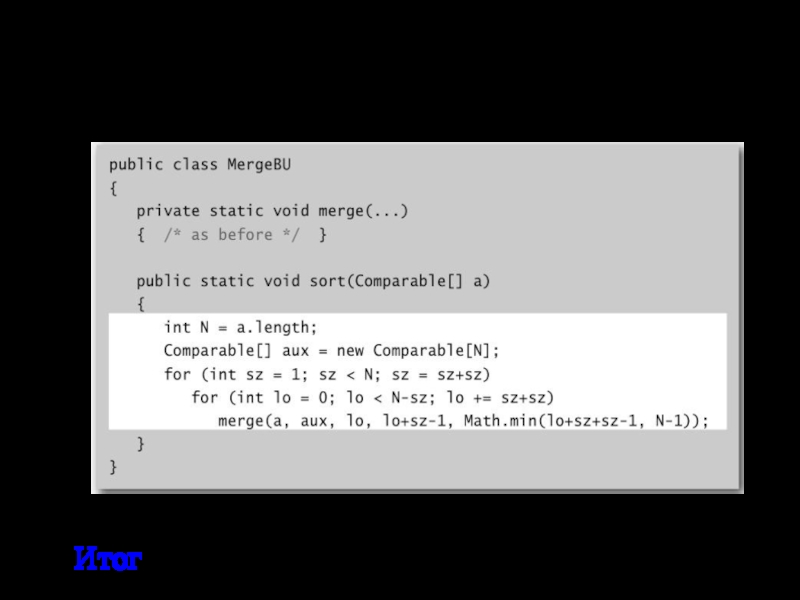
Слайд 26Восходящая сортировка слиянием: реализация на Java
Итог. Простая и не рекурсивная версия
Слайд 29Сложность сортировки
Вычислительная сложность - основа для обучения эффективным алгоритмам для решения
Вычислительная модель. Возможные операции
Стоимость модели. Количество операций
Верхняя граница. Стоимость, гарантированная определенным алгоритмам для задачи Х
Нижняя граница. Доказанное ограничение стоимости для всех алгоритмов для задачи Х
Оптимальный алгоритм. Алгоритм с лучшей максимально возможной стоимостью для задачи Х (когда верхняя и нижняя граница приблизительно совпадают)
Пример: сортировка
Вычислительная модель: дерево принятия решений
Стоимость модели: количество сравнений
Верхняя граница: ~ Nlog2N для сортировки слиянием
Нижняя граница: ?
Оптимальный алгоритм: ?
Слайд 31Нижняя граница для сортировки на основе сравнений
Утверждение. Ни один алгоритм сортировки,
Доказательство
Все элементы массива различны
В худшем случае высота дерева будет h
Бинарное дерево высотой h имеет максимум 2h листьев
N! <= количество листьев <= 2h
Слайд 32Нижняя граница для сортировки на основе сравнений
Утверждение. Ни один алгоритм сортировки,
Доказательство
Все элементы массива различны
В худшем случае высота дерева будет h
Бинарное дерево высотой h имеет максимум 2h листьев
N! <= количество листьев <= 2h
Слайд 33Сложность сортировки
Вычислительная модель. Возможные операции
Стоимость модели. Количество операций
Верхняя граница. Стоимость, гарантированная
Нижняя граница. Доказанное ограничение стоимости для всех алгоритмов для задачи Х
Оптимальный алгоритм. Алгоритм с лучшей максимально возможной стоимостью для задачи Х (когда верхняя и нижняя граница приблизительно совпадают)
Пример: сортировка
Вычислительная модель: дерево принятия решений
Стоимость модели: количество сравнений
Верхняя граница: ~ Nlog2N для сортировки слиянием
Нижняя граница: ~ Nlog2N
Оптимальный алгоритм: сортировка слиянием
Первая цель разработки алгоритмов: оптимальный алгоритм
Слайд 34Сложность сортировки
Сравнения? Сортировка слиянием оптимальна по количеству сравнений
Память? Сортировка слиянием не
Урок. Руководствуйся теорией
Не пытайтесь создать алгоритм сортировки гарантирующий ½ Nlog2N сравнений
Слайд 35Сложность сортировки
Можно снизить нижнюю границу для сортировки если есть информация о:
Упорядоченности
Распределении значений ключей
Представлении ключей
Частично-упорядоченный массив
Дубликаты ключей. Зная распределение дубликатов во входных данных, мы можем отказаться от NlogN
Представление ключей. Можем использовать цифровые/символьные сравнения ключей вместо сравнений номеров и строк
Слайд 37Устойчивость
Типичная задача. Отсортировать сначала по имени, а затем, по группам
Студенты из
Устойчивые сортировки сохраняют порядок элементов с одинаковыми ключами







![Сортировка слияниемЦель. Получить два отсортированных подмассива от a[lo] до a[mid] и от a[mid+1] до a[hi]Видео 1](/img/tmb/1/9678/4e428cecfdf22c0b06fd897fe362b0d6-800x.jpg)






![Анализ сортировки слиянием: памятьУтверждение. Сортировка слиянием использует дополнительную память пропорциональную NМассиву aux[] нужен N ячеек](/img/tmb/1/9678/3318a181542ac223fcfcac37696ee6e7-800x.jpg)