- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поиск решения задачи коммивояжера на взвешенных ориентированных сильносвязных графах методами типа ветвей и границ презентация
Содержание
- 1. Поиск решения задачи коммивояжера на взвешенных ориентированных сильносвязных графах методами типа ветвей и границ
- 2. СОДЕРЖАНИЕ 1. Постановки задач коммивояжера. 2. Решение
- 3. Часть 1 Постановки задач коммивояжера
- 4. Содержательные постановки «классических» задач коммивояжера 1. Разомкнутая
- 5. Графовая интерпретация замкнутой задачи коммивояжера
- 6. Обозначения и определения
- 7. Формальная постановка аддитивной замкнутой задачи коммивояжера
- 8. Формальная постановка аддитивной разомкнутой задачи коммивояжера
- 9. Формальная постановка минимаксной разомкнутой задачи коммивояжера Самостоятельно: дать формальную постановку минимаксной замкнутой задачи коммивояжера.
- 10. Переменные для формальной постановки разомкнутой задачи коммивояжера
- 11. формальные постановки задач коммивояжера как функции от
- 12. Часть 2. Методы типа
- 13. ПРОСТОЙ СПОСОБ ВЫЧИСЛЕНИЯ ОЦЕНКИ Оценкой является суммарный
- 14. Простой способ вычисления оценки и фронтальный спуск
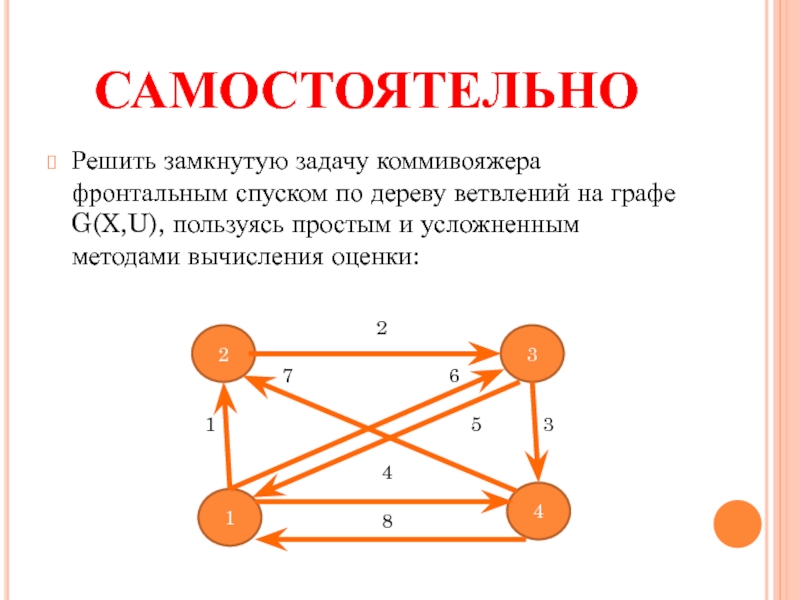
- 15. Решить замкнутую задачу коммивояжера самостоятельно, пользуясь МВГ, реализующим фронтальный спуск по дереву ветвлений
- 16. УТОЧНЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ОЦЕНКИ Оценкой является сумма,
- 17. ПРИМЕР ВЫЧИСЛЕНИЯ УТОЧНЕННОЙ ОЦЕНКИ Пусть I =
- 18. Уточненный способ вычисления оценки и фронтальный спуск
- 19. САМОСТОЯТЕЛЬНО Решить замкнутую задачу коммивояжера фронтальным спуском
- 20. Простой способ вычисления оценки и поиск с
- 21. Уточненный способ вычисления оценки и поиск с
- 22. САМОСТОЯТЕЛЬНО Определить решение замкнутой задачи коммивояжера, осуществляя
- 23. ЧАСТЬ 3 РЕШЕНИЕ РАЗОМКНУТОЙ ЗАДАЧИ КОММИВОЯЖЕРА МЕТОДАМИ ТИПА ВЕТВЕЙ И ГРАНИЦ
- 24. АЛГОРИТМ ПЕРЕХОДА ОТ РАЗОМКНУТОЙ «КЛАССИЧЕСКОЙ» ЗАДАЧИ КОММИВОЯЖЕРА
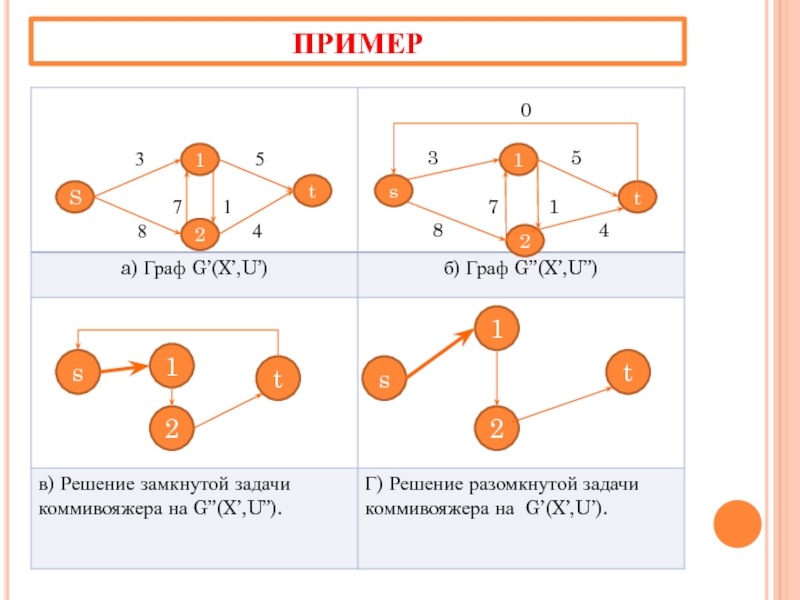
- 25. ПРИМЕР S 2 1 t s 1
- 26. Эквивалентные преобразования графа, на котором решается разомкнутая
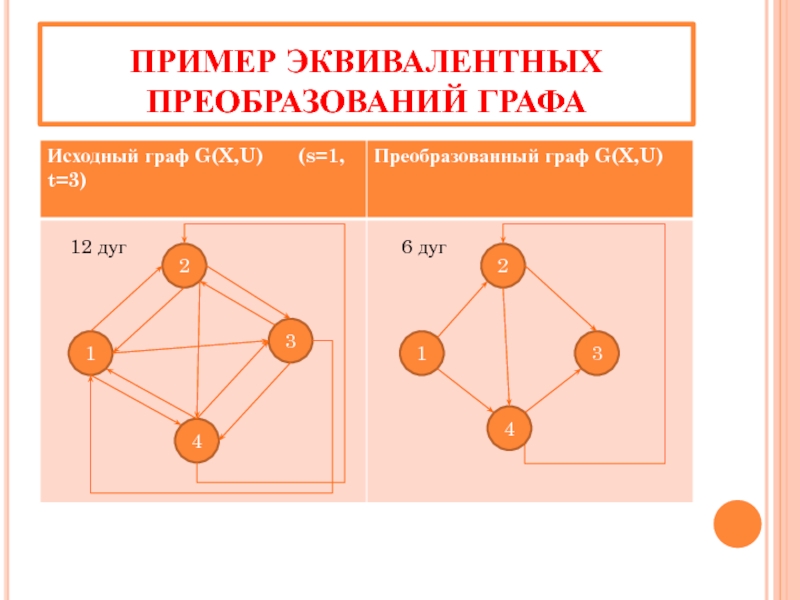
- 27. ПРИМЕР ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ ГРАФА 1 3 4
- 28. САМОСТОЯТЕЛЬНО Определить решение методом типа ветвей и
- 29. САМОСТОЯТЕЛЬНО Предложите свой способ решения
Слайд 1Лекция 14
Поиск решения задачи коммивояжера на взвешенных ориентированных сильносвязных графах методами
Слайд 2СОДЕРЖАНИЕ
1. Постановки задач коммивояжера.
2. Решение замкнутой задачи коммивояжера методами типа ветвей
3. Решение разомкнутой задачи коммивояжера методами типа ветвей и границ.
Слайд 4Содержательные постановки «классических» задач коммивояжера
1. Разомкнутая постановка задачи: коммивояжер должен объехать
- минимум средств на максимальный переход.
2. Замкнутая постановка задачи: коммивояжер должен объехать все n городов, побывав в каждом по одному разу и вернуться в город из которого стартовал, затратив: -минимум средств на путешествие (аддитивная задача коммивояжера)
- минимум средств на максимальный переход (минимаксная задача коммивояжера).
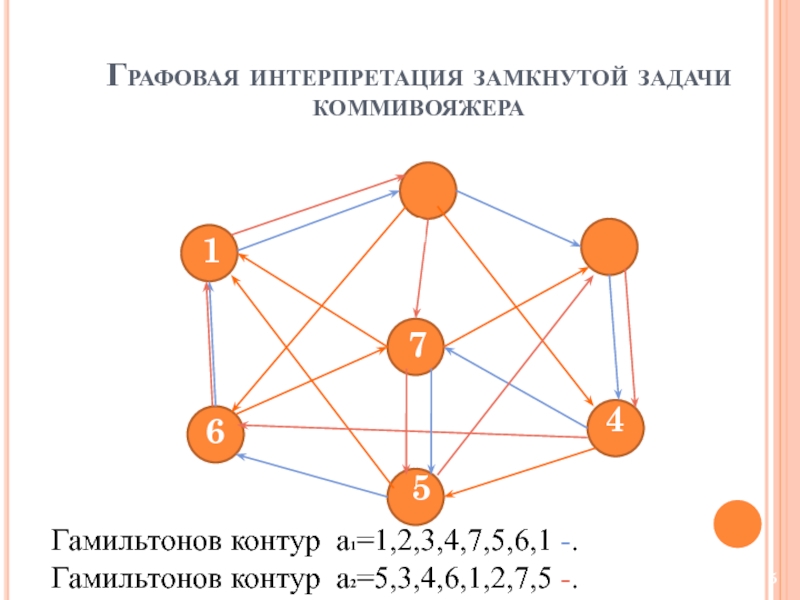
Слайд 5Графовая интерпретация замкнутой задачи коммивояжера
1
2
7
4
3
5
6
Гамильтонов контур
Гамильтонов контур а2=5,3,4,6,1,2,7,5 -.
Слайд 9Формальная постановка минимаксной разомкнутой задачи коммивояжера
Самостоятельно: дать формальную постановку минимаксной замкнутой
Слайд 10Переменные для формальной постановки разомкнутой задачи коммивояжера как функции от перестановки
Пусть
Пусть переменная y(ij,i(j+1)) определена следующим образом:
r(ij,i(j+1)), если дуга (ij. i(j+1)) принадлежит
множеству U;
y(ij,i(j+1)) =
∞ в противном случае.
Слайд 11формальные постановки задач коммивояжера как функции от перестановки
Формальная постановка разомкнутой задачи
Формальная постановка замкнутой задачи коммивояжера:
Слайд 12Часть 2.
Методы типа ветвей и границ, осуществляющие поиск
Слайд 13ПРОСТОЙ СПОСОБ ВЫЧИСЛЕНИЯ ОЦЕНКИ
Оценкой является суммарный вес удаленных дуг.
Пусть I –
Тогда оценка Δ равна:
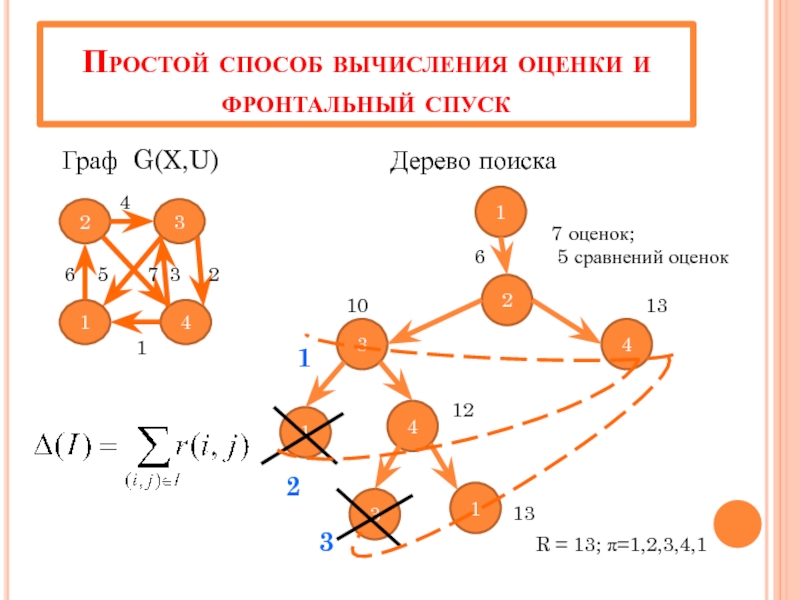
Слайд 14Простой способ вычисления оценки и фронтальный спуск
Граф G(X,U)
2
4
1
3
4
6 5 7 3 2
1
1
2
4
3
4
1
1
3
7 оценок;
6 5 сравнений оценок
10 13
1
12
2
13
3 R = 13; π=1,2,3,4,1
Слайд 15Решить замкнутую задачу коммивояжера самостоятельно, пользуясь МВГ, реализующим фронтальный спуск по
Слайд 16УТОЧНЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ОЦЕНКИ
Оценкой является сумма, включающая суммарный вес удаленных дуг
Пусть I – подмножество удаленных дуг, а J – подмножество вершин, соответствующих городам, в которые коммивояжер еще не въезжал.
Тогда оценка Δ равна:
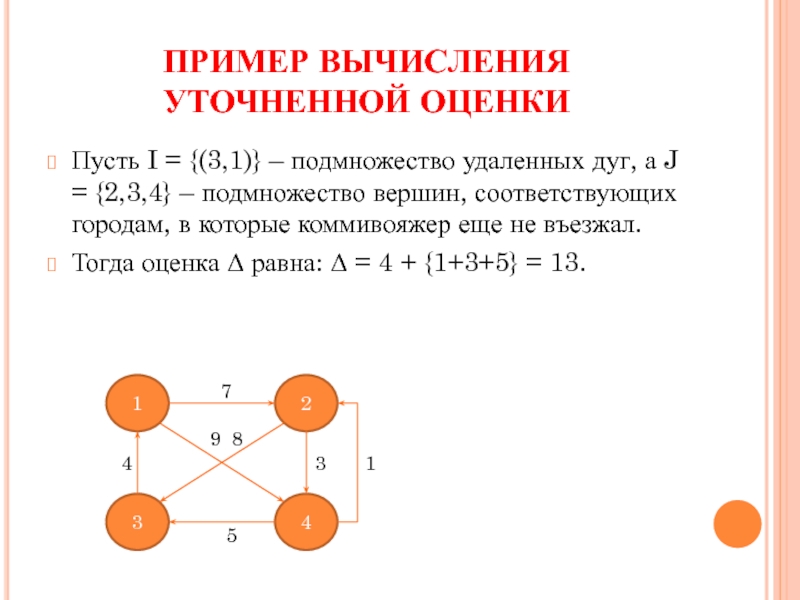
Слайд 17ПРИМЕР ВЫЧИСЛЕНИЯ УТОЧНЕННОЙ ОЦЕНКИ
Пусть I = {(3,1)} – подмножество удаленных дуг,
Тогда оценка Δ равна: Δ = 4 + {1+3+5} = 13.
1
3
4
2
7
9 8
4 3 1
5
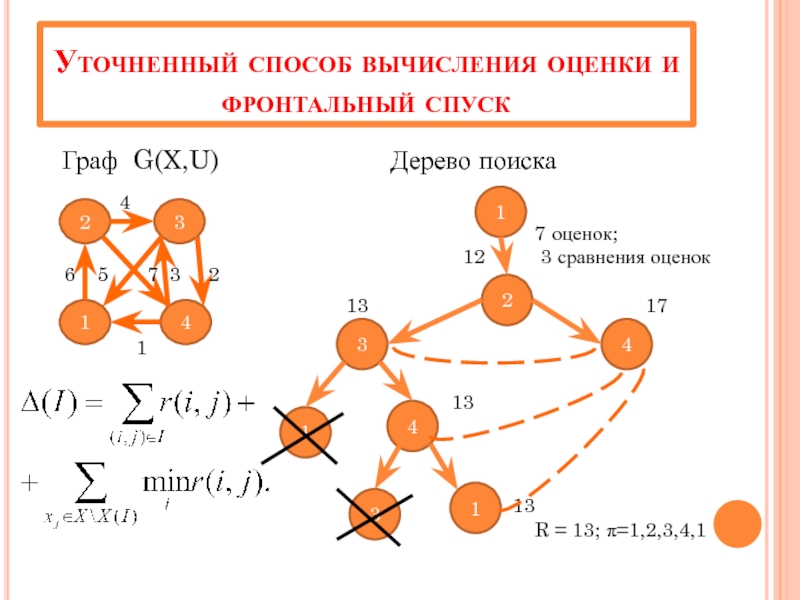
Слайд 18Уточненный способ вычисления оценки и фронтальный спуск
Граф G(X,U)
2
4
1
3
4
6 5 7 3 2
1
1
2
4
3
4
1
1
3
7 оценок;
12 3 сравнения оценок
13 17
13
13
R = 13; π=1,2,3,4,1
Слайд 19САМОСТОЯТЕЛЬНО
Решить замкнутую задачу коммивояжера фронтальным спуском по дереву ветвлений на графе
2
1
4
3
2
7 6
1 5 3
4
8
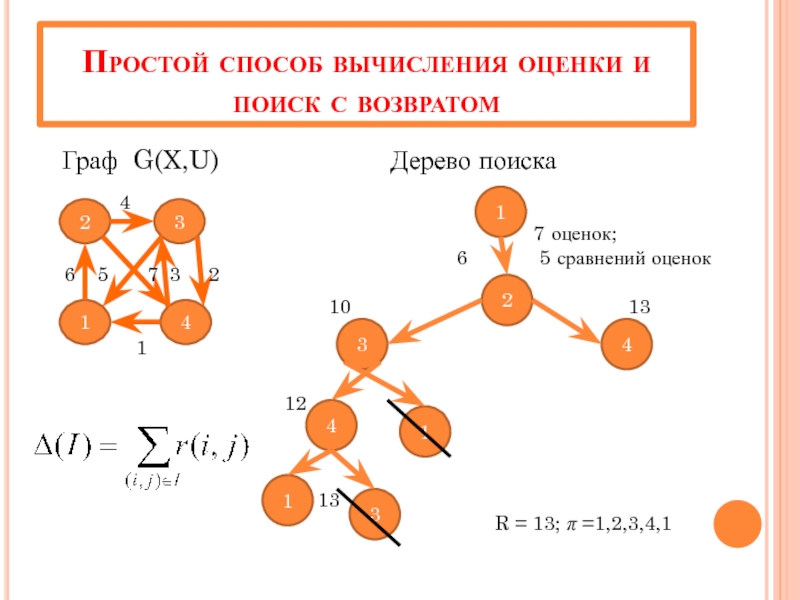
Слайд 20Простой способ вычисления оценки и поиск с возвратом
Граф G(X,U)
2
4
1
3
4
6 5 7 3 2
1
1
2
4
3
4
1
1
3
7 оценок;
6 5 сравнений оценок
10 13
12
13
R = 13; π =1,2,3,4,1
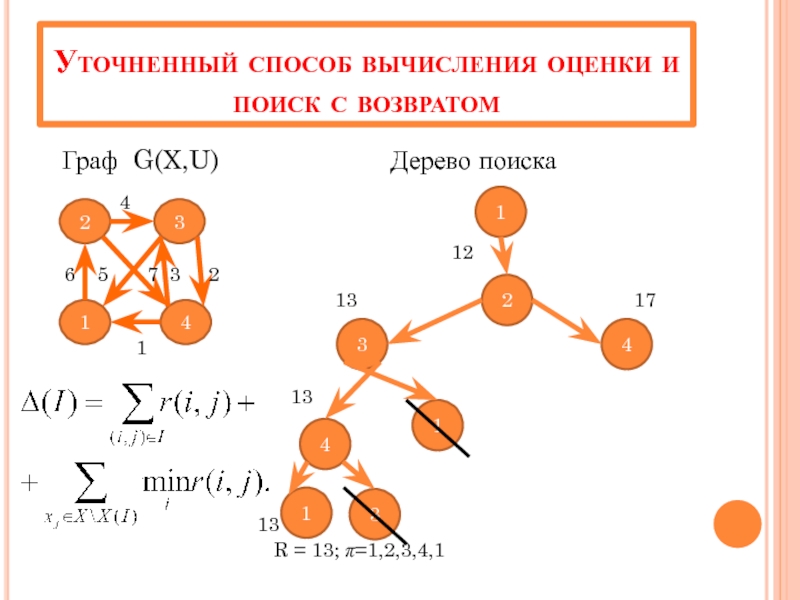
Слайд 21Уточненный способ вычисления оценки и поиск с возвратом
Граф G(X,U)
2
4
1
3
4
6 5 7 3 2
1
1
2
4
3
4
1
1
3
12
13 17
13
13
R = 13; π=1,2,3,4,1
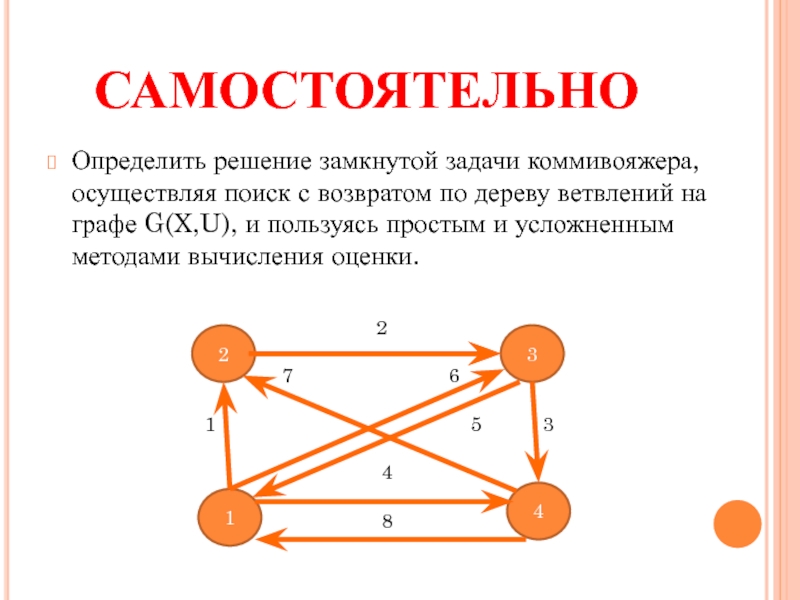
Слайд 22САМОСТОЯТЕЛЬНО
Определить решение замкнутой задачи коммивояжера, осуществляя поиск с возвратом по дереву
2
1
4
3
2
7 6
1 5 3
4
8
Слайд 24АЛГОРИТМ ПЕРЕХОДА ОТ РАЗОМКНУТОЙ «КЛАССИЧЕСКОЙ» ЗАДАЧИ КОММИВОЯЖЕРА К ЗАМКНУТОЙ
Пусть задан орграф
Преобразуем G’(X’,U,) в орграф G”(X’,U”) добавлением дуги (t,s), обладающей нулевым весом.
На орграфе G”(X’,U”) ищется оптимальное решение замкнутой задачи коммивояжера.
Отбрасывая в полученном на предыдущем шаге подмножестве дуг, дугу (t,s), получим решение разомкнутой задачи коммивояжера.
Слайд 26Эквивалентные преобразования графа, на котором решается разомкнутая задача коммивояжера
1. Если на
Если на исходном графе существуют дуги, ведущие в стартовую вершину, то они могут быть отброшены.
Если на исходном графе существуют дуги, ведущие из терминальной вершины, то они могут быть отброшены.
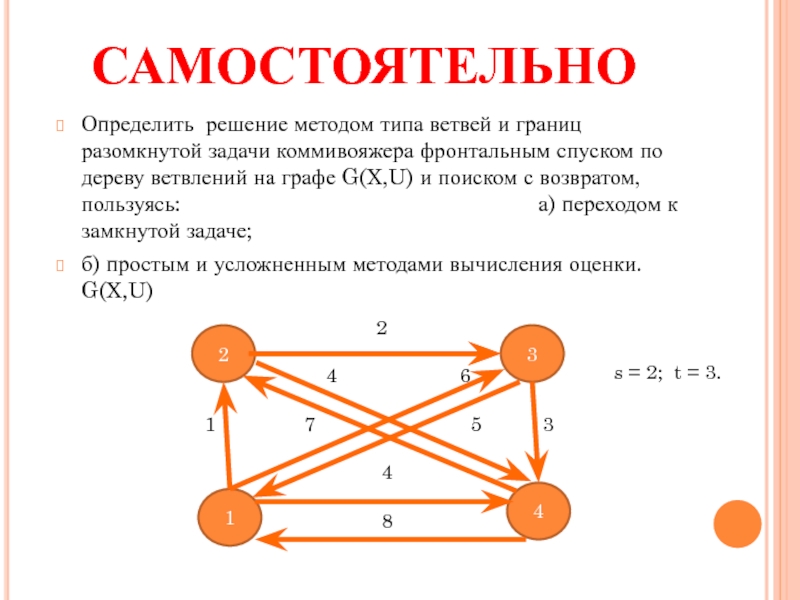
Слайд 28САМОСТОЯТЕЛЬНО
Определить решение методом типа ветвей и границ разомкнутой задачи коммивояжера фронтальным
б) простым и усложненным методами вычисления оценки. G(X,U)
2
1
4
3
2
4 6
1 7 5 3
4
8
s = 2; t = 3.