- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графи та їх різновиди презентация
Содержание
- 1. Графи та їх різновиди
- 2. План Основи теорії графів Види графів
- 3. Теорія графів — розділ математики, що
- 4. 1)Якщо ребро з'єднує дві вершини, то кажуть,
- 5. 3)Вершини, які не належать кінцям жодного з
- 6. Види графів: НУЛЬ - ГРАФ ПОРОЖНІЙ
- 7. НУЛЬ-ГРАФ Граф, який складається лише з ізольованих
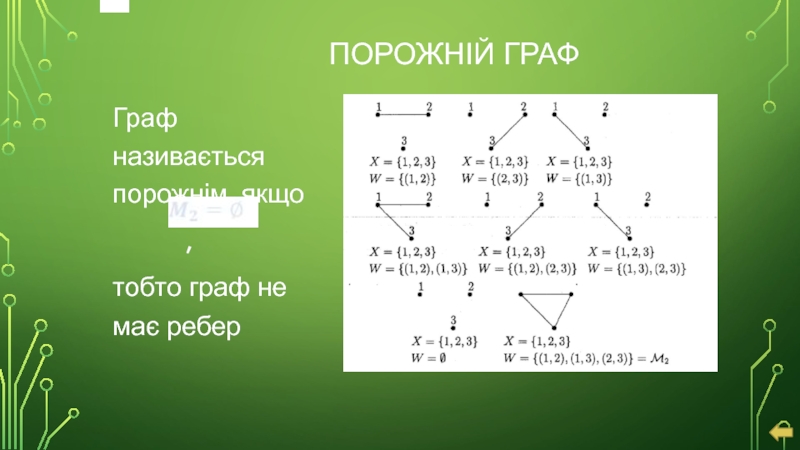
- 8. ПОРОЖНІЙ ГРАФ Граф називається порожнім, якщо
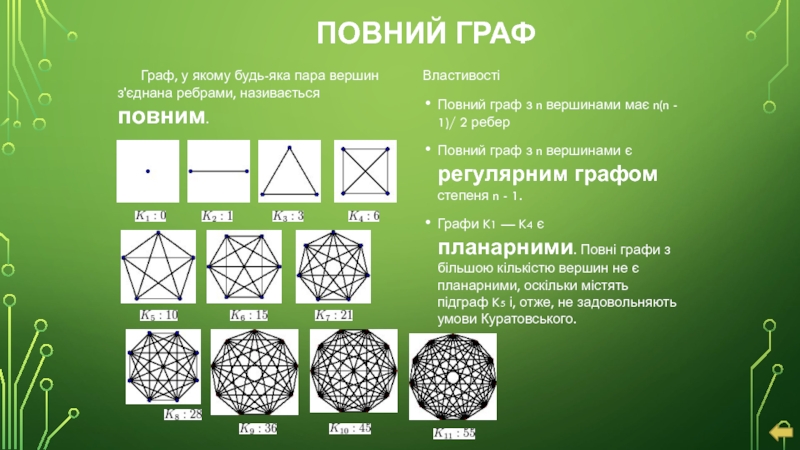
- 9. ПОВНИЙ ГРАФ Граф, у якому будь-яка пара
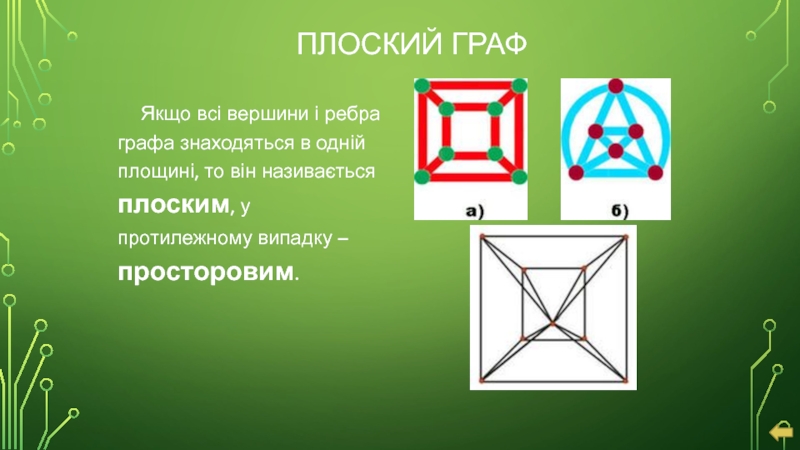
- 10. ПЛОСКИЙ ГРАФ Якщо всі вершини і ребра
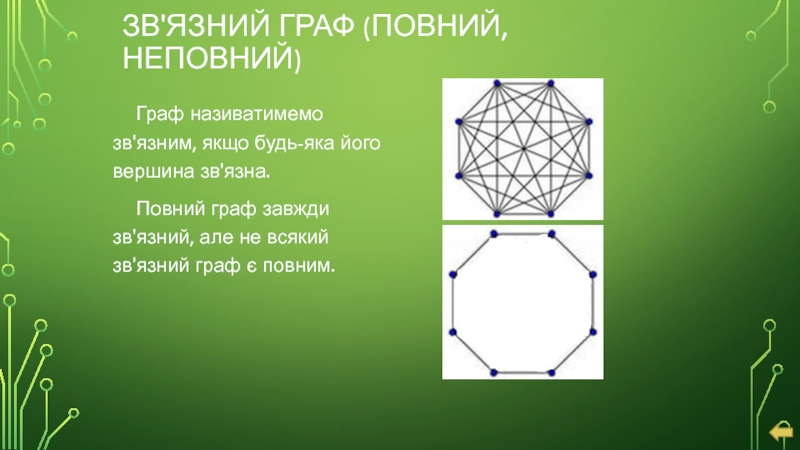
- 11. ЗВ'ЯЗНИЙ ГРАФ (ПОВНИЙ, НЕПОВНИЙ) Граф називатимемо зв'язним,
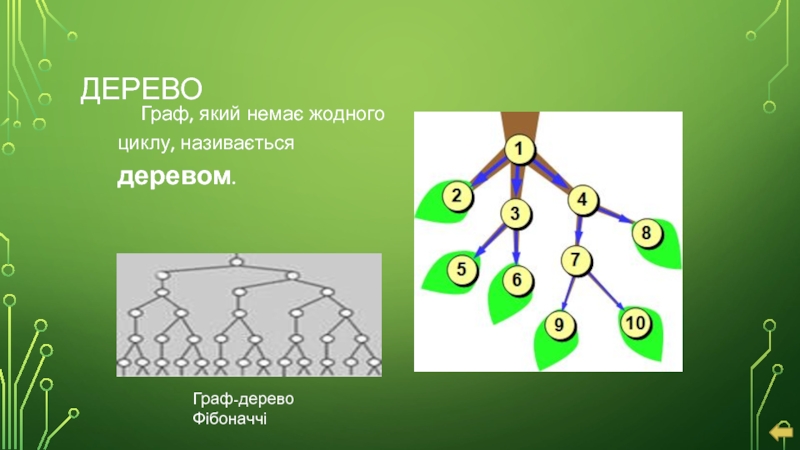
- 12. ДЕРЕВО Граф, який немає жодного циклу, називається деревом. Граф-дерево Фібоначчі
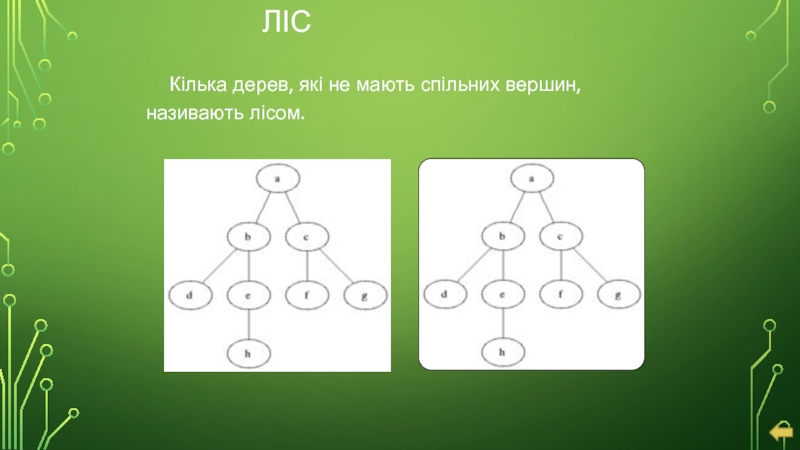
- 13. Кілька дерев, які не мають спільних вершин, називають лісом. ЛІС
- 14. ОРІЄНТОВАНИЙ ГРАФ Граф, у якому для всіх
- 15. НЕОГРАФ Неорієнтований граф (неограф) — це
- 16. ОРГРАФ Орієнтований граф (орграф) — це
- 17. ЗВАЖЕНИЙ ГРАФ Якщо у графі вказана “вага”
- 18. ЗМІШАНИЙ ГРАФ Змішаний граф – це граф,
- 19. ГРАФ ЯК ГЕОМЕТРИЧНА КОНФІГУРАЦІЯ Наочно граф можна
- 20. ЕЙЛЕРІВ ГРАФ Граф називається ейлеровим, якщо в
- 21. Ойлер зауважив, що його граф не являє
- 22. ЗВ'ЯЗНИЙ ГРАФ ЗА ОЙЛЕРОМ Зв’язний граф називається
Слайд 3
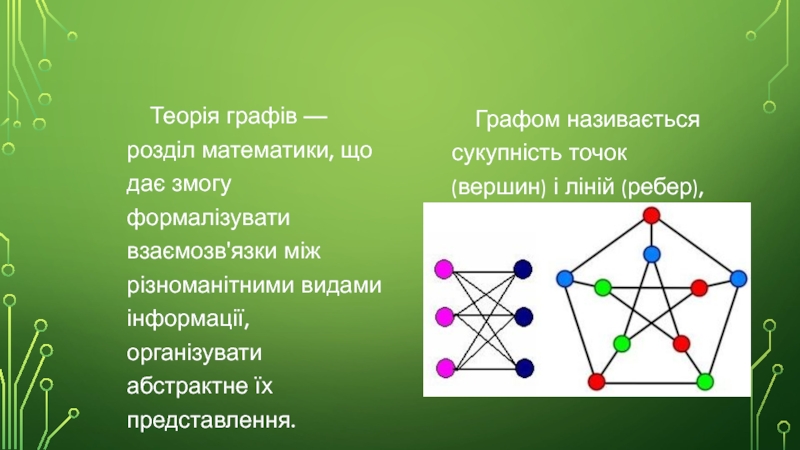
Теорія графів — розділ математики, що дає змогу формалізувати взаємозв'язки між
Графом називається сукупність точок (вершин) і ліній (ребер), що їх з'єднують.
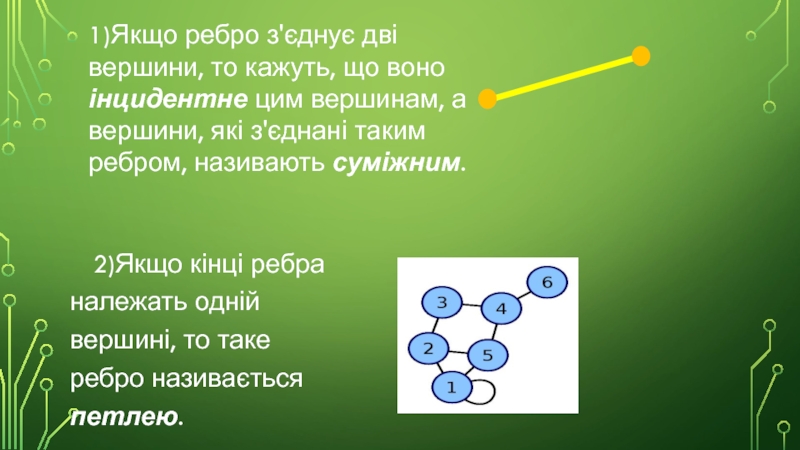
Слайд 41)Якщо ребро з'єднує дві вершини, то кажуть, що воно інцидентне цим
2)Якщо кінці ребра належать одній вершині, то таке ребро називається петлею.
Слайд 53)Вершини, які не належать кінцям жодного з ребер у графі, називаються
Вершина А – приклад ізольованої вершини.
А
Слайд 6Види графів:
НУЛЬ - ГРАФ
ПОРОЖНІЙ ГРАФ
ПОВНИЙ ГРАФ
ЗВ’ЯЗНИЙ ГРАФ
ДЕРЕВО
ПЛОСКИЙ
ЛІС
ОРІЄНТОВАНИЙ ГРАФ
НЕОГРАФ
ОРГРАФ
ЗВАЖЕНИЙ ГРАФ
ЗМІШАНИЙ ГРАФ
ГРАФ,ЯК КОНФІГУРАЦІЯ
ЕЙЛЕРІВ ГРАФ
ЗВ’ЯЗНИЙ ГРАФ ЗА ОЙЛЕРОМ
Слайд 7НУЛЬ-ГРАФ
Граф, який складається лише з ізольованих вершин, називається нуль-графом.
В графі ребро
Слайд 9ПОВНИЙ ГРАФ
Граф, у якому будь-яка пара вершин з'єднана ребрами, називається повним.
Властивості
Повний
Повний граф з n вершинами є регулярним графом степеня n - 1.
Графи K1 — K4 є планарними. Повні графи з більшою кількістю вершин не є планарними, оскільки містять підграф K5 і, отже, не задовольняють умови Куратовського.
Слайд 10ПЛОСКИЙ ГРАФ
Якщо всі вершини і ребра графа знаходяться в одній площині,
Слайд 11ЗВ'ЯЗНИЙ ГРАФ (ПОВНИЙ, НЕПОВНИЙ)
Граф називатимемо зв'язним, якщо будь-яка його вершина зв'язна.
Повний граф завжди зв'язний, але не всякий зв'язний граф є повним.
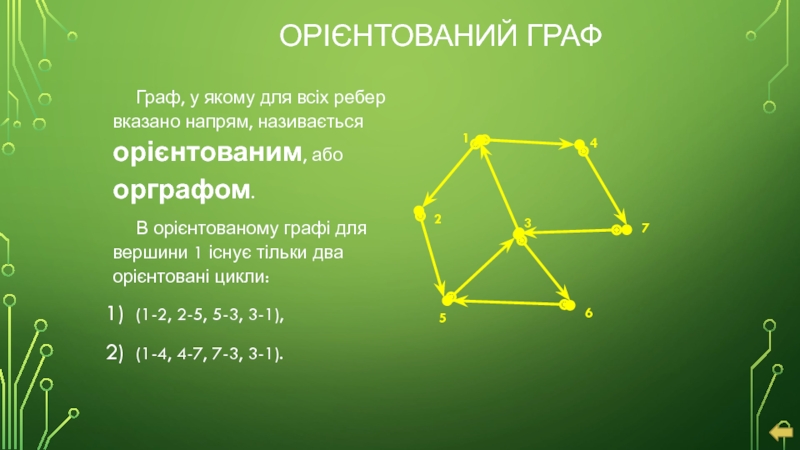
Слайд 14ОРІЄНТОВАНИЙ ГРАФ
Граф, у якому для всіх ребер вказано напрям, називається орієнтованим,
В орієнтованому графі для вершини 1 існує тільки два орієнтовані цикли:
(1-2, 2-5, 5-3, 3-1),
(1-4, 4-7, 7-3, 3-1).
1
2
3
4
5
6
7
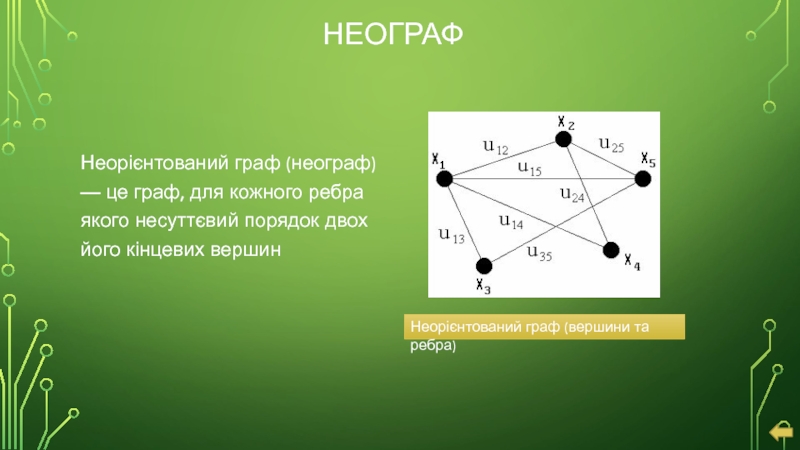
Слайд 15НЕОГРАФ
Неорієнтований граф (неограф) — це граф, для кожного ребра якого
Неорієнтований граф (вершини та ребра)
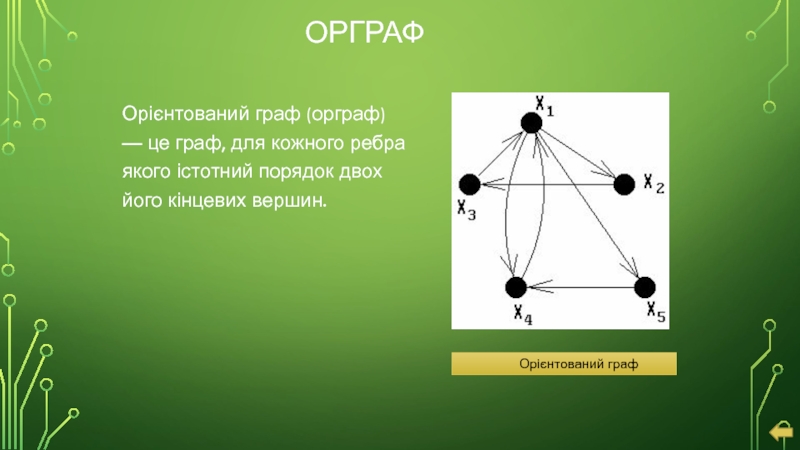
Слайд 16ОРГРАФ
Орієнтований граф (орграф) — це граф, для кожного ребра якого
Орієнтований граф
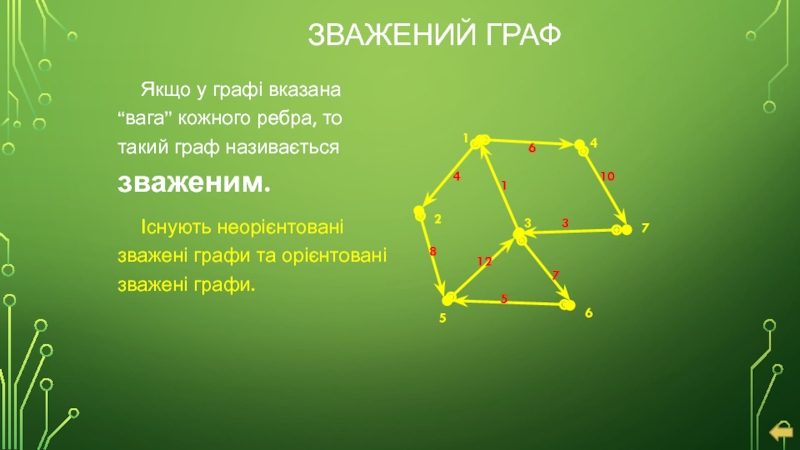
Слайд 17ЗВАЖЕНИЙ ГРАФ
Якщо у графі вказана “вага” кожного ребра, то такий граф
Існують неорієнтовані зважені графи та орієнтовані зважені графи.
1
2
3
4
5
6
7
4
6
10
3
1
12
8
7
5
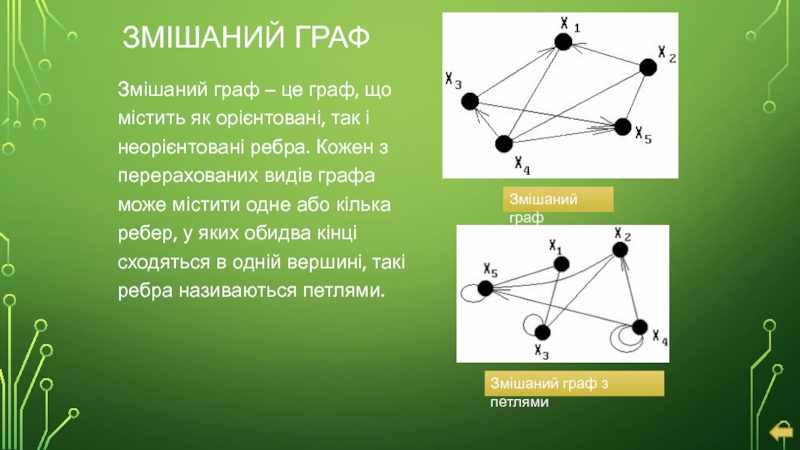
Слайд 18ЗМІШАНИЙ ГРАФ
Змішаний граф – це граф, що містить як орієнтовані, так
Змішаний граф
Змішаний граф з петлями
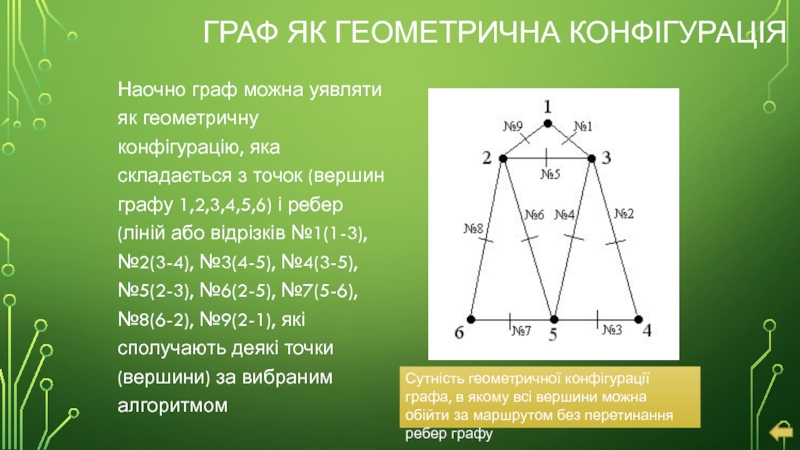
Слайд 19ГРАФ ЯК ГЕОМЕТРИЧНА КОНФІГУРАЦІЯ
Наочно граф можна уявляти як геометричну конфігурацію, яка
Сутність геометричної конфігурації графа, в якому всі вершини можна обійти за маршрутом без перетинання ребер графу
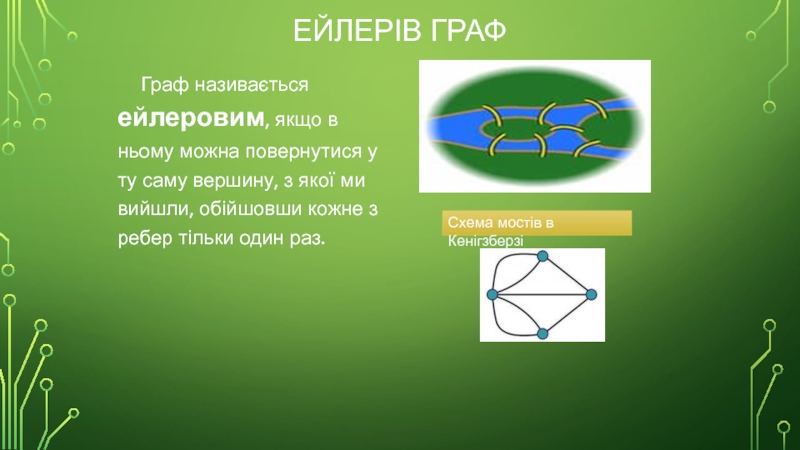
Слайд 20ЕЙЛЕРІВ ГРАФ
Граф називається ейлеровим, якщо в ньому можна повернутися у ту
Схема мостів в Кенігзберзі
Слайд 21Ойлер зауважив, що його граф не являє єдиного циклу: з якої
Виклавши розв'язання задачі про кенігсберзькі мости, Ойлер в своїй праці поставив питання: на яких графах можна знайти цикл, який містить всі ребра графа, при чому кожне ребро зустрічається в циклі рівно один раз?
Це дало початок системному математичному підходу до побудови та вивчення властивості графів.
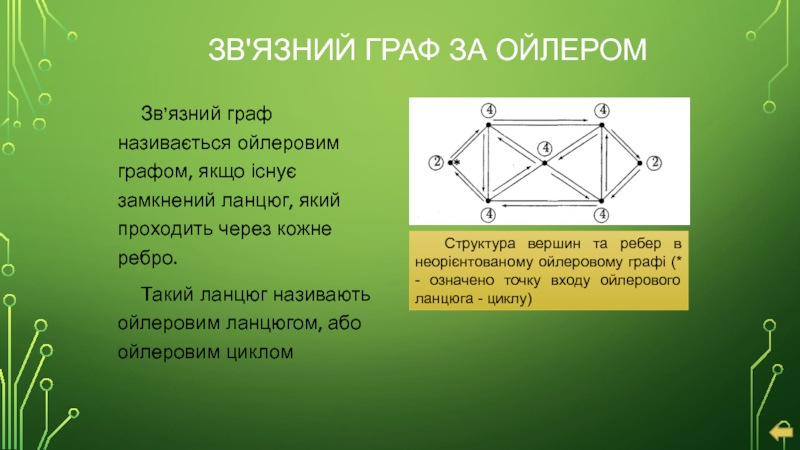
Слайд 22ЗВ'ЯЗНИЙ ГРАФ ЗА ОЙЛЕРОМ
Зв’язний граф називається ойлеровим графом, якщо існує замкнений
Такий ланцюг називають ойлеровим ланцюгом, або ойлеровим циклом
Структура вершин та ребер в неорієнтованому ойлеровому графі (* - означено точку входу ойлерового ланцюга - циклу)