- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проверка аутентичности цифровых изображений формата JPEG презентация
Содержание
- 1. Проверка аутентичности цифровых изображений формата JPEG
- 4. При визуальном анализе оцениваются: - естественность
- 7. Анализ информации о файле: - стандартные
- 8. Шаг 1. Переводим изображение из пространства RGB
- 9. При больших степенях сжатия блок 8х8 раскладывается
- 10. Шаг 3. Применение ДКП к блокам изображения 8х8
- 11. Преобразование блока изображения f(x,y) в блок ДКП коэффициентовF(m,n):
- 12. Шаг 4. Квантование. На этом шаге происходит отбрасывание
- 13. Шаг 6. Преобразовываем вектор с помощью модифицированного алгоритма
- 14. 158 128 121 117 136 128 128
- 15. Сжали 64 байта в 22!
- 16. Рис. 1. Элементы матрицы квантования в графических
- 18. Анализ ошибки сжатия Двойной эффект квантования (Double
- 19. Анализ ошибки сжатия
- 20. Double Quantization effect FQ(m, n) =
- 22. Определения фотомонтажа путем анализа следов матрицы камеры
- 24. Анализ пиксельных связей
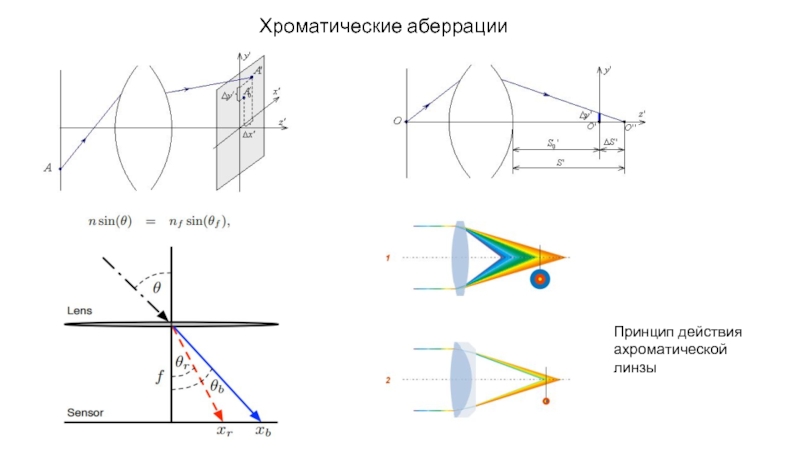
- 25. Принцип действия ахроматической линзы Хроматические аберрации
- 27. Результаты работы алгоритма для оригинального и модифицированного изображений
- 28. Функции отклика камеры для двух разных областей изображения
- 29. Шум на фотографии
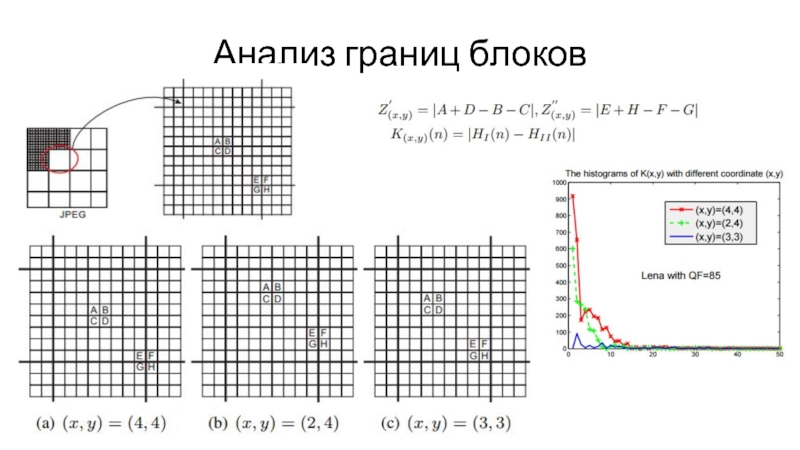
- 32. Анализ границ блоков
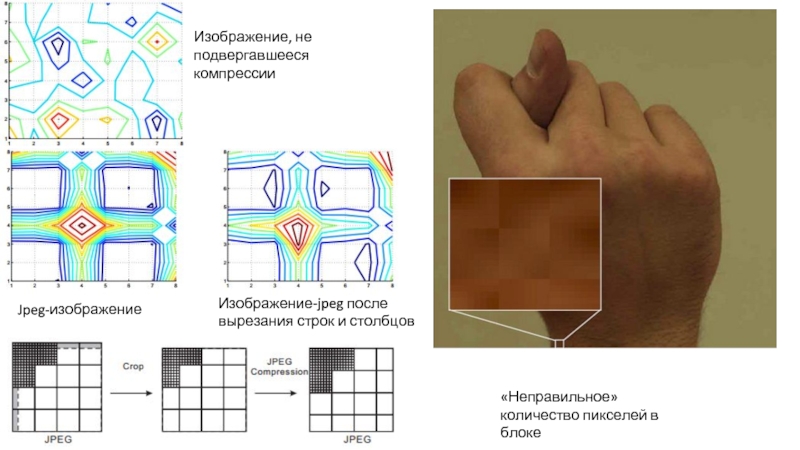
- 33. Изображение, не подвергавшееся компрессии Jpeg-изображение Изображение-jpeg после
- 34. Статистические атаки на основе критерия хи-квадрат.
Слайд 4При визуальном анализе оцениваются:
- естественность композиции изображения;
- пропорциональность частей
- перспективное соответствие и одинаковый ракурс всех деталей изображения;
- одинаковые условия освещения объектов;
- распределение теней и световых бликов;
- уровни яркости и цветовой баланс всех частей изображения;
- одинаковая степень резкости и «зернистости»;
- однородность фона, плавность перехода между соседними фрагментами.
Слайд 7Анализ информации о файле:
- стандартные пропорции фотографии
- информация EXIF, миниатюрный эскиз
- элементы матрицы квантования;
- длина таблицы Хаффмана;
Слайд 8Шаг 1. Переводим изображение из пространства RGB в пространство YCbCr с
Шаг 2. Разбиваем исходное изображение на матрицы 8х8
Слайд 9При больших степенях сжатия блок 8х8 раскладывается на компоненты YCbCr в
Формируем из каждой три рабочие матрицы ДКП – по 8 бит отдельно для каждой компоненты.
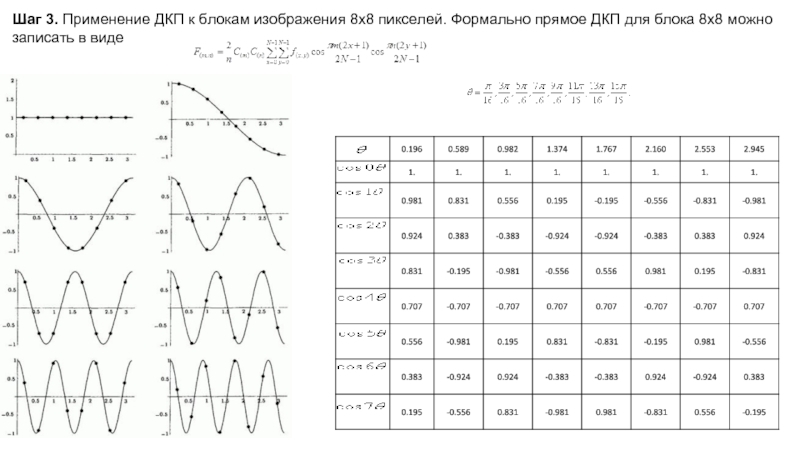
Слайд 10Шаг 3. Применение ДКП к блокам изображения 8х8 пикселей. Формально прямое ДКП
Слайд 11 Преобразование блока изображения f(x,y) в блок ДКП коэффициентовF(m,n):
а – блок изображения;
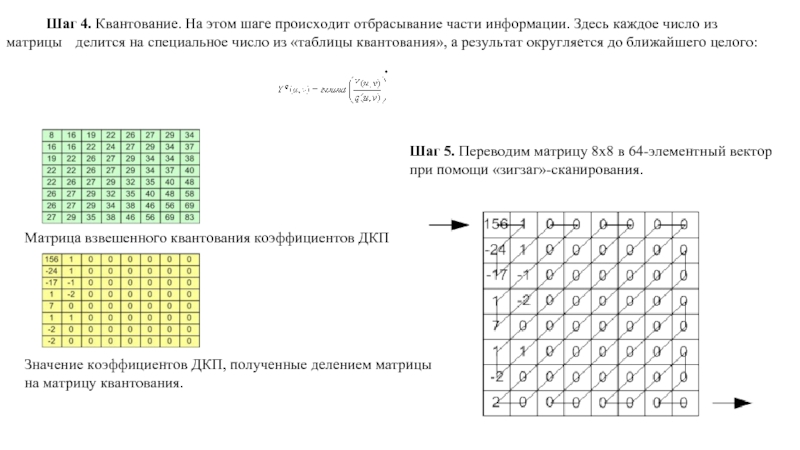
Слайд 12Шаг 4. Квантование. На этом шаге происходит отбрасывание части информации. Здесь каждое
.
Матрица взвешенного квантования коэффициентов ДКП
Значение коэффициентов ДКП, полученные делением матрицы на матрицу квантования.
Шаг 5. Переводим матрицу 8х8 в 64-элементный вектор при помощи «зигзаг»-сканирования.
Слайд 13Шаг 6. Преобразовываем вектор с помощью модифицированного алгоритма RLE, на выходе которого
Шаг 7. Свертываем получившиеся пары с помощью неравномерных кодов Хаффмана с фиксированной таблицей. Причем для DC и AC коэффициентов используются разные коды, т.е. разные таблицы с кодами Хаффмана.
Схема упорядочения DC коэффициентов
Слайд 14158 128 121 117 136 128 128 129 134 123 121
CHARACTER=158, код 1111
CHARACTER=128, код 1101
CHARACTER=121, код 1011
Слайд 16Рис. 1. Элементы матрицы квантования в графических файлах
Рис. 2. Различная
Рис. 3 Информация EXIF файла, обработанного программой «Adobe Photoshop CS3.
Слайд 18Анализ ошибки сжатия
Двойной эффект квантования (Double quantization effect)
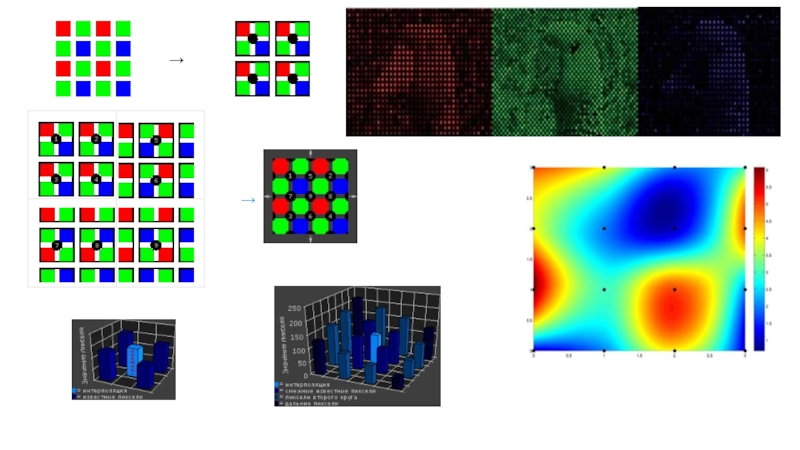
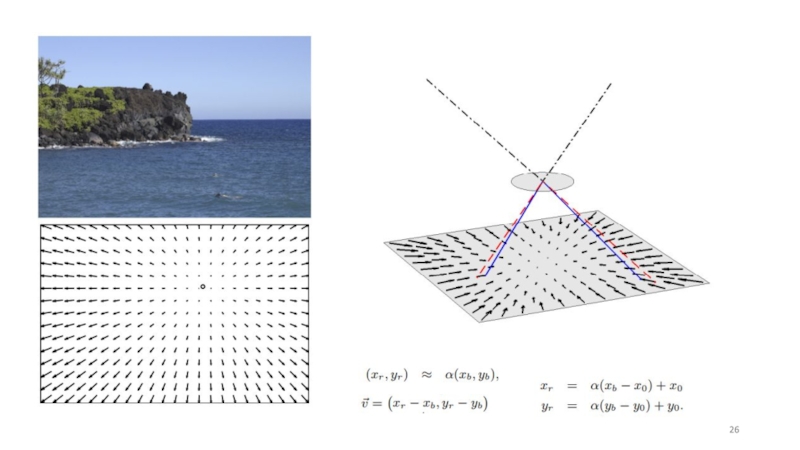
Анализ пиксельных связей (Color
Анализ хроматических аберраций
Анализ функции отклика фотоаппарата
Анализ границ блоков 8х8 ((Block artifact grid detection))
Анализ шумов
Стеганографические:
Критерий хи-квадрат
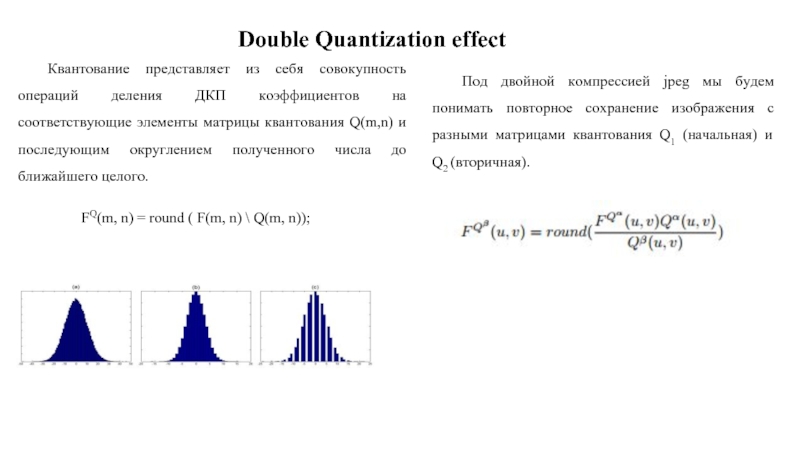
Слайд 20Double Quantization effect
FQ(m, n) = round ( F(m, n) \
Квантование представляет из себя совокупность операций деления ДКП коэффициентов на соответствующие элементы матрицы квантования Q(m,n) и последующим округлением полученного числа до ближайшего целого.
Под двойной компрессией jpeg мы будем понимать повторное сохранение изображения с разными матрицами квантования Q1 (начальная) и Q2 (вторичная).