- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
AES стандарты. Rijndael алгоритмі. (Дәріс 6) презентация
Содержание
- 1. AES стандарты. Rijndael алгоритмі. (Дәріс 6)
- 2. Енді Rijndael алгоритмін сипаттауға көшеміз. Алгоритмді сипаттау
- 3. Жағдай және кілт Nb = 6 байт
- 4. Сызықты емес байттық ауысу. Әрбір байтқа GF(28)
- 5. SybBytes түрлендіруі Жағдайға SubBytes түрлендіруін қолданудың жалпы
- 6. Жолды жылжыту. Әртүрлі мөлшерге тікбұрышты массивтің үш
- 7. ShiftRows түрлендіруі ShiftRows түрлендіру құрылымы Nb жағдай ұзындығына жылжыту шамасының тәуелділігі
- 8. Бағандарды алмастыру. 4-байттық векторды көрсететін бағандар 3-тен
- 9. MixColumns түрлендіруі MixColumns түрлендіруінің құрылымы MixColumns түрленуінің
- 10. Кілтті қосу жағдай массивінің әрбір байтын кілт
- 11. AddRoundKey түрлендіруі AddRoundKey түрлендіру құрылымы ағымды
- 12. Кілтті кеңейту механизмі Әрбір раундте өзінің әмбебап
- 13. Rijndael алгоритмінде бағандарды алмастырудың қосымша операциясын қарастрайық.
- 15. Мұнда a15 = 1 болатынын ескеру керек.
Слайд 2Енді Rijndael алгоритмін сипаттауға көшеміз. Алгоритмді сипаттау кезінде x8 + x4
Әрбір итерация 4 түрлендіруден тұрады: сызықты емес байттық ауысу, жолды жылжыту, бағандарды алмастыру, кілтті қосу. Осы операцияларды толығырақ қарастырайық.
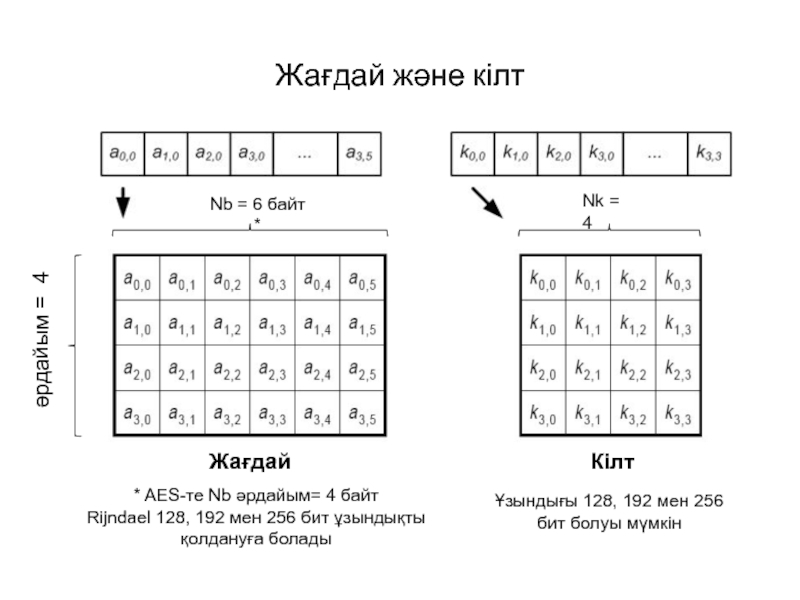
Слайд 3Жағдай және кілт
Nb = 6 байт *
Nk = 4
әрдайым = 4
Жағдай
Кілт
* AES-те Nb әрдайым= 4 байт
Rijndael 128, 192 мен 256 бит ұзындықты қолдануға болады
Ұзындығы 128, 192 мен 256 бит болуы мүмкін
Слайд 4Сызықты емес байттық ауысу. Әрбір байтқа GF(28) өрісінде көбейту бойынша кері
b(x) = (x7+x6+x2+x)+a(x)(x7+x6+x5+x4+1) mod (x8+1)
немесе матрицалық формада
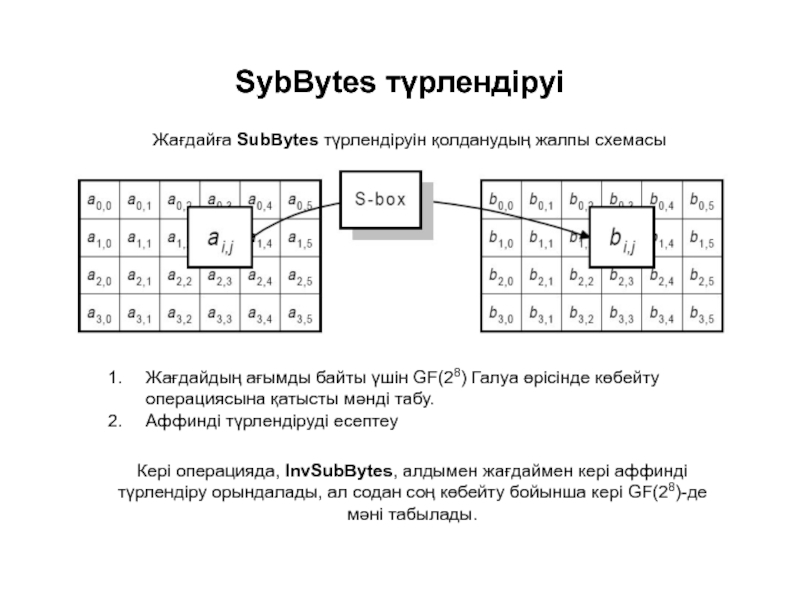
Слайд 5SybBytes түрлендіруі
Жағдайға SubBytes түрлендіруін қолданудың жалпы схемасы
Жағдайдың ағымды байты үшін GF(28)
Аффинді түрлендіруді есептеу
Кері операцияда, InvSubBytes, алдымен жағдаймен кері аффинді түрлендіру орындалады, ал содан соң көбейту бойынша кері GF(28)-де мәні табылады.
Слайд 6Жолды жылжыту.
Әртүрлі мөлшерге тікбұрышты массивтің үш соңғы жолын сол жаққа циклдік
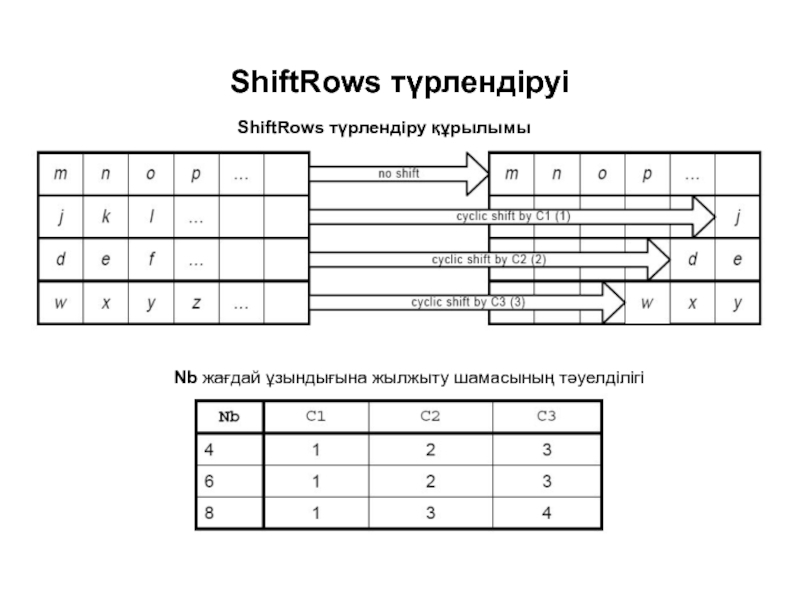
Слайд 7ShiftRows түрлендіруі
ShiftRows түрлендіру құрылымы
Nb жағдай ұзындығына жылжыту шамасының тәуелділігі
Слайд 8Бағандарды алмастыру.
4-байттық векторды көрсететін бағандар 3-тен аспайтын дәрежелі полином ретінде GF(28)-нен
c(x) ='00000011'x3+'00000001'x2+'00000001'x+'00000010'.
c(x) x4 +1-пен өзара қарапайым болып табылады. c(x)-ке кері полином мынаған тең
d(x)='00001011'x3+'00001101'x2+'00001001'x+'00001110'.
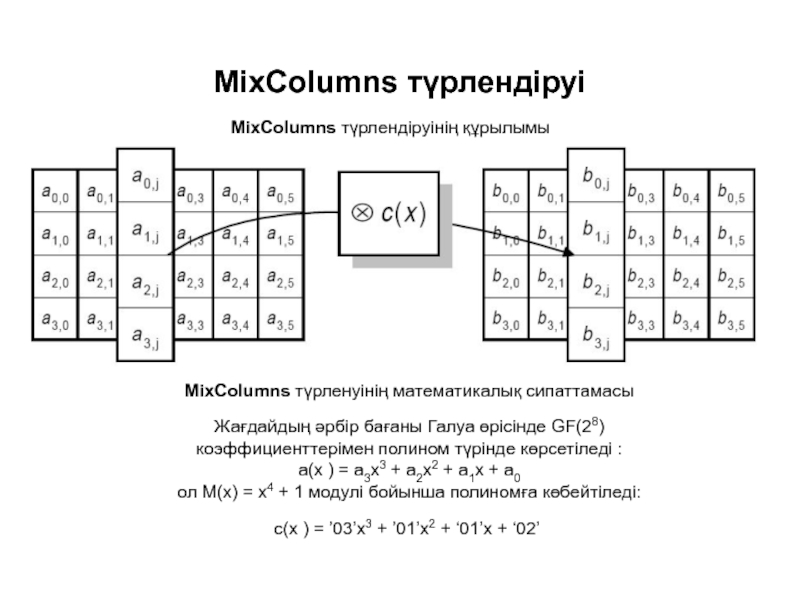
Слайд 9MixColumns түрлендіруі
MixColumns түрлендіруінің құрылымы
MixColumns түрленуінің математикалық сипаттамасы
Жағдайдың әрбір бағаны Галуа
a(x ) = a3x3 + a2x2 + a1x + a0
ол M(x) = x4 + 1 модулі бойынша полиномға көбейтіледі:
c(x ) = ’03’x3 + ’01’x2 + ‘01’x + ‘02’
Слайд 10Кілтті қосу жағдай массивінің әрбір байтын кілт массивінің сәйкес байтымен екі
Rijndael алгоритмінің ерекшелігі – әрбір итерацияда барлық блок өзгеріске ұшырайды, сондай-ақ түрлендіру жол мен баған бойынша екі өлшемде орындалады. Соңғысы екі итерацияда ақпаратты толық шашыратып және араластыруға кепіл береді. Шашырату болып ашық мәтіннің бір биті шифрмәтіннің бірнеше битіне әсер етуі керек екендігімен түсіндіріледі. Минималды ерекшелігі бар ашық мәтіннің екі блогын шифрлеу кезінде шифрмәтіннің бір біріне ұқсас емес блоктары алынуы керек. Араластыру болып шифр алғашқы мәтін символдары арасында тәуелділікті жасыруы түсіндіріледі.
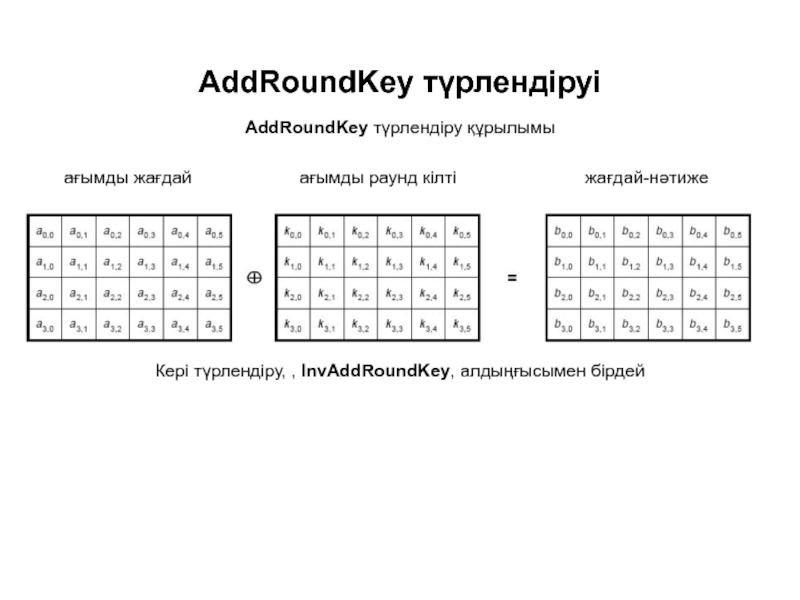
Слайд 11AddRoundKey түрлендіруі
AddRoundKey түрлендіру құрылымы
ағымды жағдай
ағымды раунд кілті
жағдай-нәтиже
Кері түрлендіру, , InvAddRoundKey,
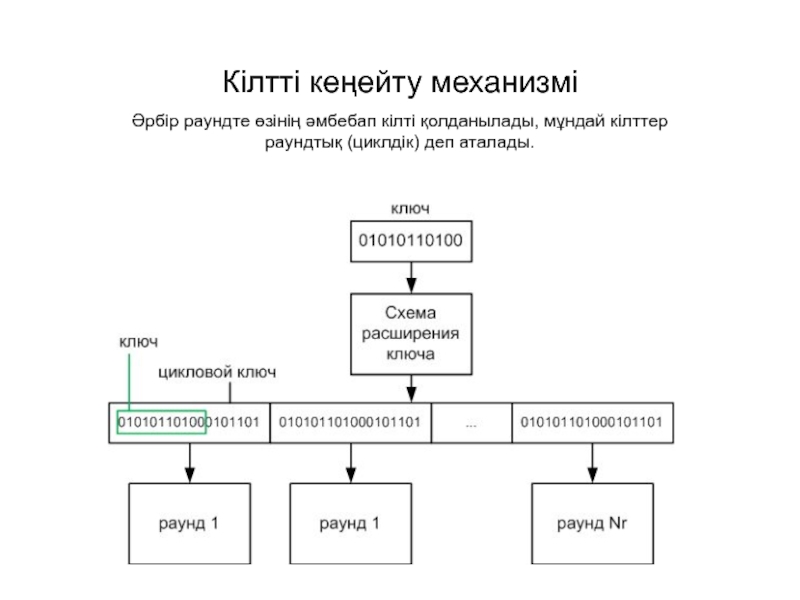
Слайд 12Кілтті кеңейту механизмі
Әрбір раундте өзінің әмбебап кілті қолданылады, мұндай кілттер раундтық
Слайд 13Rijndael алгоритмінде бағандарды алмастырудың қосымша операциясын қарастрайық. GF(28) өрісі көп элементтен
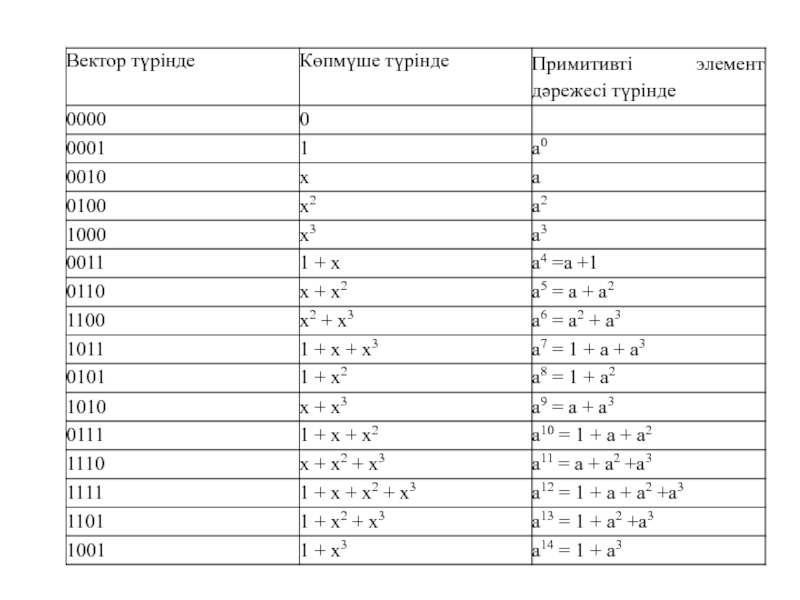
x4 + x +1 модулі бойынша GF(24) өрісін тұрғызайық. Оның элементтері көрсетудің келесі формаларына ие:
Слайд 15Мұнда a15 = 1 болатынын ескеру керек.
Баған a(x) ='1110' x+'1010‘ түріне
Көбейтуді GF(24) өрісінің примитивті элемент дәрежесі түрінде a(x) және c(x) коэффициенттер көрсетілуін пайдалана отырып орындауға болады. Онда
a(x)c(x)mod(x2 +1) = (a11 x + a9)(a4 x + 1)mod(x2 +1) =
= a15 x2 + (a13 +a11)x + a9 mod(x2 +1) = x2 + (1 + a2 +a3 +a + a2 +a3)x + a9 mod(x2 +1) = = x2 + a4 x + a9 mod(x2 +1) = a4 x + a9 +1 ='0011'x+'1011'.
Барлық қосу 2 модулі бойынша орындалады.
Көбейту a(x) және c(x) полиномы коэффициенттерінің полиномиальді көрсетілімін пайдалана отырып орындауға болады. Шатасып кетпеу үшін х формальді айнымалысын коэффициенттерді полиномиальді көрсетілімде у айнымалысына алмастырамыз. Онда мынаны аламыз:
a(x)c(x)mod(x2+1)=((y3+y2+y)x+(y3+y))((y+1)x+1)mod(x2+1)=
=(y4+y3+y2+y3+y2+y)x2+(y3+y2+y+y4+y2+y3+y)x+(y3+y)mod(x2+1)=
=(y4+y)x2+y4x+(y3+y)mod(x2+1)=x2+(y+1)x+(y3+y)mod(x2+1)=
=(y+1)x+(y3+y+1)='0011'x+'1011'.