несамопроизвольные процессы. Второй закон термодинамики.
Энтропия как критерий самопроизвольности процесса в изолированной системе.
Энергия Гиббса и Гельмгольца как критерий самопроизвольности в закрытых и открытых системах.
Критерии направленности процессов в системах переменного состава. Химический потенциал.
Лектор: доцент кафедры химии
Григорьева Марина Викторовна
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Второй закон термодинамики презентация
Содержание
- 1. Второй закон термодинамики
- 2. 1. Самопроизв. и несамопроизв. процессы. 2-й з-н
- 3. 1. Самопроизв. и несамопроизв. процессы. 2-й з-н термодинамики
- 4. 1. Самопроизв. и несамопроизв. процессы. 2-й з-н
- 5. 1. Самопроизв. и несамопроизв. процессы. 2-й з-н термодинамики
- 6. 1. Самопроизв. и несамопроизв. процессы. 2-й з-н
- 7. 1. Самопроизв. и несамопроизв. процессы. 2-й з-н
- 8. 1. Самопроизв. и несамопроизв. процессы. 2-й з-н
- 9. 2. Энтропия как критерий самопроиз-ти процесса в
- 10. 2. Энтропия как критерий самопроиз-ти процесса в
- 11. 2. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
- 12. 2. Энтропия как критерий самопроизвольности процесса в
- 13. 2. Энтропия как критерий самопроиз-ти процесса в
- 14. 2. Энтропия как критерий самопроиз-ти процесса в
- 15. 2. Энтропия как критерий самопроиз-ти процесса в
- 16. 2. Энтропия как критерий самопроиз-ти процесса в
- 17. 2. Энтропия как критерий самопроиз-ти процесса в
- 18. 2. Энтропия как критерий самопроиз-ти процесса в
- 19. 2. Энтропия как критерий самопроиз-ти процесса в
- 20. 2. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
- 21. 2. Энтропия как критерий самопроиз-ти процесса в
- 22. 3. Энергия Гиббса и Гельмгольца
- 23. 3. Энергия Гиббса и Гельмгольца
- 24. 3. Энергия Гиббса и Гельмгольца
- 25. 3. Энергия Гиббса и Гельмгольца
- 26. 3. Энергия Гиббса и Гельмгольца
- 27. 4. Химический потенциал Химический потенциал
- 28. 4. Химический потенциал Наиболее просто
- 29. 4. Химический потенциал В простейшем
- 30. Спасибо за внимание!
Слайд 1ОМСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ХИМИИ
Лекция 3. Второй закон термодинамики
Самопроизвольные и
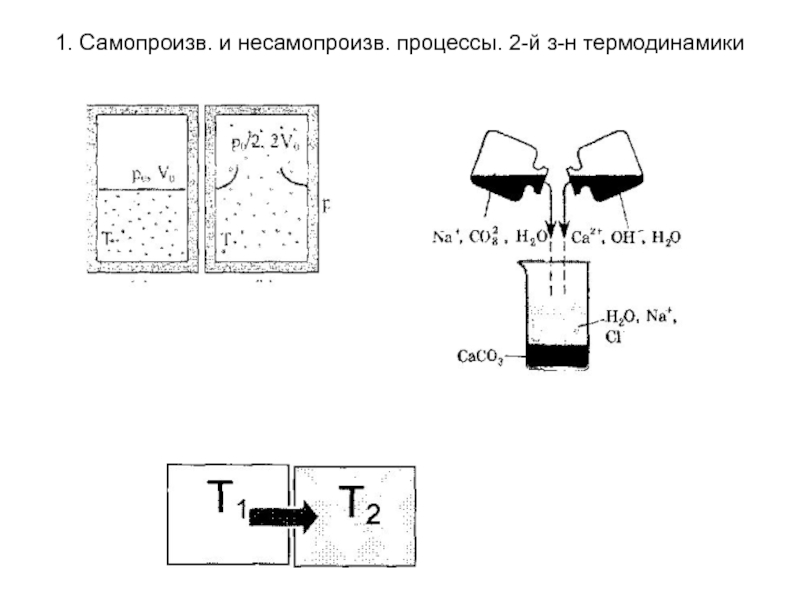
Слайд 21. Самопроизв. и несамопроизв. процессы. 2-й з-н термодинамики
Процессы подразделяются на самопроизвольные
и не самопроизвольные.
Самопроизвольные процессы - процессы протекающие без сообщения энергии системе извне. Они протекают до установления равновесия в термодинамической системе. К ним относят переход теплоты от горячего тела к холодному, расширение газа при подвижных границах раздела система -среда, реакции протекающие с выпадением осадка, реакции протекающие с выделением газа и т.д. За счет самопроизвольных процессов может быть совершена работа: например, за счет разности давлений можно получить механическую работу; за счет разности температур может работать тепловой двигатель или термопара.
Самопроизвольные процессы - процессы протекающие без сообщения энергии системе извне. Они протекают до установления равновесия в термодинамической системе. К ним относят переход теплоты от горячего тела к холодному, расширение газа при подвижных границах раздела система -среда, реакции протекающие с выпадением осадка, реакции протекающие с выделением газа и т.д. За счет самопроизвольных процессов может быть совершена работа: например, за счет разности давлений можно получить механическую работу; за счет разности температур может работать тепловой двигатель или термопара.
Слайд 41. Самопроизв. и несамопроизв. процессы. 2-й з-н термодинамики
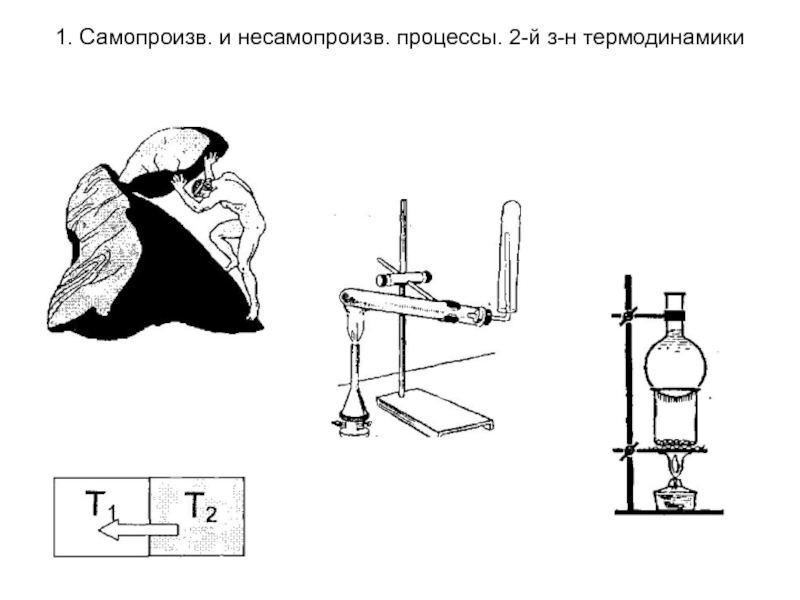
Несамопроизвольные процессы - процессы
протекающие при сообщении системе энергии извне. В результате таких процессов система удаляется от состояния равновесия. Примерами таких процессов служит подъем тела в гору («сизифов труд»), переход теплоты от более холодного тела к более нагретому (в холодильных машинах), разложение воды на водород и кислород , разложение перманганата калия, возгонка нафталина и т.д.
Слайд 61. Самопроизв. и несамопроизв. процессы. 2-й з-н термодинамики
Первый закон
термодинамики не дает ответа на вопрос «Что является критерием самопроизвольности процесса?»
Данные критерии определяются 2-м законом термодинамики.
2-й закон термодинамики как и 1-й, является постулатом. Его справедливость подтверждается опытами. Основоположниками закона являются С. Карно, Р.Клаузис, У.Томсон, Дж. Максвелл и др. Сначала закон был сформулирован как основной закон действия тепловых машин, затем его границы расширились до объяснения физико-химических процессов.
Данные критерии определяются 2-м законом термодинамики.
2-й закон термодинамики как и 1-й, является постулатом. Его справедливость подтверждается опытами. Основоположниками закона являются С. Карно, Р.Клаузис, У.Томсон, Дж. Максвелл и др. Сначала закон был сформулирован как основной закон действия тепловых машин, затем его границы расширились до объяснения физико-химических процессов.
Слайд 71. Самопроизв. и несамопроизв. процессы. 2-й з-н термодинамики
Предложено много разнообразных качественных
формулировок 2-го начала термодинамики:
теплота не может переходить сама собой от менее нагретого тела к более нагретому. (Р. Клаузиус, 1850)
невозможно превратить в механическую работу теплоту какого-либо тела, не произведя никакого другого действия, кроме охлаждения этого тела (Кельвин, 1854)
невозможен вечный двигатель второго рода, т.е. невозможно полное превращение теплоты в работу (В. Освальд, 1888).
теплота не может переходить сама собой от менее нагретого тела к более нагретому. (Р. Клаузиус, 1850)
невозможно превратить в механическую работу теплоту какого-либо тела, не произведя никакого другого действия, кроме охлаждения этого тела (Кельвин, 1854)
невозможен вечный двигатель второго рода, т.е. невозможно полное превращение теплоты в работу (В. Освальд, 1888).
Слайд 81. Самопроизв. и несамопроизв. процессы. 2-й з-н термодинамики
Количественно второй
закон термодинамики можно сформулировать так: существуют некие функции состояния системы - термодинамические потенциалы, по значению изменения которых можно определить возможность, направление и предел протекания самопроизвольного процесса.
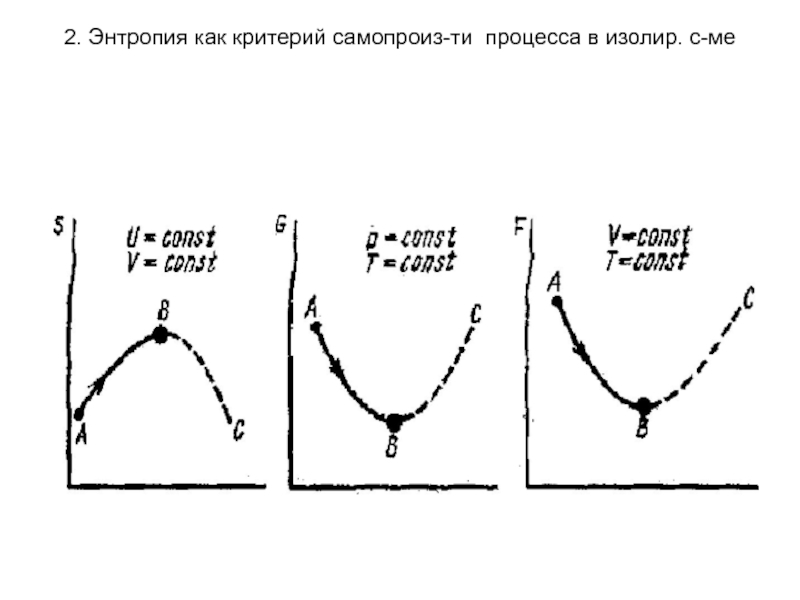
Слайд 92. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Термодинамическими
потенциалами являются различные функции состояния в зависимости от вида термодинамической системы:
для изолированной системы (при U=const, V= const) критерием самопроизвольности процесса является энтропия (S). Процесс протекает самопроизвольно, если ΔS> 0, будет протекать не самопроизвольно, если ΔS< 0, в момент равновесия ΔS = 0. В неизолированной системе энтропия может уменьшаться но при этом должен происходить рост энтропии в окружающей среде.
для изолированной системы (при U=const, V= const) критерием самопроизвольности процесса является энтропия (S). Процесс протекает самопроизвольно, если ΔS> 0, будет протекать не самопроизвольно, если ΔS< 0, в момент равновесия ΔS = 0. В неизолированной системе энтропия может уменьшаться но при этом должен происходить рост энтропии в окружающей среде.
Слайд 102. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
для закрытой системы
(при T=const, V= const) критерием самопроизвольности процесса является энергия Гельмгольца (F). ΔF=0 - равновесие;
ΔF< 0 - самопроизвольный процесс;
ΔF>0 – не самопроизвольный процесс.
для открытой системы (при T=const, р= const) критерием самопроизвольности процесса является энергия Гиббса (G). ΔG=0 - равновесие;
ΔG< 0 - самопроизвольный процесс;
ΔG >0 - не самопроизвольный процесс.
ΔF< 0 - самопроизвольный процесс;
ΔF>0 – не самопроизвольный процесс.
для открытой системы (при T=const, р= const) критерием самопроизвольности процесса является энергия Гиббса (G). ΔG=0 - равновесие;
ΔG< 0 - самопроизвольный процесс;
ΔG >0 - не самопроизвольный процесс.
Слайд 122. Энтропия как критерий самопроизвольности процесса в изолированной системе
Термодинамическое определение энтропии
введено Р. Клаузиусом в 1865г . На основе изучения процессов превращения теплоты в работу, происходящих в тепловой машине (нагреватель - рабочее тело - холодильник), он вывел, что существует некоторое экстенсивное свойство системы S, называемое энтропией, которое может служить мерой рассеивания энергии при переходе теплоты в работу.
Слайд 132. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Приращение
энтропии в равновесном процессе равно приведенной теплоте – отношению элементарного количества теплоты к температуре.
Энтропия является функцией состояния системы, следовательно изменение энтропии зависит от начального и конечного состояния системы и не зависит от пути процесса: ΔS = S2-S1
Энтропия является функцией состояния системы, следовательно изменение энтропии зависит от начального и конечного состояния системы и не зависит от пути процесса: ΔS = S2-S1
Слайд 142. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Статистическое определение энтропии
в 1896 г дает Л. Больцман. В связи с тем, что теплота, связана с идеей хаотического движения молекул, следовательно можно определить физический смысл энтропии на основе представлений молекулярной статистики.
Слайд 152. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Макросостояние системы характеризуется
определенными термодинамическими параметрами , в т.ч. и энтропией. Микросостояние системы определяется энергией и положением каждой частицы. Макросостояние системы может существовать при различном расположении и разной энергии частиц определяющих микросостояние. Число микросостояний, которое соответствует данному макросостоянию вещества, называется термодинамической вероятностью W. Например, для системы состоящей из 10 частиц W=12600.
Слайд 162. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Больцман установил
взаимосвязь энтропии с термодинамической вероятностью:
S= КБ In W ,где КБ - постоянная Больцмана (КБ = R/NA= 1,38 ·10-23 Дж/ моль),
Энтропия - мера наиболее вероятностного состояния системы, а следовательно и мера беспорядка (хаотичности) системы.
S= КБ In W ,где КБ - постоянная Больцмана (КБ = R/NA= 1,38 ·10-23 Дж/ моль),
Энтропия - мера наиболее вероятностного состояния системы, а следовательно и мера беспорядка (хаотичности) системы.
Слайд 172. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
При абсолютном нуле
прекращаются колебательные движения частиц, образующих кристаллическую решетку. Такое микросостояние достигается лишь при одном варианте расположения микрочастиц (W) и в соответствии с формулой Больцмана:
S = КБ In 1 = 0
Эта закономерность известна как третий закон термодинамики (постулат Планка): при абсолютном нуле энтропия чистого вещества равна нулю.
S = КБ In 1 = 0
Эта закономерность известна как третий закон термодинамики (постулат Планка): при абсолютном нуле энтропия чистого вещества равна нулю.
Слайд 182. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Расчет абсолютного значения
энтропии
Для многих практических целей, особенно для расчета химических равновесий, надо знать стандартные энтропии веществ S°. Для их вычисления используют табличные данные теплоемкости, определенные при возможно низких температурах и теплоты фазовых переходов. Значение теплоемкости вблизи абсолютного нуля находят путём экстраполяции. Если в интервале температур от 0 до Т вещество претерпевает ф.п., то они должны быть учтены.
Для многих практических целей, особенно для расчета химических равновесий, надо знать стандартные энтропии веществ S°. Для их вычисления используют табличные данные теплоемкости, определенные при возможно низких температурах и теплоты фазовых переходов. Значение теплоемкости вблизи абсолютного нуля находят путём экстраполяции. Если в интервале температур от 0 до Т вещество претерпевает ф.п., то они должны быть учтены.
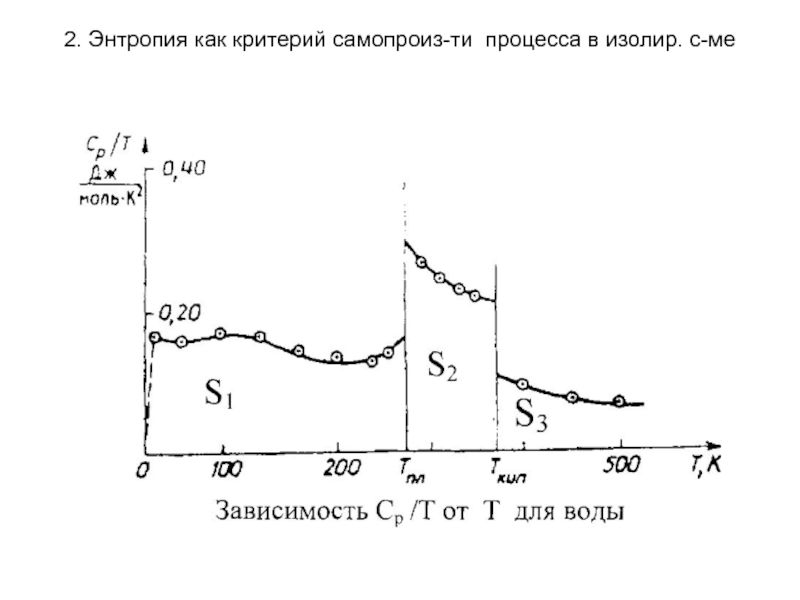
Слайд 192. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Где S0ид -
поправка на неидеальность газа (пара) при данной температуре.
Расчет энтропии осуществляется графически: каждый интеграл равен соответствующей площади.
Расчет энтропии осуществляется графически: каждый интеграл равен соответствующей площади.
Слайд 212. Энтропия как критерий самопроиз-ти процесса в изолир. с-ме
Сложив
сумму этих интегральных членов с изменениями энтропии при всех фазовых переходах в исследуемом интервале температур (от О К до Т К) и с поправкой на неидеальность, находят значение абсолютной энтропии данного вещества при температуре Т.
Слайд 223. Энергия Гиббса и Гельмгольца
При Т,р =const (изохорно-изотермические условия)
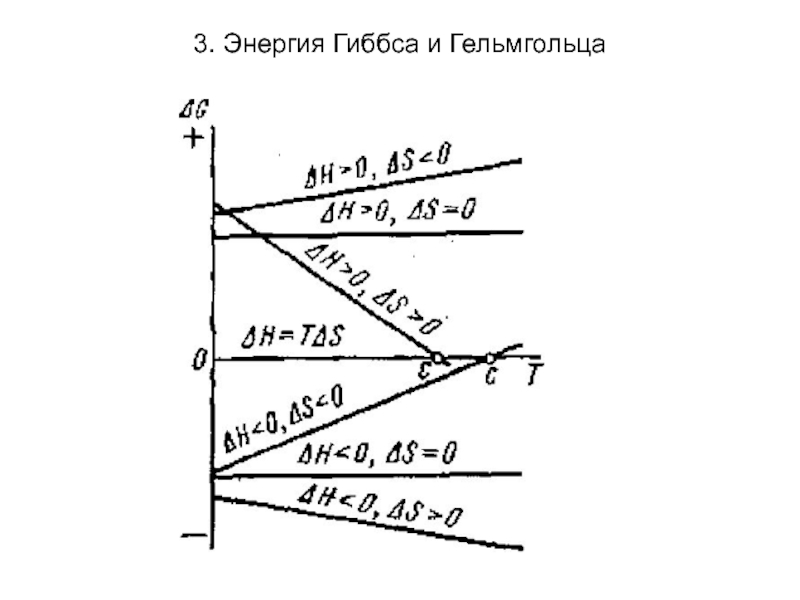
критерием самопроизвольности является изобарно-изотермический потенциал (энергия Гиббса) G = Н - TS (ΔG = ΔН -TΔS).
При ΔG=0 -равновесие;
ΔG<0 самопроизвольный процесс;
ΔG>0 – не самопроизвольный процесс.
Знак и величина ΔG определяется энтальпий-ным ΔН и энтропийным факторами TΔS. Возможные случаи зависимости энтальпийного и энтропийного фактора:
При ΔG=0 -равновесие;
ΔG<0 самопроизвольный процесс;
ΔG>0 – не самопроизвольный процесс.
Знак и величина ΔG определяется энтальпий-ным ΔН и энтропийным факторами TΔS. Возможные случаи зависимости энтальпийного и энтропийного фактора:
Слайд 253. Энергия Гиббса и Гельмгольца
При T,V = const, критерием
самопроизвольности является изохорно-изотермический потенциал (энергия Гельмгольца) F = U -TS (ΔF = ΔU -TΔS).
Слайд 263. Энергия Гиббса и Гельмгольца
Характеристические функции - функции, частные
производные которых по какому-либо из параметров (естественной переменной) равны другому параметру. Энергия Гиббса относится к характеристическим функциям.
Слайд 274. Химический потенциал
Химический потенциал μ – термодинамическая функция состояния,
определяющая изменение термодинамических потенциалов при изменении числа частиц в системе и необходимая для описания свойств открытых систем (с переменным числом частиц).
Слайд 284. Химический потенциал
Наиболее просто химический потенциал связан с термодинамическим
потенциалом G: G=∑μi Ni .
Для однокомпонентной системы
μ = G/N, т. е. представляет собой энергию Гиббса, отнесённую к одной частице.
Для однокомпонентной системы
μ = G/N, т. е. представляет собой энергию Гиббса, отнесённую к одной частице.
Слайд 294. Химический потенциал
В простейшем случае идеальных газов зависит только
от концентрации i -го компонента:
μi = μi0+ kT ln С
μi = μi0+ kT ln С