- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
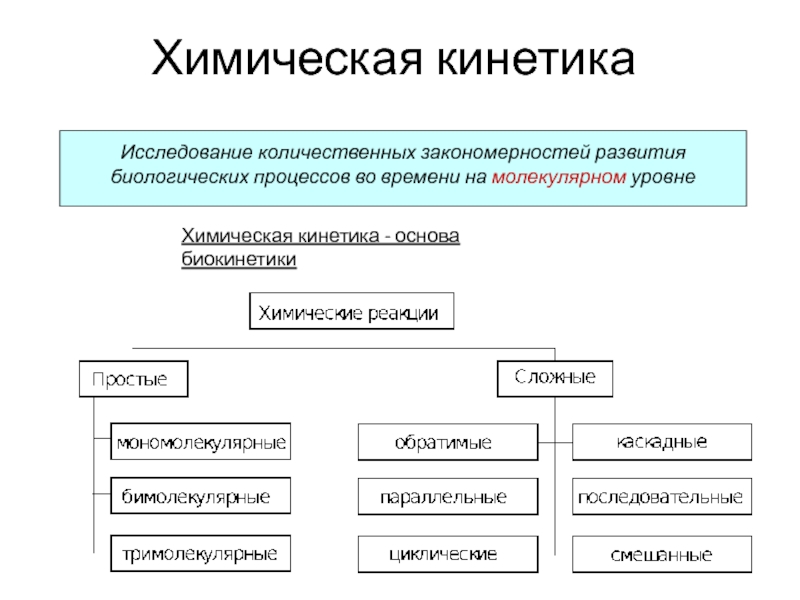
Лекция 9-10. Диффузионная кинетика презентация
Содержание
- 1. Лекция 9-10. Диффузионная кинетика
- 2. Математическое описание каталитического процесса на пористом зерне катализатора
- 3. Если химическая реакция протекает достаточно быстро, то
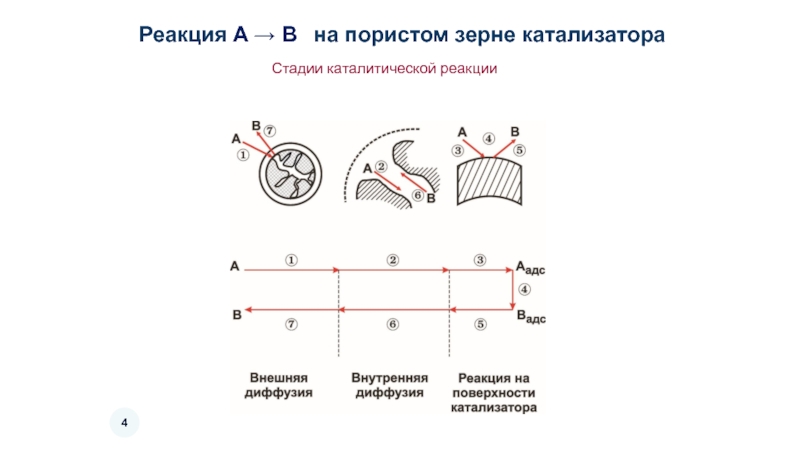
- 4. Стадии каталитической
- 5. Концентрационные профили в грануле пористого катализатора при
- 6. Внешняя диффузия – ограниченное число группы реакций
- 7. Влияние процессов переноса на скорость реакции
- 8. Диффузионный поток JD в неподвижной среде
- 9. . JD
- 10. . Степень использования внутренней поверхности зерна
- 11. Внутренняя пористая структура зерна катализатора
- 13. U
- 14. Нормальная (молекулярная) диффузия – если диаметр пор
- 15. Кнудсеновская диффузия – для тонких пор, диаметр
- 17. Экспериментальные методы определения коэффициентов внутренней диффузии
- 18. Вычисление молекулярного коэффициента диффузии для смеси
- 19. Бинарные коэффициенты диффузии (Уравнение Фуллер-Шеттлер-Гиддингс)
- 21. Зависимость бинарных коэффициентов диффузии от температуры
- 22. Вычисление кнудсеновского коэффициента диффузии
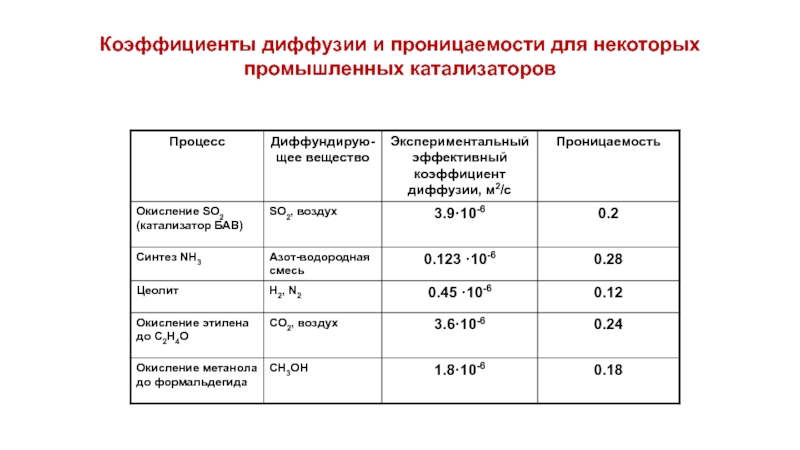
- 23. Коэффициенты диффузии и проницаемости для некоторых промышленных катализаторов
- 24. Модельные формы зерен катализатора
- 25. Математическая модель процесса в пористом изотермическом зерне
- 29. Скорость химической реакции (Отнесена к единице поверхности, размерность длина/время)
- 30. Уравнение материального баланса по компоненту А при
- 32. Введем обозначение степени использования катализатора через
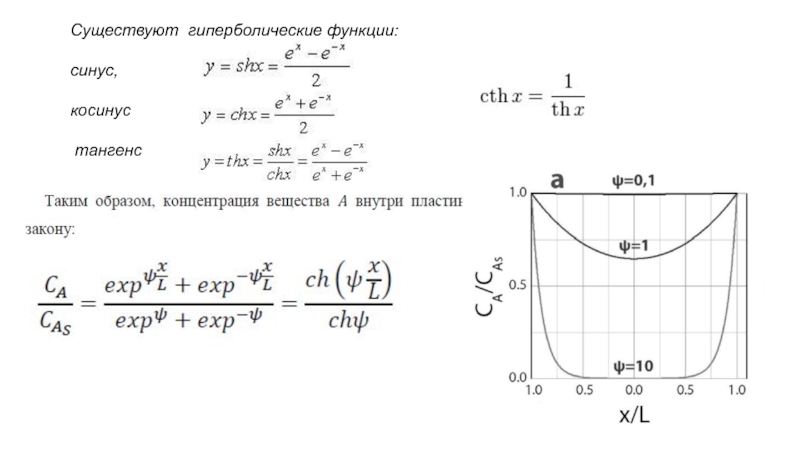
- 33. Существуют гиперболические функции: синус, косинус тангенс
- 34. Степень использования поверхности катализатора WН WН
- 35. Рис. – Зависимость степени использования катализатора ?
- 36. Для зерен катализатора любой формы Vз –
- 37. Оценка критерия Тиле Неподвижный слой
- 38. Изменение параметров кинетического уравнения при переходе из
- 39. Во внутридиффузионной области ? ≈ 1/
- 41. Зависимость скорости реакции окисления SO2 в SO3
- 42. Влияние внутренней диффузии Обратимые реакции
- 43. n1 > n2 - селективность
- 44. Оптимальная пористая структура Монодисперсная структура
- 45. Оптимальная пористая структура Почему размер пор
- 46. Оптимальная пористая структура Какой размер пор оптимален?
- 47. Оптимальная пористая структура Монодисперсная
- 48. Оптимальная пористая структура Монодисперсная структура
- 49. Оптимальная пористая структура При переходе
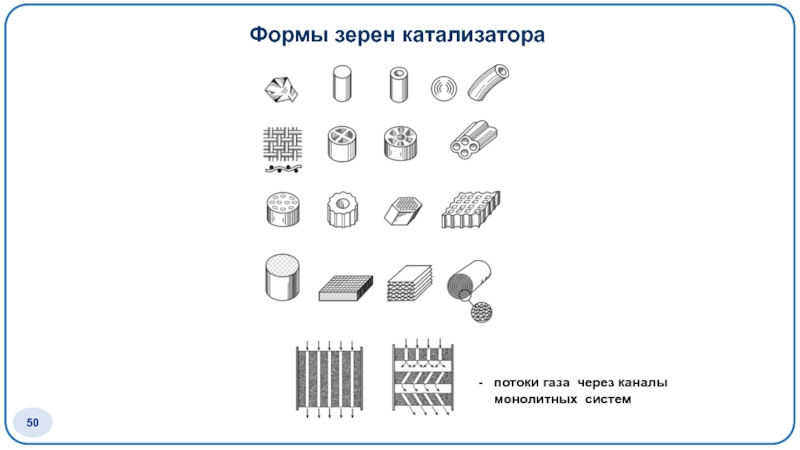
- 50. Формы зерен катализатора потоки газа через каналы монолитных систем
- 51. Катализаторы сложной формы H –
- 52. ЗАКЛЮЧЕНИЕ
Слайд 3Если химическая реакция протекает достаточно быстро, то скорость суммарного процесса катализа
Скоростью переноса массы реагентов или тепла и газовой (жидкой фазы) к внешней поверхности зерна катализатора – внешнедиффузионная область
Диффузией реагентов в порах зерна катализатора – внутриффузионная область
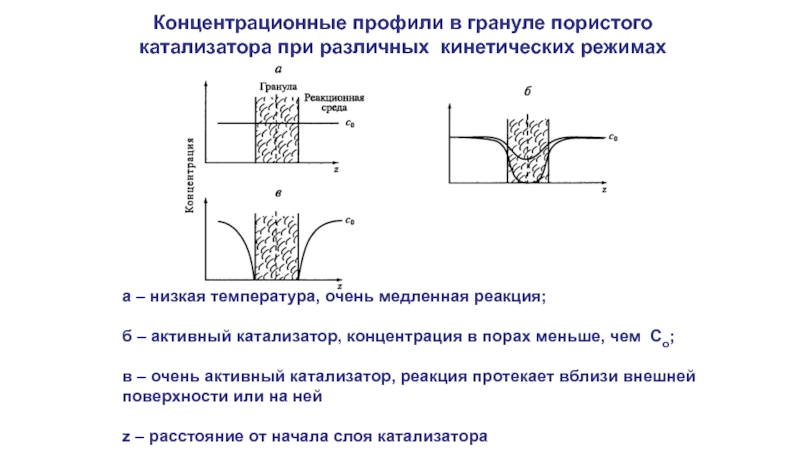
Слайд 5Концентрационные профили в грануле пористого катализатора при различных кинетических режимах
а –
б – активный катализатор, концентрация в порах меньше, чем Со;
в – очень активный катализатор, реакция протекает вблизи внешней поверхности или на ней
z – расстояние от начала слоя катализатора
Слайд 6Внешняя диффузия – ограниченное число группы реакций
Внутренняя диффузия оказывает существенное влияние
Кинетический режим – на всех участках поверхности раздела фаз концентрации реагирующих веществ и температура остаются постоянными, равными в объеме – в реальных условиях реализуется редко
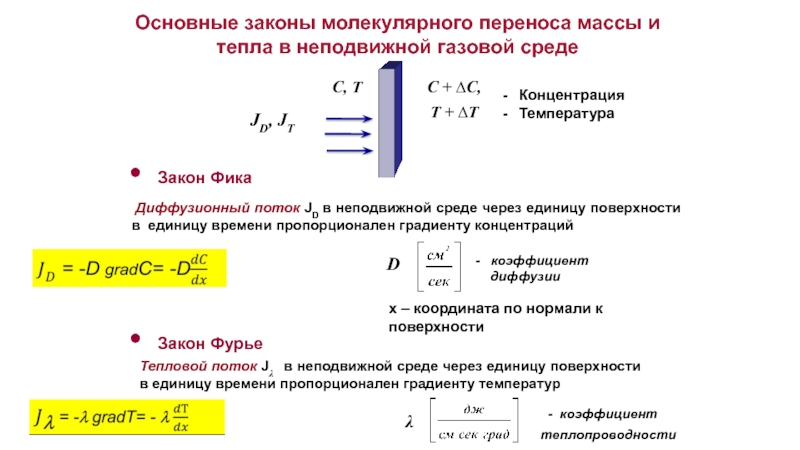
Слайд 8 Диффузионный поток JD в неподвижной среде через единицу поверхности в
Закон Фика
D
- коэффициент
диффузии
Закон Фурье
λ
- коэффициент
теплопроводности
Тепловой поток Jλ в неподвижной среде через единицу поверхности в единицу времени пропорционален градиенту температур
JD, JT
C + ∆C,
T + ∆T
C, T
Основные законы молекулярного переноса массы и тепла в неподвижной газовой среде
х – координата по нормали к поверхности
Концентрация
Температура
Слайд 10.
Степень использования внутренней поверхности зерна катализатора
Наблюдаемые скорости реакции - скорости
Wнабл. = f (C(y), T(y))
Кинетическая скорость реакции – скорость рассчитанная по концентрациям и температуре на поверхности зерна катализатора (Пренебрегаем массопереносом в приповерхностном слое)
Wкин. = f (Cп, Tп)
Степень использования внутренней поверхности зерна катализатора
Слайд 11Внутренняя пористая структура зерна катализатора
Размер внутренних образований:
1 нанометр – 1
Число внутренних образований:
109 – 1014 более мелких частиц
Корпускулярная модель
Глобулярная модель
К пористой системе можно применить общие статистические подходы и рассматривать зерно катализатора как гомогенную среду, в которой протекает реакция
со скоростью W, моль/(м3зерна·с),
а перенос вещества характеризуется эффективным коэффициентом диффузии Dэ, м2/c .
Квазигомогенная (или диффузионная) модель
Слайд 12
Перенос реагирующих веществ и продуктов реакции внутри зерен катализатора может осуществляться
Слайд 14Нормальная (молекулярная) диффузия – если диаметр пор превышает среднюю длину свободного
.
Слайд 15Кнудсеновская диффузия – для тонких пор, диаметр которых меньше средней длины
Слайд 16
В квазигомогенной модели диффузии в пористом зерне используется эффективный коэффициент диффузии
Dэф. = ПDi
П – коэффициент проницаемости зависит от геометрических характеристик пористой структуры.
Слайд 17Экспериментальные методы определения коэффициентов внутренней диффузии
Методы с химической реакцией
- экспериментальное
- расчет De при известной кинетике на основе математического описания
Стационарные методы
Нестационарные методы
создание стационарного градиента концентраций диффундирующего вещества с двух сторон пористой пластины катализатора
- измерение потока вещества через пластину
с одной стороны пластины создается скачок концентраций с1 , с другой
измеряется изменение во времени с(t), зависящее от De
- через пористую пластину катализатора пропускается газ-носитель, вводится газ- трассер, измеряется концентрация вещества- трассера на выходе из пластинки
→ V1 c1
V2 c2
Слайд 20
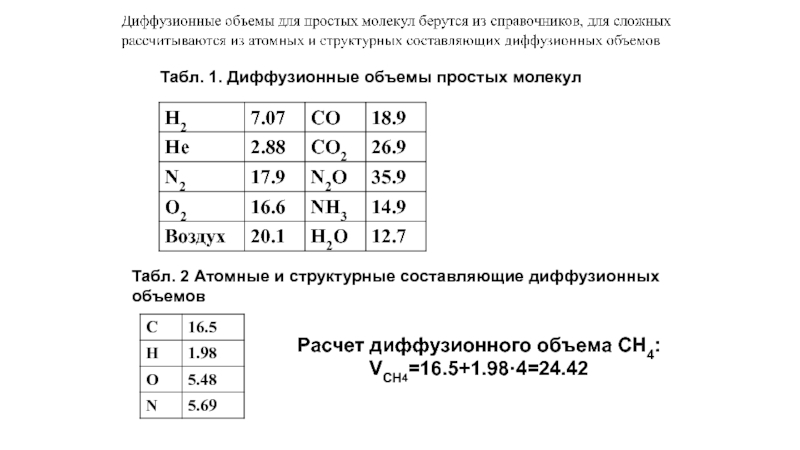
Табл. 1. Диффузионные объемы простых молекул
Табл. 2 Атомные и структурные составляющие
объемов
Расчет диффузионного объема CH4:
VCH4=16.5+1.98·4=24.42
Слайд 22Вычисление кнудсеновского коэффициента диффузии
Кнудсеновский коэффициент диффузии отражает соударение молекул со стенками
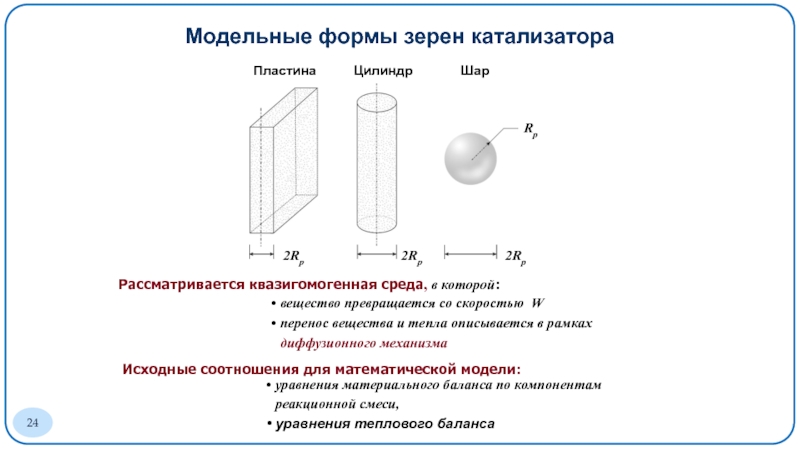
Слайд 24Модельные формы зерен катализатора
2Rp
2Rp
2Rp
Rp
уравнения материального баланса
уравнения теплового баланса
вещество превращается со скоростью W
перенос вещества и тепла описывается в рамках диффузионного механизма
Рассматривается квазигомогенная среда, в которой:
Исходные соотношения для математической модели:
Пластина
Цилиндр
Шар
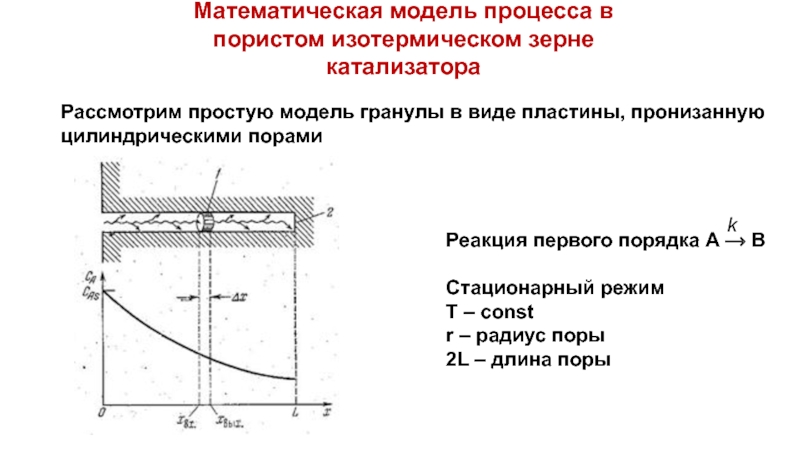
Слайд 25Математическая модель процесса в пористом изотермическом зерне катализатора
Рассмотрим простую модель гранулы
Реакция первого порядка А ⟶ В
Стационарный режим
Т – const
r – радиус поры
2L – длина поры
k
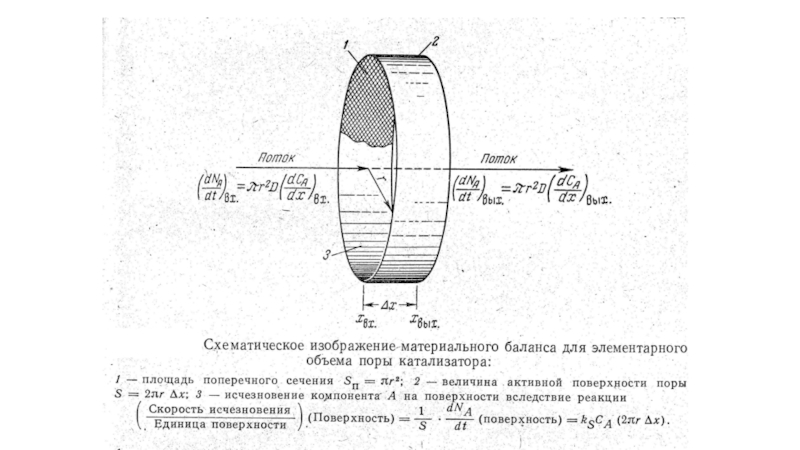
Слайд 30Уравнение материального баланса по компоненту А при стационарном состоянии системы
(деление на
Слайд 32
Введем обозначение степени использования катализатора через Ѱ – модуль Тиле
Модуль
nL=
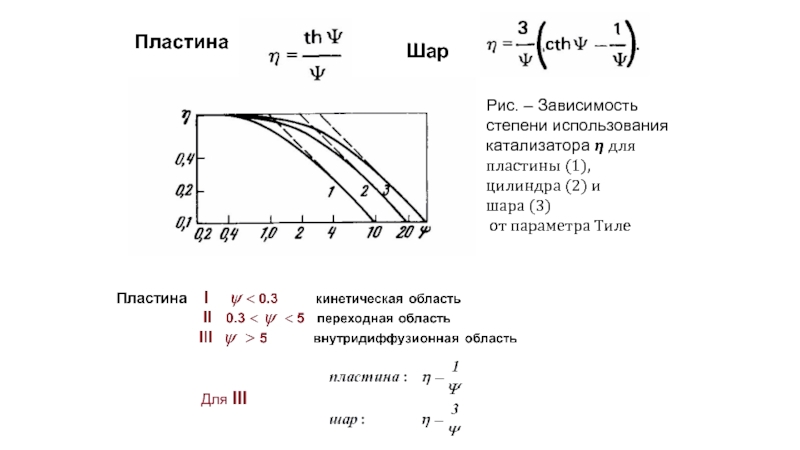
Слайд 35Рис. – Зависимость степени использования катализатора ? для пластины (1),
цилиндра (2)
шара (3)
от параметра Тиле
Пластина
Шар
Для III
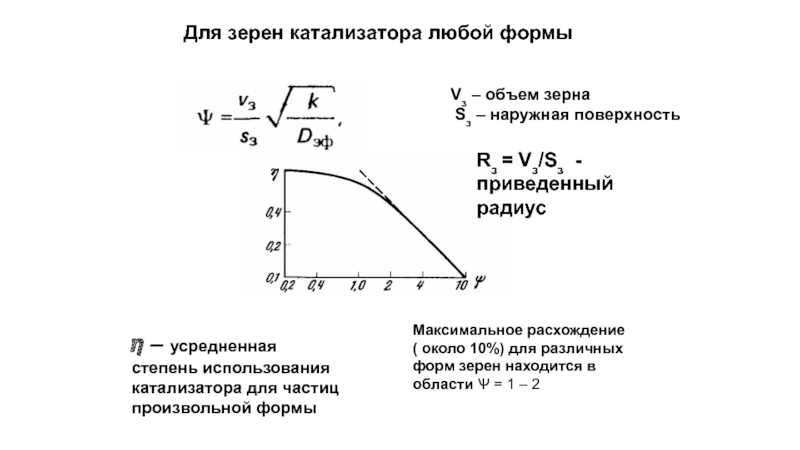
Слайд 36Для зерен катализатора любой формы
Vз – объем зерна
Sз – наружная
? – усредненная степень использования катализатора для частиц произвольной формы
Максимальное расхождение ( около 10%) для различных форм зерен находится в области Ѱ = 1 – 2
Rз = Vз/Sз - приведенный радиус
Слайд 37Оценка критерия Тиле
Неподвижный слой
Энергия активации
наблюдаемая скорость реакции равна:
т.е. наблюдаемая энергия активации равна:
Ψ ≈ 0.5 – 10
Псевдоожиженный слой
k ≈ 0.5 - 5 cек-1, Rp ≈ 100- 200 μм, De ≈ 0.03 - 0.1 cм2/сек,
Ψ < 0.01
во внутридиффузионной области
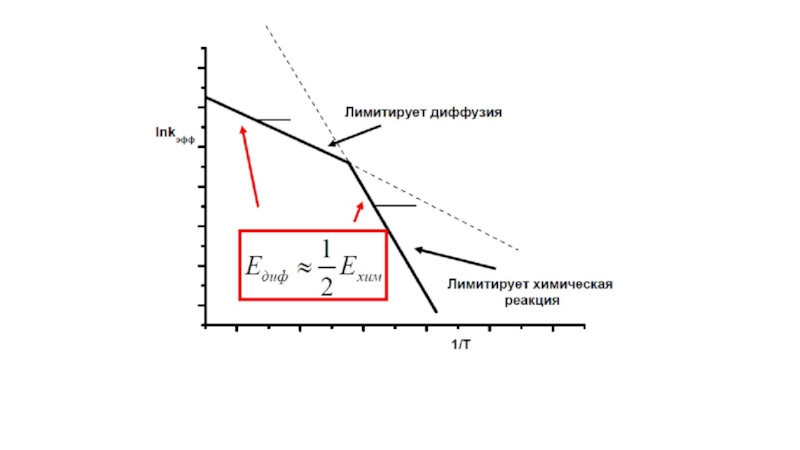
Слайд 38Изменение параметров кинетического уравнения при переходе из кинетической области во внутридиффузионную
Выразим
Слайд 39Во внутридиффузионной области
? ≈ 1/ Ѱ
Наблюдаемая скорость
w
Анализ уравнения показывает:
Во внутридиффузионной области порядок реакции по компоненту, концентрация которого в глубине зерна близка к нулю, становится средним между порядком реакции в кинетической области и первым порядком
Порядок реакции по остальным компонентам снижается в 2 раза
Наблюдаемая энергия активации становится равной половине энергии активации в кинетической области
Е = Екин./2 – зависимость Зельдовича
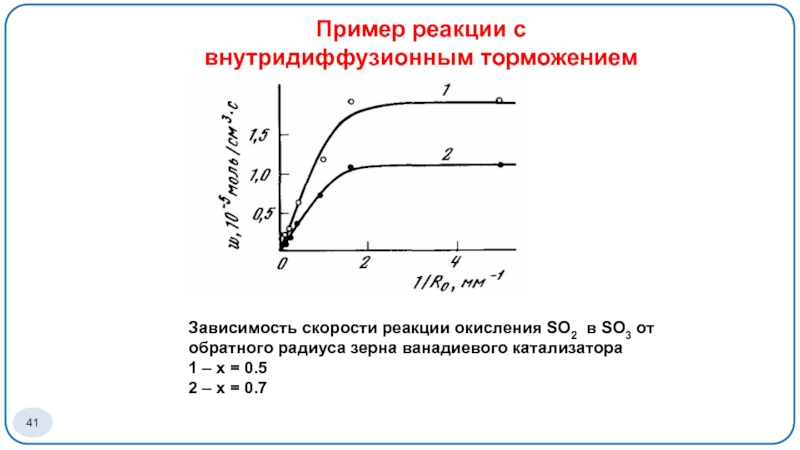
Слайд 41Зависимость скорости реакции окисления SO2 в SO3 от обратного радиуса зерна
1 – х = 0.5
2 – х = 0.7
Пример реакции с внутридиффузионным торможением
Слайд 42Влияние внутренней диффузии
Обратимые реакции
A B
wA
wA = k1 cA – k-1 cB; cA + cB = cs
Влияние диффузии сильнее, чем для необратимых реакций
Селективность - Сложные реакции
Cелективность по В для последовательной реакции всегда снижается в переходной и внутридиффузионной области
R = L
w2
w2
S = (w1 – w2)/w1 = (k1CA – k2CB) /k1CA = 1 – (k2/k1)(CB/CA)
Слайд 43n1 > n2 - селективность снижается
n1 < n2
n1 = n2 - нет изменения селективности
Диффузионное торможение в бóльшей степени снижает ту скорость реакции, которая быстрее уменьшается с ростом глубины превращения, т.е. чем выше порядок реакции
Параллельные реакции
w1
w1
w2
w2
S = W1 / (W1 + W2)
Слайд 44Оптимальная пористая структура
Монодисперсная структура
Монодисперсная структура состоит из микроглобул rmic
между микроглобулами гранулу пронизывают микропоры ρmic
Удельная внутренняя поверхность для гранулы произвольной формы оценивается по формуле:
ε - пористость зерна, rmic - размер микроглобулы, А – постоянная величина
rmic
Слайд 45Оптимальная пористая структура
Почему размер пор должен быть оптимальным?
При увеличении
- возрастает активность единицы объема катализатора
- внутренняя диффузия снижает скорость реакции
Реакция А → В
Удельная скорость реакции ws = ks с = a
Скорость реакции в объеме
Наблюдаемая скорость реакции
(на единицу поверхности)
Удельная внутренняя поверхность
A = 3 (для шара), ε = 0,7, rmic = 10 3 A0,
w = a Ss = ks Ss c = k с
wa
Слайд 46Оптимальная пористая структура
Какой размер пор оптимален?
Для простой экзотермической реакции А
Критерий Тиле равен
k = ks Ss ,
wa
Dk
Ре = П
Слайд 47Оптимальная пористая структура
Монодисперсная структура
1) Большие поры
Активность увеличивается при уменьшении размера пор до достижения области внутренней диффузии, рост активности прекращается при размере пор, близком к длине свободного пробега молекул
Оптимальный размер пор близок к длине свободного пробега молекул
Ss невысока Большая Ss
wa
Слайд 48Оптимальная пористая структура
Монодисперсная структура Бидисперсная структура
Бидисперсная структура
Бидисперсные структуры содержат поры двух размеров:
- макропоры радиуса rmac, пронизывающие зерно катализатора между макроглобулами;
- примыкающие к макропорам ответвления между микроглобулами - мезопоры
радиуса rmic .
rmic
rmic
rmac
2Rp
2Rp
Удельная поверхность определяется размером микроглобул rmic,
степень использования катализатора размером макроглобул rmac
rmic
Слайд 49
Оптимальная пористая структура
При переходе к бидисперсной структуре:
- активность катализатора
Переход к бидисперсным структурам целесообразен для процессов при небольших давлениях.
С увеличением давления эффективность бидисперсной структуры снижается
Оптимальный размер пор
Бидисперсная структура
Максимальная активность достигается, когда:
- упаковка микроглобул более плотная, т.е. хорошо развита поверхность в микропорах;
- макропоры обеспечивают молекулярный характер диффузии.
Реакция протекает в условиях, близких к кинетической области.
r
r
r
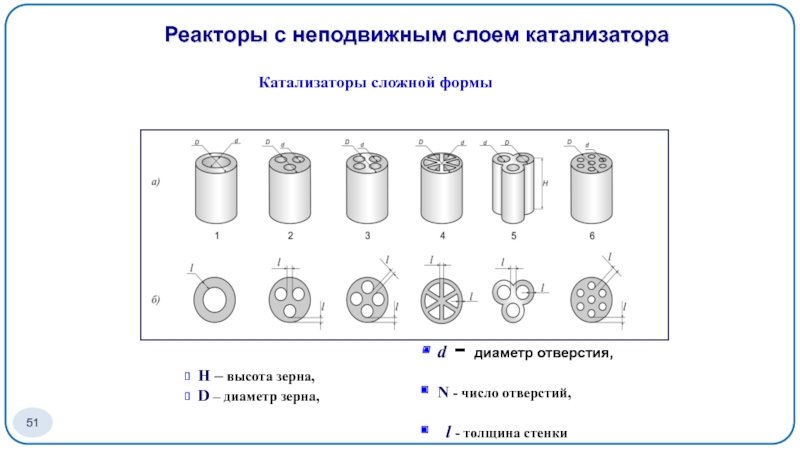
Слайд 51Катализаторы сложной формы
H – высота зерна,
D –
Реакторы с неподвижным слоем катализатора
d - диаметр отверстия,
N - число отверстий,
l - толщина стенки