- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Адсорбционные процессы. Кафедра технологии неорганических веществ и электрохимических процессов презентация
Содержание
- 1. Адсорбционные процессы. Кафедра технологии неорганических веществ и электрохимических процессов
- 2. СОДЕРЖАНИЕ КУРСА Введение Задачи и
- 3. СОДЕРЖАНИЕ КУРСА Введение Задачи и
- 4. Промышленные адсорбенты Характеристики промышленных адсорбентов. Активные
- 5. Кинетика адсорбции Предмет изучения, внешняя диффузия,
- 6. Технология и расчет адсорбционных процессов Основные этапы
- 7. Процессы осушки Технология процесса, адсорбенты-осушители, основное оборудование.
- 8. Основные понятия и определения
- 9. В однокомпонентных
- 10. Основные определения Адсорбция - поглощение частиц какого-либо
- 11. Обычно рассматривают адсорбцию компонентов газообразной
- 12. Сорбция, сорбент, сорбат, сорбтив – термины
- 13. Пусть исследуется некоторая совокупность объектов, каждому
- 14. Пусть исследуется некоторая совокупность объектов, каждому
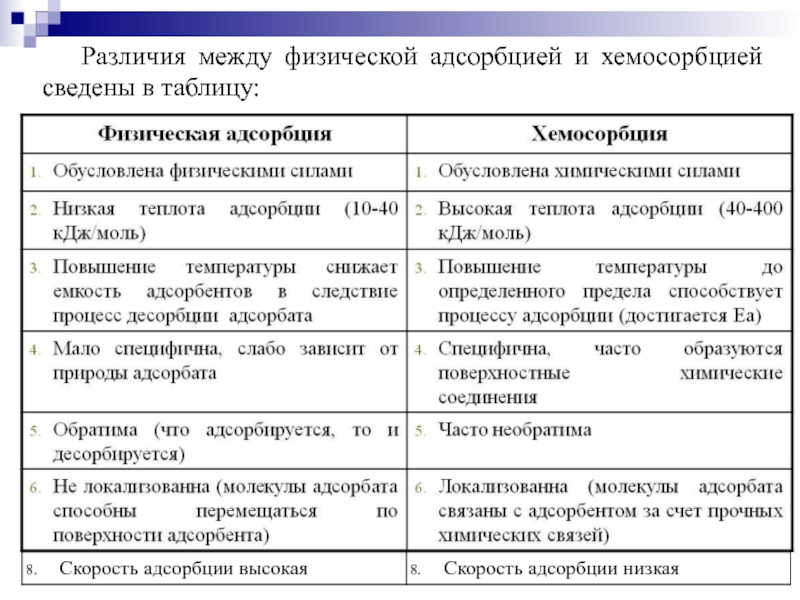
- 15. Различия между физической адсорбцией и хемосорбцией сведены в таблицу:
- 16. Классификация на основе границы раздела твердое тело
- 17. Физическая адсорбция Физическая адсорбция обусловлена на 90
- 18. б) индукционные силы, порожденные взаимодействием диполя с
- 19. Водородная связь, в отличие от сил Ван-дер-Ваальса,
- 20. Химическая адсорбция Хемосорбция - процесс образования поверхностного
- 21. Адсорбция диоксида серы углеродной поверхностью Десорбция Термическая десорбция Экстракционная десорбция
- 22. Термическое уравнение адсорбции Адсорбционный процесс заключается в
- 23. Адсорбционная емкость конкретного адсорбента по отношению к
- 24. Изотермы адсорбции Так как адсорбция - процесс
- 25. Типы изотерм адсорбции согласно С. Брунауэру Изотермы
- 26. Типы изотерм адсорбции согласно С. Брунауэру Изотерма
- 27. Зависимость равновесной величины адсорбции от
- 28. p = f(t) при a = const
- 29. Теплота адсорбции Одновременное использование изотерм и изостер
- 30. Дифференциальной теплотой адсорбции q
- 31. Величину Qad обычно измеряют в результате
- 32. Из точек пресечения изостер
- 34. Адсорбенты Адсорбенты — высокодисперсные природные или искусственные
- 35. Классификация адсорбентов
- 36. Рыночные доли производителей адсорбентов в РФ (по данным 2014 г.)
- 37. Рыночные доли производителей адсорбентов в РФ (по
- 38. Углеродные адсорбенты Углеродными адсорбентами называются углеродсодержащие
- 39. Активные угли Активированные угли – это группа
- 40. По своим структурным характеристикам активные угли относятся к
- 41. Пористая структура Между отдельными частицами углеродного материала
- 42. Пористая структура углеродных адсорбентов представлена макропорами и
- 43. Конфигурация пор активных углей различна. Наряду с
- 44. Линейные размеры пористой структуры адсорбентов и распределение
- 45. Активные угли имеют весьма развитую удельную поверхность,
- 46. Химический состав активных углей АУ
- 47. Фрагмент поверхности окисленного угля Природа поверхности углеродных
- 48. Состав золы активных углей Все активные угли
- 49. Классификация Большое разнообразие адсорбционных процессов и, соответственно,
- 50. Классификация в зависимости от назначения АУ В
- 51. осветляющие (БАУ, ОУ, КАД); предназначены для поглощения
- 52. для приготовления катализаторов, осушителей и химических поглотителей
- 53. Классификация по способу формования экструзионные; брикетированные; жидкостного
- 54. Технология получения углеродных адсорбентов Типовая схема получения
- 55. Сырье Критерии при выборе сырья для производства
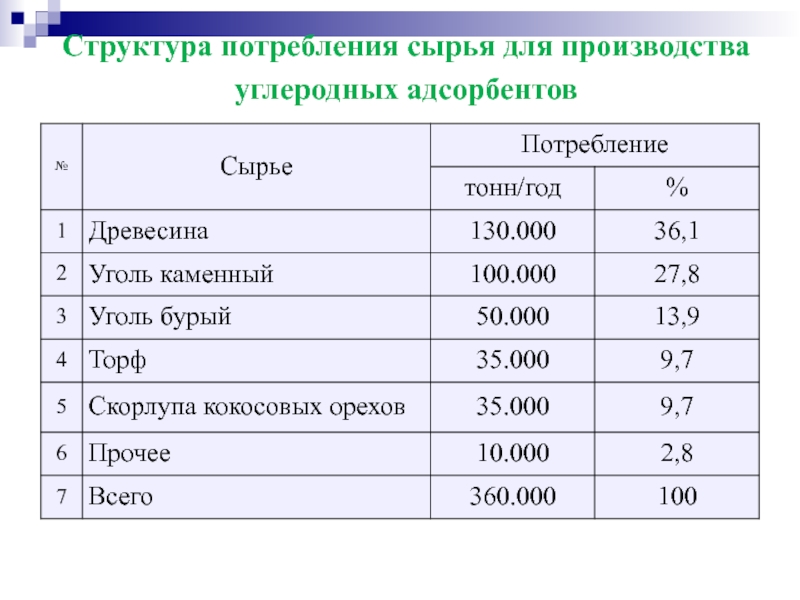
- 56. Структура потребления сырья для производства углеродных адсорбентов
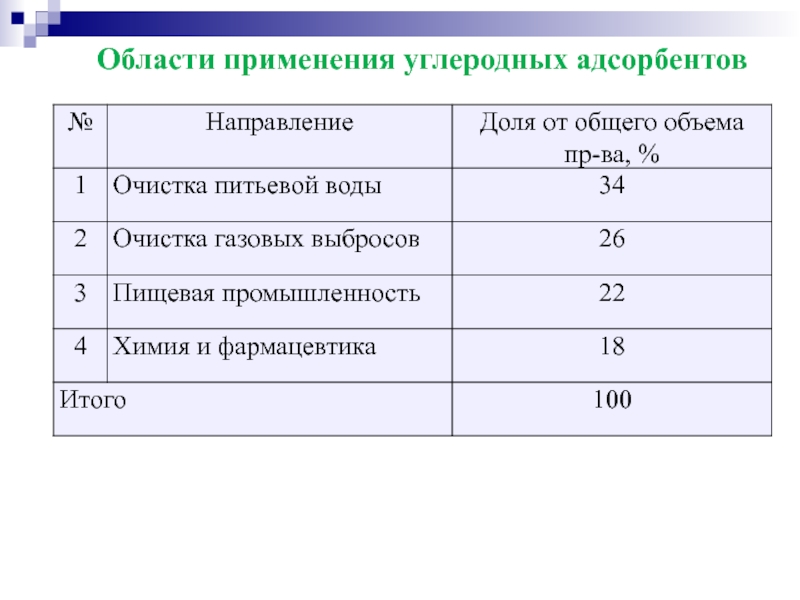
- 57. Области применения углеродных адсорбентов
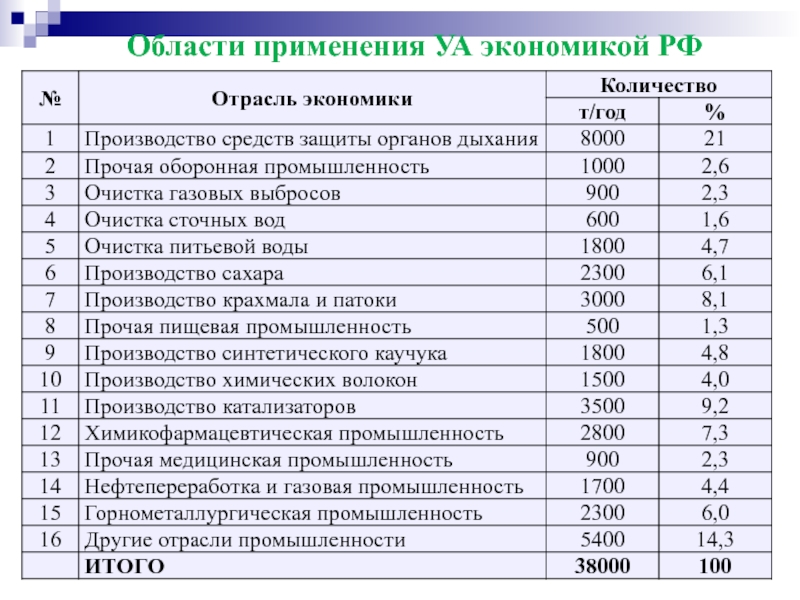
- 58. Области применения УА экономикой РФ
- 59. Минеральные адсорбенты Цеолиты Цеолиты – кристаллические
- 60. Минеральные адсорбенты Цеолиты
- 61. Цеолиты бывают: природные (горные породы); синтетические. То
- 62. Сокирницкое (Украина), Тедзамское и Дзегвское (Грузия), Айдагское
- 63. Холинское, Шивыртуйское и Бадинское (Читинская область), Хонгуруу
- 65. Распределение балансовых запасов цеолитов на территории России
- 66. Текстура и свойства поверхности Цеолиты обладают
- 67. Когда каждый атом кислорода принадлежит двум
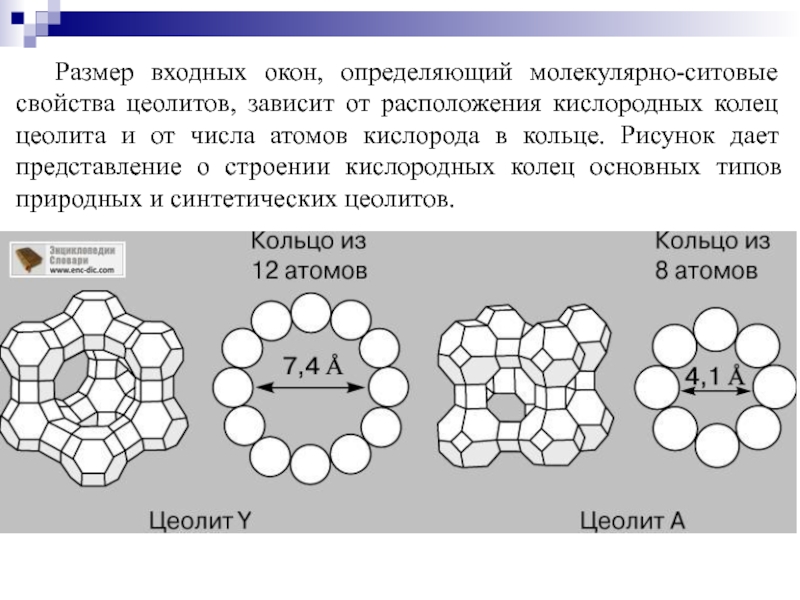
- 68. Размер входных окон, определяющий молекулярно-ситовые свойства цеолитов,
- 69. Поверхность цеолитов гетероионна, т.е. на поверхности кристалла
- 70. Классификация цеолитов В основу классификации, принятой в
- 71. Классификацию цеолитов в соответствии с их молекулярно-ситовым
- 72. Некоторые синтетические цеолиты имеют природные аналоги. Например,
- 73. Цеолиты проявляют избирательность по отношению к различным
- 74. Термостойкость. Большинство промышленно важных типов цеолитов устойчивы
- 75. Силикагели Силикагели – аморфные формы диоксида кремния
- 76. Диаметр глобул обычно составляет 2-3 нм. Зазоры
- 77. На рис. приведены модели двух глобулярных структур,
- 78. Силикагель относится к
- 79. 2.2. Маркировка По характеру пористой структуры
- 80. Иногда в наименовании силикагеля появляется четвертая буква,
- 81. 2.3. Адсорбционные свойства Силикагель обладает высокой адсорбционной способностью,
- 82. 2.4. Регенерация При практическом применении силикагелей большое
- 83. Критерий Пирсона Пусть по выборке объема n
- 84. Правила проверки Для того, чтобы при заданном
- 85. Корреляционно-регрессионный анализ Корреляционная зависимость Корреляционный момент Коррелированность
- 86. Во многих задачах требуется установить или оценить
- 87. Корреляционная зависимость Предположим изучается связь между случайными
- 88. Коэффициент корреляции. Выборочным коэффициентом корреляции называется отношение
- 89. Корреляционный момент Корреляционным моментом μху случайных
- 90. Коррелированность и зависимость случайных величин Две случайных
- 91. Выборочное корреляционное отношение Для оценки тесноты нелинейной
- 92. Достоинства корреляционного отношения. Корреляционное отношение служит мерой
- 93. Простейшие случаи криволинейной корреляции Если график регрессии
- 94. Метод наименьших квадратов Метод наименьших квадратов заключается
- 95. Для того чтобы найти погрешность данного метода
- 96. Если нужно отобрать 20% изготовленных деталей, то
- 97. Задано распределение частот выборки. Определить объем, написать
- 98. Пусть имеется нормальное распределение. Тогда нужно оценить,
- 99. Найти доверительный интервал с надежностью 0.9 неизвестного
- 100. По данным выборки, объема 50, найдена
- 101. При доверительной вероятности 90% найти доверительный интервал
- 102. Если Н0 состоит в предположении, что математическое
- 103. По двум малым независимым выборкам объемов nx=11
Слайд 1АДСОРБЦИОННЫЕ ПРОЦЕССЫ Кафедра технологии неорганических веществ и электрохимических процессов д.т.н., профессор Ануров
Слайд 2СОДЕРЖАНИЕ КУРСА
Введение
Задачи и содержание курса. Роль курса в подготовке инженеров-технологов,
Физико-химические и инженерные основы адсорбционных процессов
Основные понятия в теории адсорбции Адсорбция и силы ее обуславливающие, типы адсорбционных взаимодействий, адсорбционный потенциал на поверхности и в порах адсорбентов.
Слайд 3СОДЕРЖАНИЕ КУРСА
Введение
Задачи и содержание курса. Роль курса в подготовке инженеров-технологов,
Физико-химические основы адсорбционных процессов
Основные понятия в теории адсорбции Адсорбция и силы ее обуславливающие, типы адсорбционных взаимодействий, адсорбционный потенциал на поверхности и в порах адсорбентов.
Слайд 4 Промышленные адсорбенты Характеристики промышленных адсорбентов. Активные угли, силикагели, алюмогели, цеолиты. Структура,
Статика адсорбции
Теплота адсорбции. Теория мономолекулярной адсорбции Ленгмюра. Теория полимолекулярной адсорбции Брунауэра-Эммета-Теллера (БЭТ). Потенциальная теория Поляни. Теория Классификация пор по Дубинину. Теория объемного заполнения микропор. Слабо сорбирующиеся газы. Адсорбция при повышенных давлениях. Адсорбция смесей.
Слайд 5 Кинетика адсорбции Предмет изучения, внешняя диффузия, внутренняя диффузия. Виды переноса в
Тепломассообмен в адсорбционных процессах Теплообмен и массообмен в зернистом слое. Основные модели динамики адсорбции. Сравнительная характеристика равновесных и неравновесных моделей фронтальной изотермической и неизотермической адсорбции.
Слайд 6Технология и расчет адсорбционных процессов
Основные этапы развития адсорбционных процессов, классификация адсорбционных
Процессы с однократным использованием адсорбента.
Процессы с многократным использованием адсорбента.
Процессы с реактивацией адсорбента.
Процессы TSA (Thermal (Temperature) Swing Adsorption) с термопродувочной и термовытеснительной регенерацией адсорбента.
Циклические процессы
Принципы построения циклограмм, организация процессов, подбор адсорбентов.
Слайд 7Процессы осушки Технология процесса, адсорбенты-осушители, основное оборудование. Расчет и анализ материальных и
Рекуперация углеводородов
Особенности технологии и аппаратуры процессов. Принципы проектирования установок.
Процессы PSA (Pressure Swing Adsorption)
очистка воздуха
очистка водорода
адсорбционное разделение воздуха
очистка от диоксида углерода
получение защитных атмосфер
Очистка от соединений серы
Слайд 8
Основные понятия и определения
Адсорбция – процесс самопроизвольного перераспределения компонентов системы между
На любой границе раздела существует «поверхностный слой» – переходная область от одной объемной фазы к другой. Поверхностный слой имеет очень малую толщину (всего несколько молекул), но в ней сосредоточен весь избыток поверхностной энергии.
Атомы (или молекулы), примыкающие к поверхности, ограничивающей конденсированную фазу, отличаются от расположенных в объеме той же фазы отсутствием части соседей и, соответственно, не полной скомпенсированностью межатомных или межмолекулярных связей.
Особое состояние таких атомов характеризуется величиной избыточной поверхностной энергией, которая проявляется во многих явлениях, называемых поверхностными явлениями.
Слайд 9
В однокомпонентных системах при формировании поверхностного слоя происходит изменение
В многокомпонентных системах в поверхностный слой предпочтительнее переходит тот компонент, который сильнее уменьшает межфазное (поверхностное) натяжение.
Движущей силой адсорбции является стремление системы уменьшить свою поверхностную энергию за счет уменьшения поверхностного натяжения:
где - поверхностная энергия, равная средней энергии частицы, находящейся на поверхности раздела фаз и средней энергии частицы, находящейся в объеме фазы;
- отношение поверхностной энергии в к площади поверхности раздела фаз;
S - величина поверхности раздела фаз
Слайд 10Основные определения
Адсорбция - поглощение частиц какого-либо вещества поверхностью поглотителя, приводящее к
Адсорбция – поглощение твёрдой поверхностью газов, паров или жидкостей
С термодинамической точки зрения адсорбция – самопроизвольный процесс выравнивания химических потенциалов в объеме системы и поверхностном слое.
Слово адсорбция образовано из латинского слова sorbeo – поглощение и приставки ad – т.е. над или у и означает поглощение (точнее – концентрирование ) каких либо компонентов из объема гомогенных сопредельных фаз на границе (поверхности) раздела этих фаз.
Слайд 11
Обычно рассматривают адсорбцию компонентов газообразной или жидкой среды (в общем
Введем еще несколько терминов, предложенных Международным союзом чистой и прикладной химии (IUPAC):
Адсорбент – твёрдое тело, на поверхности которого происходит процесс поглощения
Адсорбтив – поглощаемое вещество, находящееся в объёме фазы
Адсорбат – адсорбированное (поглощённое) вещество, находящееся на поверхности (в порах) адсорбента
(т.е. адсорбтив адсорбируется на адсорбенте, превращаясь в адсорбат)
Десорбция – процесс, обратный адсорбции
Слайд 12 Сорбция, сорбент, сорбат, сорбтив – термины применяют, когда механизм поглощения
Объемная фаза (синонимы: поток, среда) – среда, подвергаемая очистке (разделению). Она представляет собой жидкость или газ.
Подвергаемая очистке объемная фаза представляет собой смесь компонентов, один (одни) из которых поглощается лучше, чем другой (другие). Различия в адсорбируемости компонентов вытекают из различий в свойствах, строении и структуре молекул объемной фазы, взаимодействующих с адсорбентом. Свое проявление эти различия находят в адсорбционной емкости (синонимы: адсорбционная активность, величина адсорбции, концентрация адсорбата в адсорбенте), которая характеризует способность единичной массы (объема) адсорбента поглощать компоненты очищаемой среды.
Слайд 13
Пусть исследуется некоторая совокупность объектов, каждому из которых ставится в соответствие
Размерность адсорбционной емкости поглотителей
Адсорбционную активность выражают в виде:
числа молей адсорбата, поглощаемых 1 г адсорбента, моль/г;
см3 (мл)/г;
г/100 г;
мг/г;
г/м3;
% массовые.
Слайд 14
Пусть исследуется некоторая совокупность объектов, каждому из которых ставится в соответствие
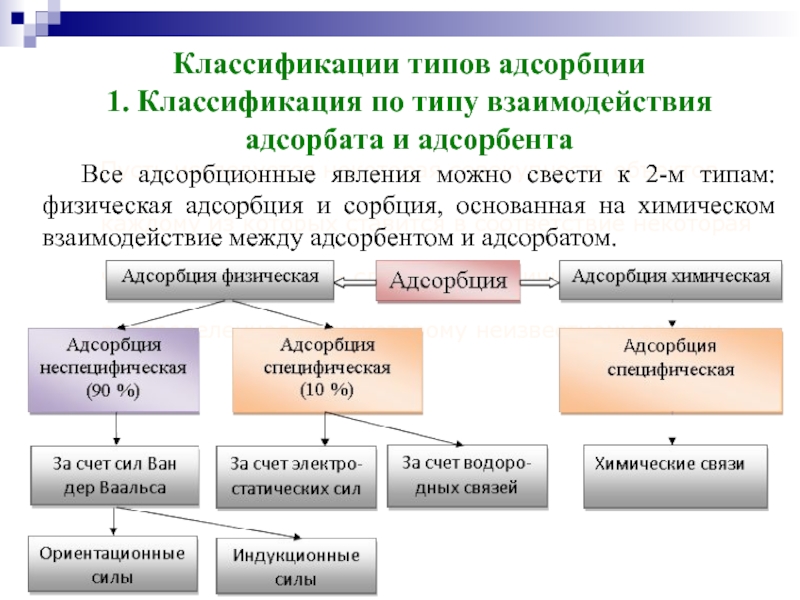
Классификации типов адсорбции
1. Классификация по типу взаимодействия адсорбата и адсорбента
Все адсорбционные явления можно свести к 2-м типам: физическая адсорбция и сорбция, основанная на химическом взаимодействие между адсорбентом и адсорбатом.
Слайд 16Классификация на основе границы раздела
твердое тело – газ.
жидкость - газ.
твердое тело
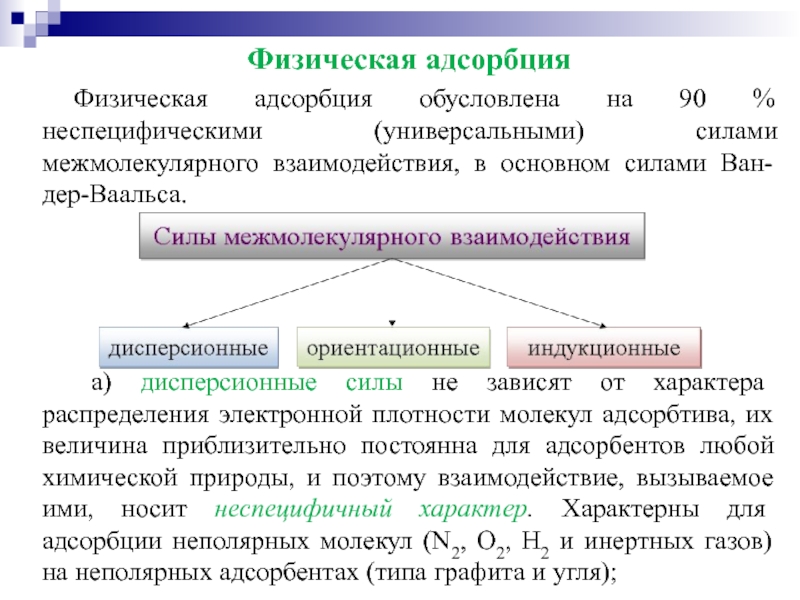
Слайд 17Физическая адсорбция
Физическая адсорбция обусловлена на 90 % неспецифическими (универсальными) силами межмолекулярного
а) дисперсионные силы не зависят от характера распределения электронной плотности молекул адсорбтива, их величина приблизительно постоянна для адсорбентов любой химической природы, и поэтому взаимодействие, вызываемое ими, носит неспецифичный характер. Характерны для адсорбции неполярных молекул (N2, О2, Н2 и инертных газов) на неполярных адсорбентах (типа графита и угля);
Слайд 18б) индукционные силы, порожденные взаимодействием диполя с другим наведенным им диполем,
в) ориентационные силы, порожденные взаимной ориентацией взаимодействующих диполей, - характерны для адсорбции полярных молекул (Н2О, СО2, NH3 и др.) на полярных адсорбентах с ионной связью (типа SiO2 , и др.).
Кроме диполь-дипольных, в физической адсорбции участвуют ион-дипольные и квадрупольные взаимодействия.
Электростатическое взаимодействие зависит от химической природы адсорбента и адсорбтива и является специфическим.
Слайд 19Водородная связь, в отличие от сил Ван-дер-Ваальса, является специфической, т.е. локальной,
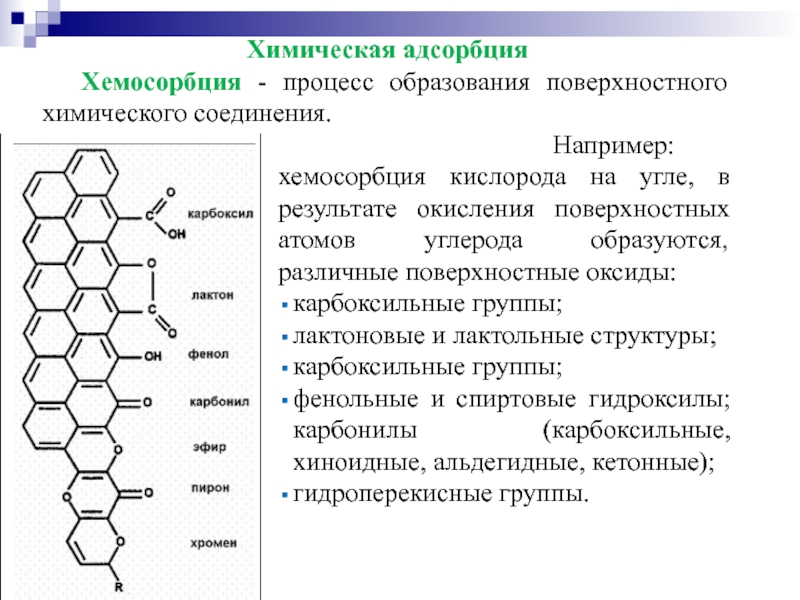
Слайд 20Химическая адсорбция
Хемосорбция - процесс образования поверхностного химического соединения.
Например: хемосорбция кислорода
карбоксильные группы;
лактоновые и лактольные структуры;
карбоксильные группы;
фенольные и спиртовые гидроксилы; карбонилы (карбоксильные, хиноидные, альдегидные, кетонные);
гидроперекисные группы.
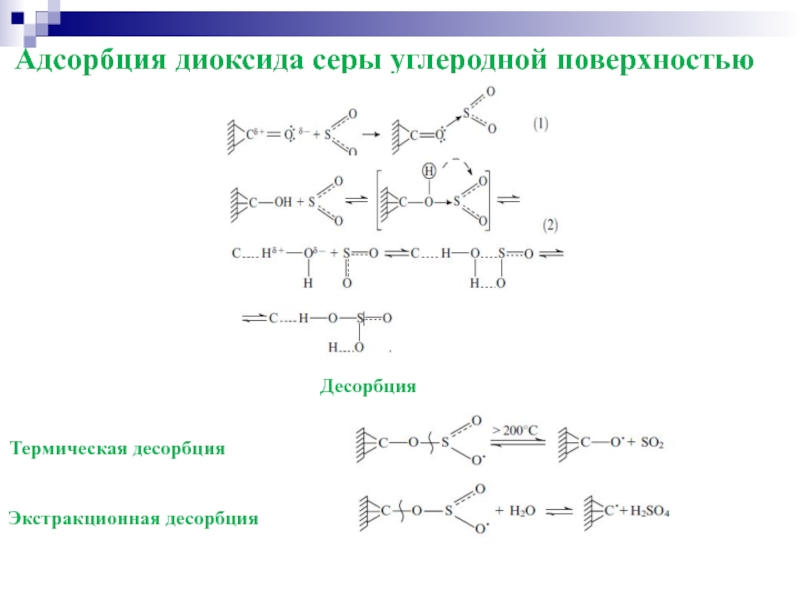
Слайд 21Адсорбция диоксида серы углеродной поверхностью
Десорбция
Термическая десорбция
Экстракционная десорбция
Слайд 22Термическое уравнение адсорбции
Адсорбционный процесс заключается в приведении в контакт объемной фазы,
Отношение величины адсорбции целевого компонента (а или А) к его концентрации в объемной фазе (С):
К = а/С
называется коэффициентом распределения адсорбата.
В системах адсорбент - адсорбат коэффициент распределения зависит от типа системы и условий, в которых она находиться; он лежит в пределах 101 - 106 и выше. Отношение коэффициентов распределения двух адсорбатов, находящихся в смеси, называют коэффициентом разделения.
Слайд 23Адсорбционная емкость конкретного адсорбента по отношению к поглощаемому веществу зависит от
а = (p, t)
Это уравнение называется термическим уравнением адсорбции.
На практике сравнительная оценка адсорбционных свойств твердых поглотителей по конкретным компонентам осуществляется по их адсорбционная емкость в зависимости от концентрации адсорбата в объемной фазе при постоянной температуре, т.е.:
a = f (C) при t = const
Это уравнение называется изотермой адсорбции.
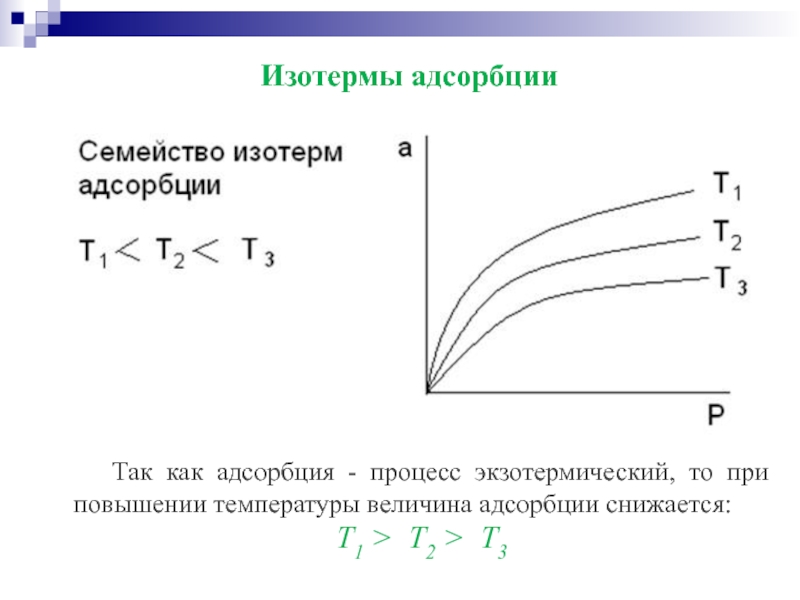
Слайд 24Изотермы адсорбции
Так как адсорбция - процесс экзотермический, то при повышении температуры
Т1 > Т2 > Т3
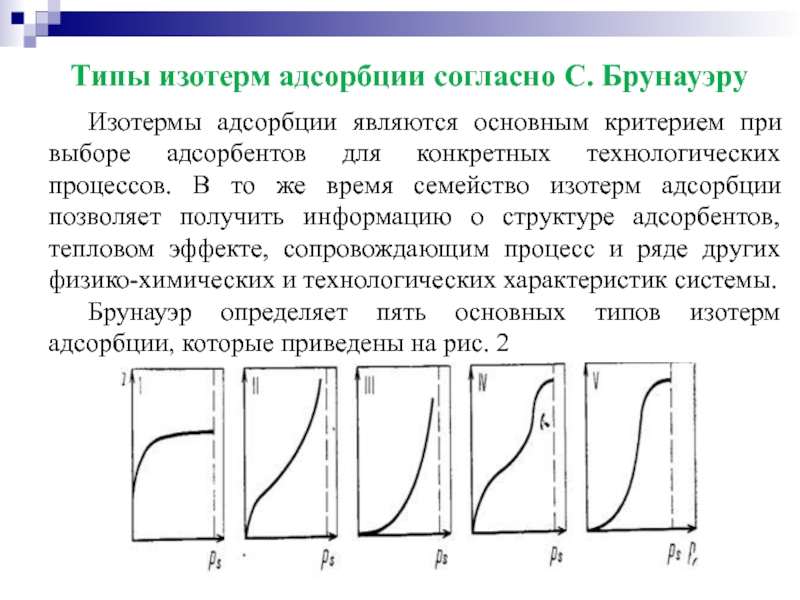
Слайд 25Типы изотерм адсорбции согласно С. Брунауэру
Изотермы адсорбции являются основным критерием при
Брунауэр определяет пять основных типов изотерм адсорбции, которые приведены на рис. 2
Слайд 26Типы изотерм адсорбции согласно С. Брунауэру
Изотерма типа I отражает мономолекулярную адсорбцию
Слайд 27
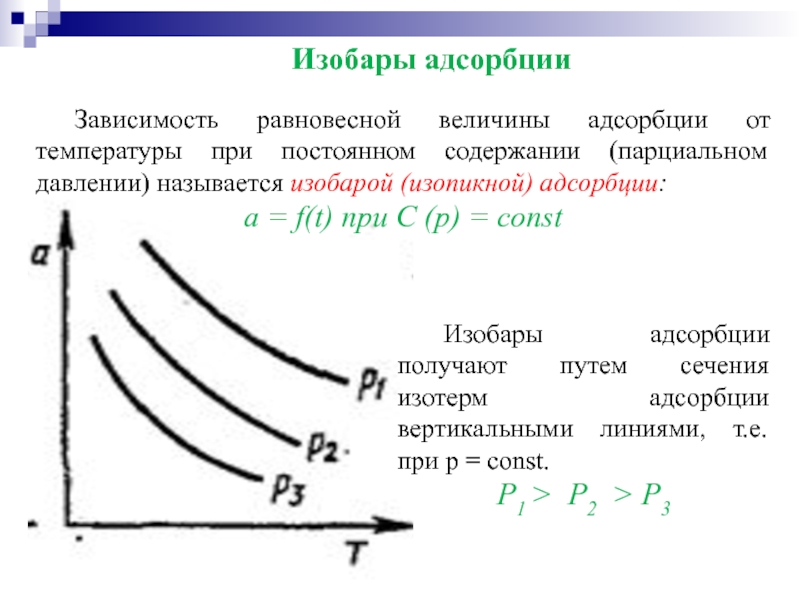
Зависимость равновесной величины адсорбции от температуры при постоянном содержании (парциальном давлении)
a = f(t) при C (p) = const
Изобары адсорбции получают путем сечения изотерм адсорбции вертикальными линиями, т.е. при р = const.
Р1 > Р2 > Р3
Изобары адсорбции
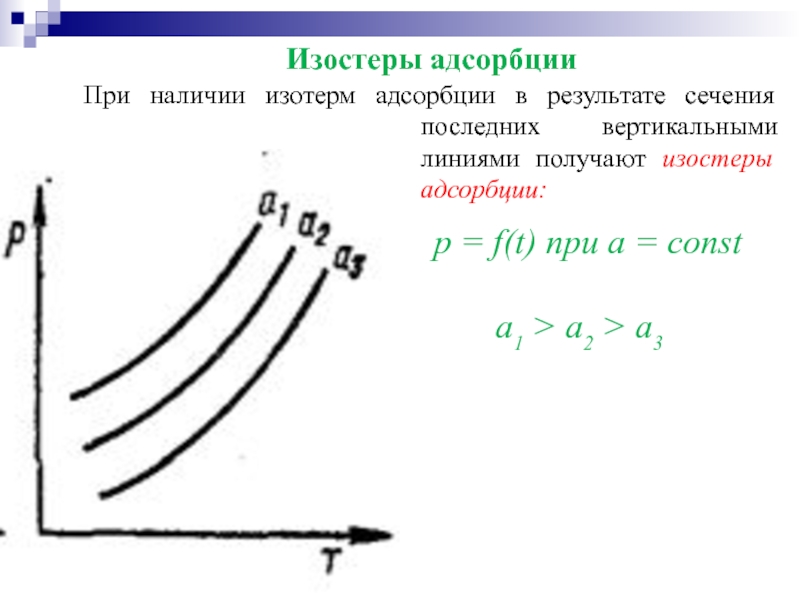
Слайд 28p = f(t) при a = const
а1 > а2 > а3
Изостеры адсорбции
При наличии изотерм адсорбции в результате сечения последних вертикальными линиями получают изостеры адсорбции:
Слайд 29Теплота адсорбции
Одновременное использование изотерм и изостер адсорбции позволяет определить два важнейших
Различают два основных понятия:
интегральная теплота адсорбции;
дифференциальная теплота адсорбции.
Интегральной теплотой адсорбции Q называется полное количество теплоты, выделяющейся при адсорбции n молей адсорбата. Ее относят к единице массы адсорбента (Дж/кг):
qинт = Q/m
Слайд 30
Дифференциальной теплотой адсорбции q называют отнесенное к 1 моль адсорбата дополнительное
Пусть на поверхности адсорбента адсорбировалось n молей адсорбата и выделилось Q калорий тепла. Затем адсорбировалось еще dn молей адсорбата с тепловым эффектом dQ. Дифференциальной теплотой адсорбции называется тепло, выделившееся при дополнительной адсорбции малого количества адсорбата и пересчитанное на один его моль.
qдиф = dQ/dn
Слайд 31
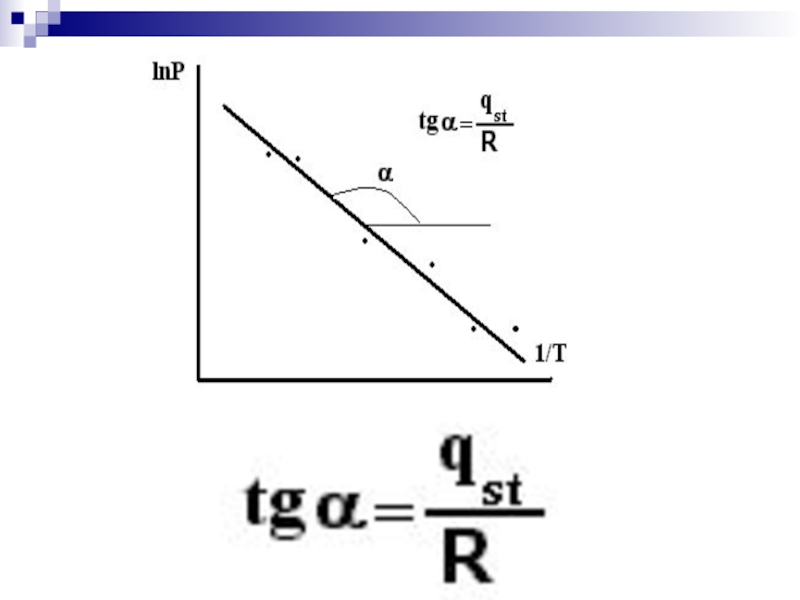
Величину Qad обычно измеряют в результате прямых экспериментов в калориметрах.
Значение qst
а = f(P) проводят ряд линий - изостер при а = const (линии параллельные оси абсцисс).
На рис.1.2 а приведены изостеры адсорбции в координатах а ~ T. На рис.1.2 б эти же изостеры представлены в координатах линейной формы уравнения Клапейрона-Клаузиуса:
ln а = - ΔqRT
Изотермы адсорбции
Слайд 32
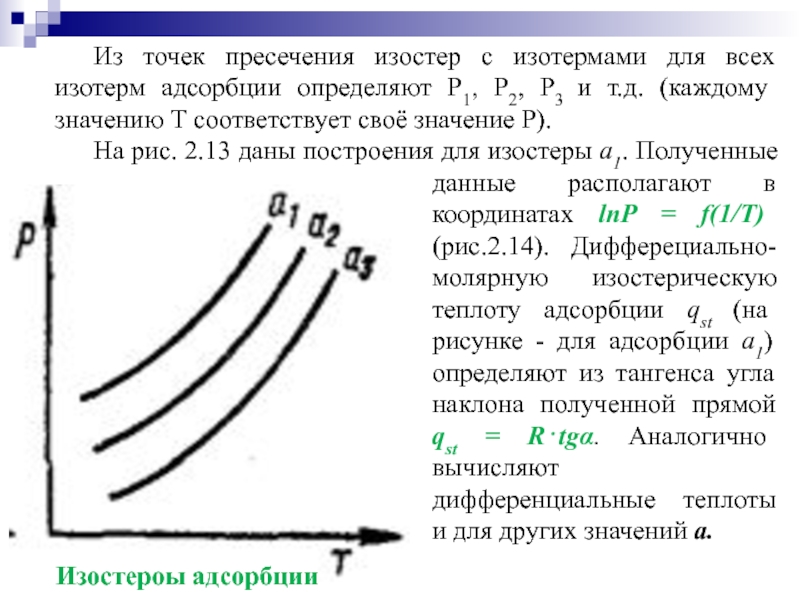
Из точек пресечения изостер с изотермами для всех изотерм адсорбции определяют
На рис. 2.13 даны построения для изостеры a1. Полученные данные располагают в координатах lnP = f(1/Т) (рис.2.14). Дифферециально-молярную изостерическую теплоту адсорбции qst (на рисунке - для адсорбции a1) определяют из тангенса угла наклона полученной прямой qst = R⋅tgα. Аналогично вычисляют дифференциальные теплоты и для других значений a.
Изоcтероы адсорбции
Слайд 34Адсорбенты
Адсорбенты — высокодисперсные природные или искусственные материалы с большой удельной поверхностью,
химического состава и физического состояния поверхности;
характера пористости;
удельной поверхности.
Все промышленные адсорбенты в зависимости от их химического состава можно подразделить на 3 класса:
углеродные;
минеральные;
полимерные.
В каждом классе имеются собственные подклассы.
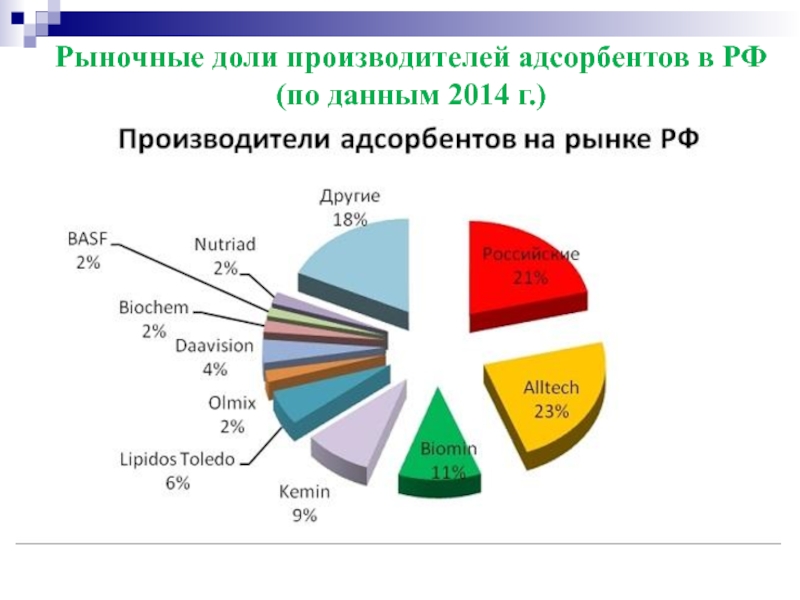
Слайд 37Рыночные доли производителей адсорбентов в РФ (по данным 2014 г.)
Сегодня на
Слайд 38Углеродные адсорбенты
Углеродными адсорбентами называются углеродсодержащие материалы, получаемые на основе природного или
Среди них наибольшее значение имеют активные (активированные) угли.
Слайд 39Активные угли
Активированные угли – это группа углеродных сорбентов, (зерненые, порошкообразные, гранулированные)
1. зерненный (дробленый) 2. порошкообразный 3. гранулированный
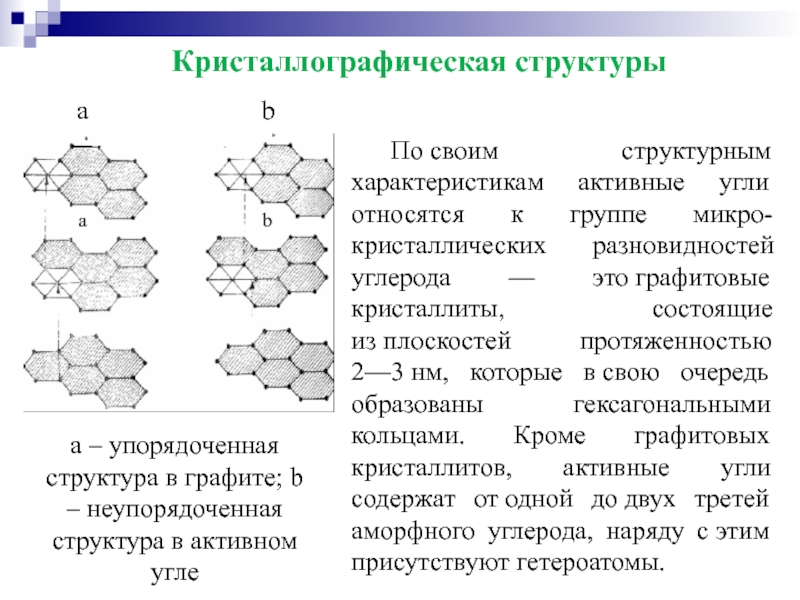
Слайд 40По своим структурным характеристикам активные угли относятся к группе микро-кристаллических разновидностей углерода
а – упорядоченная структура в графите; b – неупорядоченная структура в активном угле
a b
Кристаллографическая структуры
a b
Слайд 41Пористая структура
Между отдельными частицами углеродного материала имеются поры шириной 10-10-10-8 м. Эти
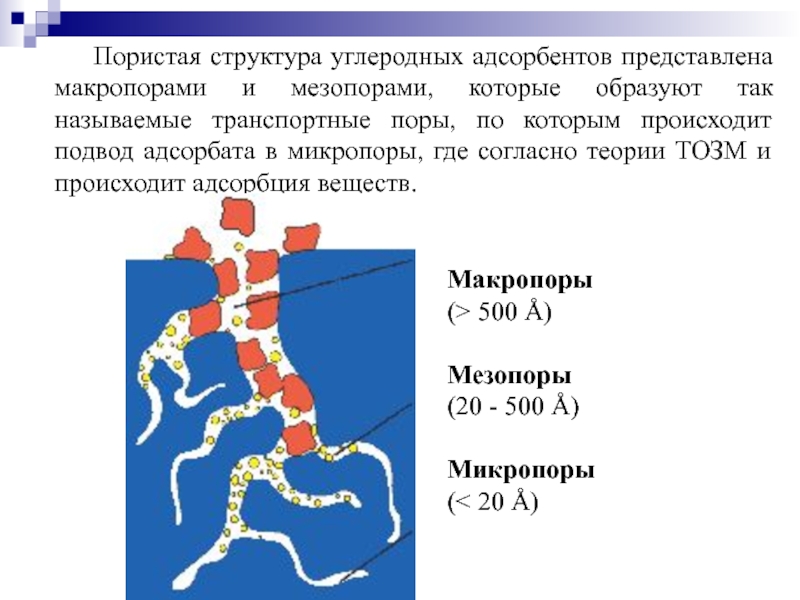
Слайд 42Пористая структура углеродных адсорбентов представлена макропорами и мезопорами, которые образуют так
Макропоры
(> 500 Å)
Мезопоры
(20 - 500 Å)
Микропоры
(< 20 Å)
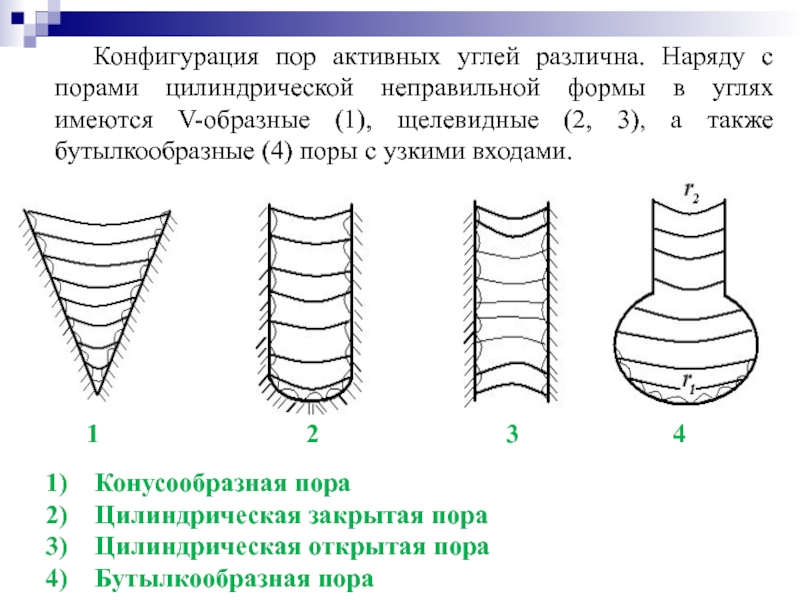
Слайд 43Конфигурация пор активных углей различна. Наряду с порами цилиндрической неправильной формы
Конусообразная пора
Цилиндрическая закрытая пора
Цилиндрическая открытая пора
Бутылкообразная пора
1 2 3 4
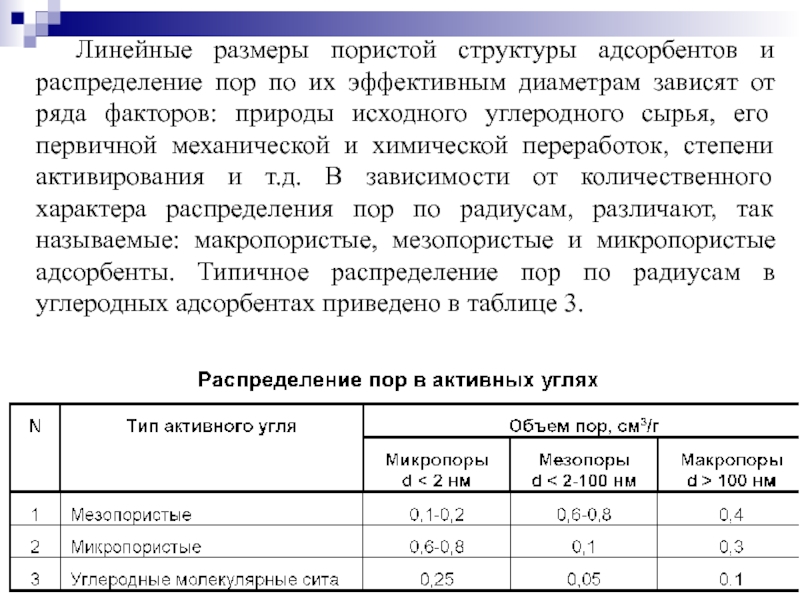
Слайд 44Линейные размеры пористой структуры адсорбентов и распределение пор по их эффективным
Слайд 45Активные угли имеют весьма развитую удельную поверхность, которая достигает 500-3000 м2/г. Столь
Слайд 46
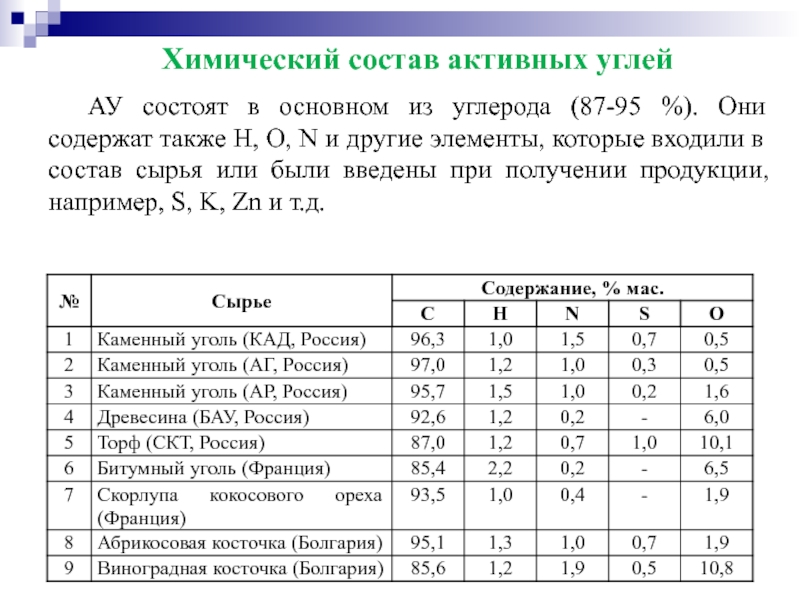
Химический состав активных углей
АУ состоят в основном из углерода (87-95 %).
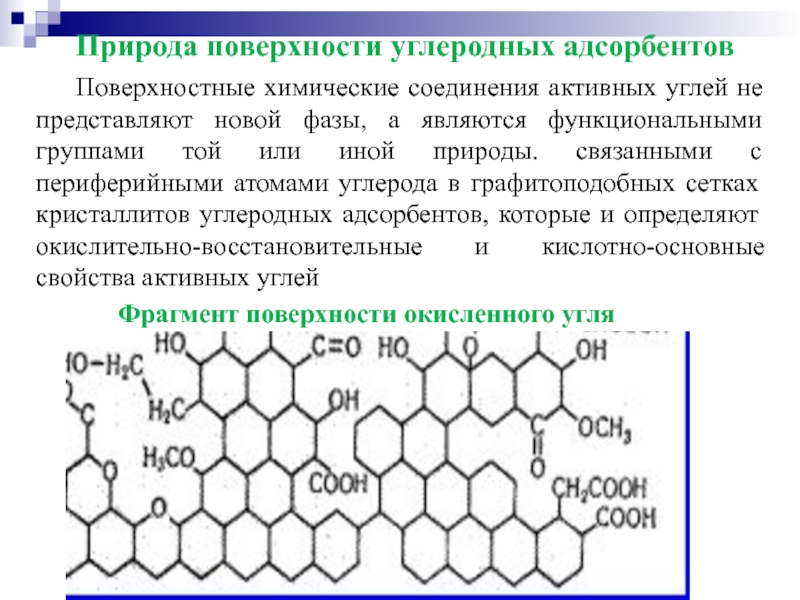
Слайд 47Фрагмент поверхности окисленного угля
Природа поверхности углеродных адсорбентов
Поверхностные химические соединения активных углей
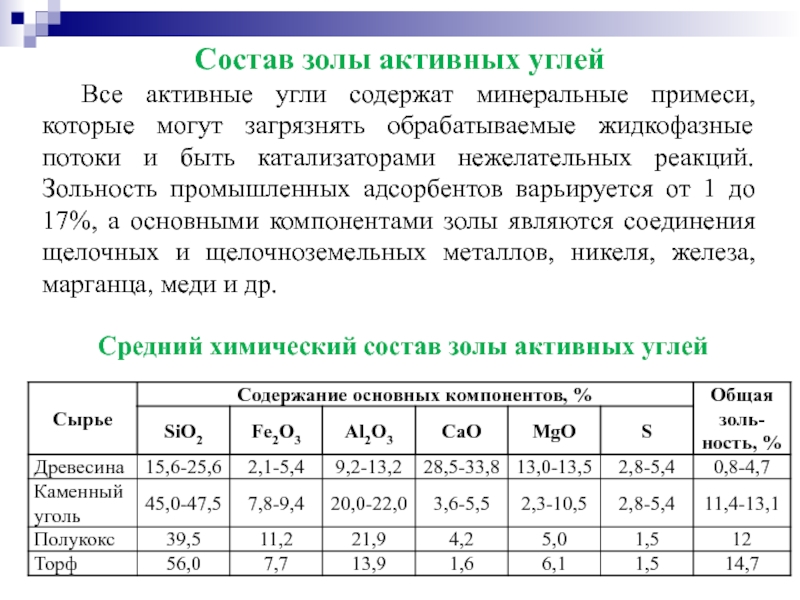
Слайд 48Состав золы активных углей
Все активные угли содержат минеральные примеси, которые могут
Средний химический состав золы активных углей
Слайд 49Классификация
Большое разнообразие адсорбционных процессов и, соответственно, требований к активным углям привело
Классификация по форме частиц
гранулированные; форма гранул может быть цилиндрической и сферической. Эти активные угли используются на установках со стационарным слоем для очистки и разделения газовых и жидкофазных потоков;
дробленые; зернистая неправильная форма, используются во всех вариантах адсорбционных процессов (со стационарным, движущимся, псевдоожиженным слоем адсорбента);
порошковые; пылевидные частицы размером < 100 мкм, используются для очистки веществ в жидкой фазе.
Слайд 50Классификация в зависимости от назначения АУ
В этой классификации каждый тип угля
газовые (СКТ); предназначены для улавливания примесей, присутствующих в газовых потоках в небольших концентрациях. Эти угли должны обладать большим объемом микропор (не менее 0,3-0,5 см3/г) и умеренно развитой транспортной пористостью (≥ 0,1 см3/г), обеспечивающей достаточную интенсивность диффузии внутри зерна адсорбента;
рекуперационные (АРТ). Их назначение – улавливание паров органических растворителей с последующей их десорбцией и возвратом растворителей в технологический процесс. Так как стадия десорбции должна проводиться без осложнений, суммарный объем макро- и мезопор рекуперационных углей должен быть примерно равным объему микропор;
Слайд 51осветляющие (БАУ, ОУ, КАД); предназначены для поглощения веществ из жидких сред,
для очистки почв (Агросорб); предназначены для детоксикации почв, загрязненных пестицидами; для устранения из почвы тяжелых металлов, радионуклидов с одновременным кондиционированием почв. Эти угли должны обладать объемом микропор ~ 0,2-0,3 см3/г) и развитой транспортной ористостью;
медицинские (ФАС-Э, СКТ-6А); предназначены для поглощения вредных веществ из желудочно-кишечного тракта, крови, плазмы и лимфы. Эти угли должны обладать большими объемами микропор (не менее 0,4-0,5 см3/г) и транспортных пор (не менее 0,4 см3/г). Помимо высокой пористости эти угли должны обладать высокой механической прочностью;
Слайд 52для приготовления катализаторов, осушителей и химических поглотителей (ОЛБ, ОЛ, КГ); используются
Классификация по форме частиц
каменноугольные;
торфяные;
древесные;
косточковые;
полимерные;
из отходного сырья.
Классификация по способу активации
парогазовой активации;
химической активации;
смешанная.
Слайд 53Классификация по способу формования
экструзионные;
брикетированные;
жидкостного формования.
Классификация по прочностным свойствам
низкопрочные;
высокопрочные.
Классификация по показателю насыпной
с низкой плотностью (< 300 г/л);
с нормальной плотностью (300 – 500 г/л));
с высокой плотностью (> 500 г/л).
Реактивированные АУ – это отработанные угли с восстановленными адсорбционными свойствами для повторного использования (АР-Р, АГ-Р).
Определяющими техническими характеристиками АУ являются адсорбционная способность, прочность при истирании, насыпная плотность, фракционный состав и содержание золы.
Слайд 54Технология получения углеродных адсорбентов
Типовая схема получения углеродных адсорбентов включает следующие стадии:
подготовка
карбонизация углеродсодержащего сырья - термообработка обычно без доступа окислителя при 500 - 900 оС;
активации карбонизата.
Активация углеродных матриц бывает:
физической (парогазовой) в присутствии окислителя (пары воды, СО2, воздух либо их смесь) при 700-1000 оС.
химической в результате введения в исходный материал неорганических катализаторов (ZnCl2, H3PO4, карбонаты калия и др.) с карбонизацией в инертной среде или в присутствии газообразного окислителяв диапазоне температур 200-850 оС.
Слайд 55Сырье
Критерии при выборе сырья для производства углеродных адсорбентов:
содержание углерода и минеральных
прочность;
количество летучих соединений;
величина запасов;
объемы и легкость добычи сырья;
транспорта и хранения;
затраты на организацию технологического процесса переработки;
экологическая безопасность технологии и т.п.
Слайд 59Минеральные адсорбенты
Цеолиты
Цеолиты – кристаллические водные алюмосиликаты каркасной структуры, из которых путем
где Ме – катион щелочного или щелочноземельного металла с валентностью n (обычно это Na+, K+, Ca2+, Ba2+, Si2+, Mg2+), y – число молекул воды, а отношение у/х может изменяться от 1 до 5 для различных видов цеолитов. Значение х ≥ 2.
Соотношение Na/Al в цеолитах равно 1.
Соотношение SiO2/Al2O3 носит название кремнеземового модуля адсорбента.
Слайд 61Цеолиты бывают:
природные (горные породы);
синтетические.
То есть цеолиты встречаются в природе и известны
Синтетические цеолиты более пригодны для промышленных целей из-за высокой однородности структуры и чистоты, чем природные цеолиты. Однако они на много дороже горных пород.
Природные цеолиты
Основные разведанные запасы природных цеолитов сосредоточены в Европе, России, Японии и США.
Объем разведанных запасов природных цеолитов в странах СНГ составляет порядка 1,6 млрд. т.
К наиболее крупным и целесообразным с точки зрения разработки месторождениям стран СНГ можно отнести:
Слайд 62Сокирницкое (Украина),
Тедзамское и Дзегвское (Грузия),
Айдагское (Азербайджан),
Ноемберянское (Армения),
Тайжузгенское и Чанканайское (Казахстан).
На территории
Хотынецкое (Орловская область),
Татарско-Шатрашанское (Татарстан),
Пегасское (Кемеровская область),
Сахаптинское и Пашенское (Красноярский край),
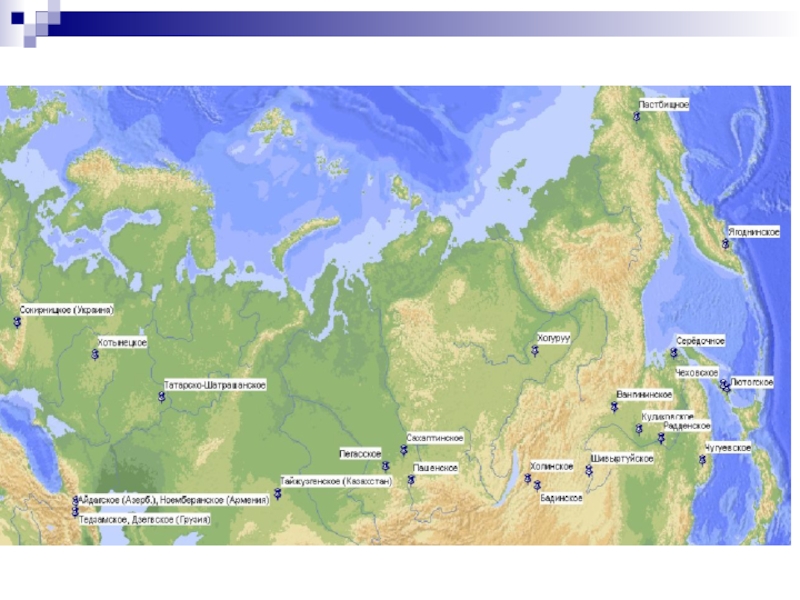
Слайд 63Холинское, Шивыртуйское и Бадинское (Читинская область), Хонгуруу (Республика Саха),
Куликовское и Вангинское
Радденское, Середочное (Хабаровский край),
Чугуевское (Приморский край),
Лютогское и Чеховское (Сахалинская область),
Пастбищное (Чукотский АО).
Ягоднинское (Камчатская область) (рис. 1)
Основную массу сырья данных месторождений составляют клиноптилолитовые породы.
Слайд 65Распределение балансовых запасов цеолитов на территории России
Забайкальский край 72,2
Республика Татарстан 13,3
Приморский
Хабаровский край 3,1
Амурская область 2,3
Республика Саха (Якутия) 1,7
Сахалинская область 1,3
Камчатская область 1,1
Чукотский АО 1,0
Кемеровская область 0,9
Всего 100
Слайд 66Текстура и свойства поверхности
Цеолиты обладают строго регулярной кристаллической структурой. Каркас
Слайд 67
Когда каждый атом кислорода принадлежит двум соседним кремний-кислородным или алюмокислородным тетраэдрам,
Координационные числа у Al и Si равны 4, в вершинах обязательно 4 связи. Al и Si – взаимозаменяющие элементы, но Al имеет валентность 3, а Si – 4, поэтому тетраэдр [AlO4]− имеет отрицательный заряд. Для компенсации в структуру должен быть введен однозарядный катион на одну связь алюминия. Поэтому в цеолитах содержание алюминия равно содержанию натрия.
Цеолиты имеют жесткую упорядоченную трехмерную кристаллическую решетку. Полости сообщаются между собой в трех измерениях. Катионы и молекулы воды не входят в кристаллическую решетку цеолитов, а располагаются в полостях и каналах цеолитов. Распределение электронов в структуре цеолита таково, что имеются определенные предпочтительные места локализации катионов, т.е. места с минимумом энергии..
Слайд 68Размер входных окон, определяющий молекулярно-ситовые свойства цеолитов, зависит от расположения кислородных
Слайд 69Поверхность цеолитов гетероионна, т.е. на поверхности кристалла цеолита имеются отрицательно (ионы
Соотношение SiO2/Al2O3 называется кремневым модулем и определяет кислотостойкость цеолита. Чем выше содержание кремния, тем выше его кислотостойкость.
Катионы не входят в кристаллическую решетку цеолитов и имеют возможность перемещаться со своих основных позиций, мигрировать.
Слайд 70Классификация цеолитов
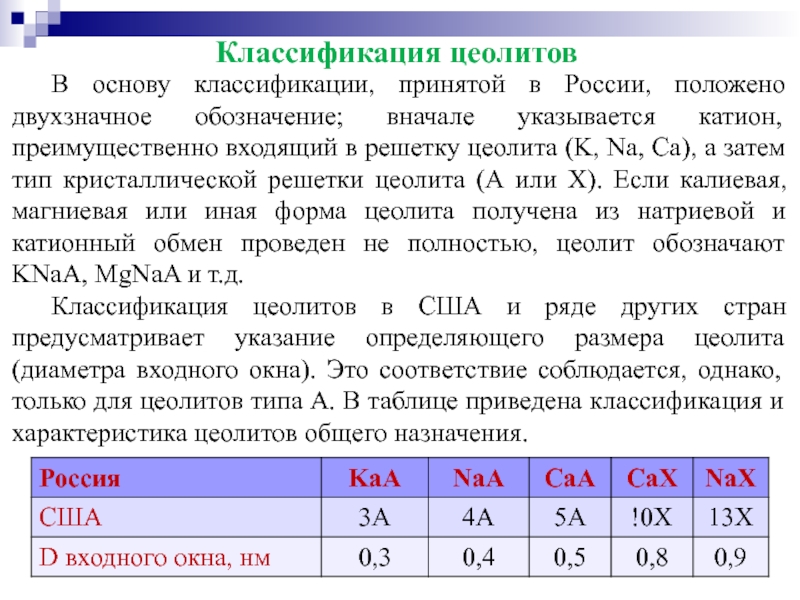
В основу классификации, принятой в России, положено двухзначное обозначение; вначале
Классификация цеолитов в США и ряде других стран предусматривает указание определяющего размера цеолита (диаметра входного окна). Это соответствие соблюдается, однако, только для цеолитов типа А. В таблице приведена классификация и характеристика цеолитов общего назначения.
Слайд 71Классификацию цеолитов в соответствии с их молекулярно-ситовым действием можно представить следующим
Слайд 72Некоторые синтетические цеолиты имеют природные аналоги. Например, природным аналогом цеолитов типа
Слайд 73Цеолиты проявляют избирательность по отношению к различным молекулам, причем молекулярно-ситовое действие
Размер входного окна в цеолит СаА составляет 0,5 нм, он достаточен, чтобы пропустить линейные углеводороды, но он мал, чтобы пропустить разветвленные и циклические изомеры.
Слайд 74Термостойкость. Большинство промышленно важных типов цеолитов устойчивы до 700 оС. Термостабильность
Кислотостойкость. Чем выше соотношение SiO2/Al2O3, тем более кислотоустойчивый и термостабильный цеолит. Среди кислотоустойчивых типов цеолитов следует назвать морденит, шабазит, NaY, силикалит.
Ионообменные свойства. В цеолите, заполненном водой, катионы очень подвижны и, поэтому, способны к ионному обмену. Цеолиты − одни из самых популярных неорганических ионообменников.
Цеолиты обладают каталитическими свойствами. Они содержат кислотные бренстедовские (протоны, связанные с каркасными атомами О) и льюисовские центры (катионы щелочных металлов или трех-координированные атомы алюминия, находящиеся в местах с дефицитом кислорода или местах расположения катионов).
Слайд 75Силикагели
Силикагели – аморфные формы диоксида кремния (содержащие 85-95 % SiO2), состоящие
Промышленный силикагель – ксерогель кремниевой кислоты. Он представляет собой полупрозрачные зерна белого или желтоватого (из-за содержания примесей) цвета.
2.1. Текстура и свойства поверхности
Согласно современным взглядам скелет силикагеля образован сферическими частицами, сросшимися в местах их контактов. При таком строении силикагеля поры представляют собой систему пустот и каналов между различным образом упакованными частицами. Размер частиц определяет величину удельной поверхности, плотность упаковки – объем и радиус пор.
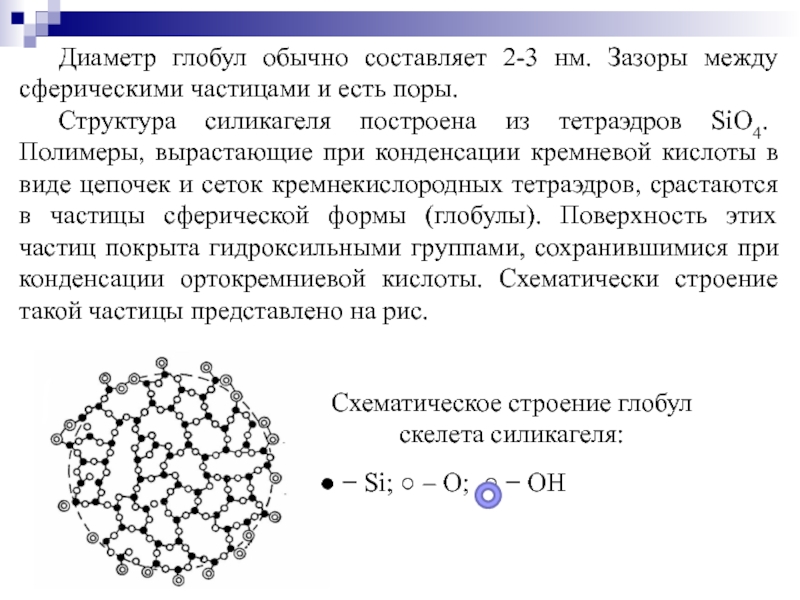
Слайд 76Диаметр глобул обычно составляет 2-3 нм. Зазоры между сферическими частицами и
Структура силикагеля построена из тетраэдров SiO4. Полимеры, вырастающие при конденсации кремневой кислоты в виде цепочек и сеток кремнекислородных тетраэдров, срастаются в частицы сферической формы (глобулы). Поверхность этих частиц покрыта гидроксильными группами, сохранившимися при конденсации ортокремниевой кислоты. Схематически строение такой частицы представлено на рис.
Схематическое строение глобул скелета силикагеля:
● − Si; ○ – O; ○ − OH
Слайд 77На рис. приведены модели двух глобулярных структур, отвечающих мелкопористому и крупнопористому
Для силикагелей характерны большие величины удельной поверхности (5-800 м2/г) и суммарного объма пор (VΣ =0,3-1,2 см3/г).
Модели глобулярной структуры мелкопористого (а) и крупнопористого (б) силикагелей
Слайд 78
Силикагель относится к мезопористым (преимущественный радиус пор от 2 до 50
Для силикагелей характерны большие величины удельной поверхности (5-800 м2/г) и суммарного объёма пор (VΣ =0,3-1,2 см3/г).
Насыпная плотность силикагеля 0,4–0,9 г/см3. Силикагель в высушенном состоянии хрупок, мало растворим и не набухает в воде и органических растворителях. Силикагель не горюч.
Слайд 792.2. Маркировка
По характеру пористой структуры силикагели подразделяются на:
крупнопористые (средний радиус
среднепористые (1,8-4,0 нм);
мелкопористые (0,8-2,0 нм).
Промышленные марки силикагелей, выпускаемых отечественными производителями, обозначают тремя буквами. Вторая буква слева всегда С, что означает силикагель. Первая буква в названии говорит о размере частиц (зерен) силикагеля: К – крупного зернения, М – мелкого зернения, Ш – шихта (смесь крупного и мелкого зернения). Буква А в названии означает активированный. Третья буква характеризует пористую структуру адсорбента: М – мелкопористый, С – среднепористый, К – крупнопористый.
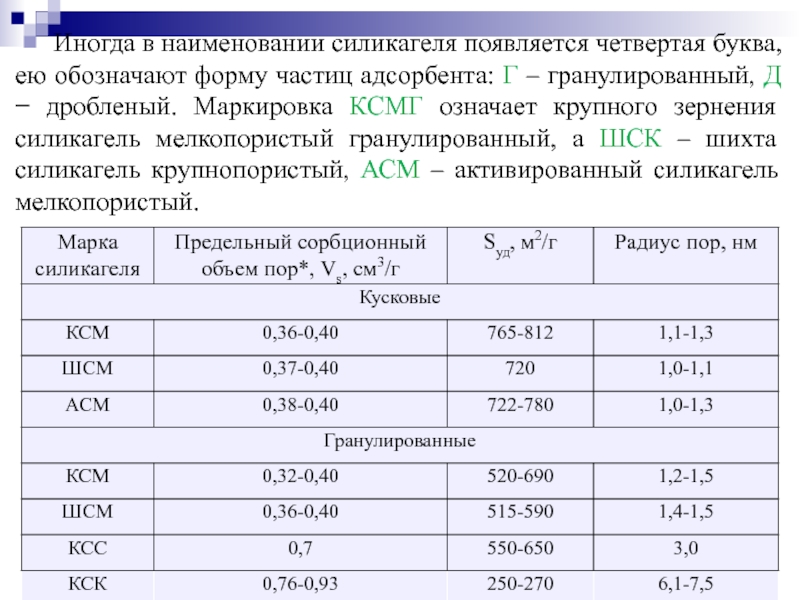
Слайд 80Иногда в наименовании силикагеля появляется четвертая буква, ею обозначают форму частиц
Слайд 812.3. Адсорбционные свойства
Силикагель обладает высокой адсорбционной способностью, избирательностью адсорбционного действия, способностью подвергаться
Адсорбция неполярных молекул на поверхности силикагеля осуществляется в основном за счет дисперсионных сил. Но адсорбционные и другие свойства силикагелей зависят от концентрации на его поверхности гидроксильных групп. Благодаря положительному заряду поверхности силикагель способен к специфическим взаимодействиям. При взаимодействии с полярными молекулами и веществами, молекулы которых имеют периферийные электроны, в энергию адсорбции помимо дисперсионного вклада вносят также вклад энергия электростатического притяжения и энергия взаимной поляризации молекул.
Слайд 82
2.4. Регенерация
При практическом применении силикагелей большое значение имеет температурный режим регенерации. Химическое
Слайд 83Критерий Пирсона
Пусть по выборке объема n получены эмпирические частоты, т.е. мы
Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты ().
При уровне значимости α требуется проверить гипотезу: генеральная совокупность распределена нормально.
В качестве критической проверку нулевой гипотезы примем случайную величину:
(*)
Эта величина случайная, т.к. в различных опытах она принимает различные, заранее не известные, значения. Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия => он характеризует близость эмпирических и теоретических распределений.
Доказано, что при закон распределения случайной величины (*) не зависит от того, какому закону распределения подчинена генеральная совокупность, а стремится к закону распределения χ2 с числом степеней свободы: υ=k–1–r , где
k – число групп (интервалов) выборки
r – число параметров предполагаемого распределения.
А т.к. для нормального распределения нам интересно М(х) и D(x), то число степеней свободы определяется υ=k–3
Правила проверки.
Слайд 84Правила проверки
Для того, чтобы при заданном уровне значимости α проверить Н0:
вычислить теоретические частоты;
вычислить наблюдаемое значение критерия:
по таблицам критических точек распределения χ2 по заданному уровню значимости и числу степеней свободы υ=k–3, найти критическую точку: χ2кр=(α,υ);
сравнить 2 имеющихся критерия:
- если χ2набл< χ2кр - нет основания отвергать нулевую гипотезу о нормальном распределении.
- если χ2набл > χ2кр - нулевую гипотезу о нормальном распределении отвергают.
Замечание:
объем выборки должен быть достаточно велик (более 50);
малочисленные группы следует объединять в одну, суммируя частоты;
т.к. возможные ошибки первого и второго рода, то в окончательном выводе следует проявить осторожность:
можно повторить опыт;
увеличить число наблюдений;
для проверки воспользоваться другими критериями;
построить график распределения;
вычислить эксцесс и асимметрию.
для контроля вычислений формулу преобразуют к виду
Слайд 85Корреляционно-регрессионный анализ
Корреляционная зависимость
Корреляционный момент
Коррелированность и зависимость случайных величин
Выборочное корреляционное отношение
Простейшие случаи
Метод наименьших квадратов
Слайд 86Во многих задачах требуется установить или оценить зависимость изучаемо случайной величины
Две случайные величины могут быть связаны:
- функциональной зависимостью
- статистической
- независимой
Строгая функциональная зависимость реализуется редко, т.к. обе случайных величины или одна подвержены действию других случайных величин.
Статистической называется зависимость, при которой
изменение одной из величин влечет изменение распределения
другой.
В частности она проявляется в том что изменение одной из величин влечет изменение среднего значения другой. Такая статистическая зависимость называется корреляционной.
Слайд 87Корреляционная зависимость
Предположим изучается связь между случайными величинами Х и Y. Пусть
Условным средним называется среднее арифметическое случайной величины Y соответствующее значению случайной величины Х равное х.
Если каждому значению Х соответствует одно значение , то очевидно что она – функция от х. В этом случае говорят, что случайная величина Y зависит от Х корреляционно.
Корреляционной зависимостью Yx называют функциональную зависимость от значений х. = f(x) - уравнение регрессии Y на Х, а график – линией регрессии Y на Х. f(x) – функция регрессии.
Аналогично определяется условная средняя Х на Y: = f(y).
Две основные задачи теории корреляции:
Оценить тесноту (силу) корреляционной связи
Если связь существует, то нужно установит ее форму – вид функциональной зависимости между и величиной Х.
Для решения первой задачи существует коэффициент корреляции.
Слайд 88Коэффициент корреляции.
Выборочным коэффициентом корреляции называется отношение разности между М(Х) произведения случайных
Он служит для оценки тесноты линейной корреляционной зависимости.
Свойства коэффициента корреляции
rв по абсолютной величине ≤ 1
Если rв= 0, то Х и Y не связаны линейной зависимостью, а другая может при этом существовать.
Если |rв| = 1, то Х и Y связаны строго корреляционной зависимостью.
Т.к. rв характеризует степень тесноты линейной связи, то она проявляется в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать, т.е. наблюдается положительная корреляция, rв>0; если при возрастании одной случайной величины другая – убывает, rв<0.
Remark: Зависимость тем ближе к линейному закону, чем |rв| ближе к единице.
Для описания системы двух случайных величин или зависимости между двумя случайными величинами, кроме математического ожидания и дисперсии используют и другие величины. Коэффициент корреляции rв является частным случаем такой характеристики, более частным случаем выступает корреляционный момент μху.
Слайд 89Корреляционный момент
Корреляционным моментом μху случайных величин Х и Y,
называют
величин.
μху = М [(Х – М(Х))*(Y – М(Y))]
μху = М (Х*Y) – М(Х)*М(Y)
rв = μху / σх*σу
Свойства корреляционного момента:
корреляционный момент служит для характеристики связи между случайными величинами Х и Y;
корреляционный момент двух независимых величин равен нулю;
корреляционный момент имеет размерность равную произведению размерности величин Х и Y;
размерность корреляционного момента является недостатком при сравнении зависимости двух случайных величин, чтобы избежать это, был введен коэффициент корреляции.
Слайд 90Коррелированность и зависимость случайных величин
Две случайных величин называются коррелированными, если их
Х и Y называются некоррелированными случайными величина-ми, если их корреляционный момент равен нулю;
Две коррелированные величины также зависимы. Обратное предположение не всегда имеет место.
Слайд 91Выборочное корреляционное отношение
Для оценки тесноты нелинейной корреляционной связи служат такие характеристики
Выборочным корреляционным отношением называется, отношение межгруппового
среднеквадратического отклонения к общему среднеквадратическому отклонению.
ηух = σмехгр / σобщ
Свойства корреляционного отношения:
если корреляционное отношение равно нулю, Х и Y не связаны друг с другом;
если корреляционное отношение = 1, Х и Y не связаны корреляционной зависимостью;
значение корреляционного отношения удовлетворяет двойному неравенству 0 ≤ ηух ≤ 1;
корреляционное отношение всегда меньше или равно коэффициенту корреляции ηух ≤ |rв|.
Слайд 92Достоинства корреляционного отношения.
Корреляционное отношение служит мерой тесноты связи любой, в том
Недостатки корреляционного отношения.
Корреляционное отношение не позволяет судить на сколько близко расположены точки найденным по данным наблюдения к кривой определенного вида (гипербола, парабола, синусоида и т.д.). Это объясняется тем, что при определении корреляционного отношения вид связи не учитывается.
Слайд 93Простейшие случаи криволинейной корреляции
Если график регрессии Y на Х изображен кривой
Примеры функции регрессии
Параболическая корреляция второго порядка = ах² + вх + с
Параболическая корреляция третьего порядка =а+вх²+сх + d
Гиперболическая = а/х + в
Для определения вида функции регрессии строят на графике точки с координатами (х, ). По их расположению делают заключение о примерном виде функции регрессии.
При окончательном решении принимают во внимание особенности, вытекаемые из сущности решаемой задачи.
Теория криволинейной корреляции решает те же задачи что и теория линейной корреляции, т.е. устанавливает формы и тесноты корреляционной зависимости.
Неизвестные параметры уравнения регрессии ищут методом «наименьших квадратов».
Слайд 94Метод наименьших квадратов
Метод наименьших квадратов заключается в том, что сумма квадратов
Будем искать уравнение регрессии в виде у = f(x).
Предположим, что имеет место линейная зависимость φ(х)= а0 +а1х
а0, а1 – коэффициенты линейной зависимости
φ(х) – предполагаемая теоретическая зависимость
Используя метод наименьших квадратов построим функцию равную сумме квадратов отклонений экспериментальных данных от теоретических данных:
По методу наименьших квадратов для нахождения коэффициентов а0, а1, необходимо составить систему двух уравнений, для этого необходимо взять частные производные от функции S и приравнять их к нулю.
Учитывая число функций φ(х)=а0+а1х
Окончательной системой уравнений по методу наименьшего квадрата имеет вид
Решая полученную систему найдем неизвестные коэффициенты а0 и а1, запишем уравнение регрессии в виде φ(х) = а0 + а1х
Слайд 95Для того чтобы найти погрешность данного метода необходимо вычислить
Если предположили
φ(х)=а0+а1х+а2х², то аналогично по методу наименьших квадратов найдем функцию
Находим частные производные данной функции
Запишем систему уравнений
Аналогично находим а0, а1, а2 и записываем уравнение регрессии в виде φ(х)=а0+а1х+а2х²
Определяем погрешность с помощью ε.
Заключение о реальной зависимости между случайными величинами Х и Y делаем путем графического представления.
Слайд 96Если нужно отобрать 20% изготовленных деталей, то отбирают каждую пятую.
Детали изготавливаются
Изделия изготавливаются станками-автоматами. Обследованию подвергается продукция нескольких автоматов.
Слайд 97Задано распределение частот выборки.
Определить объем, написать распределение относительных частот.
n=3+10+12=20
Σ Wi=1
Σ ni=n
Слайд 98Пусть имеется нормальное распределение. Тогда нужно оценить, найти M(x) и σ.
Слайд 99Найти доверительный интервал с надежностью 0.9 неизвестного M(X) нормально распределенной СВ
2Φ(t)=σ
Φ(t)=β/2=0.45
t=1.645
=0.82
(20.9–0.82; 20.9+0.82)
(20.08; 21.72)
Слайд 100По данным выборки, объема 50, найдена =-0.155, S=936. Найти доверительный
По таблицам распределения Стьюдента для уровня значимости α=0.05 и числа степеней свободы υ=49 найдем значение критерия Стьюдента tα,υ=2.009
Запишем значение границы интервала =0.27
Запишем границы доверительного интервала (-0.425;0.115).
С вероятностью 0.95 истинное значение М(х) лежит в пределах (-0.425;0.115).
Слайд 101При доверительной вероятности 90% найти доверительный интервал для D(x), если для
По таблицам распределения χ2 найдем значение критерия χ2 для уровня значимости υ=4 и α=/2=0.05
χ20.05,4=9.5
χ2 α/2,υ = χ20.95,4=0.711
4.6.6/9.5 < σ2 < 4.6.6/0.711
2.78 < σ2 < 37.13
Слайд 102Если Н0 состоит в предположении, что математическое ожидание М(Х) нормального распределения
Н0: М(Х)=10
Н1: М(Х)≠10
Слайд 103По двум малым независимым выборкам объемов nx=11 и ny=14 из нормальных
Решение: Найдем отношение большей исправленной дисперсии к меньшей:
Fнабл = S²б / S²м = 0.76 / 0.38 = 2
По условию конкурирующая гипотеза имеет вид Н1: Dx>Dy, поэтому критическая область – правосторонняя. По таблице критических то-чек распределения Фишера, по уровню значимости α=0,05 и числам степеней свободы k1 = nx – 1 = 11 – 1 = 10 и
k2 = ny – 1 = 14 – 1 = 13 находим критическую точку:
Fкр (α, kı, k2) = Fкр (0.05,10,13) = 2.67
Так как Fнабл = 2. < Fкр = 2.67, то нет оснований отвергать Но о равенстве дисперсий. Другими словами, исправленные выборочные дисперсии различаются незначимо.