- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересечение прямых и плоскостей презентация
Содержание
- 1. Пересечение прямых и плоскостей
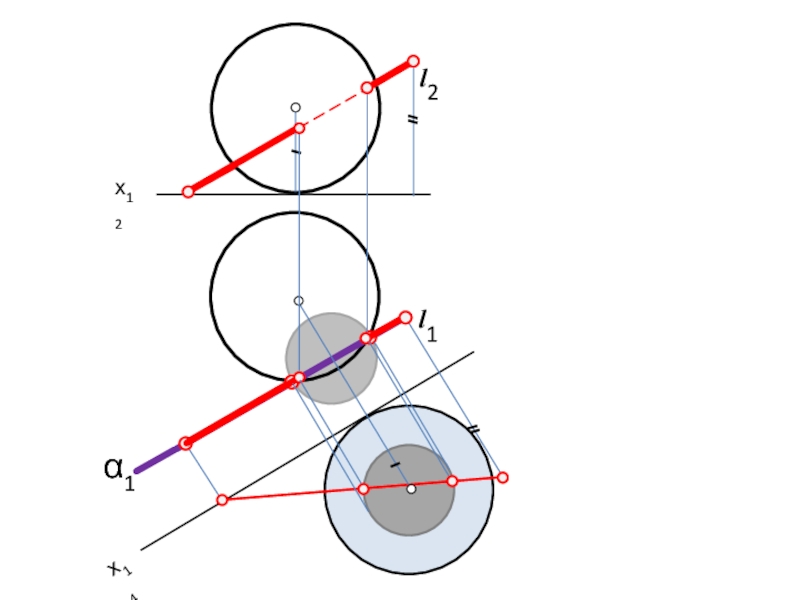
- 2. k2 ω2 k1 x12
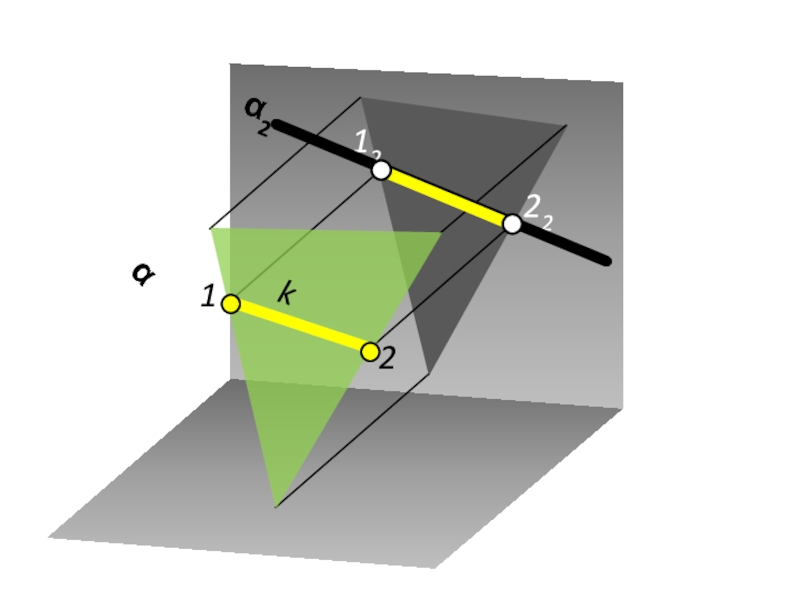
- 3. Пересечение плоскости общего положения с проецирующей плоскостью
- 4. α2 k
- 5. α2 12 22
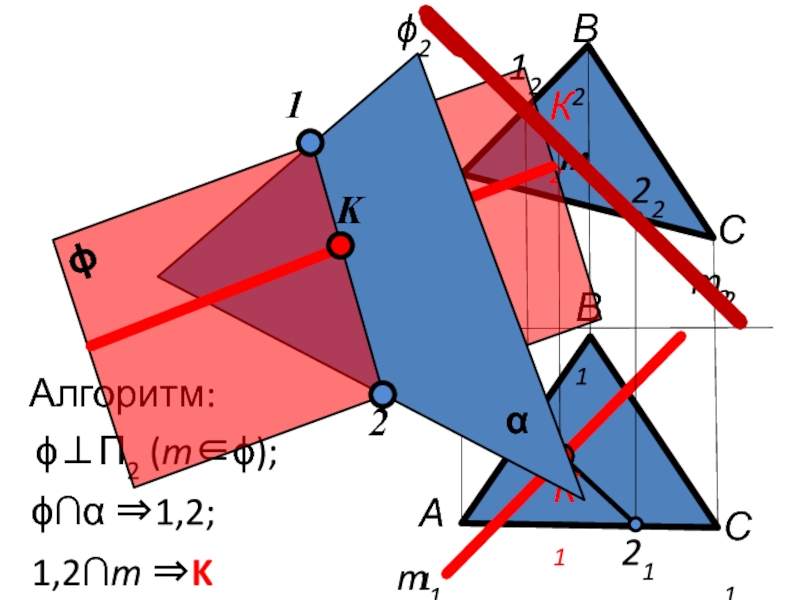
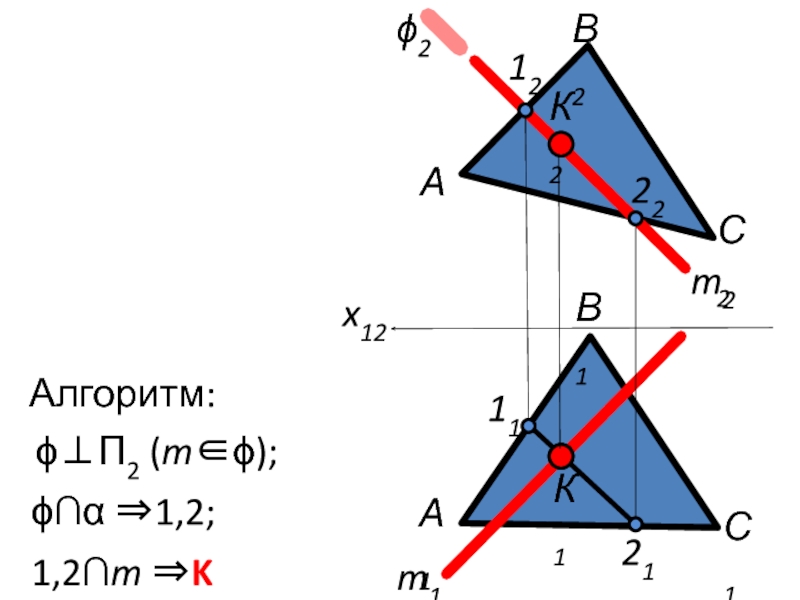
- 6. Пересечение прямой с плоскостью общего положения
- 7. α ϕ m
- 8. x12 m2 m1 ϕ2
- 9. x12 m2 m1 ϕ2
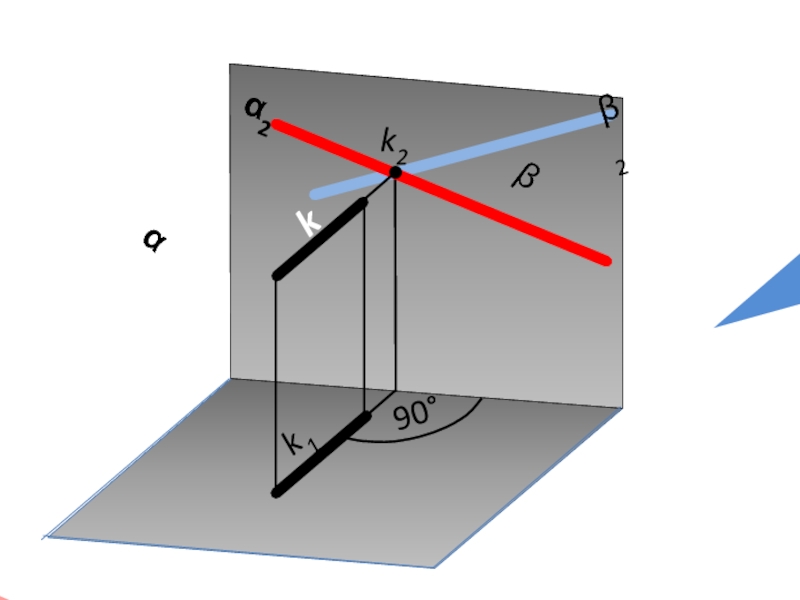
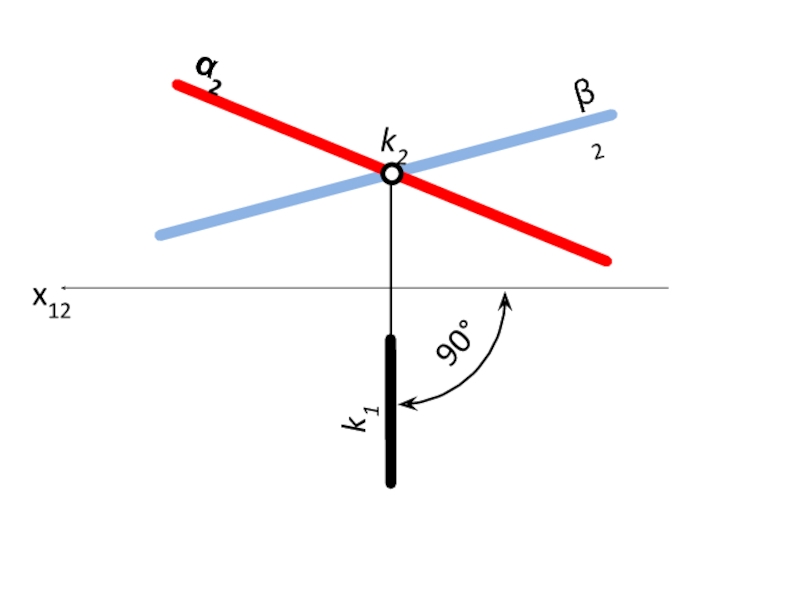
- 10. Пересечение проецирующих плоскостей
- 11. α β2 α2 k k2 k1 β 90°
- 12. β2 α2 k2 k1 x12 90°
- 13. Построение линии пересечения двух плоскостей общего положения
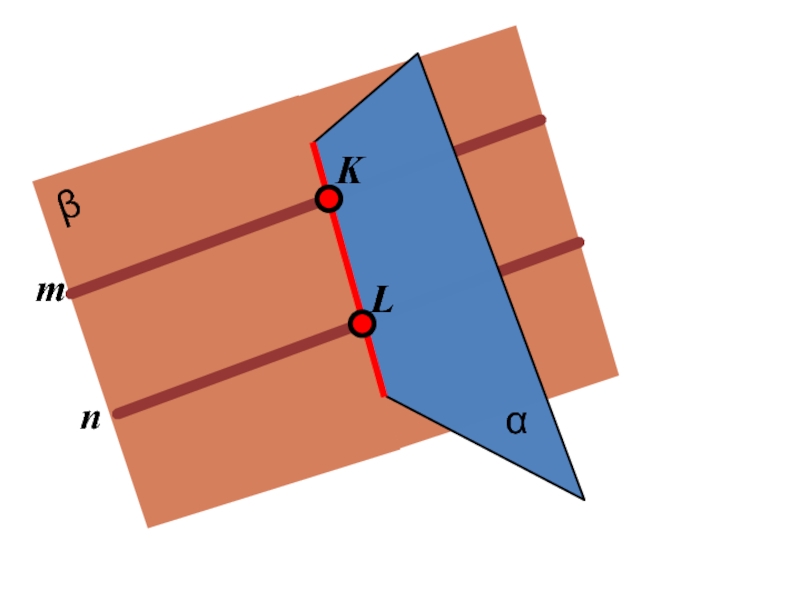
- 14. α m K L β n
- 15. α m K L β n К L
- 16. α m β n
- 18. a2 b2 e2
- 19. α(a∩b) и β(eff) ω⊥П2 ϕ⊥
- 20. Пересечение плоскости с проецирующей плоскостью
- 21. Линией пересечения двух плоскостей является прямая, принадлежащая
- 22. Определение видимости плоскостей
- 23. А2 В2 С2 С1
- 24. Пересечение поверхности плоскостью и прямой
- 25. Пересечение проецирующей плоскости с поверхностью многогранника
- 27. А2 В2
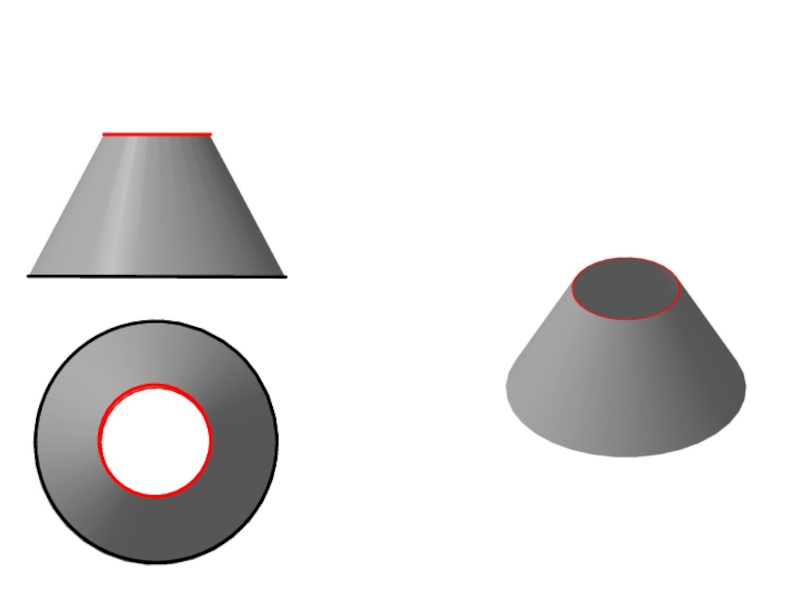
- 28. Пересечение с линейчатой поверхностью
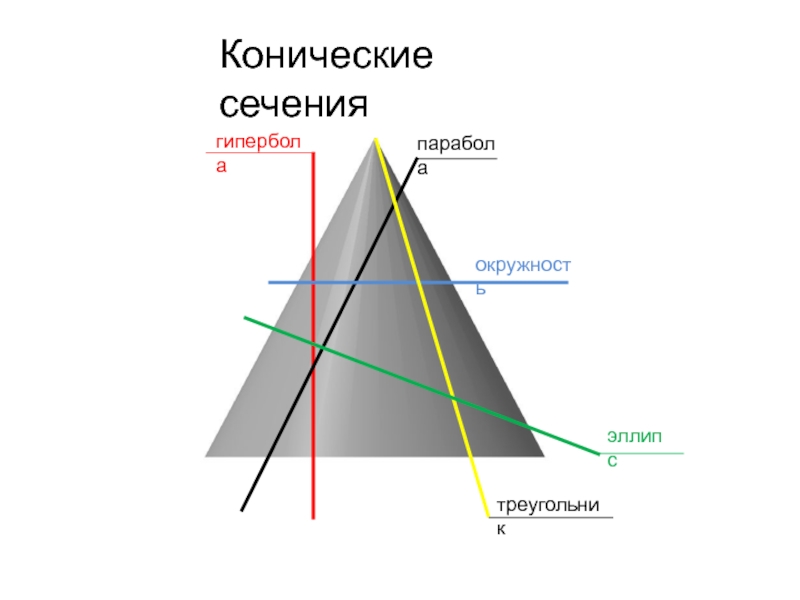
- 29. парабола
- 30. гипербола
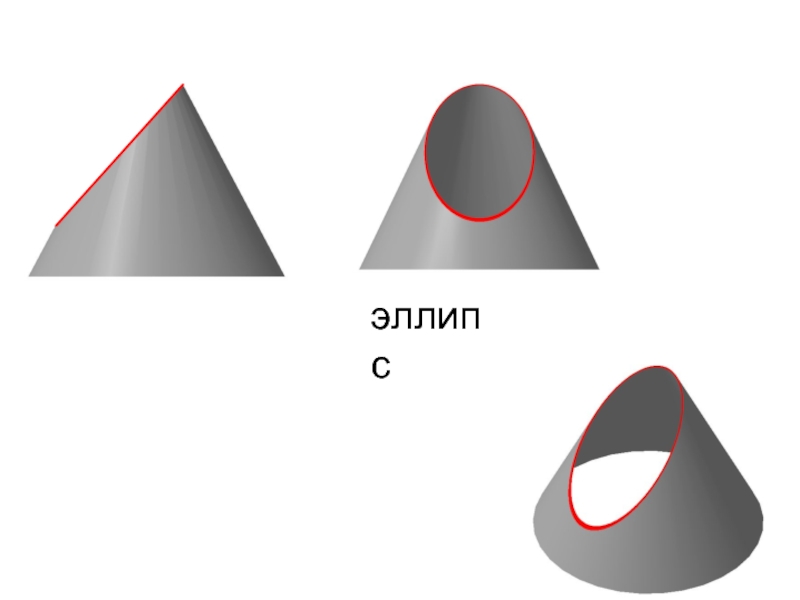
- 31. эллипс
- 34. Конические сечения гипербола парабола окружность треугольник эллипс
- 35. ϕ2
- 36. Алгоритм На поверхности обозначить
- 37. ϕ2 (12)
- 38. Алгоритм На поверхности обозначить
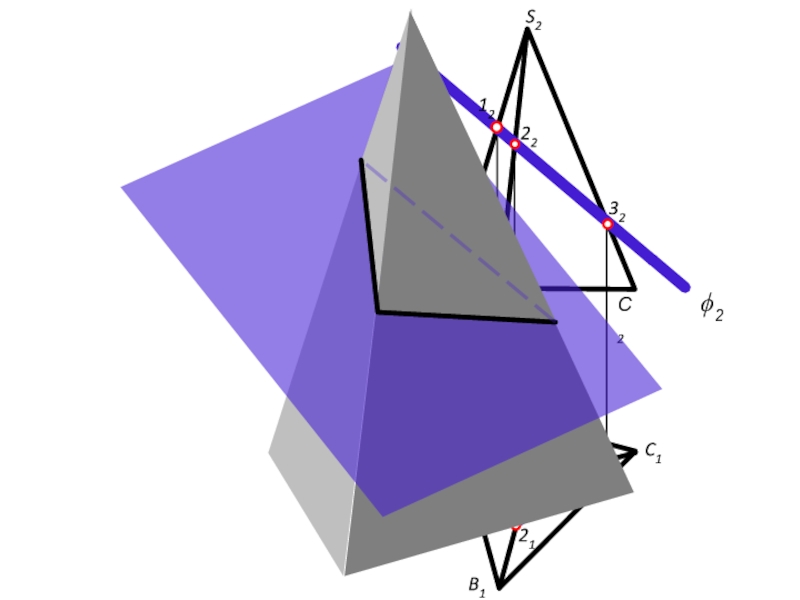
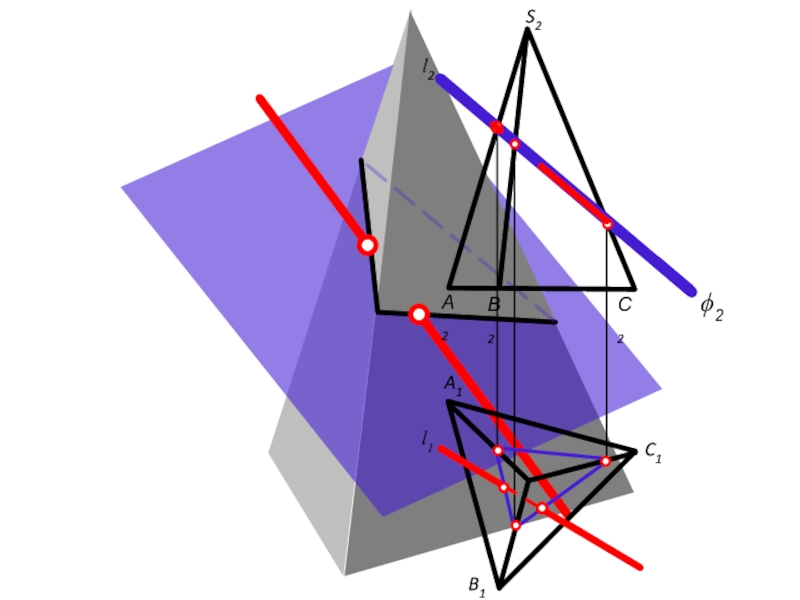
- 39. Пересечение прямой с гранными поверхностями
- 41. А2 В2
- 42. Алгоритм построения точек пересечения прямой с поверхностью
- 43. Пересечение прямой с линейчатой поверхностью
- 45. Алгоритм построения точек пересечения прямой с поверхностью
- 49. α2 l2 N2 M2
- 50. l2 M2 N2 ≡ M1 N1 ϕ2 l1
- 53. 1 2 1 2 3 4 3
- 54. Алгоритм построения точек пересечения прямой ОП
- 57. α1 х14 х12
- 58. Алгоритм построения точек пересечения прямой ОП
- 59. Х m2 m1 ϕ2
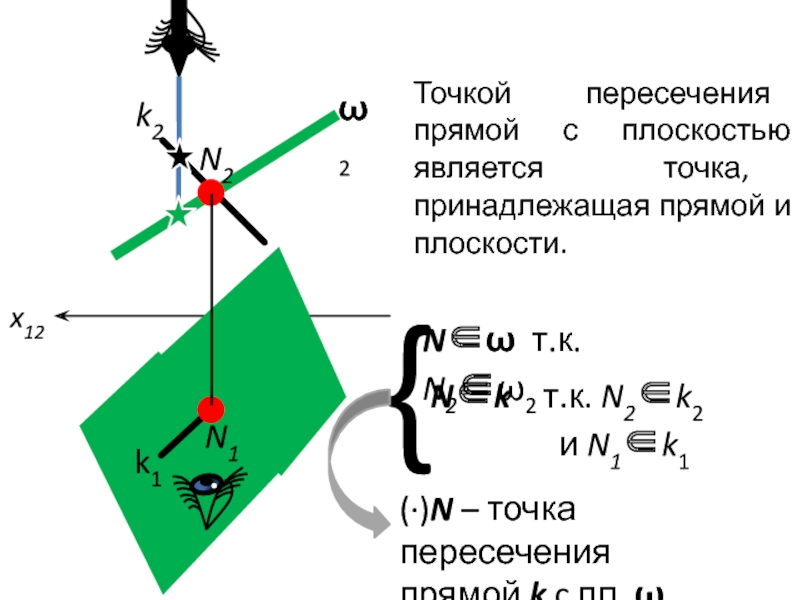
Слайд 2
k2
ω2
k1
x12
N2
N1
Точкой пересечения прямой с плоскостью является точка, принадлежащая прямой и плоскости.
N∈ω
т.к. N2∈ω2
N∈k т.к. N2∈k2
и N1∈k1
}
(∙)N – точка пересечения
прямой k c пл. ω
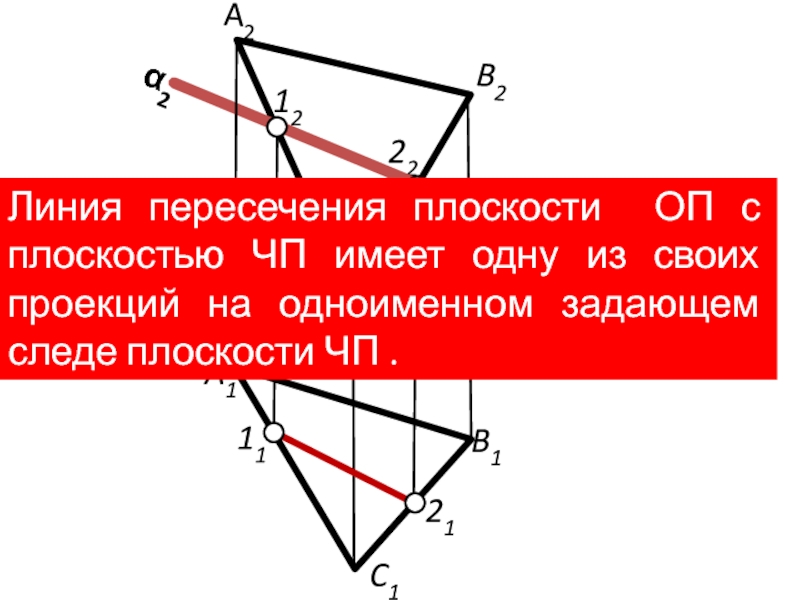
Слайд 5
α2
12
22
A2
B2
C2
A1
B1
C1
x12
11
21
Линия пересечения плоскости ОП с плоскостью ЧП имеет одну из своих
проекций на одноименном задающем следе плоскости ЧП .
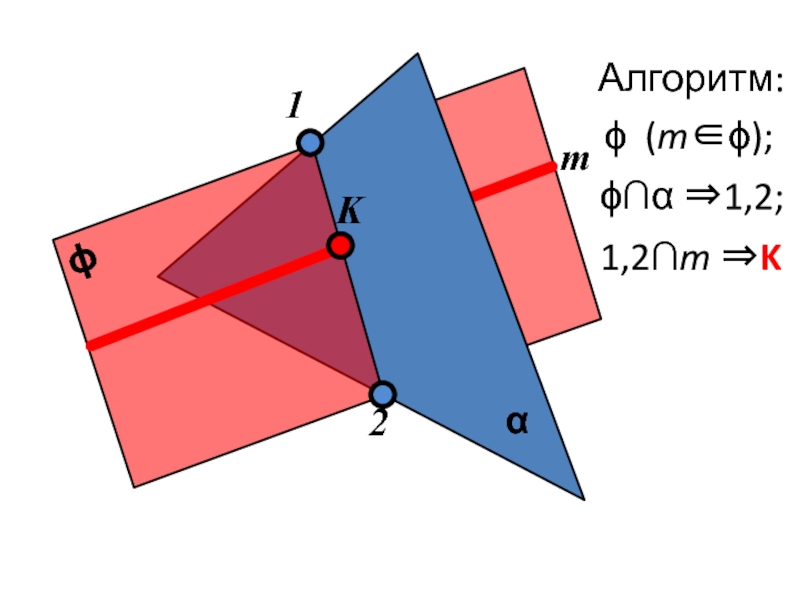
Слайд 16
α
m
β
n
L
K
Построение линии пересечения двух плоскостей общего положения заключается в определении точек
пересечения двух прямых одной плоскости с другой плоскостью
Слайд 18
a2
b2
e2
f2
ϕ2
ω2
b1
a1
12
22
32
42
41
31
21
11
52
62
61
51
M1
N1
N2
M2
e1
f1
α(a∩b)
β(eff)
ω⊥П2
ϕ⊥ П2
ω∩α⇒12
12∩34⇒M
ω∩β⇒34
ϕ∩α⇒5…
ϕ∩β⇒6…
5…∩6…⇒N
Слайд 19α(a∩b)
и β(eff)
ω⊥П2
ϕ⊥ П2
ω∩α⇒12
}
ω∩β⇒34
ϕ∩α⇒5…
ϕ∩β⇒6…
}
5…∩6…⇒N
12∩34⇒M
}
MN – линия
пересечения
плоскостей
α и β
Алгоритм
построения линии пересечения
двух плоскостей общего положения
двух плоскостей общего положения
Слайд 21Линией пересечения двух плоскостей является прямая, принадлежащая обеим плоскостям.
А2
В2
С2
А1
В1
С1
ϕ2
12
22
12
22
x12
12 ∈ϕ т.к.
1222≡ϕ2
12 ∈ΔАВС т.к.
(∙)1∈АС;
(∙)2∈ВС
{
12 - линия пересечения пл.ϕ и пл. ΔАВС
Плоскость ϕ ⊥П2
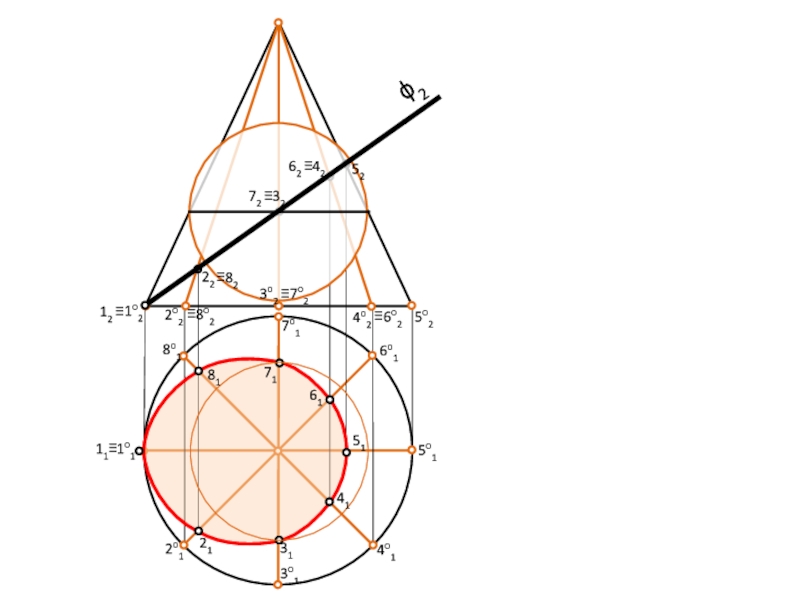
Слайд 35
ϕ2
1о1
2о1
3о1
4о1
5о1
6о1
7о1
8о1
≡8о2
2о2
3о2
4о2
5о2
≡6о2
≡7о2
1о2
21
51
71
31
41
61
81
11≡
12 ≡
22
32
42
62 ≡
52
72 ≡
≡82
Слайд 36Алгоритм
На поверхности обозначить ряд образующих. Обязательно включить
очерковые образующие с П1 и П2.
Обозначить точки пересечения проецирующей плоскости с образующими.
Перенести точки на другую плоскость проекций. Соединить полученные проекции точек плавной кривой.
Показать видимость линии пересечения.
Обозначить точки пересечения проецирующей плоскости с образующими.
Перенести точки на другую плоскость проекций. Соединить полученные проекции точек плавной кривой.
Показать видимость линии пересечения.
Слайд 38Алгоритм
На поверхности обозначить ряд точек на следе
плоскости. Обязательно включить точки, лежащие на экваторе и главном меридиане.
Перенести точки, лежащие на экваторе и главном меридиане на другую плоскость проекций.
На поверхности обозначить ряд параллелей на П1 и П2.
Обозначить точки пересечения проецирующей плоскости с параллелями.
Перенести точки на другую плоскость проекций.
Соединить полученные проекции точек плавной кривой.
Показать видимость линии пересечения.
Перенести точки, лежащие на экваторе и главном меридиане на другую плоскость проекций.
На поверхности обозначить ряд параллелей на П1 и П2.
Обозначить точки пересечения проецирующей плоскости с параллелями.
Перенести точки на другую плоскость проекций.
Соединить полученные проекции точек плавной кривой.
Показать видимость линии пересечения.
Слайд 42Алгоритм построения точек пересечения прямой с поверхностью
l ∈ пл. ϕ;
пл. ϕ ∩ с поверхностью τ ⇒ линия d;
линия d ∩ l ⇒ (∙∙∙) M, N.
линия d ∩ l ⇒ (∙∙∙) M, N.
Слайд 45Алгоритм построения точек пересечения прямой с поверхностью
l ∈ пл. ϕ;
пл. ϕ ∩ с поверхностью τ ⇒ линия d;
линия d ∩ l ⇒ (∙∙∙) M, N.
линия d ∩ l ⇒ (∙∙∙) M, N.
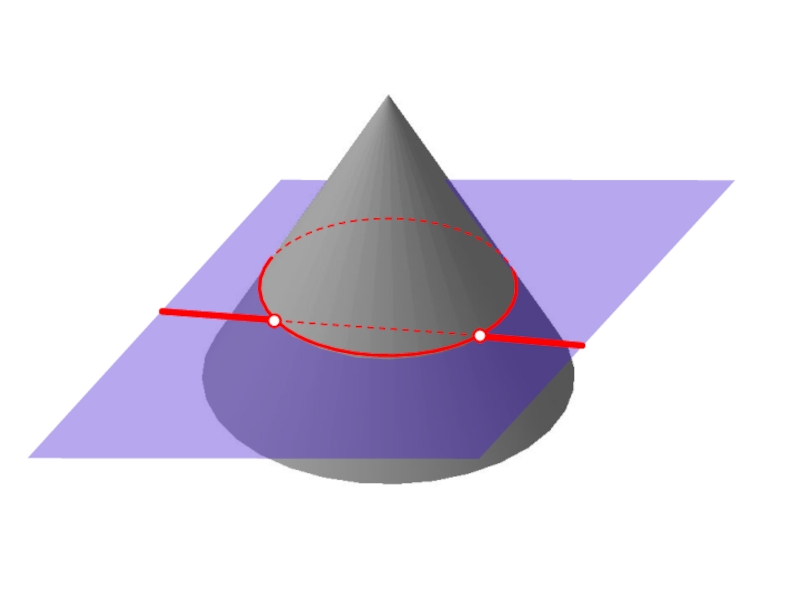
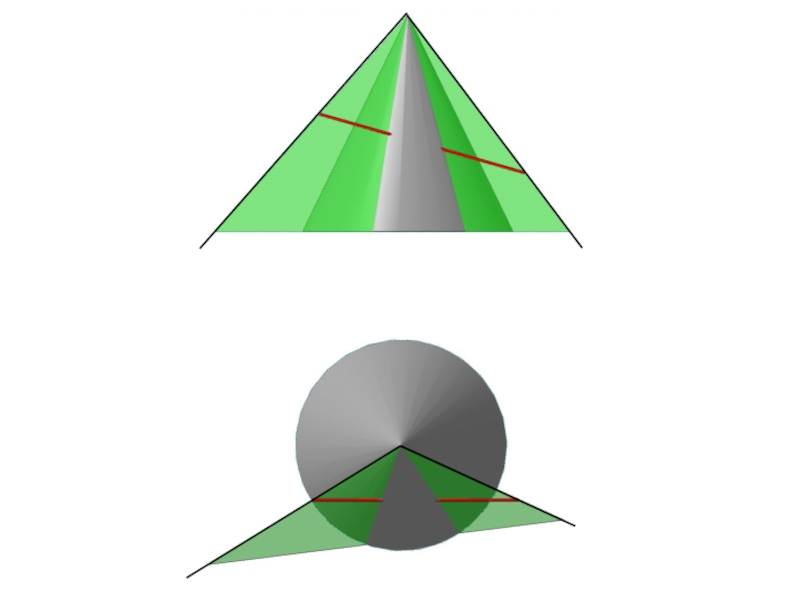
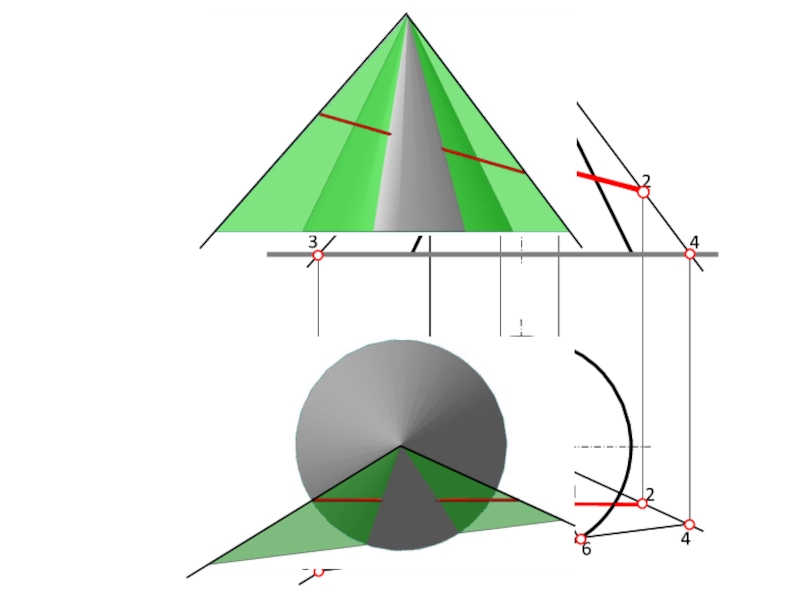
Слайд 54Алгоритм построения точек пересечения
прямой ОП с конусом
Выбрать (∙)
1 и (∙) 2 на прямой.
Через вершину конуса и (∙) 1 и (∙) 2 провести лучи.
На пересечении лучей с плоскостью основания конуса построить (∙) 3 и (∙) 4.
Построить линию 34 .
На пересечении линии с очерком основания конуса построить (∙) 5 и (∙) 6 .
Построить образующие конуса из (∙) 5 и (∙) 6 .
На пересечении образующих с прямой построить (∙) М и (∙) N.
Через вершину конуса и (∙) 1 и (∙) 2 провести лучи.
На пересечении лучей с плоскостью основания конуса построить (∙) 3 и (∙) 4.
Построить линию 34 .
На пересечении линии с очерком основания конуса построить (∙) 5 и (∙) 6 .
Построить образующие конуса из (∙) 5 и (∙) 6 .
На пересечении образующих с прямой построить (∙) М и (∙) N.
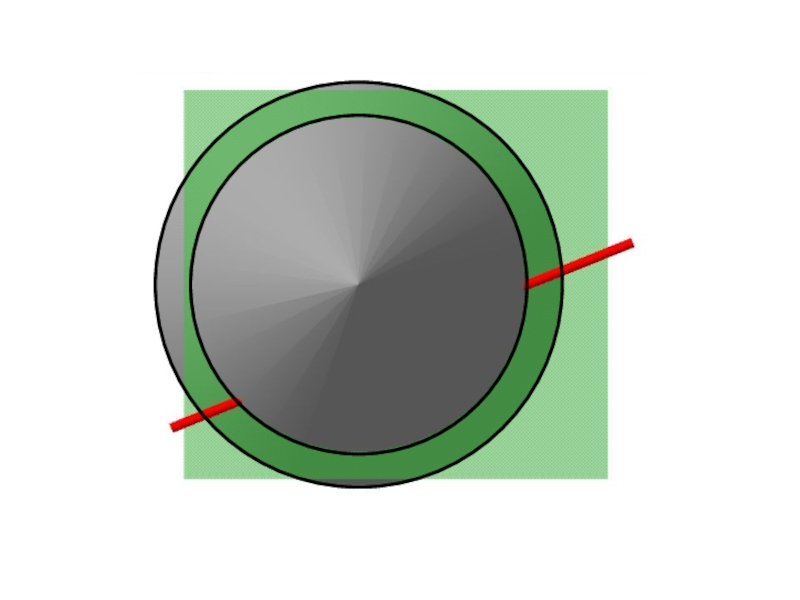
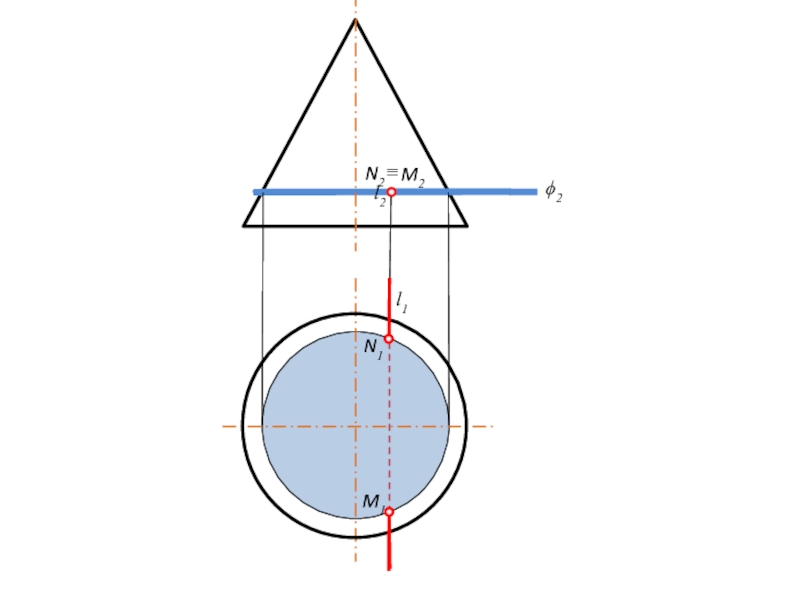
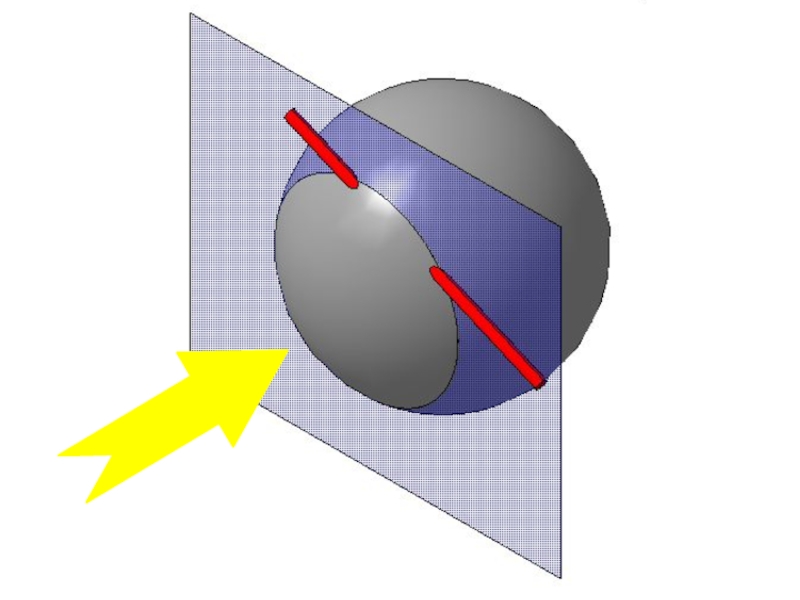
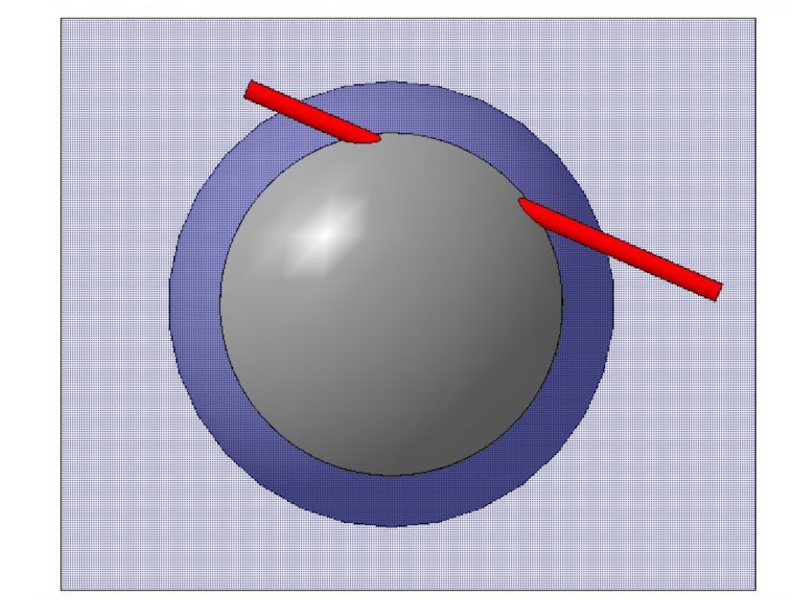
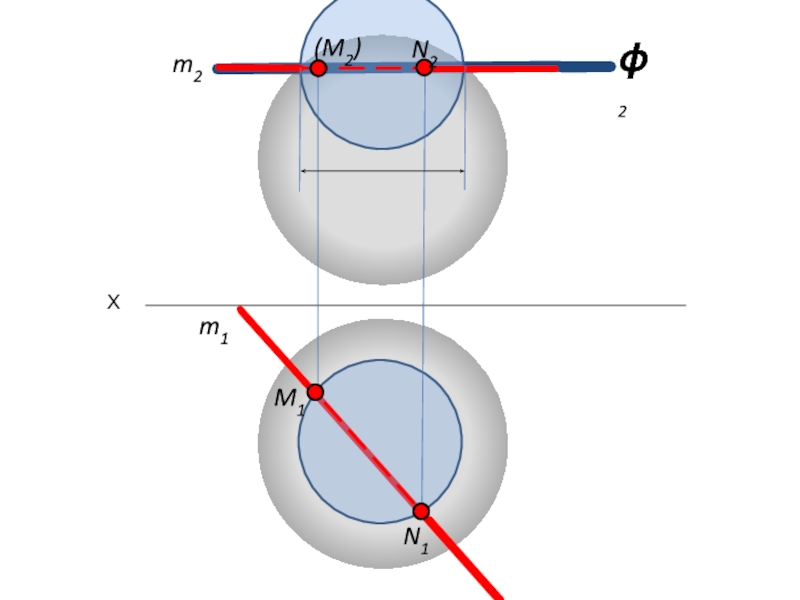
Слайд 58Алгоритм построения точек пересечения
прямой ОП со сферой
Заключить прямую l
в проецирующую плоскость α.
Ввести дополнительную плоскость проекций Пi+1 || α.
На пл. Пi+1 построить центр сферы О и прямую l.
Из центра Оi+1 построить сечение сферы плоскостью α (окружность).
Обозначить точки пересечения проекций сечения сферы и прямой на пл. Пi+1 .
Точки перенести с плоскости Пi+1 на плоскости проекций Пi , П1, П2.
Ввести дополнительную плоскость проекций Пi+1 || α.
На пл. Пi+1 построить центр сферы О и прямую l.
Из центра Оi+1 построить сечение сферы плоскостью α (окружность).
Обозначить точки пересечения проекций сечения сферы и прямой на пл. Пi+1 .
Точки перенести с плоскости Пi+1 на плоскости проекций Пi , П1, П2.