Татьяна Валентиновна
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Плоскость. Позиционные и метрические задачи. (Лекция 2) презентация
Содержание
- 1. Плоскость. Позиционные и метрические задачи. (Лекция 2)
- 2. План лекции Способы задания плоскостей Проецирование плоскости
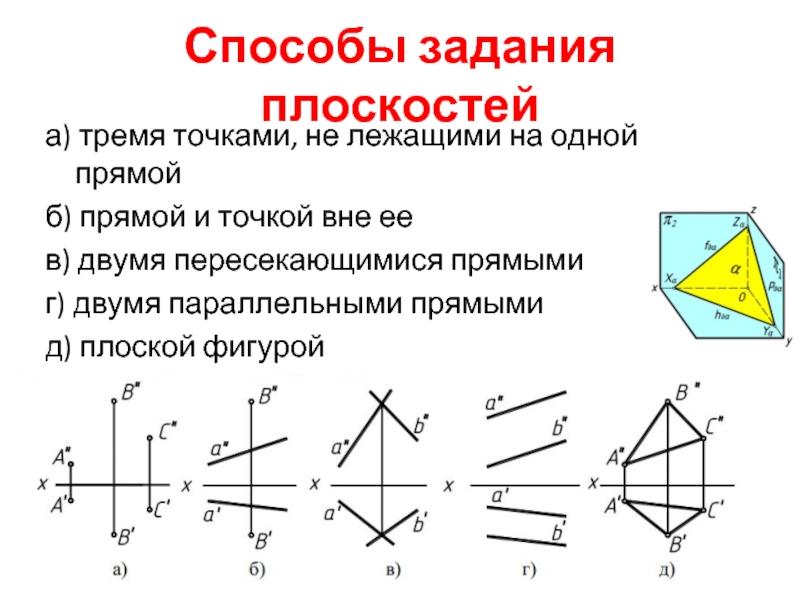
- 3. Способы задания плоскостей а) тремя точками, не
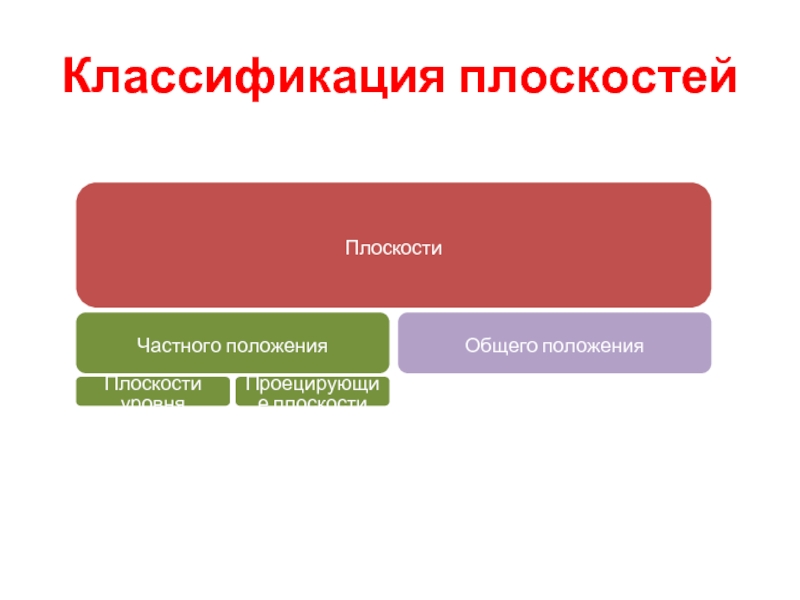
- 4. Классификация плоскостей Плоскости Частного положения Плоскости уровня Проецирующие плоскости Общего положения
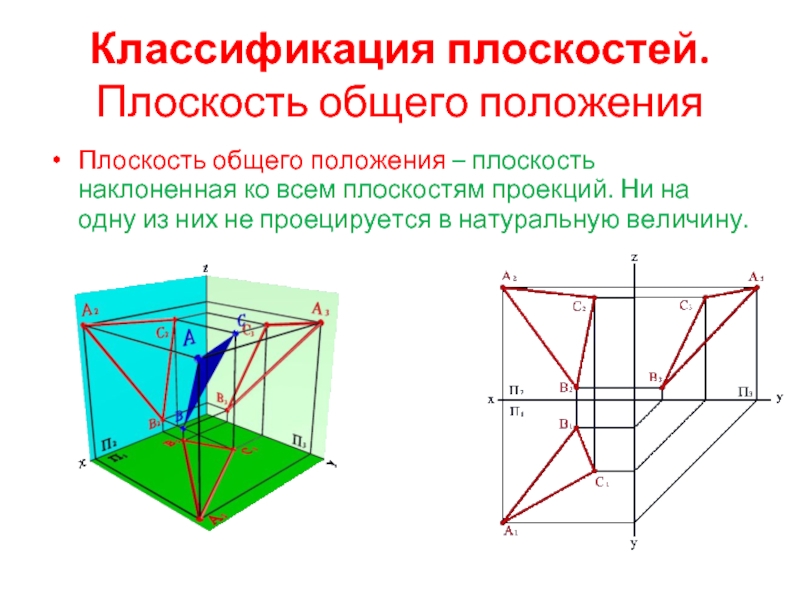
- 5. Классификация плоскостей. Плоскость общего положения Плоскость общего
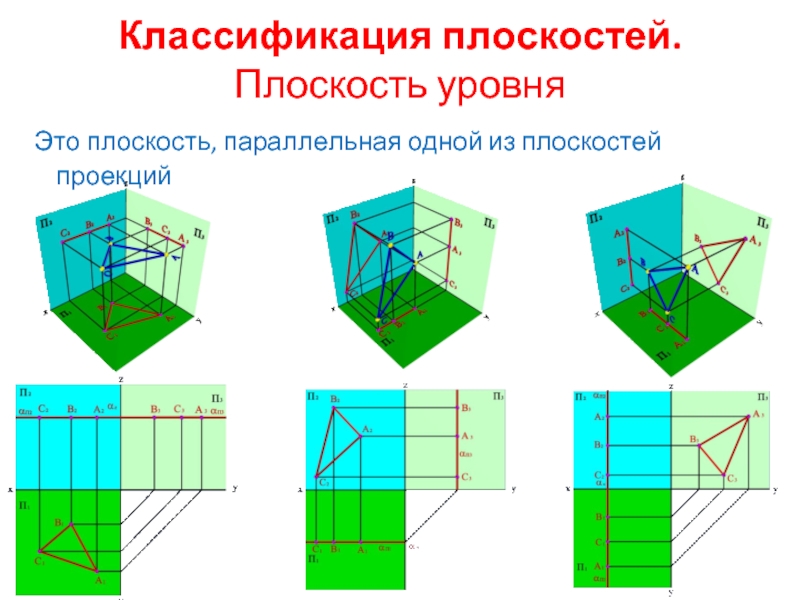
- 6. Классификация плоскостей. Плоскость уровня Это плоскость, параллельная одной из плоскостей проекций
- 7. Классификация плоскостей. Проецирующая плоскость Это плоскость, перпендикулярная одной из плоскостей проекций
- 8. Принадлежность прямой плоскости Прямая принадлежит плоскости, если
- 9. Принадлежность точки плоскости Точка
- 10. Главные линии плоскости Горизонталь (h2 ║ x, h1 ║ P1)
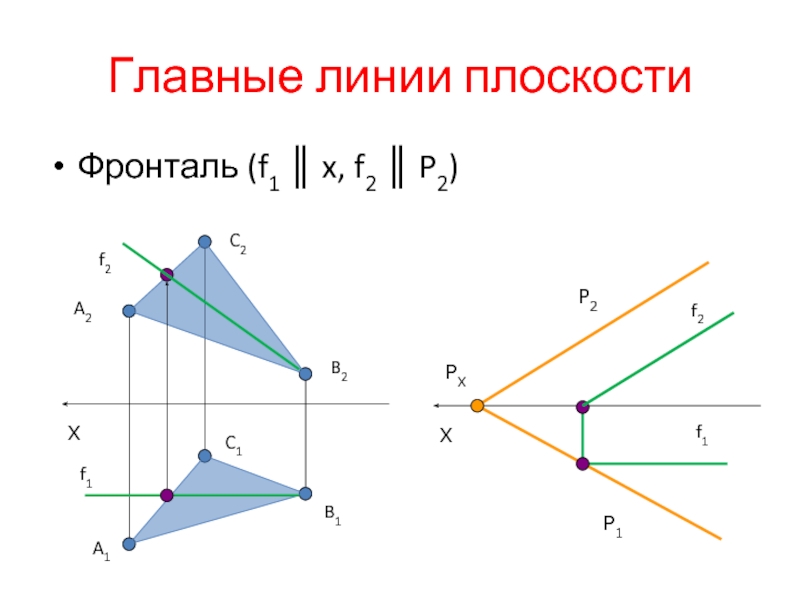
- 11. Главные линии плоскости Фронталь (f1 ║ x, f2 ║ P2)
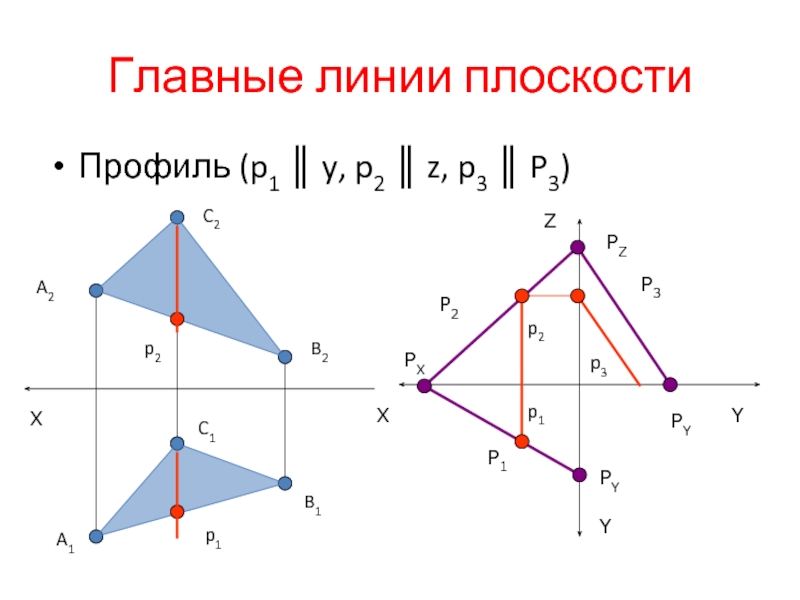
- 12. Главные линии плоскости Профиль (p1 ║ y, p2 ║ z, p3 ║ P3)
- 13. Главные линии плоскости Линия ската – линия,
- 14. Определение угла наклона плоскости ОП к плоскостям
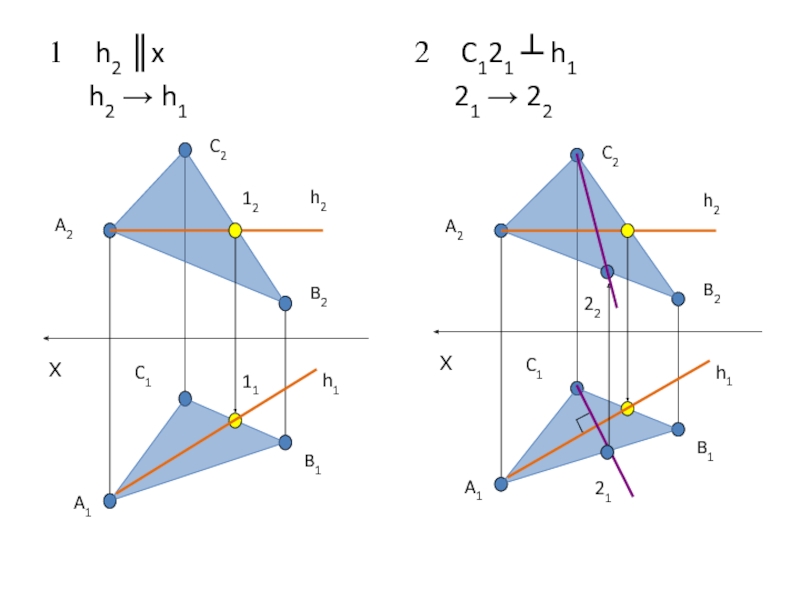
- 15. h2 ║x h2 → h1 C121 ┴ h1 21 → 22
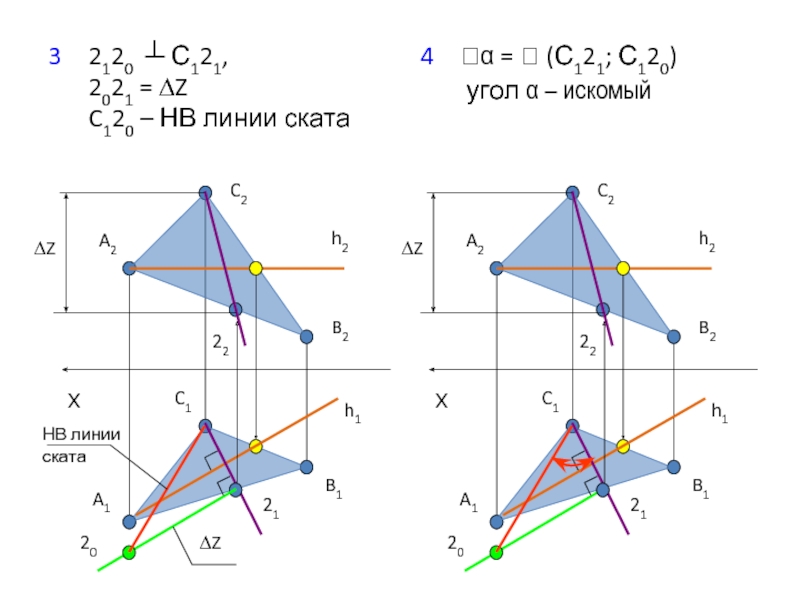
- 16. 3 2120 ┴ С121, 2021 = ∆Z C120
- 17. Взаимное положение прямой и плоскости Прямая параллельна
- 18. Взаимное положение прямой и плоскости Прямая перпендикулярна
- 19. Пересечение прямой с плоскостью частного положения Дано:
- 20. Пересечение плоскостей частного и общего положения Дано:
- 21. Пересечение прямой с плоскостью ОП Алгоритм решения:
- 22. 1 n(n1, n2) Є Σ (Σ1), ┴
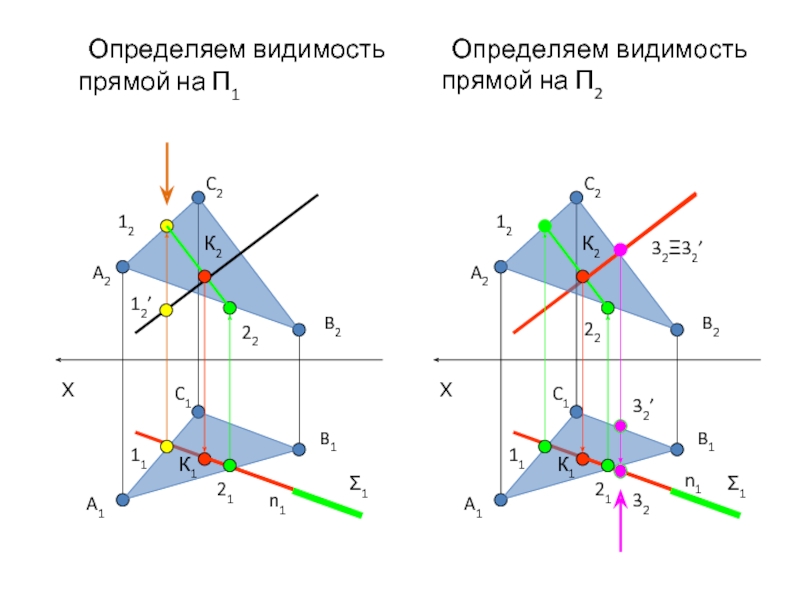
- 23. Определяем видимость прямой на П1 Определяем видимость прямой на П2
- 24. Позиционные и метрические задачи 1 Определение
- 25. 1 Σ(h ∩ f): f2 ┴m2, f1║x
- 26. 3 АК – расстояние от точки А
- 27. Позиционные и метрические задачи 2 Определение расстояния от
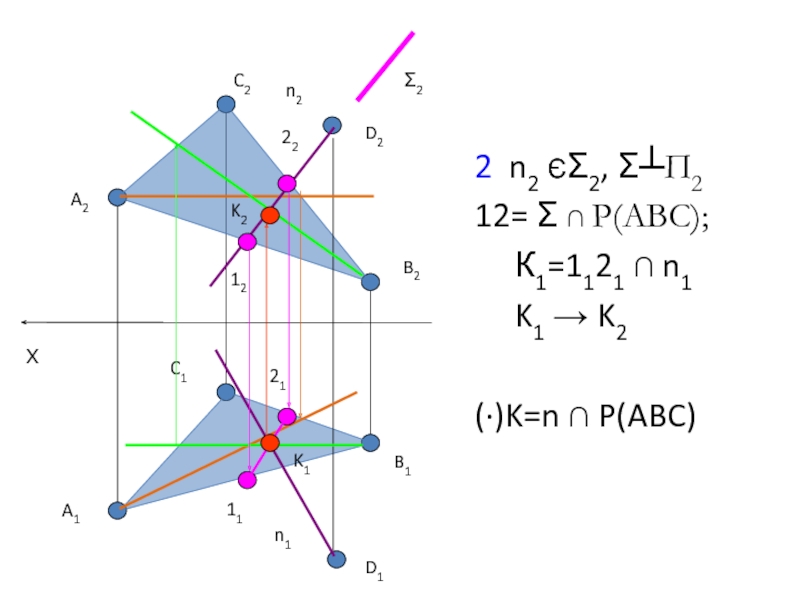
- 28. 1 n ┴ P(∆ABC) : n1┴ h1; n2 ┴ f2
- 29. 2 n2 ЄΣ2, Σ┴П2 12= Σ ∩
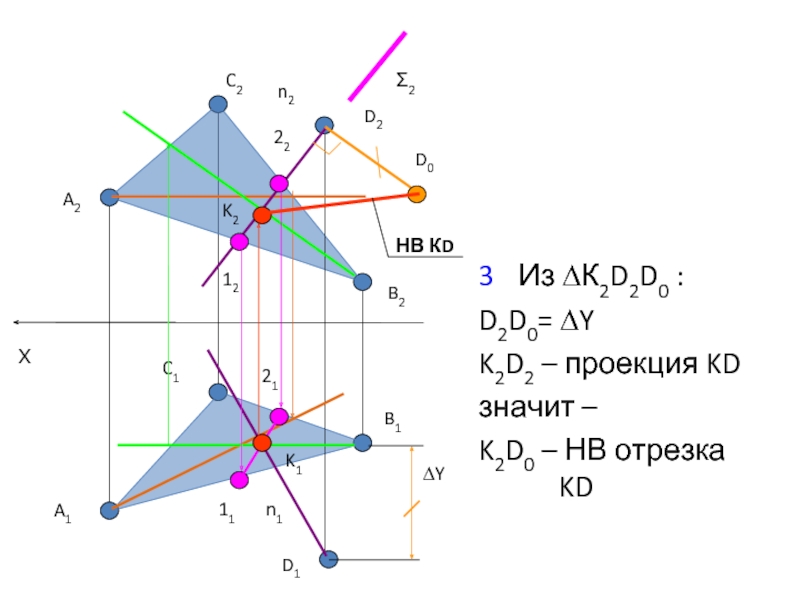
- 30. 3 Из ∆К2D2D0 : D2D0= ∆Y K2D2 –
- 31. Позиционные и метрические задачи Алгоритм решения: Определить
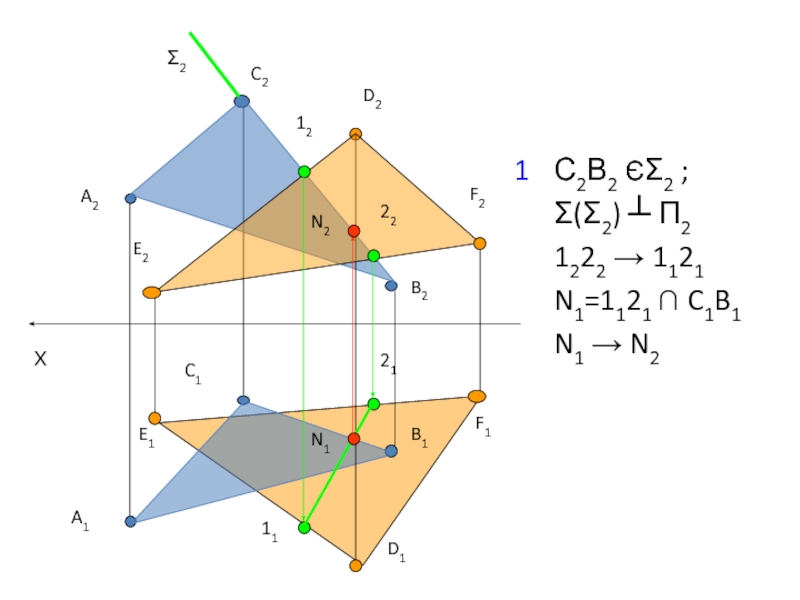
- 32. 1 С2В2 ЄΣ2 ; Σ(Σ2) ┴ П2
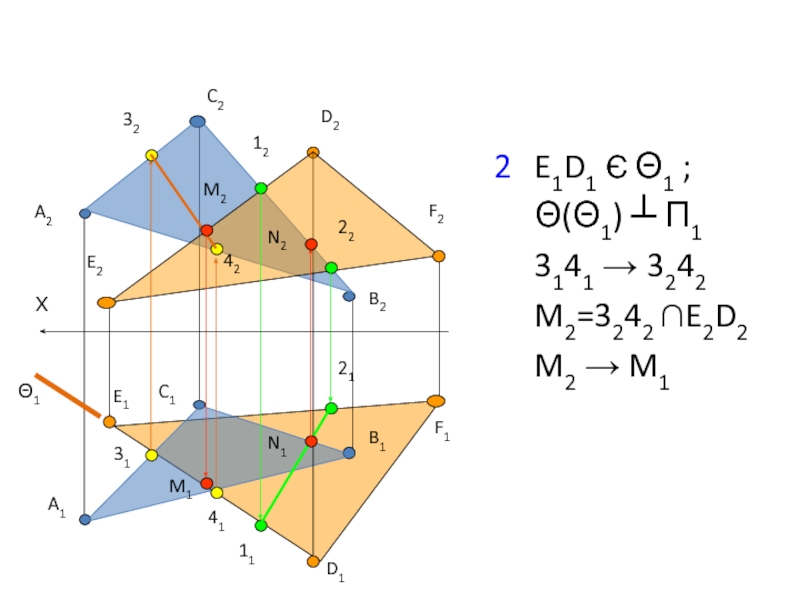
- 33. 2 E1D1 Є Θ1 ; Θ(Θ1) ┴ П1
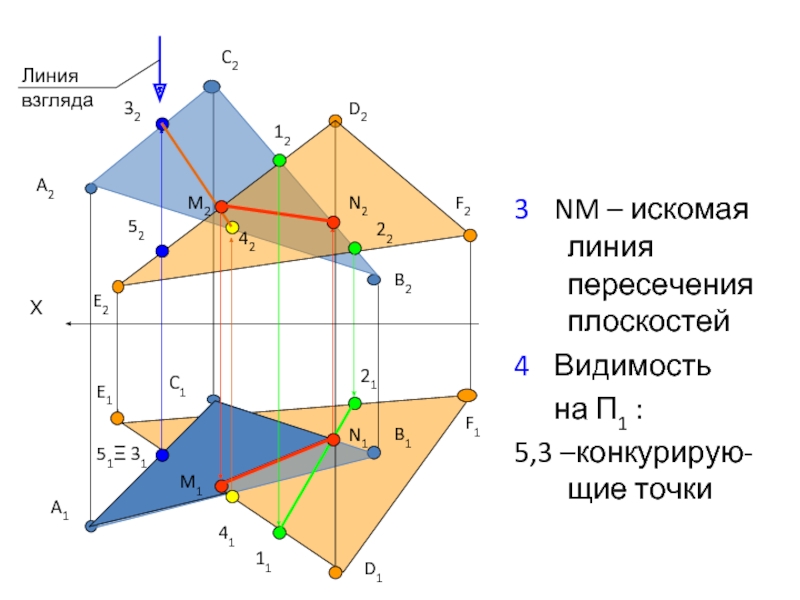
- 34. 3 NM – искомая линия пересечения плоскостей 4 Видимость на П1 : 5,3 –конкурирую-щие точки
- 35. Видимость на П1 : 1,6 –конкурирую-щие точки
План лекции Способы задания плоскостей Проецирование плоскости на плоскости проекций Взаимное положение точки и плоскости, прямой и плоскости, двух плоскостей Главные линии плоскости
Слайд 1Инженерная графика
Лекция 2. Плоскость.
Позиционные и метрические задачи
Лектор доцент, к.т.н. Алушкина
Слайд 2План лекции
Способы задания плоскостей
Проецирование плоскости на плоскости проекций
Взаимное положение точки и
плоскости, прямой и плоскости, двух плоскостей
Главные линии плоскости
Главные линии плоскости
Слайд 3Способы задания плоскостей
а) тремя точками, не лежащими на одной прямой
б) прямой
и точкой вне ее
в) двумя пересекающимися прямыми
г) двумя параллельными прямыми
д) плоской фигурой
е) следами е)
в) двумя пересекающимися прямыми
г) двумя параллельными прямыми
д) плоской фигурой
е) следами е)
Слайд 4Классификация плоскостей
Плоскости
Частного положения
Плоскости уровня
Проецирующие плоскости
Общего положения
Слайд 5Классификация плоскостей.
Плоскость общего положения
Плоскость общего положения – плоскость наклоненная ко всем
плоскостям проекций. Ни на одну из них не проецируется в натуральную величину.
Слайд 6Классификация плоскостей.
Плоскость уровня
Это плоскость, параллельная одной из плоскостей проекций
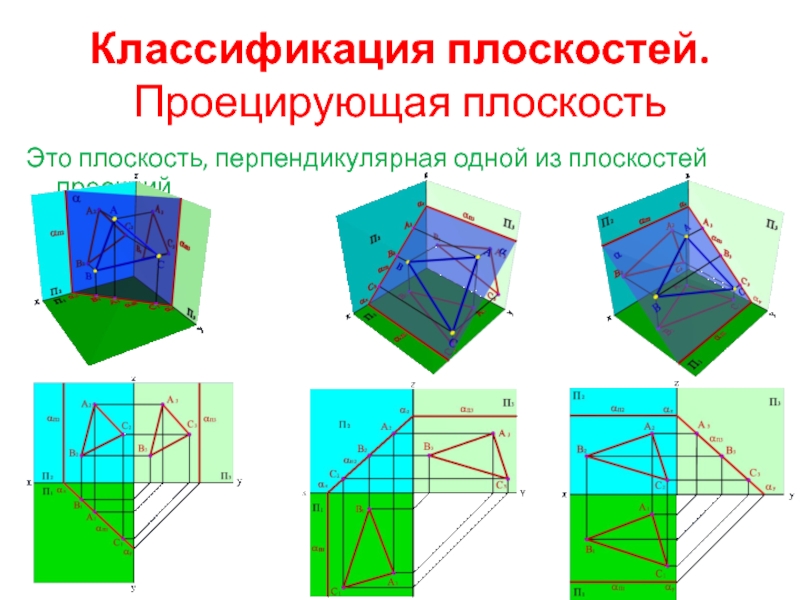
Слайд 7Классификация плоскостей.
Проецирующая плоскость
Это плоскость, перпендикулярная одной из плоскостей проекций
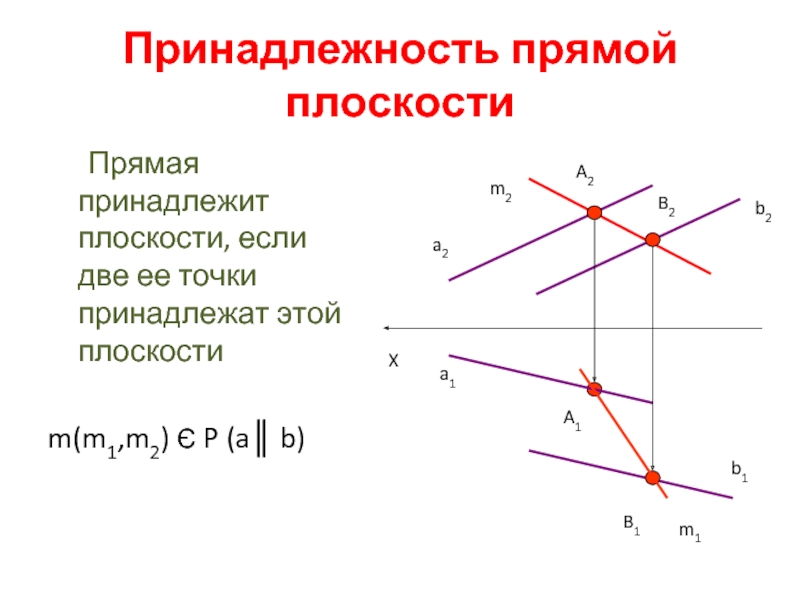
Слайд 8Принадлежность прямой плоскости
Прямая принадлежит плоскости, если две ее точки принадлежат этой
плоскости
m(m1,m2) Є P (a║ b)
m(m1,m2) Є P (a║ b)
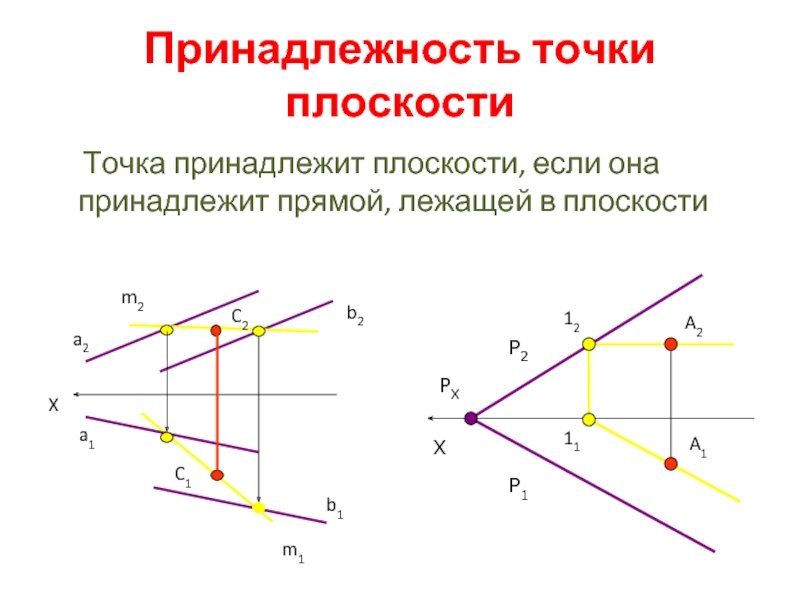
Слайд 9Принадлежность точки плоскости
Точка принадлежит плоскости, если она принадлежит
прямой, лежащей в плоскости
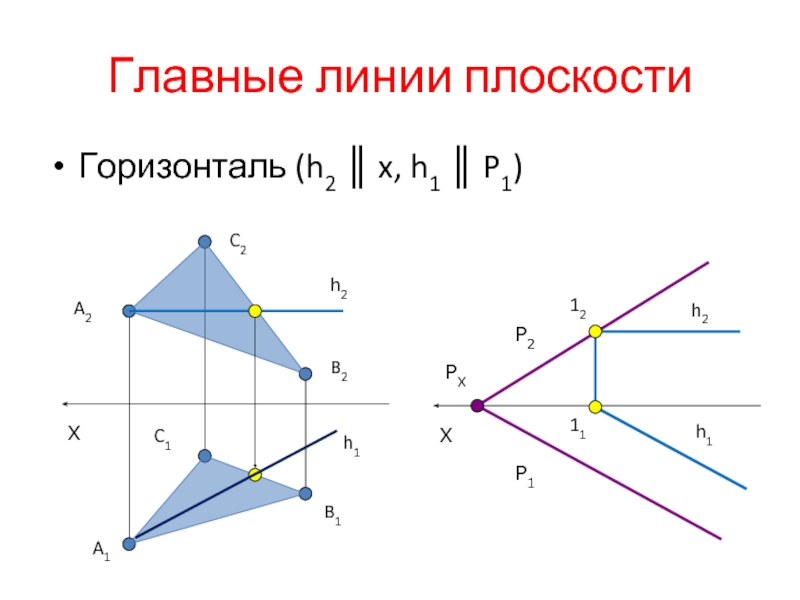
Слайд 13Главные линии плоскости
Линия ската – линия, перпендикулярная главной линии плоскости (горизонтали,
фронтали или профили) – n1 ┴ h1
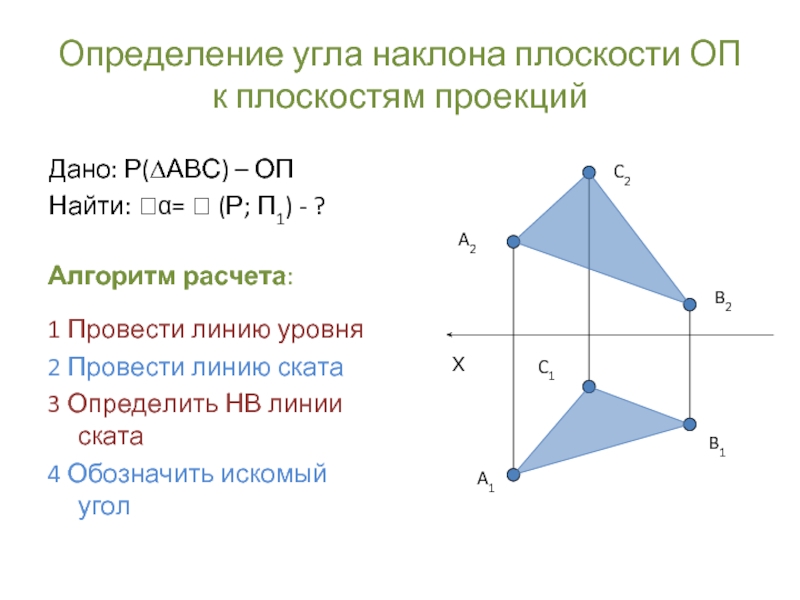
Слайд 14Определение угла наклона плоскости ОП к плоскостям проекций
Алгоритм расчета:
1 Провести линию
уровня
2 Провести линию ската
3 Определить НВ линии ската
4 Обозначить искомый угол
2 Провести линию ската
3 Определить НВ линии ската
4 Обозначить искомый угол
Дано: Р(∆АВС) – ОП
Найти: α= (Р; П1) - ?
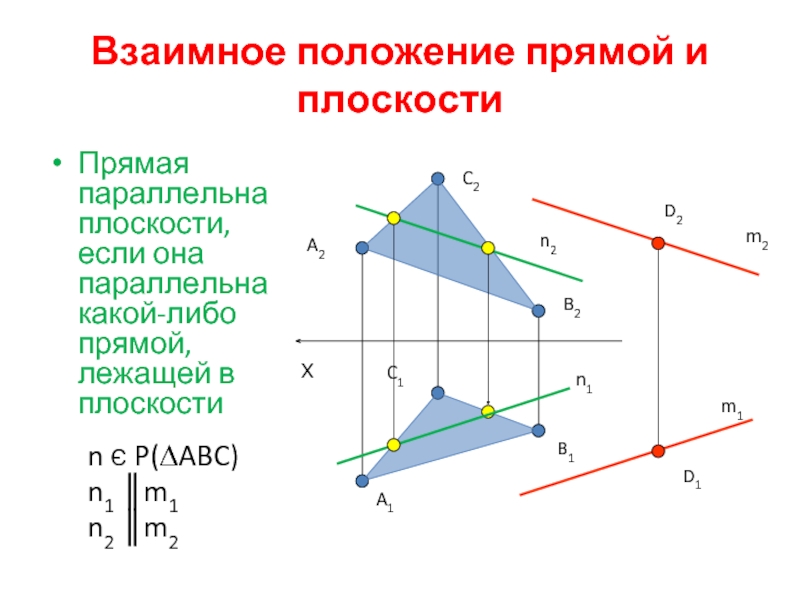
Слайд 17Взаимное положение прямой и плоскости
Прямая параллельна плоскости, если она параллельна какой-либо
прямой, лежащей в плоскости
n Є P(∆ABC)
n1 ║m1
n2 ║m2
n Є P(∆ABC)
n1 ║m1
n2 ║m2
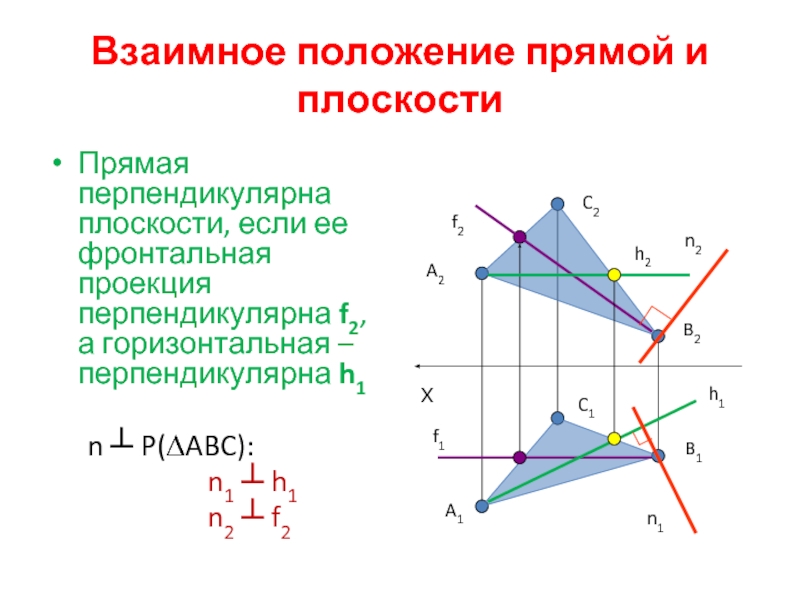
Слайд 18Взаимное положение прямой и плоскости
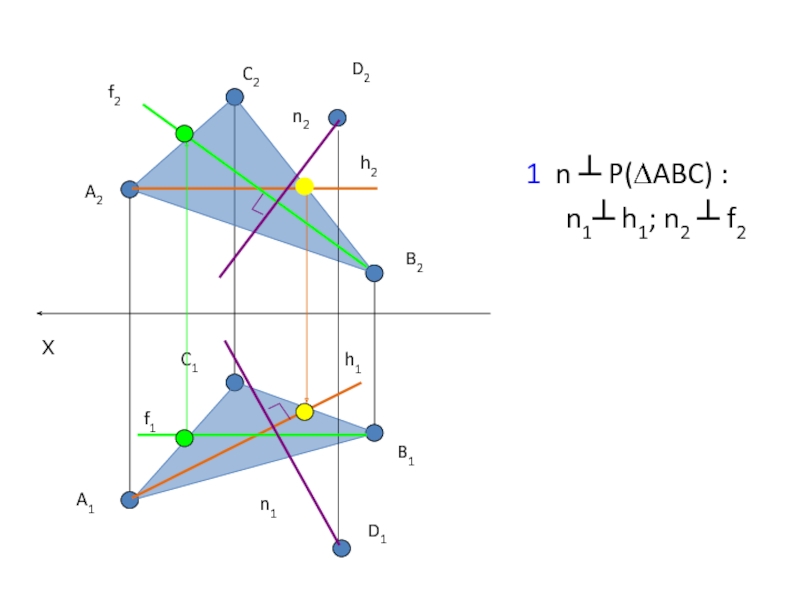
Прямая перпендикулярна плоскости, если ее фронтальная проекция
перпендикулярна f2, а горизонтальная – перпендикулярна h1
n ┴ P(∆ABC):
n1 ┴ h1
n2 ┴ f2
n ┴ P(∆ABC):
n1 ┴ h1
n2 ┴ f2
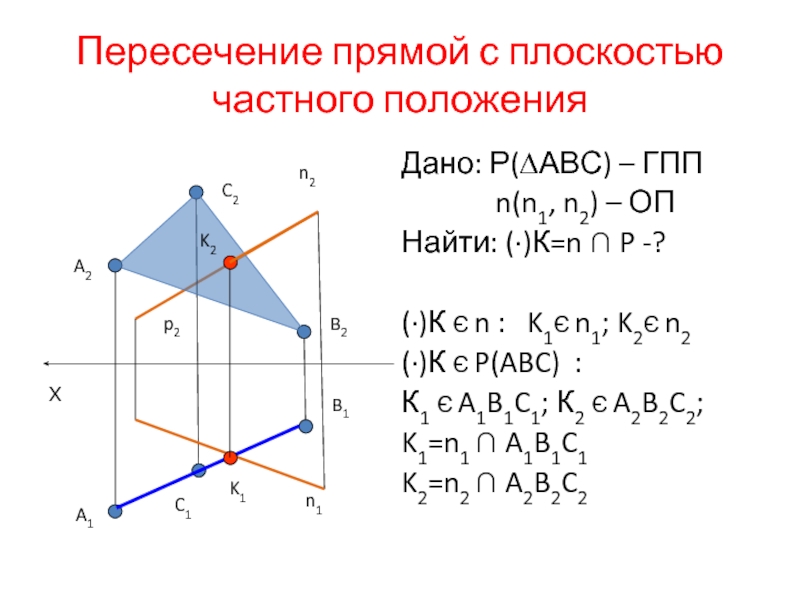
Слайд 19Пересечение прямой с плоскостью частного положения
Дано: Р(∆АВС) – ГПП
n(n1, n2)
– ОП
Найти: (·)К=n ∩ P -?
(·)К Є n : K1Є n1; K2Є n2
(·)К Є P(ABC) :
К1 Є A1B1C1; К2 Є A2B2C2;
K1=n1 ∩ A1B1C1
K2=n2 ∩ A2B2C2
Найти: (·)К=n ∩ P -?
(·)К Є n : K1Є n1; K2Є n2
(·)К Є P(ABC) :
К1 Є A1B1C1; К2 Є A2B2C2;
K1=n1 ∩ A1B1C1
K2=n2 ∩ A2B2C2
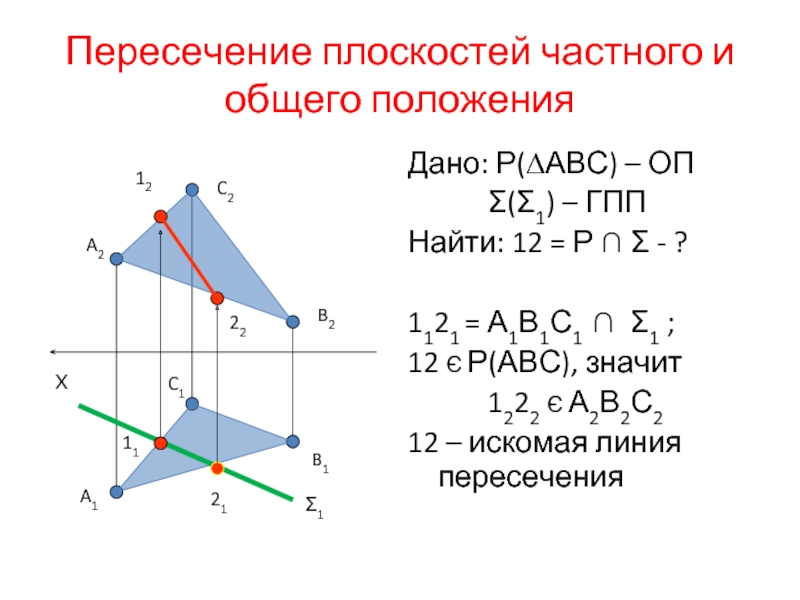
Слайд 20Пересечение плоскостей частного и общего положения
Дано: Р(∆АВС) – ОП
Σ(Σ1) – ГПП
Найти:
12 = Р ∩ Σ - ?
1121 = А1В1С1 ∩ Σ1 ;
12 Є Р(АВС), значит
1222 Є А2В2С2
12 – искомая линия пересечения
1121 = А1В1С1 ∩ Σ1 ;
12 Є Р(АВС), значит
1222 Є А2В2С2
12 – искомая линия пересечения
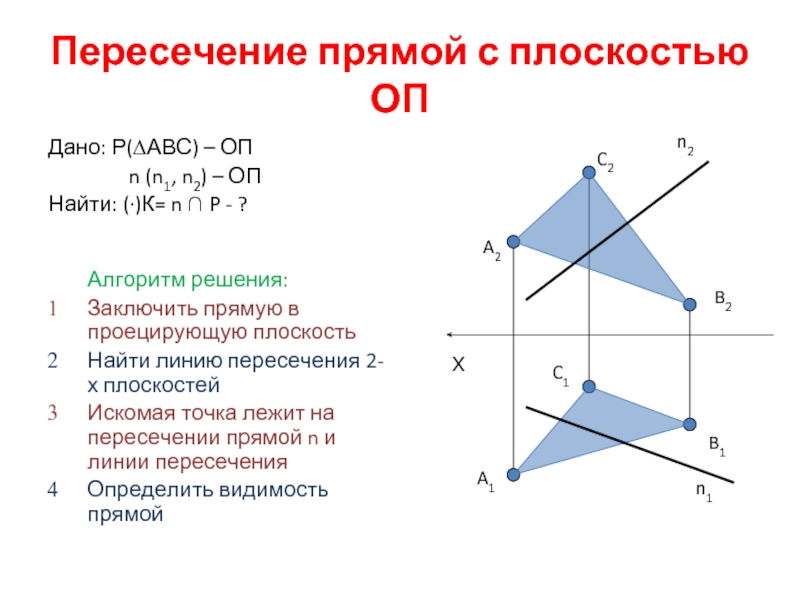
Слайд 21Пересечение прямой с плоскостью ОП
Алгоритм решения:
Заключить прямую в проецирующую плоскость
Найти линию
пересечения 2-х плоскостей
Искомая точка лежит на пересечении прямой n и линии пересечения
Определить видимость прямой
Искомая точка лежит на пересечении прямой n и линии пересечения
Определить видимость прямой
Дано: Р(∆АВС) – ОП
n (n1, n2) – ОП
Найти: (·)К= n ∩ P - ?
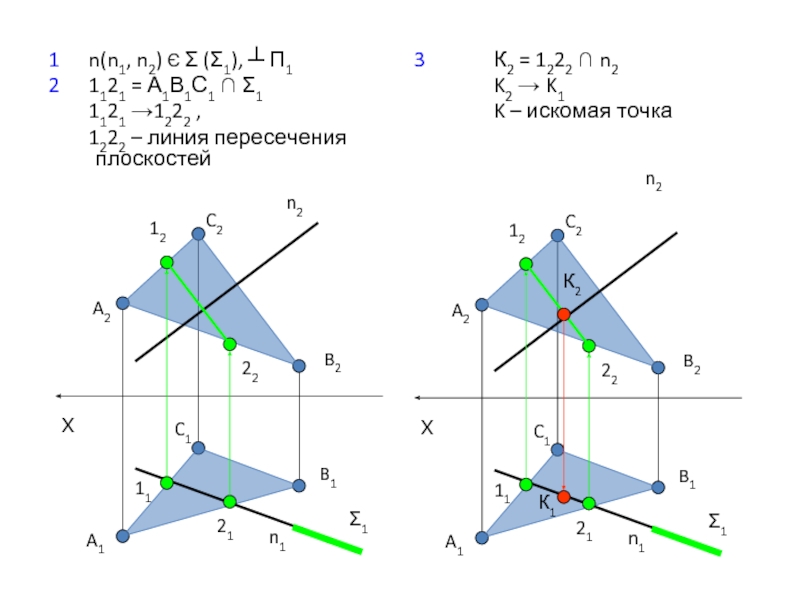
Слайд 221 n(n1, n2) Є Σ (Σ1), ┴ П1
2 1121 = А1В1С1
∩ Σ1
1121 →1222 ,
1222 – линия пересечения плоскостей
1121 →1222 ,
1222 – линия пересечения плоскостей
3 К2 = 1222 ∩ n2
K2 → K1
K – искомая точка
n2
Слайд 24Позиционные и метрические задачи
1 Определение расстояния от точки А(А1, А2)
до прямой m(m1, m2)
Алгоритм решения:
Через точку проводим плоскость, перпендикулярную прямой
Ищем точку пересечения прямой и плоскости
Определяем НВ отрезка
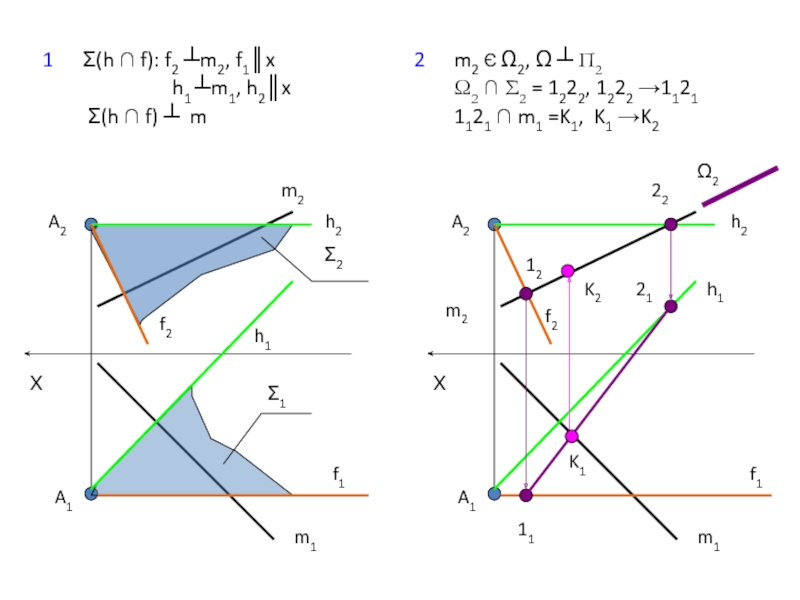
Слайд 251 Σ(h ∩ f): f2 ┴m2, f1║x
h1
┴m1, h2║x
Σ(h ∩ f) ┴ m
Σ(h ∩ f) ┴ m
2 m2 Є Ω2, Ω ┴ П2
Ω2 ∩ Σ2 = 1222, 1222 →1121
1121 ∩ m1 =K1, K1 →K2
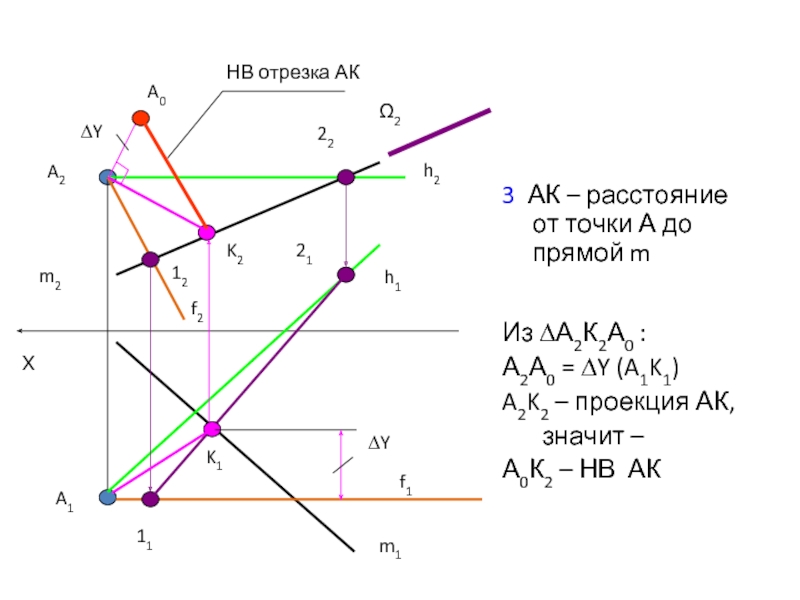
Слайд 263 АК – расстояние от точки А до прямой m
Из ∆А2К2А0
:
А2А0 = ∆Y (A1K1)
A2K2 – проекция АК,
значит –
А0К2 – НВ АК
А2А0 = ∆Y (A1K1)
A2K2 – проекция АК,
значит –
А0К2 – НВ АК
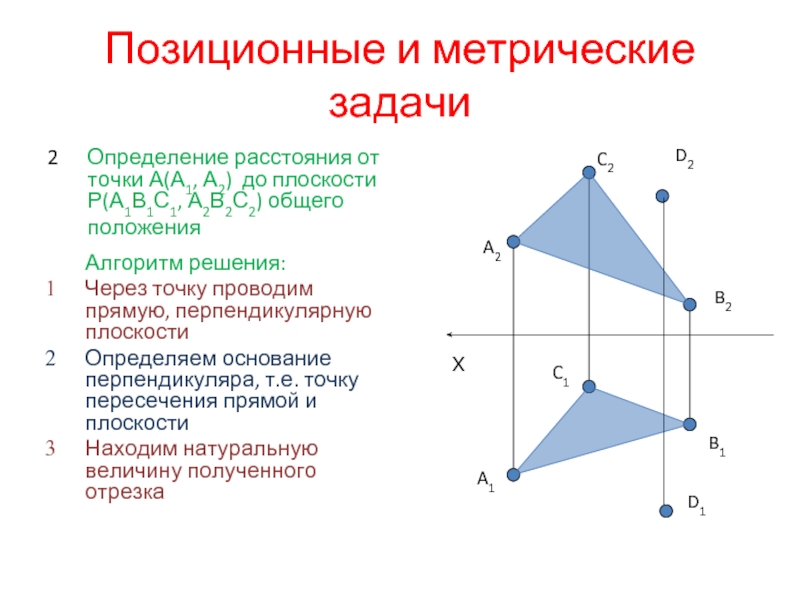
Слайд 27Позиционные и метрические задачи
2 Определение расстояния от точки А(А1, А2) до плоскости
Р(А1В1С1, А2В2С2) общего положения
Алгоритм решения:
Через точку проводим прямую, перпендикулярную плоскости
Определяем основание перпендикуляра, т.е. точку пересечения прямой и плоскости
Находим натуральную величину полученного отрезка
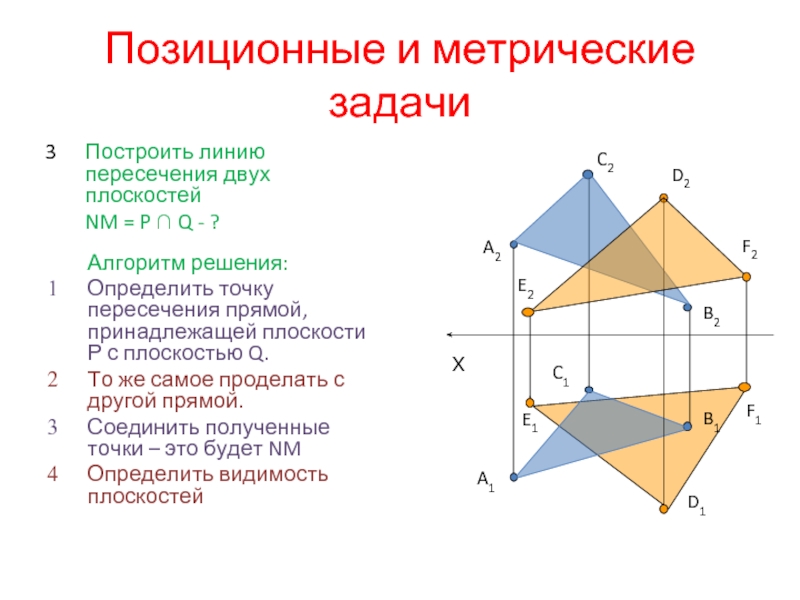
Слайд 31Позиционные и метрические задачи
Алгоритм решения:
Определить точку пересечения прямой, принадлежащей плоскости Р
с плоскостью Q.
То же самое проделать с другой прямой.
Соединить полученные точки – это будет NM
Определить видимость плоскостей
То же самое проделать с другой прямой.
Соединить полученные точки – это будет NM
Определить видимость плоскостей
3 Построить линию пересечения двух плоскостей
NM = P ∩ Q - ?
