- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Термодинамические свойства реальных газов (тема 7) презентация
Содержание
- 1. Термодинамические свойства реальных газов (тема 7)
- 2. МОЛЕКУЛЯРНАЯ ФИЗИКА ТЕРМОДИНАМИКА Т П У Сегодня *
- 3. Тема 7. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА РЕАЛЬНЫХ ГАЗОВ
- 4. 7.1. Реальные газы
- 5. Уравнение Менделеева – Клапейрона - самое простое,
- 6. Для газов с низкой температурой сжиже-ния (He,
- 7. Первая поправка в уравнении
- 8. При понижении температуры межмолекулярное взаимодействие в реальных
- 9. Наибольшее распространение вследствие простоты и физической
- 10. С учетом этих соображений уравнение состояния идеального
- 12. Помимо Нобелевской премии, Ван-дер-Ваальс получил почетную докторскую
- 13. Реальные газы – газы,
- 14. 7.2. Силы Ван-дер-Ваальса Я.Д. Ван-дер-Ваальс для
- 15. Межмолекулярные взаимодей-ствия имеют электрическую природу
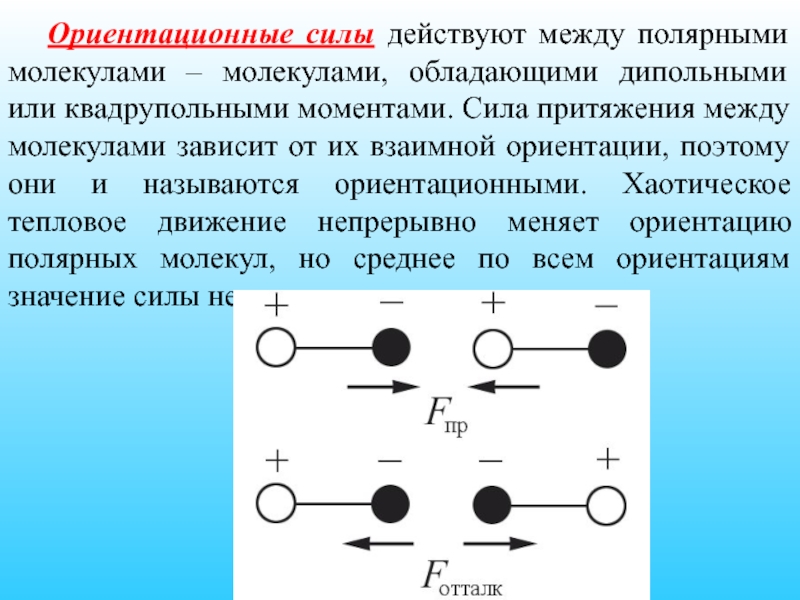
- 16. Ориентационные силы действуют между полярными молекулами –
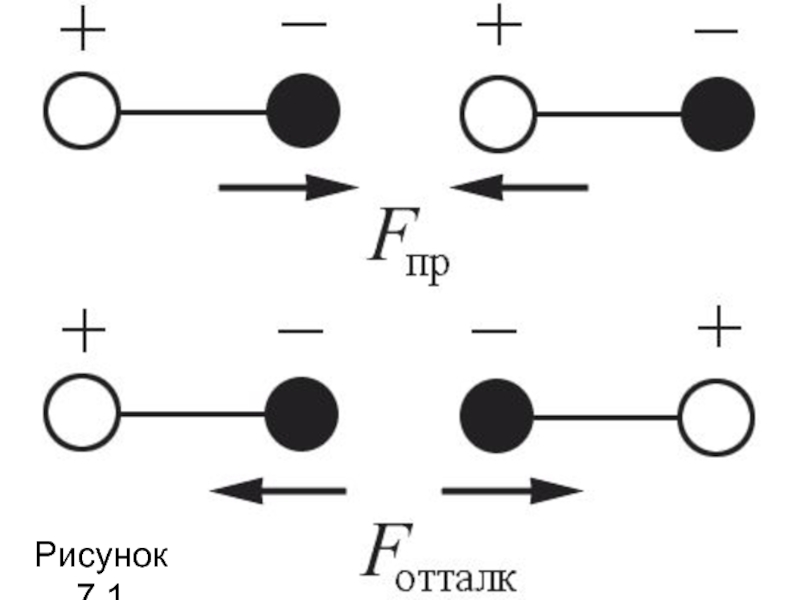
- 17. Рисунок 7.1
- 18. Среднее значение потенциальной энергии ориентационного межмолекулярного взаимодействия
- 19. Индукционные (поляризационные) силы действуют между полярной и
- 20. Дисперсионное молекулярное взаимодействие возникает благодаря
- 21. Данное взаимодействие называется дисперсионным, его энергия определяется
- 22. Отметим, что все три силы и энергии
- 23. Силы отталкивания действуют между молекулами на очень
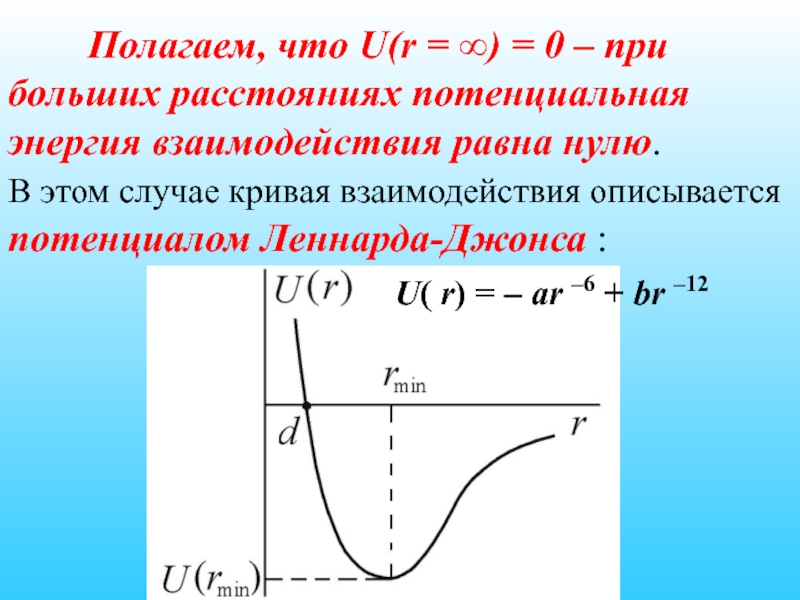
- 24. Полагаем, что U(r = ∞) = 0
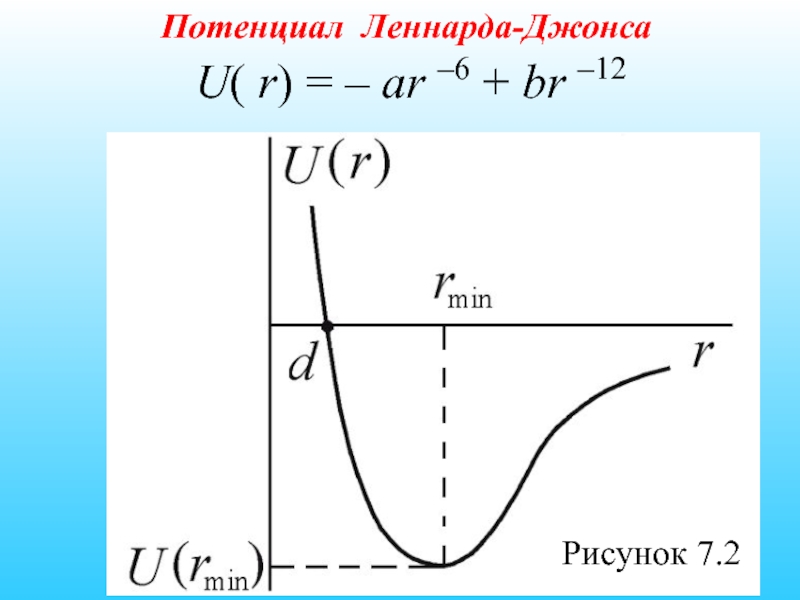
- 25. U( r) = – ar –6 + br –12 Рисунок 7.2 Потенциал Леннарда-Джонса
- 26. Глубина потенциала равна U(rmin) = –a2/4b при
- 27. 7.3. Вывод уравнения Ван-дер-Ваальса
- 28. Учтем влияние конечных размеров молекул
- 29. В результате в сосуде, содержащем N молекул
- 30. Объем, доступный точечным молекулам, будет равен
- 31. Для ν = m/μ молей газа уравнение
- 32. Рассмотрим влияние сил притяжения на
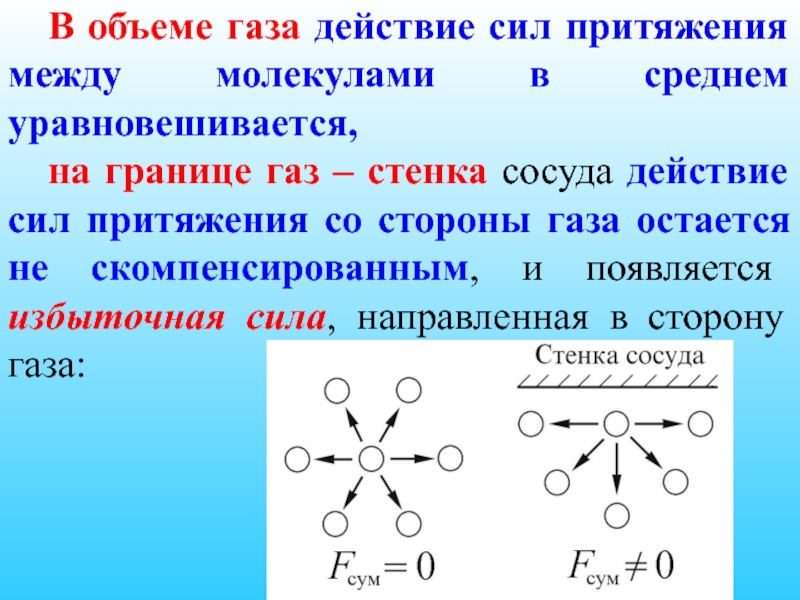
- 33. В объеме газа действие сил притяжения между
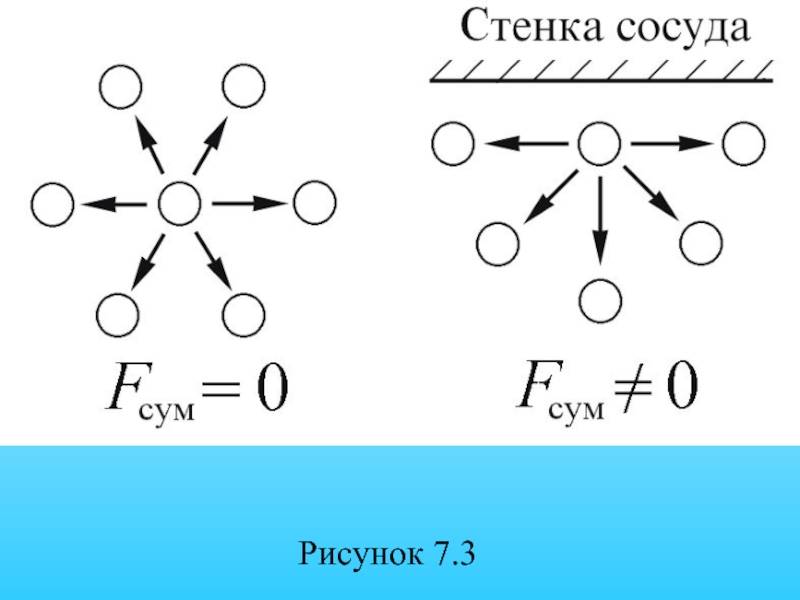
- 34. Рисунок 7.3
- 35. Дополнительное внутреннее давление пропорционально числу частиц, приходящихся
- 36. Избыточное внутреннее давление Pi
- 37. С учетом внутреннего давления уравнение состояния примет
- 38. Учитывая совместное действие сил притяжения и
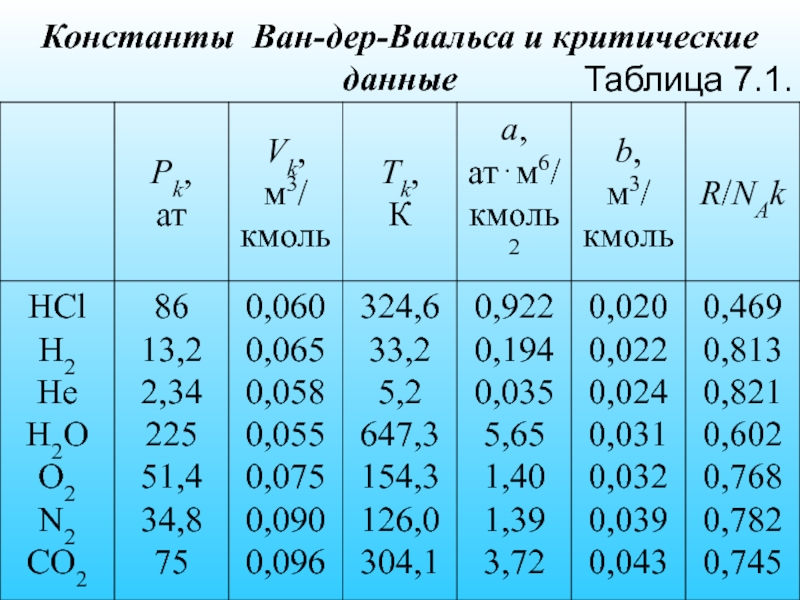
- 39. Константы Ван-дер-Ваальса и критические данные Таблица 7.1.
- 40. Примечание. Константы а и b выбраны таким
- 41. 7.3. Изотермы уравнения Ван-дер-Ваальса Проанализируем изотермы уравнения
- 42. Поскольку данное уравнение имеет третью
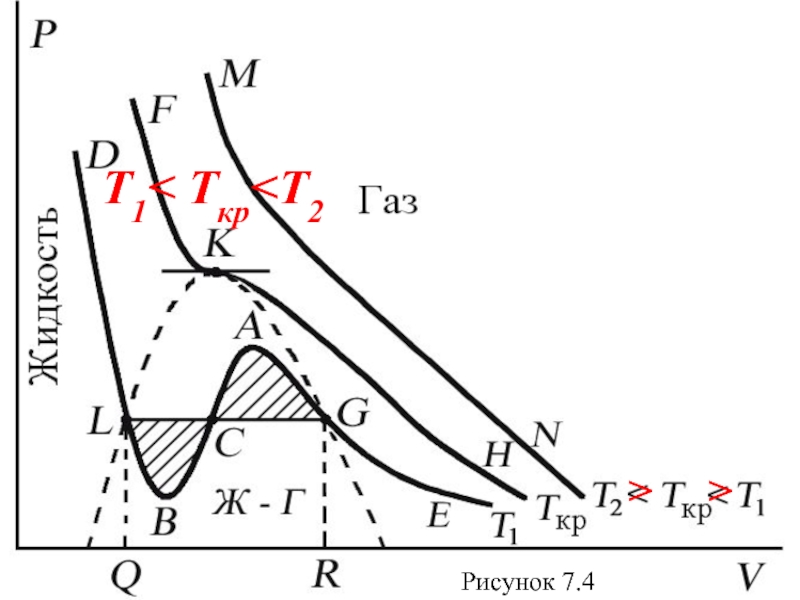
- 43. T1< Tкр > Рисунок 7.4
- 44. Изотерма при Ткр, которая разделяет
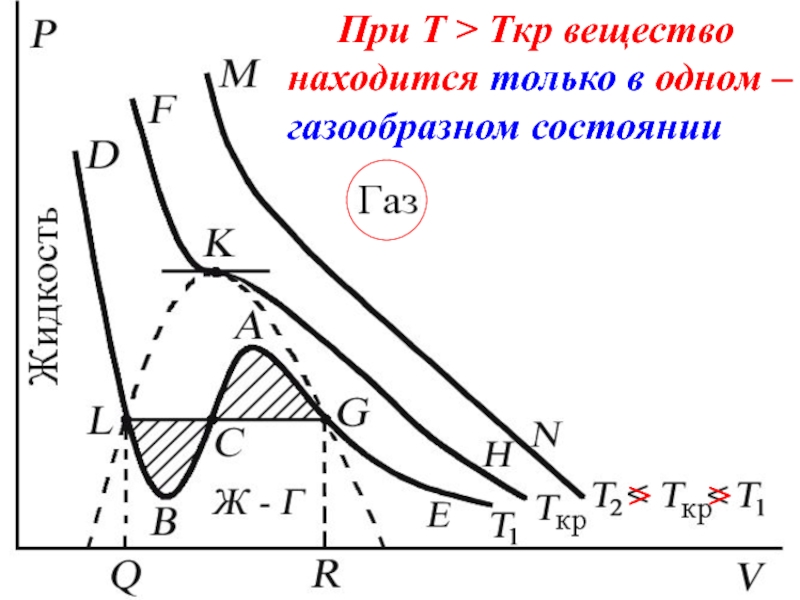
- 45. При T > Tкр
- 46. При температуре газа ниже критической
- 47. При температуре газа ниже
- 48. Поэтому область ВСА не может
- 49. Система переходит из области устойчивых состояний GE
- 50. При квазистатическом сжатии, начиная с
- 51. Наличие критической точки на изотерме Ван-дер-Ваальса означает,
- 52. Такую температуру Менделеев назвал температурой абсолютного кипения.
- 53. Критическая точка K - точка
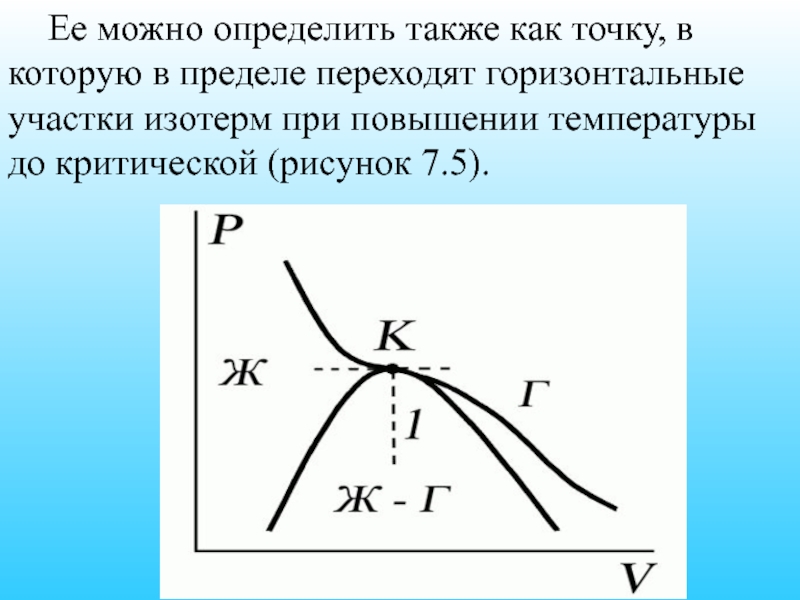
- 54. Ее можно определить также как точку, в
- 55. На этом основан способ определения критических параметров Pk, Vk, Тk, (способ Эндрюса).
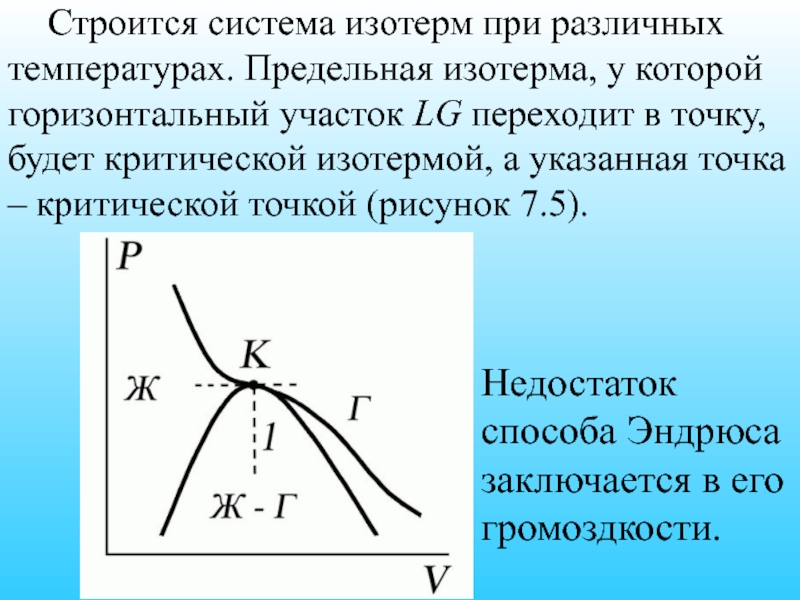
- 56. Строится система изотерм при различных
- 57. 7.4. Внутренняя энергия газа Ван-дер-Ваальса
- 58. Потенциальная энергия притяжения молекул равна работе, необходимой
- 59. Дополнительное давление газа Ван-дер-Ваальса за счет взаимного
- 60. Полная энергия одного моля газа Ван-дер-Ваальса :
- 61. Принципиальное значение уравнения Ван-дер-Ваальса определяется
- 62. 2) Уравнение долго рассматривалось как некоторый
- 63. Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию
- 64. Две модификации уравнения предложил Клаузиус, и обе
- 65. Выяснилось, что ни одно из уравнений состояния,
- 66. Если идеальный газ адиабатно расширяется и совершает
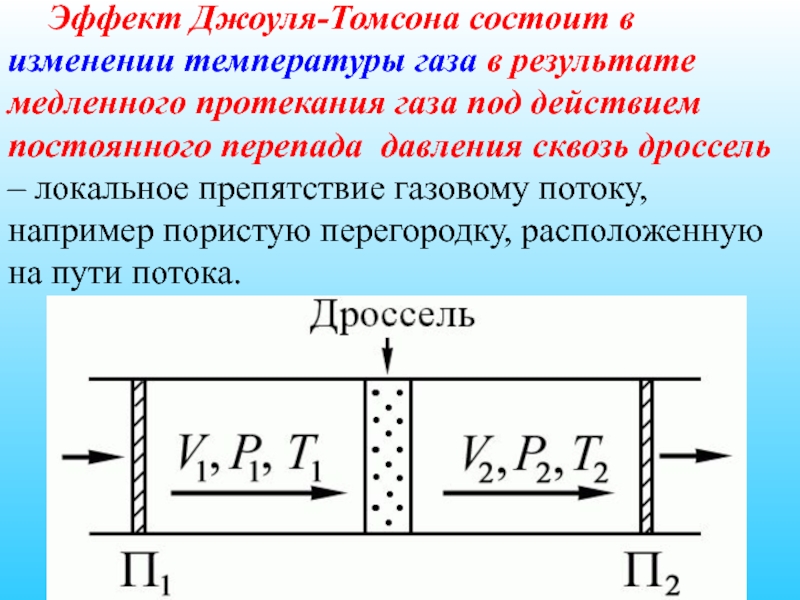
- 67. Эффект Джоуля-Томсона состоит в изменении температуры газа
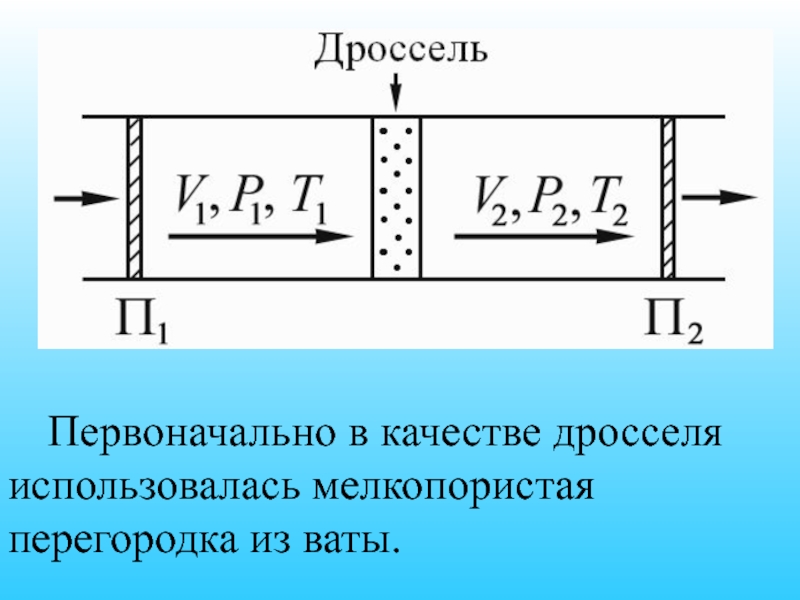
- 68. Первоначально в качестве дросселя использовалась мелкопористая перегородка из ваты.
- 69. Эффект Джоуля-Томсона свидетельствует о наличии в газе
- 70. Совершенная над газом результирующая внешняя работа равна
- 71. Таким образом, в опыте Джоуля-Томсона сохраняется (остается
- 72. Эффект Джоуля-Томсона принято называть положительным, если газ
- 73. Превращение любого газа в жидкость – сжижение
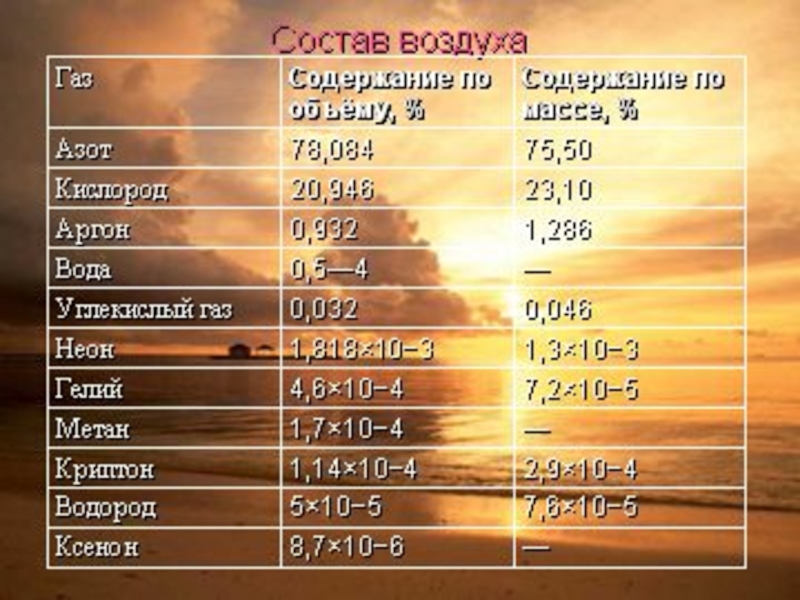
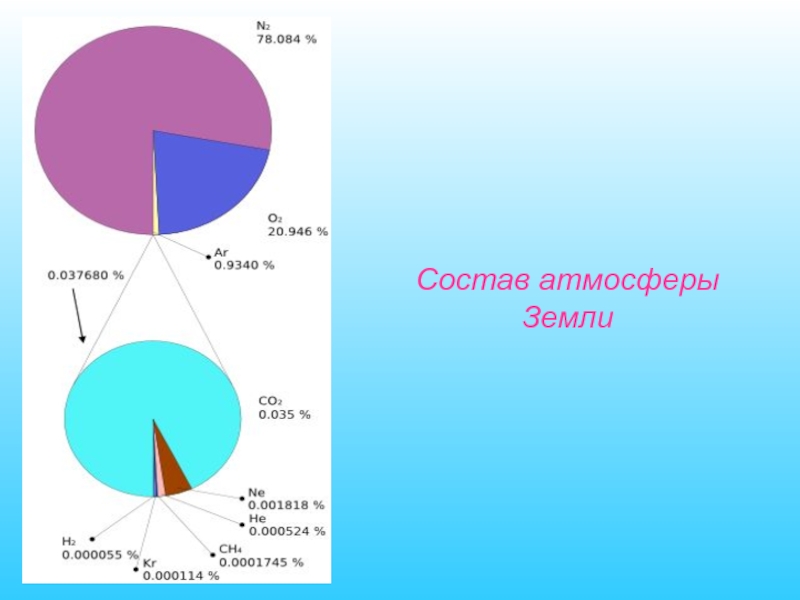
- 75. Состав атмосферы Земли
- 76. Схема установки для сжижения газов, в которой
- 77. Второй метод сжижения газов основан на охлаждении
- 78. Температуры до –261° С (12 К) и
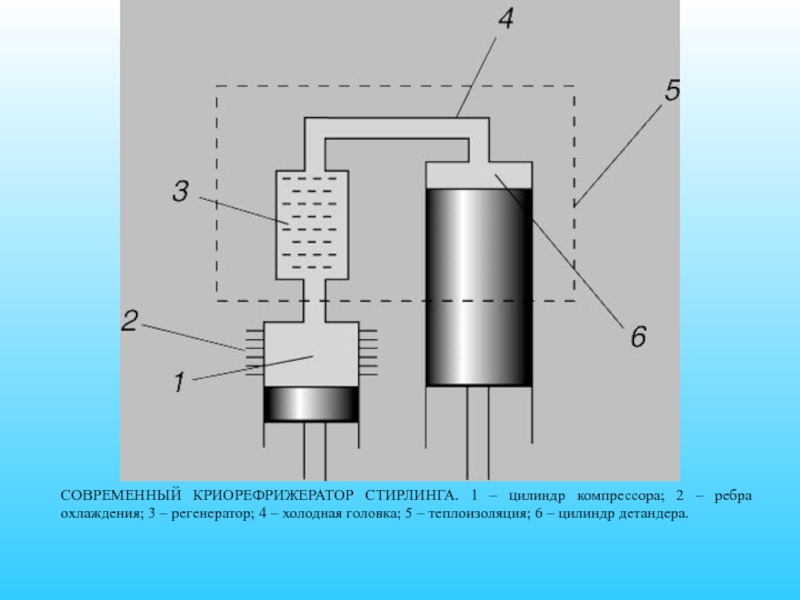
- 79. СОВРЕМЕННЫЙ КРИОРЕФРИЖЕРАТОР СТИРЛИНГА. 1 – цилиндр компрессора;
- 81. Основные результаты Уравнение Ван-дер-Ваальса для
- 84. Лекция окончена !
Слайд 3Тема 7. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА РЕАЛЬНЫХ ГАЗОВ
7.1. Реальные газы
7.2. Вывод уравнения Ван-дер-Ваальса
7.3. Изотермы уравнения
Ван-дер-Ваальса
7.4. Внутренняя энергия газа
Ван-дер-Ваальса
7.5. Эффект Джоуля - Томпсона
Слайд 47.1. Реальные газы
Как известно, уравнение состояния устанавливает
или
Эта связь может выражаться не только в форме уравнения, но также графически или в виде таблиц, которые часто используются, особенно для практических целей.
Слайд 5 Уравнение Менделеева – Клапейрона - самое простое, надежное и известное уравнение
Слайд 6 Для газов с низкой температурой сжиже-ния (He, H2, Ne и даже
Слайд 7 Первая поправка в уравнении состояния идеального газа рассматривает
Слайд 8 При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации
Слайд 9 Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса
Слайд 10 С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение
Слайд 11
Слайд 12 Помимо Нобелевской премии, Ван-дер-Ваальс получил почетную докторскую степень Кембриджского университета. Кроме
Слайд 13 Реальные газы – газы, свойства которых зависят от
Слайд 147.2. Силы Ван-дер-Ваальса
Я.Д. Ван-дер-Ваальс для объяснения свойств реальных газов и
Слайд 15 Межмолекулярные взаимодей-ствия имеют электрическую природу и складываются из: сил
Слайд 16 Ориентационные силы действуют между полярными молекулами – молекулами, обладающими дипольными или
Слайд 18 Среднее значение потенциальной энергии ориентационного межмолекулярного взаимодействия равно
Слайд 19 Индукционные (поляризационные) силы действуют между полярной и неполярной молекулами, а также
Слайд 20 Дисперсионное молекулярное взаимодействие возникает благодаря виртуальному нарушению электронейтральности молекулы в
Слайд 21 Данное взаимодействие называется дисперсионным, его энергия определяется поляризуемостью молекул α1, α2:
Слайд 22 Отметим, что все три силы и энергии одинаковым образом убывают с
Слайд 23 Силы отталкивания действуют между молекулами на очень малых расстояниях, когда происходит
Слайд 24 Полагаем, что U(r = ∞) = 0 – при больших расстояниях
U( r) = – ar –6 + br –12
Слайд 26 Глубина потенциала равна U(rmin) = –a2/4b при rmin = (2b/a)1/6 –
Слайд 277.3. Вывод уравнения Ван-дер-Ваальса
Уравнение Ван-дер-Ваальса – одно из
Слайд 28 Учтем влияние конечных размеров молекул на уравнение состояния реального
Слайд 29 В результате в сосуде, содержащем N молекул конечных размеров, область объемом
Слайд 30 Объем, доступный точечным молекулам, будет равен V − b,
Слайд 31 Для ν = m/μ молей газа уравнение состояния газа с учетом
Слайд 32 Рассмотрим влияние сил притяжения на уравнение состояния идеального газа.
Слайд 33 В объеме газа действие сил притяжения между молекулами в среднем уравновешивается,
Слайд 35 Дополнительное внутреннее давление пропорционально числу частиц, приходящихся на единицу площади границы
Слайд 36 Избыточное внутреннее давление Pi (i − intrinsic) будет
Слайд 37 С учетом внутреннего давления уравнение состояния примет вид
Слайд 38 Учитывая совместное действие сил притяжения и сил отталкивания и полученные поправки
Слайд 40 Примечание. Константы а и b выбраны таким образом, чтобы получить оптимальное
Слайд 417.3. Изотермы уравнения Ван-дер-Ваальса
Проанализируем изотермы уравнения Ван-дер-Ваальса – зависимости Р от
(P + ν2 a/V 2)(V − νb) = νRT.
Умножив уравнение Ван-дер-Ваальса на V 2 и раскрыв скобки, получим:
PV 3 – (RT + bP) νV 2 + aν2V − abν3= 0
Слайд 42 Поскольку данное уравнение имеет третью степень относительно V, а
Слайд 44 Изотерма при Ткр, которая разделяет немонотонные T < Tкр
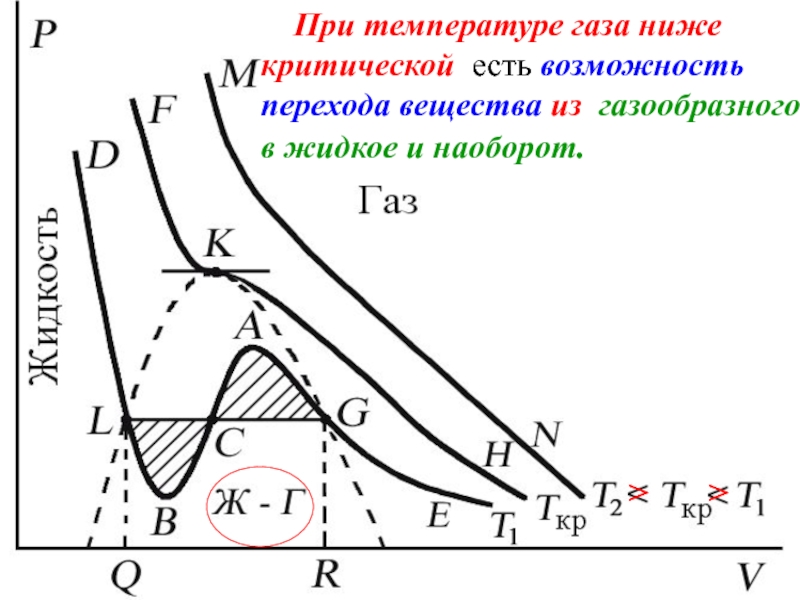
Слайд 46 При температуре газа ниже критической есть возможность перехода вещества
Слайд 47 При температуре газа ниже критической есть возможность перехода
>
>
Слайд 48 Поэтому область ВСА не может устойчиво существовать. В областях
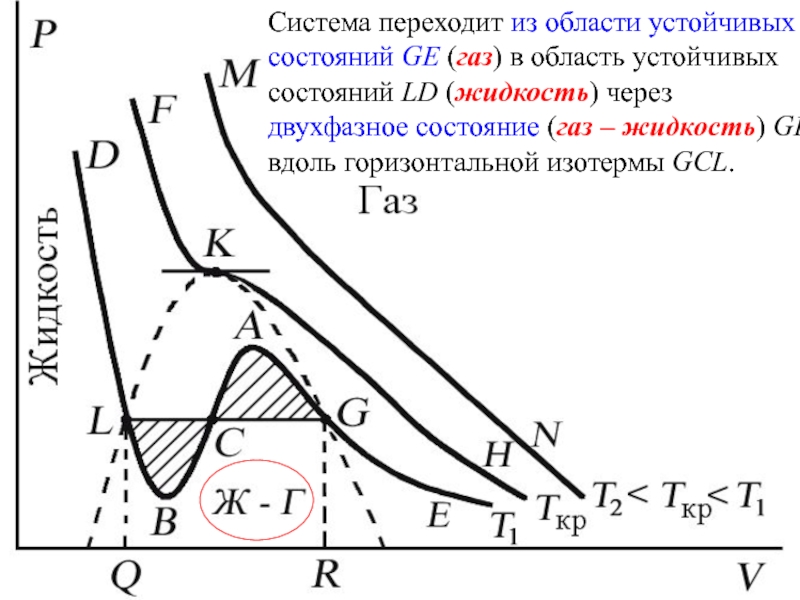
Слайд 49Система переходит из области устойчивых состояний GE (газ) в область устойчивых
Слайд 50 При квазистатическом сжатии, начиная с точки G, система распадается
Слайд 51 Наличие критической точки на изотерме Ван-дер-Ваальса означает, что для каждой жидкости
Слайд 52 Такую температуру Менделеев назвал температурой абсолютного кипения. Выше этой температуры, согласно
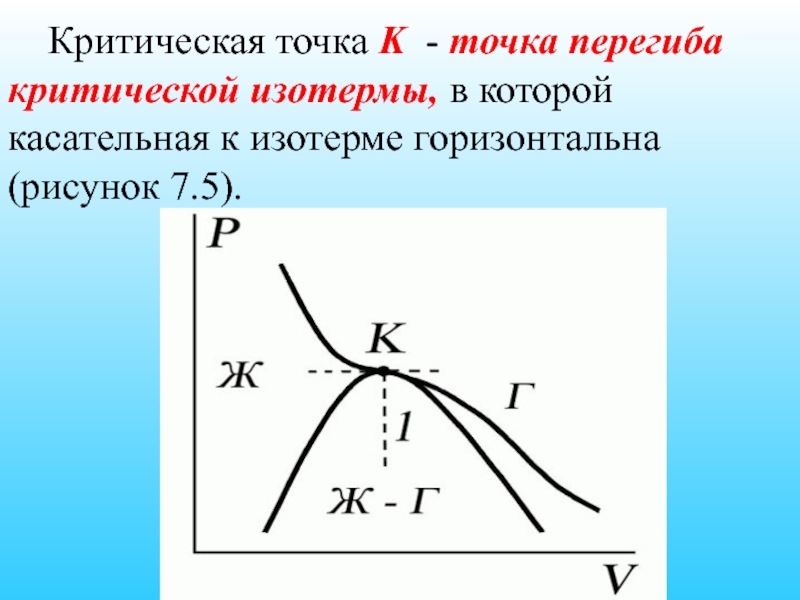
Слайд 53 Критическая точка K - точка перегиба критической изотермы, в
Слайд 54 Ее можно определить также как точку, в которую в пределе переходят
Слайд 56 Строится система изотерм при различных температурах. Предельная изотерма, у
Недостаток способа Эндрюса заключается в его громоздкости.
Слайд 577.4. Внутренняя энергия газа Ван-дер-Ваальса
Энергия одного моля газа
внутренней энергии молекул газа;
кинетической энергии теплового движения центра масс молекул
потенциальной энергии взаимного притяжения молекул
Слайд 58 Потенциальная энергия притяжения молекул равна работе, необходимой для разведения молекул на
Слайд 59 Дополнительное давление газа Ван-дер-Ваальса за счет взаимного притяжения молекул равно a/Vm2,
Vm – молярный объем: Vm = V/ν, ν = m/μ.
Знак «минус» указывает на то, что между молекулами действуют силы притяжения.
Слайд 60 Полная энергия одного моля газа Ван-дер-Ваальса :
Если СV не зависит от
Слайд 61 Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами: 1) Уравнение было
Слайд 62 2) Уравнение долго рассматривалось как некоторый общий вид уравнения состояния
Слайд 63 Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе,
Слайд 64 Две модификации уравнения предложил Клаузиус, и обе они связаны с усложнением
Слайд 65 Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных
Слайд 66 Если идеальный газ адиабатно расширяется и совершает при этом работу, то
Подобный процесс, но с реальным газом – адиабатное расширение реального газа с совершением внешними силами положительной работы – осуществили английские физики Дж.Джоуль и У.Томсон (лорд Кельвин) в 1865г.
Эффект Джоуля-Томсона
Слайд 67 Эффект Джоуля-Томсона состоит в изменении температуры газа в результате медленного протекания
Слайд 69 Эффект Джоуля-Томсона свидетельствует о наличии в газе сил межмолекулярного взаимодействия. Газ совершает
Слайд 70 Совершенная над газом результирующая внешняя работа равна В адиабатических внешних условиях эта
Слайд 71 Таким образом, в опыте Джоуля-Томсона сохраняется (остается неизменной) величина
Энтальпия – термодинамический потенциал характеризующий состояние системы в равновесии при выборе в качестве независимых переменных энтропии S и давления P
Полный дифференциал имеет вид:
dH= VdР + TdS
Слайд 72 Эффект Джоуля-Томсона принято называть положительным, если газ в процессе дросселирования охлаждается
Слайд 73 Превращение любого газа в жидкость – сжижение газа – возможно лишь
Критические температуры
Сжижение газов
Слайд 76 Схема установки для сжижения газов, в которой используется эффект Джоуля-Томсона –
Слайд 77 Второй метод сжижения газов основан на охлаждении газа при совершении им
Слайд 78Температуры до –261° С (12 К) и ниже можно также получать
Слайд 79СОВРЕМЕННЫЙ КРИОРЕФРИЖЕРАТОР СТИРЛИНГА. 1 – цилиндр компрессора; 2 – ребра охлаждения;
Слайд 81Основные результаты
Уравнение Ван-дер-Ваальса для произвольного количества вещества ν реального
где а и b – постоянные Ван-дер-Ваальса
V – объем, занимаемый газом;
P – давление газа на стенки сосуда.