- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Работа и энергия. Закон сохранения энергии в механике презентация
Содержание
- 1. Работа и энергия. Закон сохранения энергии в механике
- 2. Механическая работа – скалярная
- 3. 1) Работа силы упругости
- 4. Мощность Мощность - скалярная физическая величина, характеризующая
- 5. Энергия Энергия –
- 6. Механическая энергия –
- 7. Кинетическая энергия
- 8. Потенциальная энергия Потенциальная
- 9. Потенциальная энергия тела
- 10. Изменение потенциальной энергии
- 11. Связь консервативной силы с потенциальной энергией
- 12. Закон сохранения энергии в механике
- 13. Закон сохранения механической энергии
- 14. Закон сохранения механической энергии
- 15. Устойчивость равновесия
- 16. Особенности классической механики - Всеобщность законов
Слайд 1Работа и энергия.
Закон сохранения энергии в механике
Механическая работа
Мощность
Энергия. Механическая энергия.
Закон сохранения энергии в механике
Слайд 2
Механическая работа – скалярная физическая величина, характеризующая движение тела под действием
Элементарная работа:
Механическая работа
На основе III закона Ньютона работа силы и работа против силы противоположны по знаку:
Работа численно равна площади под графиком проекции силы на направление перемещения:
Знак работы:
Работа при перемещении 1-2 :
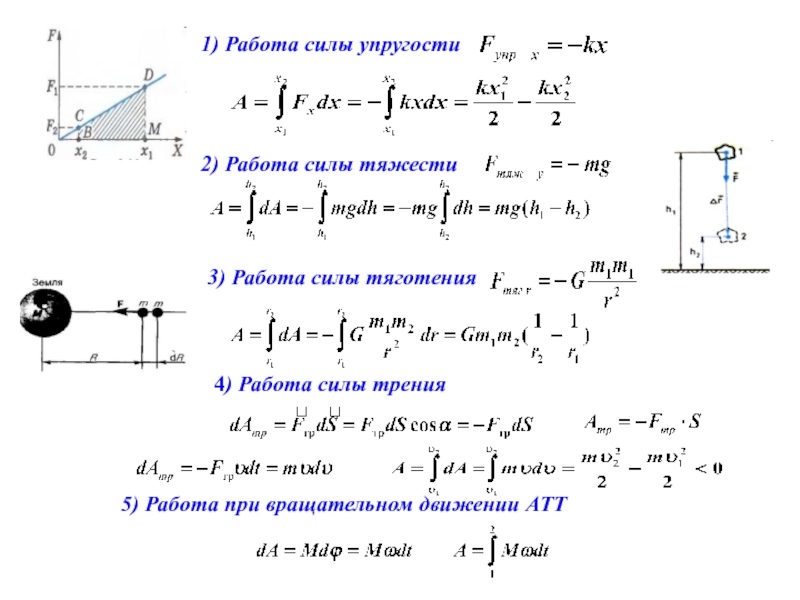
Слайд 3
1) Работа силы упругости
2) Работа силы тяжести
4) Работа силы трения
5) Работа
3) Работа силы тяготения
Слайд 4Мощность
Мощность - скалярная физическая величина, характеризующая быстроту совершения работы и равная
Средняя мощность определяется отношением работы ко времени, за которое она была совершена:
Мгновенная мощность равна производной от величины работы по времени:
При известной мощности работа определяется выражениями:
Слайд 5Энергия
Энергия – скалярная физическая величина, являющаяся единой мерой различных форм движения
Формам движения материи соответствуют виды энергии:
Механическая
Внутренняя (тепловая)
Электромагнитная
Ядерная….
Энергия – конечная, однозначная, непрерывная, аддитивная функция параметров состояния системы.
Закон сохранения энергии: в замкнутой системе тел энергия может переходить от одних тел к другим, превращаться из одних видов в другие, но её суммарное значение остаётся неизменным.
Слайд 6
Механическая энергия – скалярная физическая величина, мера механического движения тела, изменение
Механическая энергия (W) - функция параметров механического состояния:
Различают: кинетическую, обусловленную движением, и потенциальную, связанную с взаимодействием,
составляющие механической энергии.
Механическая энергия
Слайд 7Кинетическая энергия
Кинетическая энергия, Wкин (V),- часть механической энергии, обусловленная движением тела
скорости (импульса).
Теорема об изменении кинетической энергии:
Изменение кинетической энергии тела равно работе равнодействующей всех сил, приложенных к телу.
Поступательное движение
Вращательное движение
Особенности кинетической энергии:
положительность, аддитивность, относительность.
Слайд 8Потенциальная энергия
Потенциальная энергия, Wпот (r), – часть механической энергии, обусловленная взаимодействием
Особенности потенциальной энергии:
-может быть как положительна, так и отрицательна,
-её численное значение зависит от выбора нулевого уровня,
- расчётная формула определяется характером взаимодействия.
Слайд 9Потенциальная энергия тела
2. Потенциальная энергия тела в поле силы тяжести
3.Потенциальная энергия
1.Потенциальная энергия при действии силы упругости
Слайд 10Изменение потенциальной энергии
Работа консервативной силы равна убыли потенциальной энергии.
Потенциальную энергию
С потенциальным полем связаны консервативные силы, зависящие от положения тел, , работа которых не зависит от формы траектории, а определяется лишь начальным и конечным положением тела в потенциальном поле.
Работа консервативной силы при перемещения тела по замкнутой траектории
равна нулю.
Консервативные силы: тяжести, тяготения, упругости, электростатические силы...
Слайд 11Связь консервативной силы с потенциальной энергией
Градиент функции– вектор, характеризующий быстроту
Выразим работу потенциальной силы через убыль потенциальной энергии:
Полный дифференциал функции трёх переменных dWx,y,z :
Видим, что проекции вектора силы на координатные оси равны соответствующим частным производным от потенциальной энергии тела с противоположным знаком:
Вектор силы
Действующая на тело в потенциальном поле сила равна по модулю и противоположна по направлению градиенту потенциальной энергии тела.
Слайд 12Закон сохранения энергии в механике
Изменение механической энергии системы тел определяется работой
Изменение полной механической энергии системы равно алгебраической сумме работ всех неконсервативных и внешних сил, действующих на тела системы.
Закон сохранения энергии в механике: полная механическая энергия замкнутой консервативной системы тел есть величина постоянная.
Слайд 13Закон сохранения механической энергии
Пример 1. Свободное падение- движение под действием силы
Пример 2. Абсолютно упругий удар- удар, при котором сохраняется механическая энергия системы:
Закон сохранения энергии
Закон сохранения импульса
Слайд 14Закон сохранения механической энергии
Потенциальная яма:
условием W > U0 движение ограничено областью
Частица с энергией ε < U0 может находиться только в области 0 < x < a.
В области В-С при полной энергии частицы W= Е1 величина потенциальной энергии U больше полной энергии (U > Е1), частица с такой энергией не может преодолеть потенциальный барьер, её движение ограничено областью А-В.
Потенциальный барьер:
Любая механическая система стремится к состоянию с минимальной энергией.
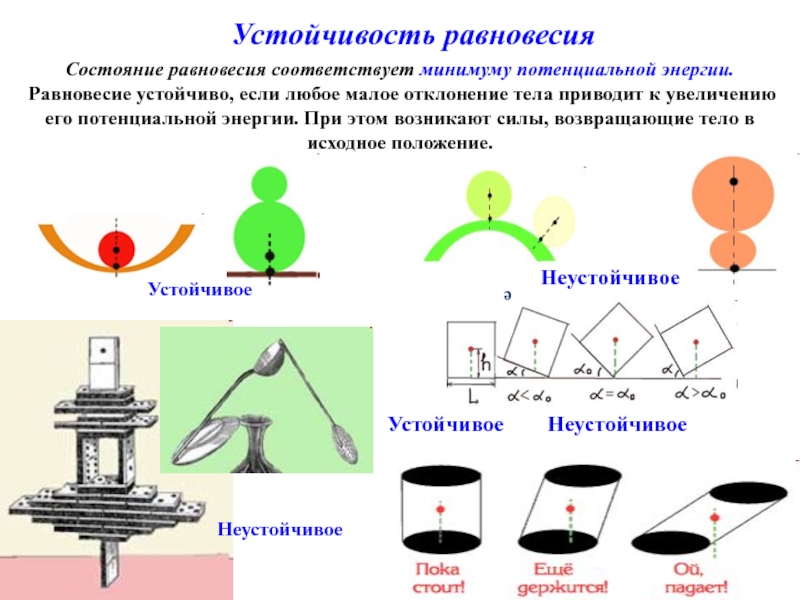
Слайд 15Устойчивость равновесия
Устойчивое
Устойчивое
е
Неустойчивое
Неустойчивое
Неустойчивое
Состояние равновесия соответствует минимуму потенциальной энергии.
Равновесие устойчиво, если любое
Слайд 16 Особенности классической механики
- Всеобщность законов движения в природе
- Задание начальных
движения однозначно определяет все
последующие состояния. Вселенная- гигантский детерминированный механизм.
- Движение обратимо
- Принцип дальнодействия
- Механицизм и редукционизм
- Корпускулярная модель реальности
- Абсолютность свойств пространства и
времени. Их независимость
- Основа технической революции