- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория электрических цепей презентация
Содержание
- 1. Теория электрических цепей
- 2. Лекция №7
- 3. Учебные вопросы 1. Резонанс в последовательном колебательном
- 4. Литература Попов В.П. Основы теории цепей:
- 5. Режимы работы последовательной RLC-цепи
- 6. Свойства активно-индуктивного режима последовательной RLC-цепи
- 7. Свойства активно-ёмкостного режима последовательной RLC-цепи
- 8. Свойства режима резонанса напряжений последовательной RLC-цепи
- 9. Резонансом называется режим работы электрической цепи, содержащей
- 10. РЕЗОНАНС В ПОСЛЕДОВАТЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ Основным
- 11. Характеристики резонанса напряжений 1. Резонансная частота:
- 12. Способы возбуждения резонанса 1 способ. При неизменных
- 18. Физический смысл добротности контура
- 20. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА
- 21. Амплитудно-частотные характеристики
- 22. 1. В дорезонансной области при ω
- 23. Расстройки колебательных контуров Абсолютная расстройка – разность
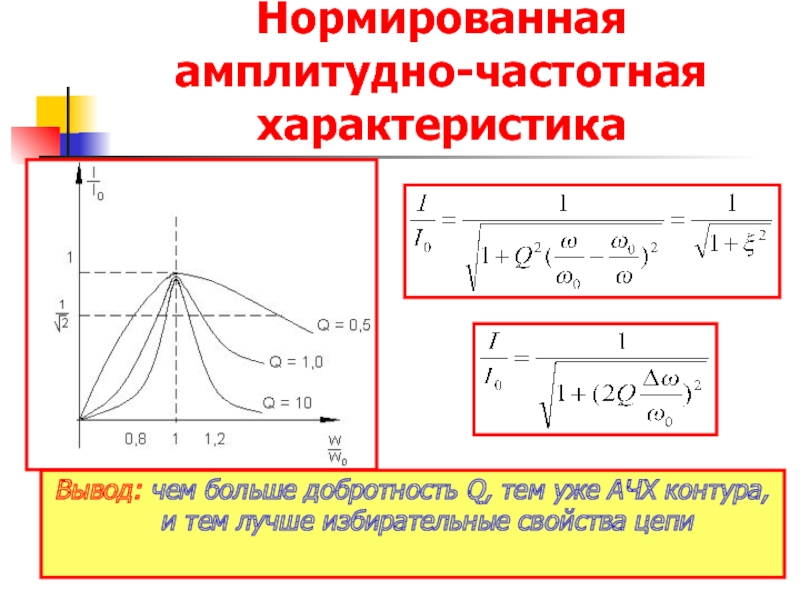
- 24. Нормированная амплитудно-частотная характеристика
- 25. Нормированная амплитудно-частотная характеристика Вывод:
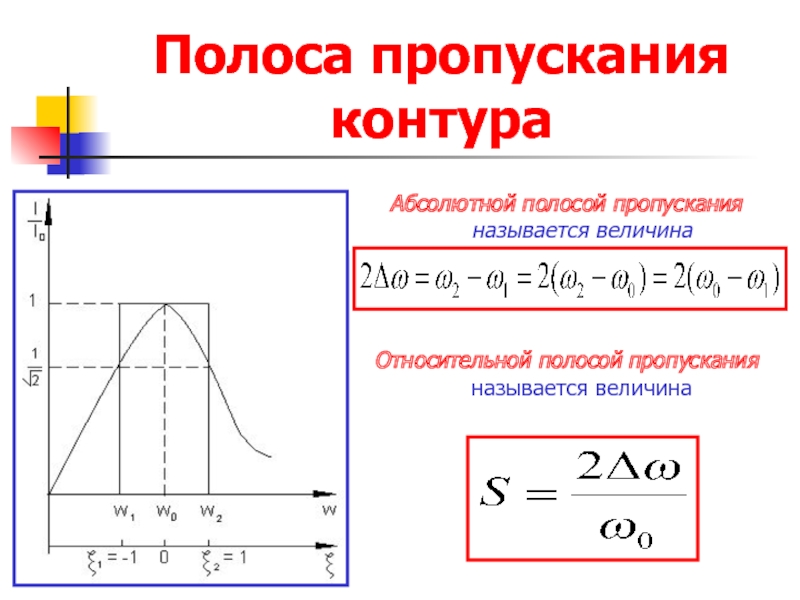
- 26. Полоса пропускания контура Абсолютной полосой пропускания называется
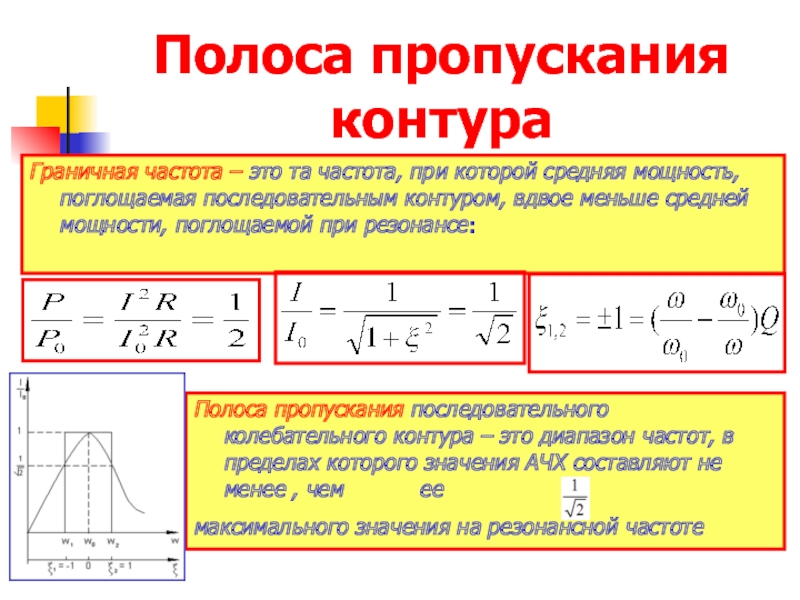
- 27. Полоса пропускания контура Граничная частота
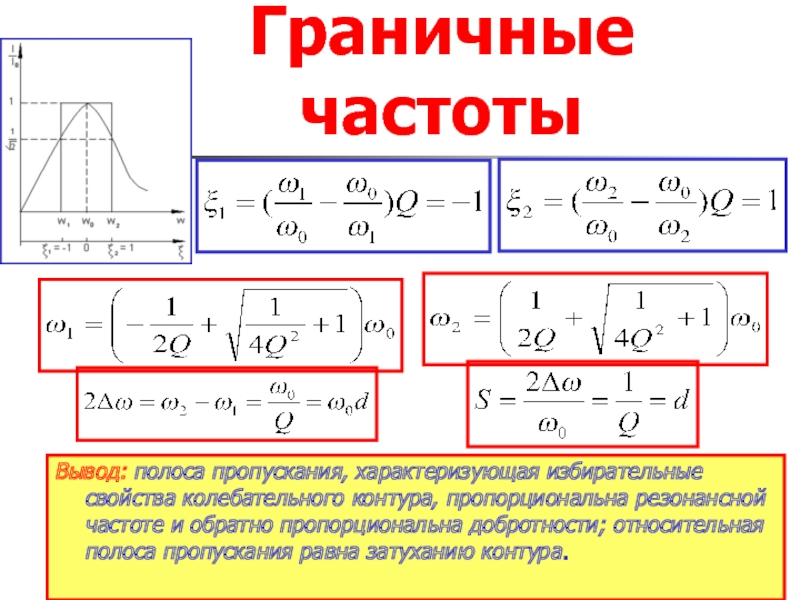
- 28. Граничные частоты
- 29. Параллельный колебательный контур Y1 =
- 30. РЕЗОНАНС В ПАРАЛЛЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ Основным
- 31. Резонансная частота и способы возбуждения резонанса токов
- 34. Свойства цепи при резонансе токов 3. Действующие
- 35. Свойства цепи при резонансе токов 4. Добротность
- 36. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПАРАЛЛЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА
- 37. Частотные характеристики Выводы 1. В дорезонансной области при ω
Слайд 3Учебные вопросы
1. Резонанс в последовательном колебательном контуре.
2. Частотные характеристики последовательного колебательного
3. Избирательные свойства последовательного колебательного контура.
4. Резонанс в параллельном колебательном контуре.
5. Частотные характеристики параллельного колебательного контура.
Слайд 4Литература
Попов В.П. Основы теории цепей: Учебник для вузов спец. "Радиотехника".-М.:
Слайд 5Режимы работы последовательной RLC-цепи
Векторные диаграммы напряжений и токов
Активно-индуктивный
Слайд 6Свойства активно-индуктивного режима последовательной RLC-цепи
- напряжение опережает ток источника;
- цепь
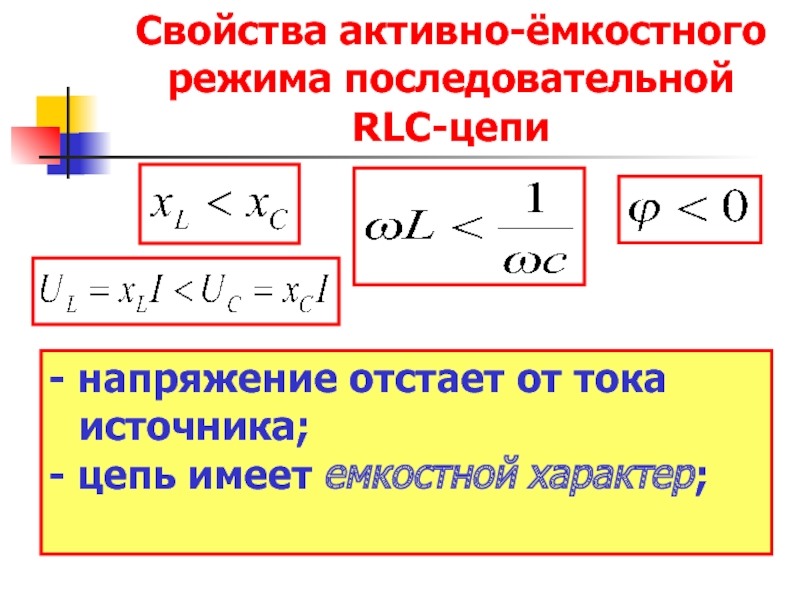
Слайд 7Свойства активно-ёмкостного режима последовательной RLC-цепи
- напряжение отстает от тока источника;
-
Слайд 8Свойства режима резонанса напряжений последовательной RLC-цепи
- напряжение на индуктивном и
- сопротивление цепи имеет чисто резистивный характер;
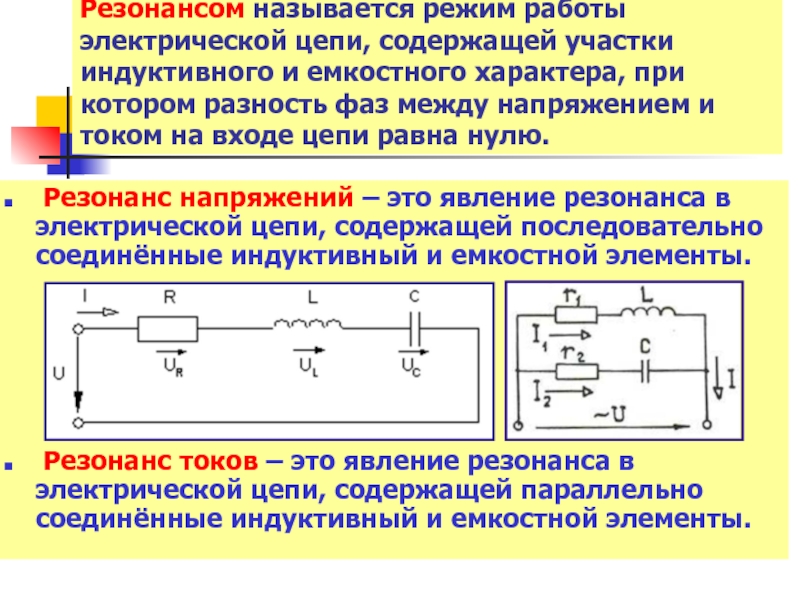
Слайд 9Резонансом называется режим работы электрической цепи, содержащей участки индуктивного и емкостного
Резонанс напряжений – это явление резонанса в электрической цепи, содержащей последовательно соединённые индуктивный и емкостной элементы.
Резонанс токов – это явление резонанса в электрической цепи, содержащей параллельно соединённые индуктивный и емкостной элементы.
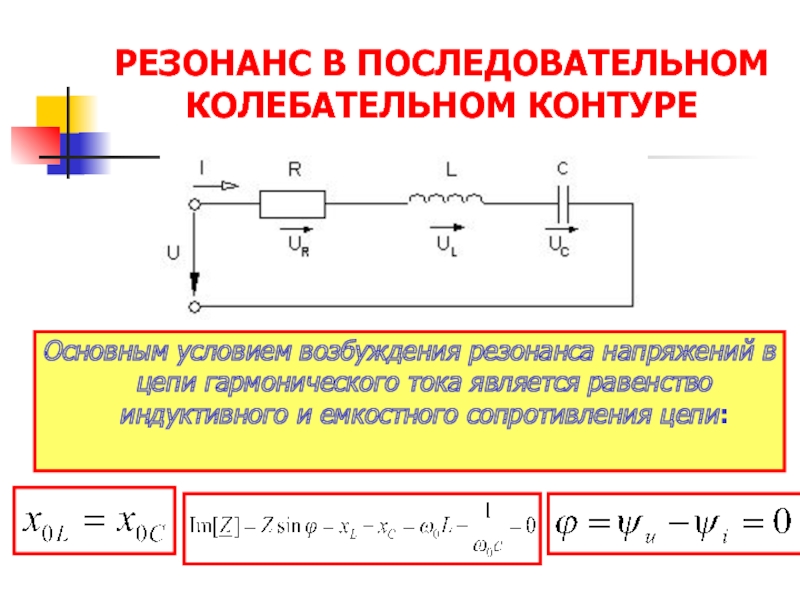
Слайд 10РЕЗОНАНС В ПОСЛЕДОВАТЕЛЬНОМ
КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Основным условием возбуждения резонанса напряжений в цепи
Слайд 11Характеристики резонанса напряжений
1. Резонансная частота:
2. Характеристическое (волновое) сопротивление:
3. Добротность и
Слайд 12Способы возбуждения резонанса
1 способ. При неизменных параметрах цепи
(L = const,
2 способ. При неизменной угловой частоте напряжения источника питания ( ω= const) необходимо изменять собственную угловую частоту цепи, изменяя ее параметры (L = var, C = var) и обеспечивая приближение собственной частоты контура к частоте напряжения источника питания:
Слайд 13
Свойства цепи при резонансе напряжений
1. Полное сопротивление цепи в резонансном
Слайд 14
Свойства цепи при резонансе напряжений
2. Ток в цепи при резонансе
Слайд 15
Свойства цепи при резонансе напряжений
3. Коэффициент мощности цепи равен единице,
Слайд 16
Свойства цепи при резонансе напряжений
4. В цепи имеют место обратимые
Все колебания энергии (обратимые ее преобразования) имеют место только в пределах внешней цепи, возврата энергии к источнику нет .
Слайд 17
Свойства цепи при резонансе напряжений
5. Энергия, потребляемая контуром от источника,
Слайд 18Физический смысл добротности контура
Добротность колебательного контура характеризует свойство колебательного контура запасать
Слайд 19
Свойства цепи при резонансе напряжений
6. Действующие значения напряжений на реактивных
Добротность контура показывает во сколько раз напряжения на реактивных элементах контура при резонансе превышает значение приложенного к контуру напряжения.
Слайд 20 ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА
Зависимости от частоты параметров контура:
Амплитудно-частотные характеристики
Фазо-частотная характеристика
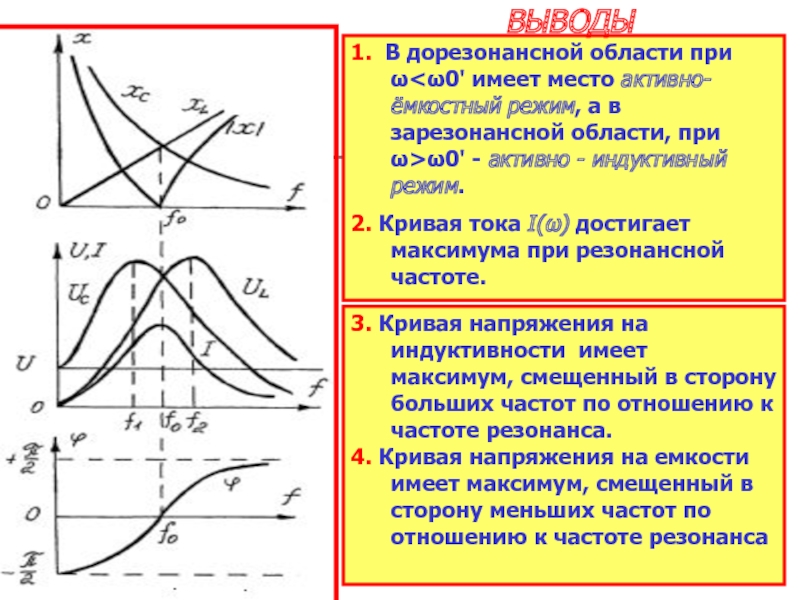
Слайд 221. В дорезонансной области при ω
2. Кривая тока I(ω) достигает максимума при резонансной частоте.
ВЫВОДЫ
3. Кривая напряжения на индуктивности имеет максимум, смещенный в сторону больших частот по отношению к частоте резонанса.
4. Кривая напряжения на емкости имеет максимум, смещенный в сторону меньших частот по отношению к частоте резонанса
Слайд 23Расстройки колебательных контуров
Абсолютная расстройка – разность между частотой колебаний, подводимых к
Относительная расстройка – отношение абсолютной расстройки к резонансной частоте.
Обобщенная расстройка –
Обобщенная расстройка для случая
малых расстроек -
Слайд 25Нормированная амплитудно-частотная характеристика
Вывод: чем больше добротность Q, тем уже АЧХ контура,
Слайд 26Полоса пропускания контура
Абсолютной полосой пропускания называется величина
Относительной полосой пропускания называется
Слайд 27Полоса пропускания контура
Граничная частота – это та частота, при которой средняя
Полоса пропускания последовательного колебательного контура – это диапазон частот, в пределах которого значения АЧХ составляют не менее , чем ее
максимального значения на резонансной частоте
Слайд 28Граничные частоты
Вывод: полоса пропускания, характеризующая избирательные свойства колебательного контура, пропорциональна резонансной
Слайд 29Параллельный колебательный контур
Y1 = =
-j = g1 + jb1,
Y2 = = = + = g2+ jb2
Параллельным колебательным контуром называется электрическая цепь, в которой индуктивность и емкость включены параллельно источнику сигнала.
Слайд 30РЕЗОНАНС В ПАРАЛЛЕЛЬНОМ
КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Основным условием возбуждения резонанса токов в цепи
Слайд 31Резонансная частота и способы возбуждения резонанса токов
ω0'=
Вывод: резонанса токов можно добиться теми же способами, которыми обеспечивается резонанс напряжений: изменением частоты приложенного к цепи напряжения ω или собственной резонансной частоты ω0', т.е. на основе равенства ω=ω0'.
Слайд 32
Свойства цепи при резонансе токов
1. Полная проводимость цепи при резонансе
Y=g+j (bС-bL)
Слайд 33
Свойства цепи при резонансе токов
2. Ток в цепи при резонансе
I0 = y0 ∙U = U∙ = U ∙g0 = U∙ymin= =Imin
Слайд 34Свойства цепи при резонансе токов
3. Действующие значения токов ветвей контура на
Слайд 35Свойства цепи при резонансе токов
4. Добротность параллельного колебательного контура совпадает с
Q = = = =
Слайд 36 ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПАРАЛЛЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА
Зависимости от частоты параметров
Амплитудно-частотные характеристики – это зависимости действующих или амплитудных значений тока от частоты:
Фазо-частотная характеристика
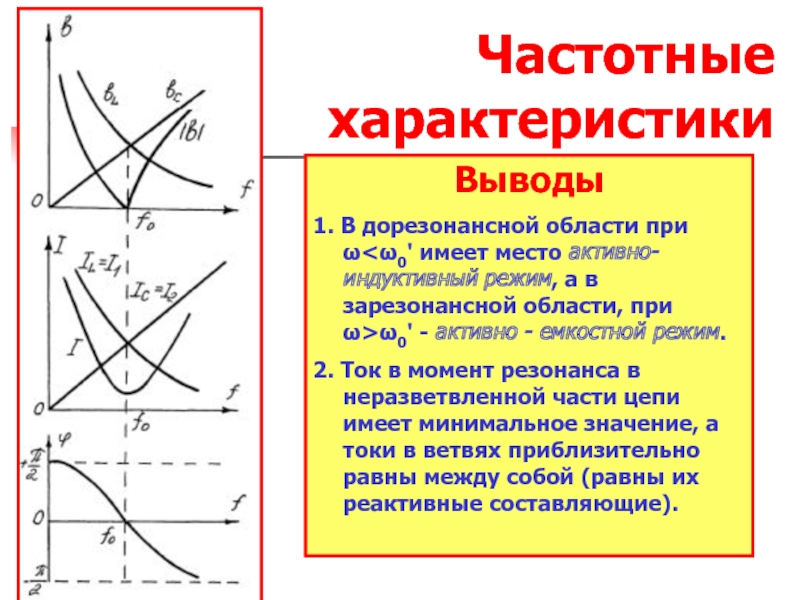
Слайд 37Частотные характеристики
Выводы
1. В дорезонансной области при ω
2. Ток в момент резонанса в неразветвленной части цепи имеет минимальное значение, а токи в ветвях приблизительно равны между собой (равны их реактивные составляющие).