- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретическая механика. Динамика. (Лекции 1-6) презентация
Содержание
- 1. Теоретическая механика. Динамика. (Лекции 1-6)
- 2. Рекомендуемая литература Часть 1: Теоретическая механика 1.
- 3. Содержание Лекция 1. Введение в динамику. Законы
- 4. Содержание Лекция 5. . Относительное движение материальной
- 5. ВВЕДЕНИЕ В ДИНАМИКУ Динамика –
- 6. Динамика механической системы – изучает движение совокупности
- 7. Отсюда вытекает: – существует абсолютно неподвижная система
- 8. Сила – величина переменная и зависит от:
- 9. 13. ОСНОВНЫЕ ВИДЫ СИЛ Сила тяжести.
- 10. В основе классической механики лежат законы, впервые
- 11. Закон пропорциональности силы и ускорения (Основное
- 12. Закон равенства действия и противодействия (III закон
- 17. Прямая задача: Задано движение (уравнения движения,
- 18. 2. Отбрасываем связь (трос) и
- 19. После подстановки найденных значений постоянных получаем:
- 20. 17. Общие указания к решению прямой и
- 21. 1.2. Изобразить точку в положении, соответствующем произвольному
- 22. 2. Решение дифференциальных уравнений:
- 23. 2.4. Вычислить неопределенные интегралы
- 24. 2.5. Выразить скорость через
- 25. Движение точки, брошенной под углом к
- 26. x 19. Виды колебаний материальной точки 1.
- 27. x Данное уравнение является однородным линейным дифференциальным
- 28. Затухающие колебания материальной точки – колебательное движение
- 29. 20. Относительное движение материальной точки
- 30. Спасибо за внимание!
- 31. Лекция 2 Система материальных точек или механическая
- 32. Лекция 2 В дополнение к ранее существовавшей
- 34. Для описания движения системы в целом вводится
- 35. Рассмотрим систему n материальных точек. Приложенные к
- 36. Следствия из теоремы о движении центра масс
- 37. Мера механического взаимодействия, характеризующая передачу механического движения
- 38. Мера механического движения, определяемая вектором, равным произведению
- 39. Рассмотрим систему n материальных точек. Приложенные
- 40. : 1. Если в интервале времени [t1,
- 41. Мера механического движения, определяемая вектором, равным векторному
- 42. Рассмотрим систему n материальных точек. Приложенные
- 43. Заменим сумму производных на производную суммы:
- 44. Теорема: Производная вектора момента количества движения системы
- 45. Если в интервале времени [t1, t2] вектор
- 46. Момент инерции материальной точки относительно оси равен
- 47. 30.2. Момент инерции твердого тела относительно оси
- 48. 30.4. Момент инерции однородного стержня постоянного сечения
- 49. 30.5. Момент инерции однородного сплошного цилиндра относительно
- 50. 31. Кинетический момент твердого тела
- 51. 32. Дифференциальное уравнение вращения твердого тело
- 52. Гироскоп – твердое тело, вращающееся вокруг оси
- 53. Основное допущение приближенной (элементарной) теории гироскопа –
- 54. В случае действия силы, приложенной к оси
- 55. При прекращении действия силы ось ротора останется
- 56. Спасибо за внимание!
- 57. 17 Пример: Два человека массами
- 58. Лекция 6 (продолжение 6.2)
- 59. Лекция 8 (продолжение 8.2)
- 60. Теорем: Применение теоремы об изменении количества движения
Слайд 1Санкт-Петербург
- 2016 -
Санкт-Петербургский государственный университет
гражданской авиации
Кафедра № 6 - «Механики»
Раздел
«ДИНАМИКА»
Слайд 2Рекомендуемая литература
Часть 1: Теоретическая механика
1. Яблонский А.А., Никифорова В.М. Курс теоретической
2. Мещерский И.В. Задачи по теоретической механике. Учеб. Пособие. СПб.: Лань. 2011. - 448 с.
3. Тарг М.С. Курс теоретической механики. М.: Высшая школа. 2012. - 548 с.
4. Чернов К.И. Основы технической механики. М.: Машиностроение. 1986. - 256 с.
5. Арет В.А. «Дистанционное обучающихся технология». (электронное пособие www.5. Арет В.А. «Дистанционное обучающихся технология». (электронное пособие www.open-mechanics.com), 2016 г.
Слайд 3Содержание
Лекция 1. Введение в динамику. Законы и аксиомы динамики материальной точки.
Лекция 2. Решение обратной задачи динамики. Общие указания к решению обратной задачи динамики. Примеры решения обратной задачи динамики. Движение тела, брошенного под углом к горизонту, без учета сопротивления воздуха.
Лекция 3. Прямолинейные колебания материальной точки. Условие возникновения колебаний. Классификация колебаний. Свободные колебания без учета сил сопротивления. Затухающие колебания. Декремент колебаний.
Лекция Лекция 4. Вынужденные колебания материальной точки. Резонанс. Влияние сопротивления движению при вынужденных колебаниях.
Слайд 4Содержание
Лекция 5. . Относительное движение материальной точки. Силы инерции. Частные случаи
Лекция 6. Динамика механической системы. Механическая система. Внешние и внутренние силы. Центр масс системы. Теорема о движении центра масс. Законы сохранения. Пример решения задачи на использование теоремы о движении центра масс.
Лекция 7. Импульс силы. Количество движения. Теорема об изменении количества движения. Законы сохранения. Теорема Эйлера. Пример решения задачи на использование теоремы об изменении количества движения. Момент количества движения. Теорема об изменении момента количества движения..
Лекция 8. Законы сохранения. Элементы теории моментов инерции. Кинетический момент твердого тела. Дифференциальное уравнение вращения твердого тела. Пример решения задачи на использование теоремы об изменении момента количества движения системы. Элементарная теория гироскопа.
Слайд 5
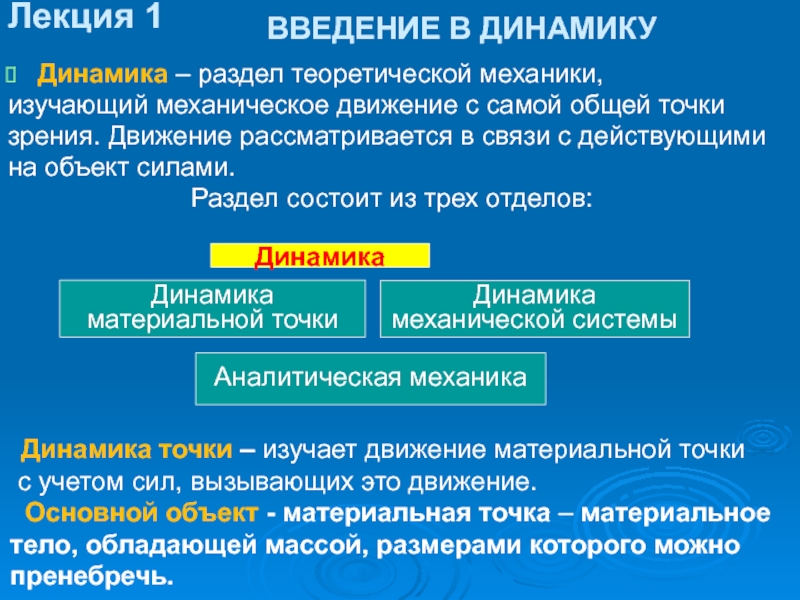
ВВЕДЕНИЕ В ДИНАМИКУ
Динамика – раздел теоретической механики,
изучающий механическое движение с самой
зрения. Движение рассматривается в связи с действующими
на объект силами.
Раздел состоит из трех отделов:
Лекция 1
Динамика
материальной точки
Динамика
Динамика
механической системы
Аналитическая механика
Динамика точки – изучает движение материальной точки
с учетом сил, вызывающих это движение.
Основной объект - материальная точка – материальное тело, обладающей массой, размерами которого можно пренебречь.
Слайд 6Динамика механической системы – изучает движение совокупности материальных точек и твердых
Аналитическая механика – изучает движение несвободных механических систем с использованием общих аналитических методов.
Основные допущения:
– существует абсолютное пространство (обладает чисто геометрическими свойствами, не зависящими от материи и ее движения);
– существует абсолютное время (не зависит от материи и ее движения).
Слайд 7Отсюда вытекает:
– существует абсолютно неподвижная система отсчета;
– время не зависит от
– массы движущихся точек не зависят от движения системы отсчета.
Эти допущения используются в классической механике, созданной Галилеем и Ньютоном. Она имеет до сих пор достаточно широкую область применения, поскольку рассматриваемые в прикладных науках механические системы не обладают такими большими массами и скоростями движения, для которых необходим учет их влияния на геометрию пространства, время, движение, как это делается в релятивистской механике (теории относительности).
Слайд 8Сила – величина переменная и зависит от:
а) времени -
б) положения
в) скорости перемещения
точки приложения силы -
Материальная точка может быть свободной, если на ее перемещение не наложены ограничения. В противном случае, материальная точка называется несвободной
Инертность - это свойство материального тела быстрее или медленнее изменять скорость своего движения под действием приложенных к нему сил
Инерциальными системами отсчета являются такие системы, где выполняется закон инерции; в противном случае, системы отсчета являются неинерциальными
Слайд 913. ОСНОВНЫЕ ВИДЫ СИЛ
Сила тяжести.
м./c2
Сила трения скольжения
коэффициент трения
нормальная реакция.
ускорение
Сила тяготения.
гравитационная постоянная
м3/(кг с2).
Сила упругости
удлинение (сжатие) пружины (м)
Сила вязкого трения.
коэффициент жесткости пружины (Н/м).
скорость тела
коэффициент сопротивления
медленное движение
Сила гидродинамического
сопротивления.
быстрое движение
плотность среды
коэффициент сопротивления
площадь поперечного сечения
Слайд 10В основе классической механики лежат законы, впервые изложенные И. Ньютоном в
Основные законы динамики – впервые открытые Галилеем и сформулированные Ньютоном составляют основу всех методов описания и анализа движения механических систем и их динамического взаимодействия под действием различных сил.
Закон инерции (закон Галилея-Ньютона) – Изолированная материальная точка тело сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, приложенные силы не заставят ее изменить это состояние.
Отсюда следует эквивалентность состояния покоя и движения по инерции (закон относительности Галилея). Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной. Свойство материальной точки стремиться сохранить неизменной скорость своего движения (свое кинематическое состояние) называется инертностью.
14. Законы и аксиомы динамики мат-ной точки
Слайд 11 Закон пропорциональности силы и ускорения (Основное уравнение динамики - II
Здесь m – масса точки (мера инертности), измеряется в кг,
численно равна весу, деленному на ускорение свободного падения:
F – действующая сила, измеряется в Н (1 Н сообщает точке массой 1 кг ускорение 1 м/c2, 1 Н = 1/9.81 кгс).
Слайд 12Закон равенства действия и противодействия (III закон Ньютона) - Всякому действию
Закон справедлив для любого кинематического состояния тел. Силы взаимодействия, будучи приложенные к разным точкам (телам) не уравновешиваются.
Закон независимости действия сил – Ускорение материальной точки под действием нескольких сил равно геометрической сумме ускорений точки от действия каждой из сил в отдельности:
или
Слайд 13
Основное уравнение динамики :
- соответствует векторному способу задания движения точки.
15.
Основной закон динамики: произведение массы материальной точки на ее ускорение, которое она получает под действием силы, равно модулю этой силы, и направление ускорения совпадает с направлением вектора силы
или
Слайд 14
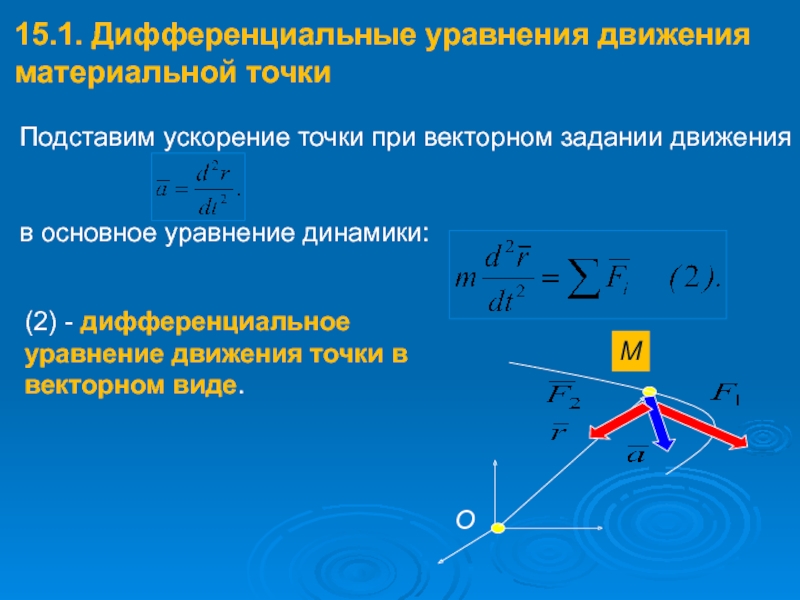
15.1. Дифференциальные уравнения движения материальной точки
Подставим ускорение точки при векторном задании
в основное уравнение динамики:
(2) - дифференциальное уравнение движения точки в векторном виде.
Слайд 15
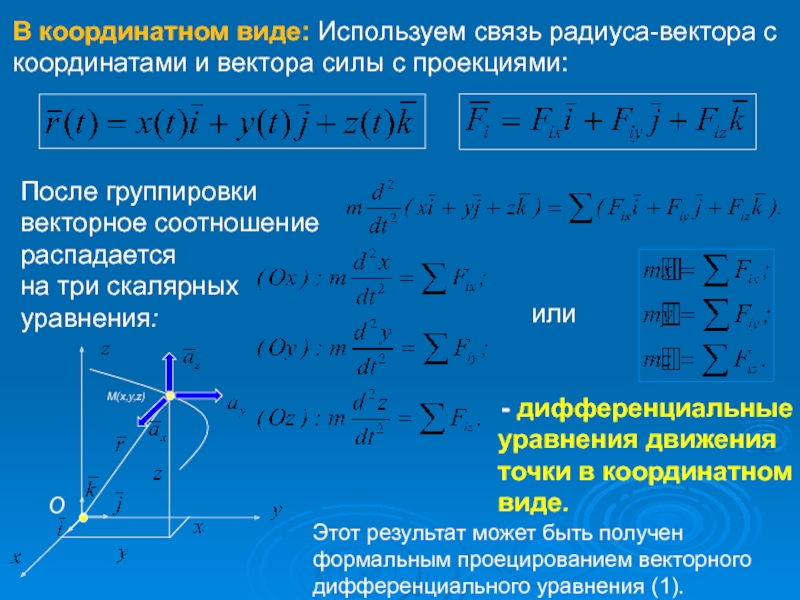
- дифференциальные
уравнения движения
точки в координатном
виде.
Этот результат может быть получен формальным
После группировки
векторное соотношение
распадается
на три скалярных
уравнения:
В координатном виде: Используем связь радиуса-вектора с координатами и вектора силы с проекциями:
или
Слайд 16
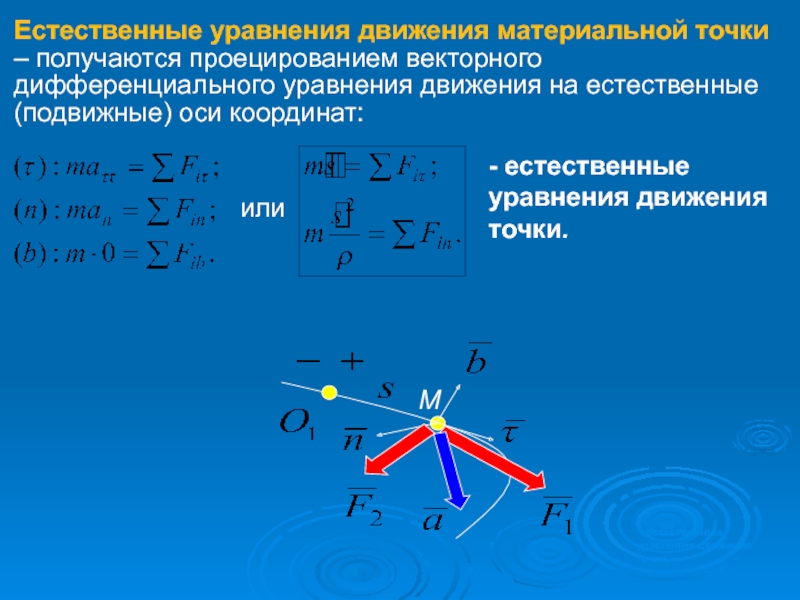
Естественные уравнения движения материальной точки – получаются проецированием векторного дифференциального уравнения
- естественные
уравнения движения
точки.
или
- естественные
уравнения движения
точки.
Слайд 17 Прямая задача: Задано движение (уравнения движения, траектория). Требуется определить силы,
Обратная задача: Заданы силы, под действием которых происходит движение. Требуется найти параметры движения (уравнения движения, траекторию движения).
Обе задачи решаются с помощью основного уравнения динамики и проекции его на координатные оси. Если рассматривается движение несвободной точки, то как и в статике, используется принцип освобождаемости от связей. В результате реакции связей включаются в состав сил, действующих на материальную точку. Решение первой задачи связано с операциями дифференцирования. Решение обратной задачи требует интегрирования соответствующих дифференциальных уравнений и это значительно сложнее, чем дифференцирование. Обратная задача сложнее прямой задачи
y
O
r
16. Две основные задачи динамики
Слайд 18
2. Отбрасываем связь (трос) и заменяем реакцией R.
3. Составляем основное уравнение
Определяем реакцию троса:
Определяем натяжение троса:
При равномерном движении кабины ay = 0 и натяжение троса равно весу: T = G.
При обрыве троса T = 0 и ускорение кабины равно ускорению свободного падения: ay = -g.
4. Проецируем основное уравнение динамики на ось y:
y
O
Решение прямой задачи динамики - рассмотрим на примерах:
Пример 1. Кабина лифта весом G поднимается тросом с ускорением a . Определить натяжение троса.
Решение: 1. Выбираем объект (кабина лифта движется поступательно и ее можно рассматривать как материальную точку).
Слайд 19После подстановки найденных
значений постоянных получаем:
Таким образом, под действием одной и
материальная точка может совершать целый класс движений,
определяемых начальными условиями.
Начальные координаты учитывают исходное положение точки. Начальная скорость, задаваемая проекциями, учитывает влияние на ее движение по рассматриваемому участку траектории сил, действовавших на точку до прихода на этот участок, т.е. начальное кинематическое состояние.
Решение обратной задачи динамики – В общем случае движения точки силы, действующие на точку, являются переменными, зависящими от времени, координат и скорости. Движение точки описывается системой трех дифференциальных уравнений второго порядка:
После интегрирования
каждого из них будет
шесть постоянных
C1, C2,…., C6:
Значения постоянных C1, C2,…., C6
находятся из шести начальных
условий при t = 0:
x
Слайд 2017. Общие указания к решению прямой и обратной задачи. Порядок решения
1.
1.1. Выбрать систему координат – прямоугольную (неподвижную) при неизвестной траектории движения, естественную (подвижную) при известной траектории, например, окружность или прямая линия. В последнем случае можно использовать одну прямолинейную координату. Начало отсчета совместить с начальным положением точки (при t = 0) или с равновесным положением точки, если оно существует, например, при колебаниях точки.
Слайд 211.2. Изобразить точку в положении, соответствующем произвольному моменту времени (при t
1.3. Освободить материальную точку от связей, заменить их действие реакциями, добавить активные силы.
1.4. Записать основной закон динамики в векторном виде, спроецировать на выбранные оси, выразить задаваемые или реактивные силы через переменные время, координаты или скорости, если они от них зависят.
Слайд 22
2. Решение дифференциальных уравнений:
2.1. Понизить производную, если уравнение не приводится к
2.2. Разделить переменные, например:
2.3. Если в уравнении три переменных,
то сделать замену переменных, например:
и затем разделить переменные.
или
Слайд 23
2.4. Вычислить неопределенные интегралы в левой и правой частях уравнения, например:
Замечание.
Нижние пределы представляют начальные значения переменных (начальные условия) .Тогда не требуется отдельного нахождения постоянной, которая автоматически включается в решение, например:
Используя начальные условия, например, t = 0, vx = vx0, определить постоянную интегрирования:
Слайд 24
2.5. Выразить скорость через производную координаты по времени, например,
Замечание. Если уравнение приводится к каноническому виду, имеющему стандартное решение, то это готовое решение и используется.
Постоянные интегрирования по прежнему находятся из начальных условий.
Слайд 25 Движение точки, брошенной под углом к горизонту, в однородном поле
18. Динамика свободной материальной точки
Слайд 26x
19. Виды колебаний материальной точки
1. Свободные колебания (без учета сопротивления среды).
2.
3. Вынужденные колебания.
4. Вынужденные колебания с учетом сопротивления среды.
Свободные колебания – происходят под действием только восстанавливающей силы.
Запишем основной закон динамики:
Выберем систему координат с центром в положении равновесия (точке O) и спроецируем
уравнение на ось x :
Приведём полученное уравнение
к стандартному (каноническому) виду :
x
y
O
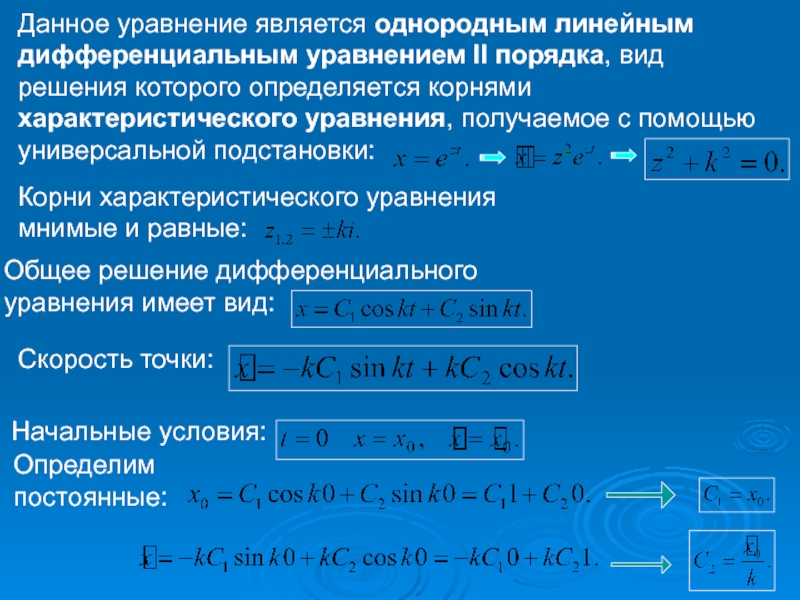
Слайд 27x
Данное уравнение является однородным линейным дифференциальным уравнением II порядка, вид решения
Корни характеристического уравнения
мнимые и равные:
Общее решение дифференциального
уравнения имеет вид:
Скорость точки:
Начальные условия:
Определим
постоянные:
Слайд 28Затухающие колебания материальной точки – колебательное движение материальной точки происходит при
Зависимость силы сопротивления движению от смещения или скорости определяется физической природы среды или связи, препятствующей движению. Наиболее простой зависимостью является линейная зависимость от скорости (вязкое сопротивление).
Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени.
Слайд 2920. Относительное движение материальной точки
Основное уравнение динамики:
Абсолютное ускорение точки:
Перенесем слагаемые
Перенесенные слагаемые имеют размерность сил и рассматриваются как соответствующие силы
инерции, равные:
Тогда относительное движение точки можно рассматривать как абсолютное, если к действующим силам добавить переносную и кориолисову силы инерции:
В проекциях на оси подвижной системы
координат имеем:
Положим, что подвижная (неинерциальная) система координат Oxyz движется по некоторому закону относительно неподвижной (инерциальной) системы координат O1x1y1z1. Движение материальной точки M (x, y, z) относительно подвижной системы Oxyz– относительное, относительно неподвижной системы O1x1y1z1– абсолютное. Движение подвижной системы Oxyz относительно неподвижной системы O1x1y1z1– переносное движение.
Слайд 31Лекция 2
Система материальных точек или механическая система – Совокупность материальных точек
Система свободных точек - движение которых не ограничивается никакими связями (например, планетная система, в которой планеты рассматриваются как материальные точки).
Система несвободных точек или несвободная механическая система – движение материальных точек или тел ограничиваются наложенными на систему связями (например, механизм, машина и т.п.).
21. Динамика механической системы
Слайд 32Лекция 2
В дополнение к ранее существовавшей классификации сил (активные и реактивные
классификация сил:
1. Внешние силы (e) – действующие на точки и тела системы со стороны точек или тел, не входящих в состав данной системы.
2. Внутренние силы (i) – силы взаимодействия между материальными точками или телами, входящими в данную систему.
Одна и та же сила может являться как внешней, так и внутренней силой. Все зависит от того, какая механическая система рассматривается.
Например: В системе Солнце, Земля и Луна все силы тяготения между ними являются внутренними. При рассмотрении системы Земля и Луна силы тяготения, приложенные со стороны Солнца – внешние.
22. Силы, действующие на систему
Слайд 33
А
З
В
На основании закона действия и противодействия каждой внутренней силе
сила , равная по модулю и противоположная по направлению.
Из этого следуют два замечательных свойства внутренних сил:
Главный вектор всех внутренних сил системы равен нулю:
2. Главный момент всех внутренних сил системы относительно любого центра равен нулю:
Или в проекциях на координатные оси:
Замечание: Хотя эти уравнения похожи на уравнения равновесия, они таковыми не являются, поскольку внутренние силы приложены к различным точкам или телам системы и могут вызывать движение этих точек (тел) относительно друг друга. Из этих уравнений следует,
что внутренние силы не влияют на движение системы, рассматриваемой как одно целое.
С
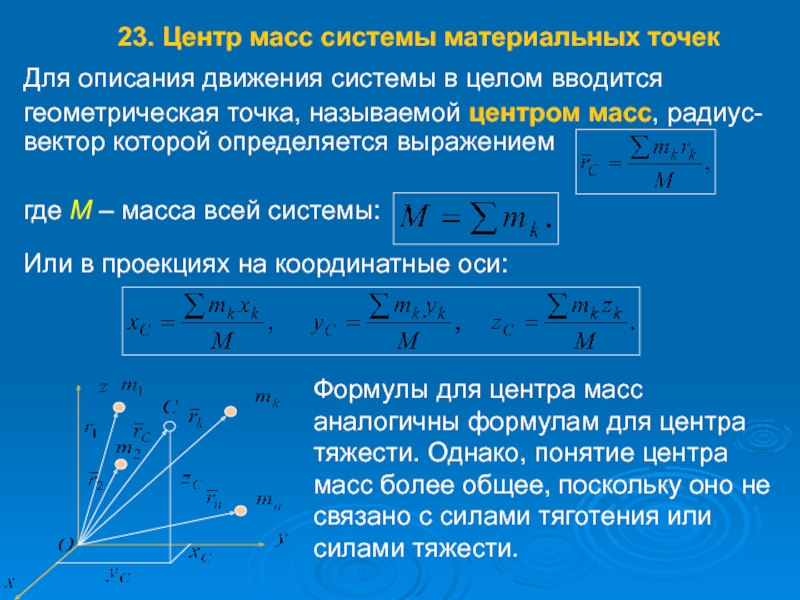
Слайд 34Для описания движения системы в целом вводится
геометрическая точка, называемой центром
где M – масса всей системы:
Или в проекциях на координатные оси:
Формулы для центра масс аналогичны формулам для центра тяжести. Однако, понятие центра масс более общее, поскольку оно не связано с силами тяготения или силами тяжести.
23. Центр масс системы материальных точек
Слайд 35Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим
Просуммируем эти уравнения
по всем точкам:
В проекциях на координатные оси:
24. Теорема о движении центра масс системы
или
Теорем: Произведение массы системы на ускорение ее центра массе равно главному вектору внешних сил.
Слайд 36Следствия из теоремы о движении центра масс системы
(законы сохранения)
1. Если в
2. Если в интервале времени [t1, t2] проекция главного вектора внешних сил системы на ось x равна нулю, Rxe = 0, то скорость центра масс по оси x постоянна, vCx = const (центр масс движется по оси равномерно).
3. Если в интервале времени [t1, t2] главный вектор внешних сил системы
равен нулю, Re = 0, и в начальный момент скорость центра масс равна нулю, vC = 0, то радиус-вектор центра масс остается постоянным, rC = const (центр масс находится в покое – закон сохранения положения центра масс).
4. Если в интервале времени [t1, t2] проекция главного вектора внешних сил системы на ось x равна нулю, Rxe = 0, и в начальный момент скорость центра масс по этой оси равна нулю, vCx = 0, то координата центра масс по оси x остается постоянной, xC = const (центр масс не движется по этой оси).
Аналогичные утверждения справедливы для осей y и z.
Слайд 37Мера механического взаимодействия, характеризующая передачу механического движения со стороны действующих на
В случае постоянной силы:
В проекциях на
координатные
оси:
Импульс равнодействующей – равен геометрической сумме импульсов приложенных к точке сил за один и тот же промежуток времени:
Проинтегрируем на
данном промежутке
времени:
25. Импульс силы
Слайд 38Мера механического движения, определяемая вектором, равным произведению массы точки на вектор
Количество движения системы материальных точек – геометрическая сумма количеств движения материальных точек:
По определению центра масс:
Тогда:
В проекциях на координатные оси:
26. Количество движения точки
Вектор количества движения системы равен произведению массы всей системы на вектор скорости центра масс системы.
Слайд 39 Рассмотрим систему n материальных точек. Приложенные к каждой точке силы
Производная вектора количества движения системы по времени равна главному вектору внешних сил системы.
Просуммируем эти уравнения
по всем точкам:
В левой части уравнения внесем массы под знак производной
и заменим сумму производных на производную суммы:
Из определения
количества
движения системы:
В проекциях на координатные
оси:
26. Теорема об изменении количества движения системы
или
Слайд 40:
1. Если в интервале времени [t1, t2] главный вектор внешних сил
2. Если в интервале времени [t1, t2] проекция главного вектора внешних сил системы на ось x равна нулю, Rxe = 0, то проекция количества движения системы на ось x постоянна, Qx = const.
Аналогичные утверждения справедливы для осей y и z.
Проецируем на ось τ :
τ
Разделяем
переменные
и интегрируем :
Правый интеграл практически равен нулю, т.к. время взрыва t<<1.
Отсюда закон сохранения :
26. Следствия из теоремы об изменении количества движения системы (законы сохранения)
Слайд 41Мера механического движения, определяемая вектором, равным векторному произведению радиуса-вектора материальной точки
Кинетический момент системы материальных точек относительно некоторого центра – геометрическая сумма моментов количеств движений всех материальных точек относительно этого же центра:
В проекциях на оси:
Производная вектора момента количества движения системы относительно некоторого центра по времени равна главному моменту внешних сил системы относительно этого же центра.
27. Момент количества движения точки или кинетический момент движения относительно некоторого центра
Слайд 42
Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим
или
Просуммируем эти уравнения по всем
точкам:
Умножим векторно каждое из равенств на радиус-вектор слева:
28. Теорема об изменении момента количества движения системы
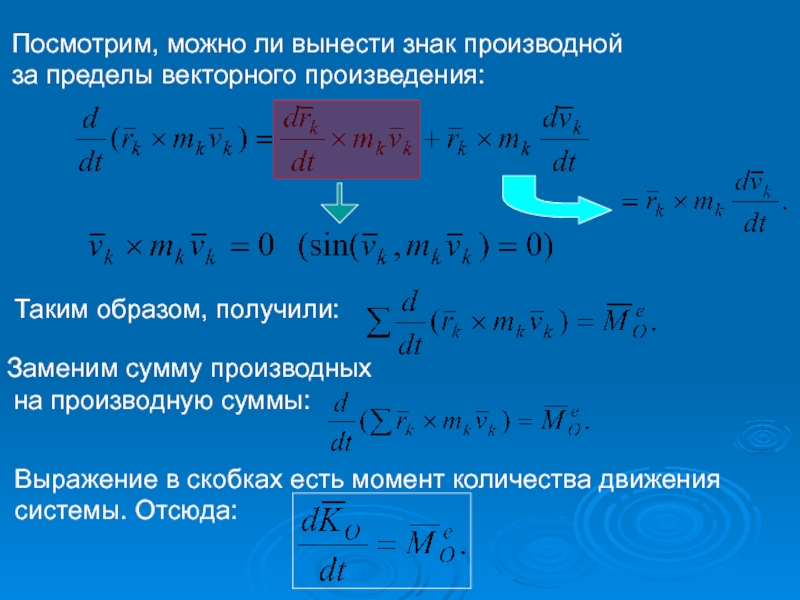
Слайд 43Заменим сумму производных
на производную суммы:
Выражение в скобках есть момент количества
Посмотрим, можно ли вынести знак производной
за пределы векторного произведения:
Таким образом, получили:
Слайд 44Теорема: Производная вектора момента количества движения системы относительно некоторого центра по
В проекциях на координатные оси:
Теорема: Производная момента количества движения системы относительно некоторой оси по времени равна главному моменту внешних сил системы относительно этой же оси.
Слайд 45Если в интервале времени [t1, t2] вектор главного момента внешних сил
2. Если в интервале времени [t1, t2] главный момент внешних сил системы относительно оси x равен нулю, Mxe = 0, то момент количества движения системы относительно оси x постоянен, Kx = const.
Аналогичные утверждения справедливы для осей y и z.
29. Следствия из теоремы об изменении момента количества движения системы (законы сохранения)
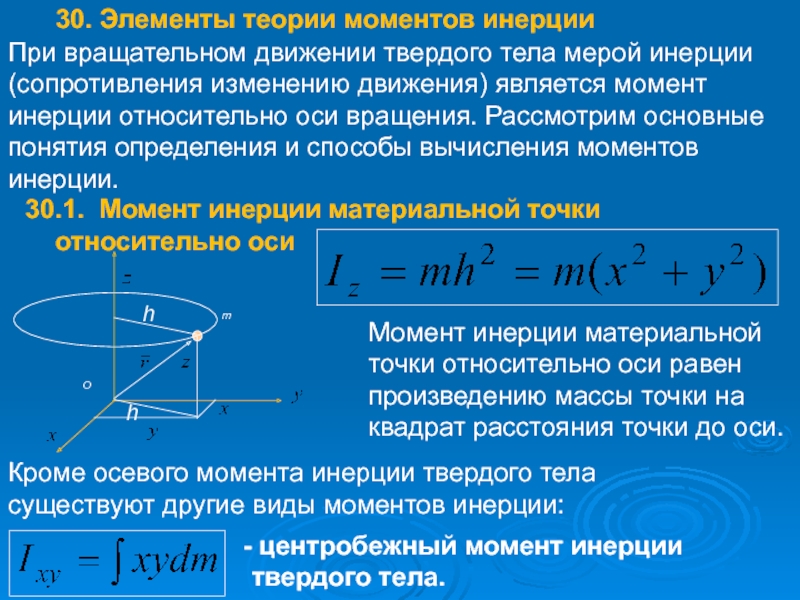
Слайд 46Момент инерции материальной
точки относительно оси равен
произведению массы точки на
квадрат расстояния точки
30.1. Момент инерции материальной точки относительно оси
Кроме осевого момента инерции твердого тела
существуют другие виды моментов инерции:
центробежный момент инерции твердого тела.
30. Элементы теории моментов инерции
При вращательном движении твердого тела мерой инерции (сопротивления изменению движения) является момент инерции относительно оси вращения. Рассмотрим основные понятия определения и способы вычисления моментов инерции.
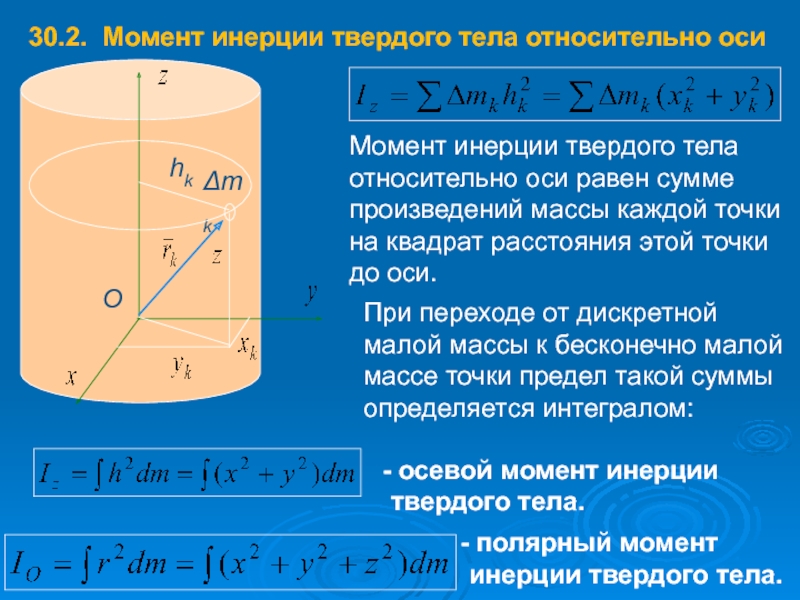
Слайд 4730.2. Момент инерции твердого тела относительно оси
Момент инерции твердого тела относительно
При переходе от дискретной малой массы к бесконечно малой массе точки предел такой суммы определяется интегралом:
осевой момент инерции
твердого тела.
полярный момент инерции твердого тела.
Слайд 4830.4. Момент инерции однородного стержня постоянного сечения относительно оси
x
z
L
Выделим элементарный объем
x
dx
Элементарная
масса:
Для вычисления момента инерции относительно центральной
оси (проходящей через центр тяжести) достаточно изменить
расположение оси и задать пределы интегрирования (-L/2, L/2). Здесь продемонстрируем формулу перехода к параллельным осям:
zС
C
Слайд 4930.5. Момент инерции однородного сплошного цилиндра относительно оси симметрии
Выделим элементарный объем:
Элементарная масса:
Поскольку высота цилиндров в результате не входит в формулы моментов инерции, то они остаются справедливыми для тонкого сплошного диска и обода колеса (тонкого кольца).
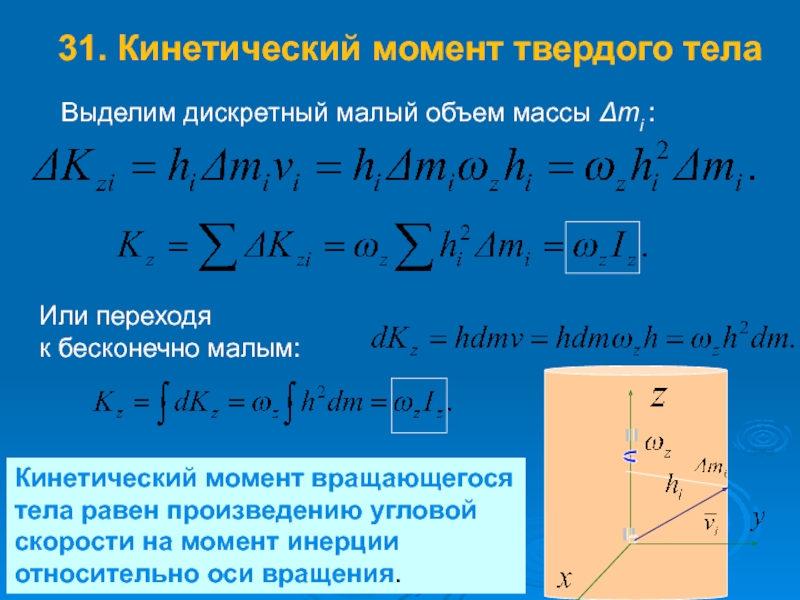
Слайд 50 31. Кинетический момент твердого тела
Выделим дискретный малый объем массы Δmi
Или переходя
к бесконечно малым:
Кинетический момент вращающегося тела равен произведению угловой скорости на момент инерции относительно оси вращения.
Слайд 51
32. Дифференциальное уравнение вращения твердого тело относительно оси
Запишем теорему об изменении
твердого тела, вращающегося вокруг неподвижной оси:
Кинетический момент вращающегося твердого тела равен:
Момент внешних сил относительно оси вращения равен вращающему моменту (реакции и сила тяжести
моментов не создают):
Подставляем кинетический момент и
вращающий момент в теорему
Слайд 52Гироскоп – твердое тело, вращающееся вокруг оси материальной симметрии, одна из
Свободный гироскоп – закреплен так, что его центр масс остается неподвижным, а ось вращения проходит через центр масс и может принимать любое положение в пространстве, т.е. ось вращения изменяет своё положение подобно оси собственного вращения тела при сферическом движении.
ω
33. Элементарная теория гироскопа
Слайд 53Основное допущение приближенной (элементарной) теории гироскопа – вектор момента количества
движения (кинетический
Основное свойство свободного гироскопа – ось ротора сохраняет неизменное направление в пространстве по отношению к инерциальной (звездной) системе отсчета (демонстрируется маятником Фуко, сохраняющим неизменной по отношению к звездам плоскость качания, 1852 г.).
Это вытекает из закона сохранения кинетического момента относительно центра масс ротора при условии пренебрежения трением в подшипниках осей подвески ротора, внешней и внутренней рамы:
Слайд 54В случае действия силы, приложенной к оси ротора,
момент внешних сил относительно
ω
С
Производная кинетического момента по времени
равна скорости конца этого вектора (теорема Резаля):
Это означает, что ось ротора будет отклоняться не в сторону действия силы, а в сторону вектора момента
этой силы, т.е. будет поворачиваться не относительно оси x (внутренняя подвеска), а относительно оси y
(внешняя подвеска).
34. Действие силы на ось свободного гироскопа
Слайд 55При прекращении действия силы ось ротора останется
в неизменном положении, соответствующем
последнему
с этого момента времени момент внешних сил вновь
становится равным нулю.
В случае кратковременного действия силы (удара) ось гироскопа практически не меняет своего положения.
Таким образом, быстрое вращение ротора сообщает гироскопу способность противодействовать случайным воздействиям, стремящимся изменить положение оси вращения ротора, а при постоянном действии силы сохраняет положение плоскости, перпендикулярной действующей силе, в которой лежит ось ротора. Эти свойства используются в работе инерциальных систем навигации.
Слайд 57
17
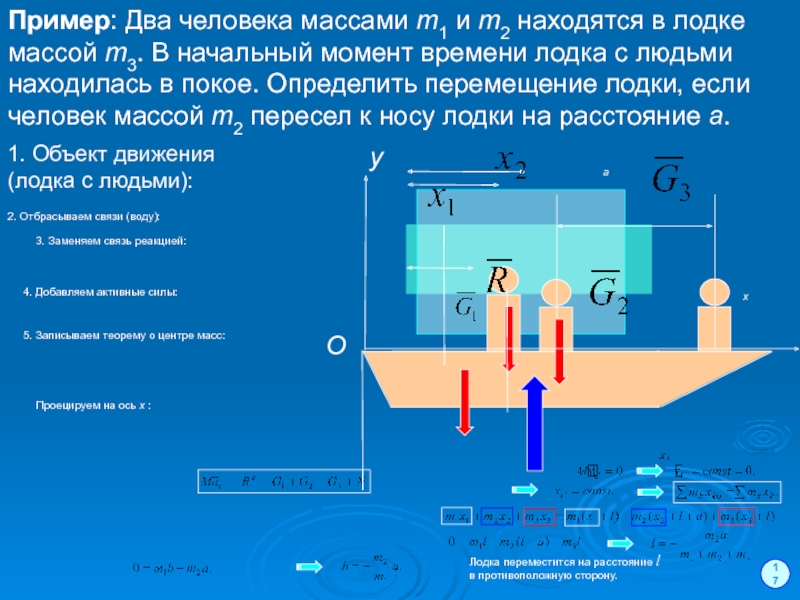
Пример: Два человека массами m1 и m2 находятся в лодке массой
1. Объект движения (лодка с людьми):
2. Отбрасываем связи (воду):
3. Заменяем связь реакцией:
4. Добавляем активные силы:
5. Записываем теорему о центре масс:
Проецируем на ось x :
O
Лодка переместится на расстояние l в противоположную сторону.
Слайд 58
Лекция 6 (продолжение 6.2)
17
Теорема о движении центра масс системы – Рассмотрим
Просуммируем эти уравнения
по всем точкам:
В левой части уравнения внесем массы под знак производной
и заменим сумму производных на производную суммы:
Из определения центра масс:
Подставим в полученное уравнение:
После вынесения массы системы
за знак производной получаем или:
Произведение массы системы на ускорение ее центра массе равно главному вектору внешних сил.
В проекциях на координатные оси:
Центр масс системы движется как материальная точка массой, равной массе
всей системы, к которой приложены все внешние силы, действующие на систему.
Следствия из теоремы о движении центра масс системы
(законы сохранения):
1. Если в интервале времени [t1, t2] главный вектор внешних сил системы
равен нулю, Re = 0, то скорость центра масс постоянна, vC = const
(центр масс движется равномерно прямолинейно – закон сохранения
движения центра масс).
2. Если в интервале времени [t1, t2] проекция главного вектора внешних сил
системы на ось x равна нулю, Rxe = 0, то скорость центра масс по оси x
постоянна, vCx = const (центр масс движется по оси равномерно).
Аналогичные утверждения справедливы для осей y и z.
Пример: Два человека массами m1 и m2 находятся в лодке массой m3.
В начальный момент времени лодка с людьми находилась в покое.
Определить перемещение лодки, если человек массой m2 пересел к носу лодки на расстояние а.
3. Если в интервале времени [t1, t2] главный вектор внешних сил системы
равен нулю, Re = 0, и в начальный момент скорость центра масс равна нулю,
vC = 0, то радиус-вектор центра масс остается постоянным, rC = const (центр
масс находится в покое – закон сохранения положения центра масс).
4. Если в интервале времени [t1, t2] проекция главного вектора внешних сил
системы на ось x равна нулю, Rxe = 0, и в начальный момент скорость центра
масс по этой оси равна нулю, vCx = 0, то координата центра масс по оси x
остается постоянной, xC = const (центр масс не движется по этой оси).
Аналогичные утверждения справедливы для осей y и z.
1. Объект движения (лодка с людьми):
2. Отбрасываем связи (воду):
3. Заменяем связь реакцией:
4. Добавляем активные силы:
5. Записываем теорему о центре масс:
Проецируем на ось x :
O
Определим на какое расстояние надо пересесть человеку массы m1, чтобы лодка осталась на месте:
Лодка переместится на расстояние l в противоположную сторону.
Слайд 59Лекция 8 (продолжение 8.2)
22
Момент инерции однородного стержня постоянного
сечения относительно оси:
x
z
L
Выделим элементарный
объем
на расстоянии x:
x
dx
Элементарная
масса:
Для вычисления момента инерции относительно центральной
оси (проходящей через центр тяжести) достаточно изменить
расположение оси и задать пределы интегрирования (-L/2, L/2).
Здесь продемонстрируем формулу перехода к параллельным
осям:
zС
5. Момент инерции однородного сплошного цилиндра относительно оси симметрии:
H
dr
r
Выделим элементарный
объем dV = 2πrdrH
(тонкий цилиндр радиуса r) :
Элементарная
масса:
Здесь использована формула объема цилиндра V=πR2H.
Для вычисления момента инерции пустотелого (толстого) цилиндра
достаточно задать пределы интегрирования от R1 до R2 (R2> R1):
6. Момент инерции тонкого цилиндра относительно оси симметрии ( t < H C В силу малости толщины цилиндра То же самое можно получить с использованием формулы для толстостенного цилиндра, учитывая малость t: Поскольку высота цилиндров в результате не входит в формулы моментов инерции, то они остаются справедливыми для тонкого сплошного диска и обода колеса (тонкого кольца). ■ Кинетический момент твердого тела Выделим дискретный малый объем массы Δmi : Или переходя к бесконечно малым: Кинетический момент вращающегося тела равен произведению угловой скорости на момент инерции относительно оси вращения.
считаем, что все точки находятся
на одинаковом расстоянии R до оси
и интегрирования не требуется.
Объем V = 2πRtH. (тонкий цилиндр
радиуса R с толщиной стенки t).
Слайд 60Теорем: Применение теоремы об изменении количества движения системы к движению сплошной
1.Выбираем в качестве объекта движения объем воды, находящийся в криволинейном канале турбины:
2. Отбрасываем связи и заменяем их действие реакциями (Rпов – равнодействующая поверхностных сил)
3. Добавляем активные силы (Rоб – равнодействующая объемных сил):
4. Записываем теорему об изменении количества движения системы:
Количество движения воды в моменты времени t0 и t1
представим как суммы:
Изменение количества движения воды в интервале времени [t0,t1] :
Изменение количества движения воды
за бесконечно малый интервал времени dt: , где
F1
F2
Принимая произведение плотности, площади поперечного сечения и скорости за секундную массу
получаем:
Подставляя дифференциал количества движения системы
в теорему об изменении получаем:
τ
Геометрическая разность векторов секундных количеств движения жидкости равна
сумме главных векторов объемных и поверхностных сил.
19
В проекциях на оси:
Разность проекций векторов секундных количеств движения жидкости на ось равна
сумме проекций главных векторов объемных и поверхностных сил на ту же ось.
Теорема Эйлера





























![Следствия из теоремы о движении центра масс системы(законы сохранения)1. Если в интервале времени [t1, t2]](/img/tmb/4/300643/ba2f6f24e40bed43c667b35a283b4bef-800x.jpg)



![:1. Если в интервале времени [t1, t2] главный вектор внешних сил системы равен нулю, Re](/img/tmb/4/300643/306129367f0887e6ba9aeaea397644c3-800x.jpg)



![Если в интервале времени [t1, t2] вектор главного момента внешних сил системы относительно некоторого центра](/img/tmb/4/300643/df368ee4c4cbcf4973651f15c357bd36-800x.jpg)