МЕХАНИКА
Разделы: Кинематика, Статика, Динамика
Рекомендуемая литература:
1. Мещерский, И. В. «Сборник задач по теоретической механике»
2. Яблонский, А. А. «Сборник задач для курсового проектирования по теоретической механике»
3. Хямяляйнен, В. А. «Теоретическая механика»
4. Тарг, С. М. Краткий курс теоретической механики.
5. Бать, М. И. Теоретическая механика в примерах и задачах. В 2-х т.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретическая механика презентация
Содержание
- 1. Теоретическая механика
- 2. Оформление расчетно-графических работ (РГР) формат A4
- 3. К и н е м а т
- 4. Кинематические характеристики движения точки Т р
- 5. Способы задания движения точки 1. Векторный способ
- 6. Способы задания движения точки б) ускорение точки
- 7. 2. Координатный способ Способы задания движения точки
- 8. Способы задания движения точки б) определение траектории
- 9. Способы задания движения точки в) ускорение точки проекции ускорений точки на оси декартовой системы координат
- 10. Способы задания движения точки 3. Естественный способ
- 11. Способы задания движения точки а) скорость точки
- 12. Способы задания движения точки б) ускорение
- 13. Способы задания движения точки - касательное ускорение,
- 14. Годограф вектора скорости Годограф скорости – это
- 15. Частные случаи движения 1. Равномерное прямолинейное движение
- 16. Пример оформления расчетно - графической работы
- 17. Поступательное движение Поступательным движением твердого тела называется
- 18. Поступательное движение ТЕОРЕМА: Все точки твердого тела,
- 19. Вращательное движение Вращательным движением твердого тела называется
- 20. Вращательное движение Кинематические характеристики вращающегося тела
- 21. Вращательное движение
- 22. Вращательное движение Скорость точки вращающегося тела Скорости
- 23. Ускорение точки вращающегося тела Вращательное движение - вращ.(касат.) ускорение - центростр.(норм.) ускорение
- 24. Вращательное движение Частные случаи вращательного движения
- 25. Сложное движение точки Движение точки M относительно
- 26. Сложное движение точки Теорема сложения скоростей Абсолютная
- 27. Сложное движение точки AB – кулиса движется
- 28. Сложное движение точки Теорема сложения ускорений Абсолютное
- 29. Ускорение Кориолиса Сложное движение точки Ускорение кориолиса
- 30. Правило Жуковского Плоскость П ┴ OZ Сложное движение точки
- 31. Сферическое движение твердого тела
- 32. Сферическое движение твердого тела Углы Эйлера ψ
- 33. Сферическое движение твердого тела ψ= ψ(t) φ=
- 34. Сферическое движение твердого тела Сферическое движение –
- 35. Плоскопараллельное движение твердого тела Плоскопараллельным (плоским) называется
- 36. Плоскопараллельное движение твердого тела Уравнения плоского движения
- 37. Плоскопараллельное движение твердого тела (·) A (полюс)
- 38. Плоскопараллельное движение твердого тела Векторы ω и
- 39. Плоскопараллельное движение твердого тела Определение скоростей точек
- 40. Плоскопараллельное движение твердого тела 2. Теорема о
- 41. Плоскопараллельное движение твердого тела 3. Мгновенный центр
- 42. Плоскопараллельное движение твердого тела Частные случаи определения
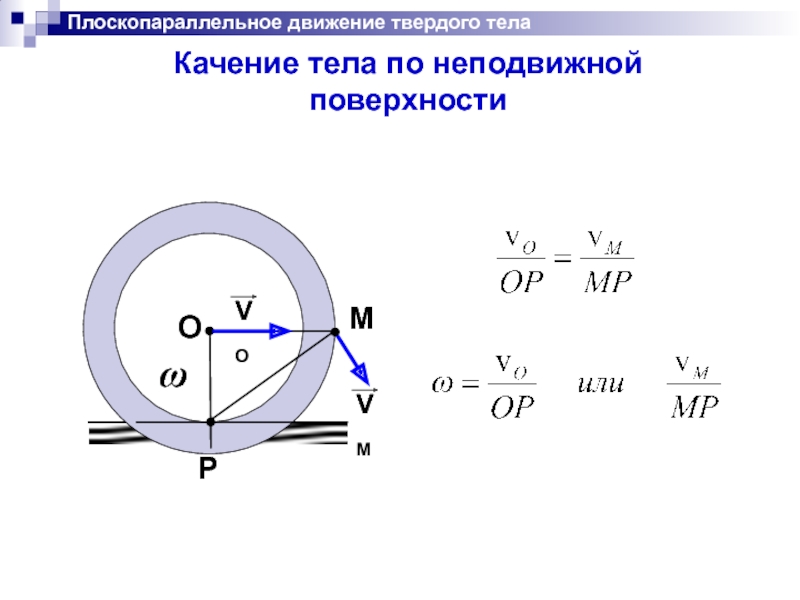
- 43. Плоскопараллельное движение твердого тела Качение тела по неподвижной поверхности
- 44. Плоскопараллельное движение твердого тела Ускорение точки тела
- 45. Плоскопараллельное движение твердого тела - ускорение
- 46. Плоскопараллельное движение твердого тела Мгновенный центр ускорений
- 47. Плоскопараллельное движение твердого тела Частные случаи определения
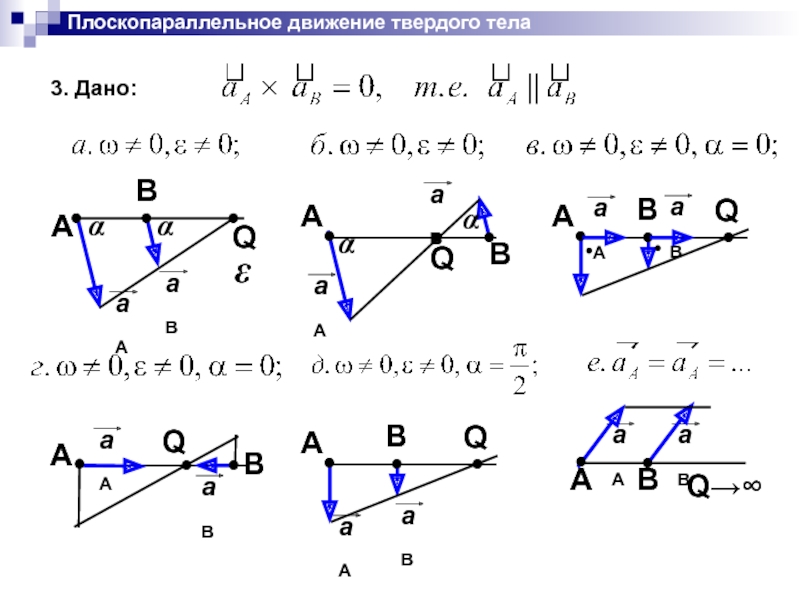
- 48. Плоскопараллельное движение твердого тела 3. Дано:
Оформление расчетно-графических работ (РГР) формат A4 (вертикально) поля: слева - 20 мм, справа, снизу, сверху - 5 мм Штамп (на 1 странице) Расчетно-графические работы для специальностей ГБ, ЭХ, ЭМ
Слайд 1Преподаватель: Зюзин Евгений Александрович Кафедра: Теоретической и геотехнической механики, а.4102 – 4104 ТЕОРЕТИЧЕСКАЯ
Слайд 2Оформление расчетно-графических работ (РГР)
формат A4 (вертикально)
поля: слева - 20 мм, справа,
снизу, сверху - 5 мм
Штамп (на 1 странице)
Расчетно-графические работы для специальностей ГБ, ЭХ, ЭМ
по «сборнику задач…» [2] : К1, К3, С1, Д10
для специальности МА: К1, К3, К7, С3, Д10, Д14 (Д15)
Штамп (на 1 странице)
Расчетно-графические работы для специальностей ГБ, ЭХ, ЭМ
по «сборнику задач…» [2] : К1, К3, С1, Д10
для специальности МА: К1, К3, К7, С3, Д10, Д14 (Д15)
Слайд 3К и н е м а т и к а –
раздел теоретической механики, в котором изучаются геометрические свойства движения тел без учета их масс и действующих на них сил
Механическим движением называется перемещение тела относительно некоторой системы отсчета (системы координат)
Пространство и время в механике считаются абсолютными
Пространство рассматривается как трехмерное евклидово
Время является непрерывно изменяющейся величиной
КИНЕМАТИКА
Слайд 4Кинематические характеристики
движения точки
Т р а е к т о р
и я – геометрическое место последовательных положений движущейся точки в рассматриваемой системе отсчета.
С к о р о с т ь ( ) – векторая величина, определяющая быстроту и направление движения в данной системе отсчета.
У с к о р е н и е ( ) – векторая величина, характеризующая скорость изменения скорости по величине и направлению.
Способы задания
движения точки
В Е К Т О Р Н Ы Й.
К О О Р Д И Н А Т Н Ы Й.
Е С Т Е С Т В Е Н Н Ы Й.
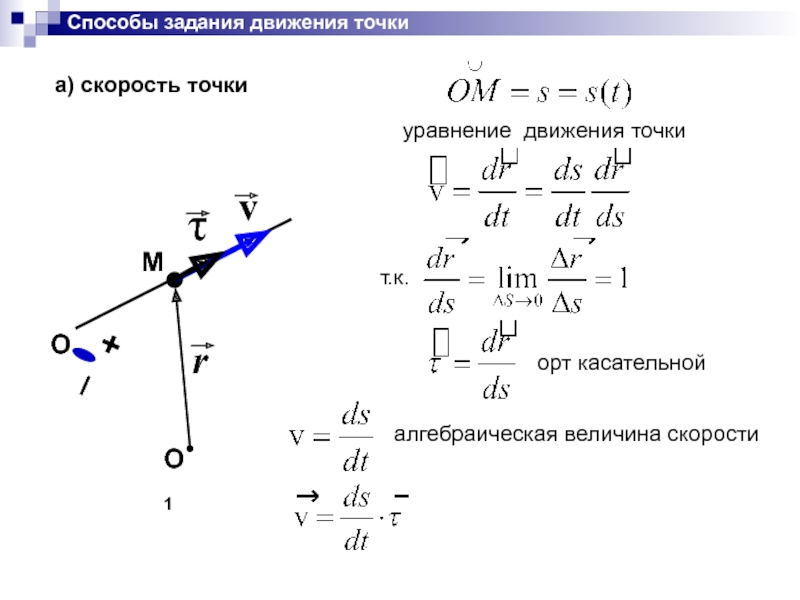
Слайд 5Способы задания движения точки
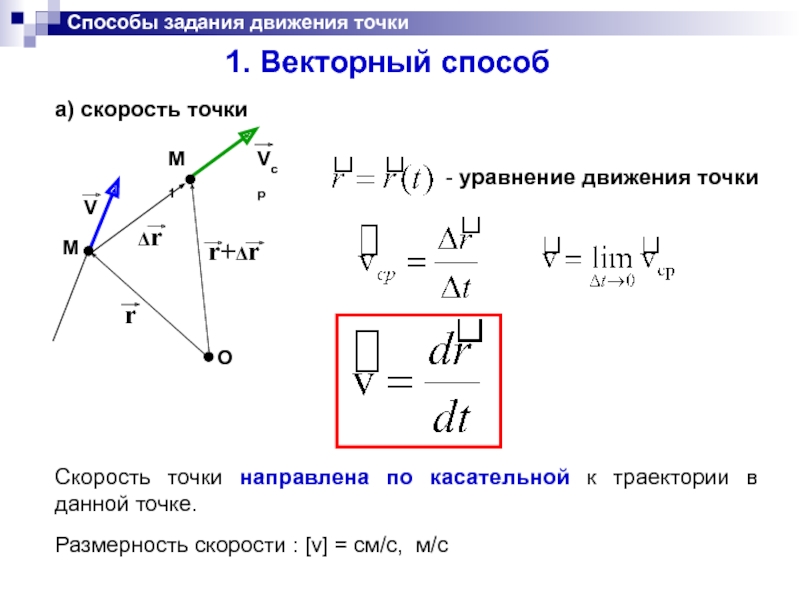
1. Векторный способ
- уравнение движения точки
Скорость точки направлена
по касательной к траектории в данной точке.
Размерность скорости : [v] = см/с, м/с
а) скорость точки
Слайд 6Способы задания движения точки
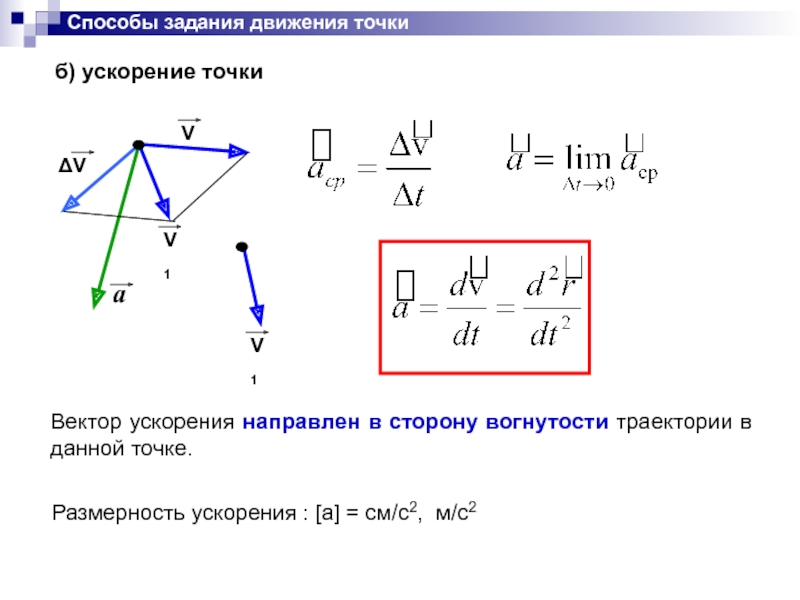
б) ускорение точки
Вектор ускорения направлен в сторону вогнутости
траектории в данной точке.
Размерность ускорения : [a] = см/с2, м/с2
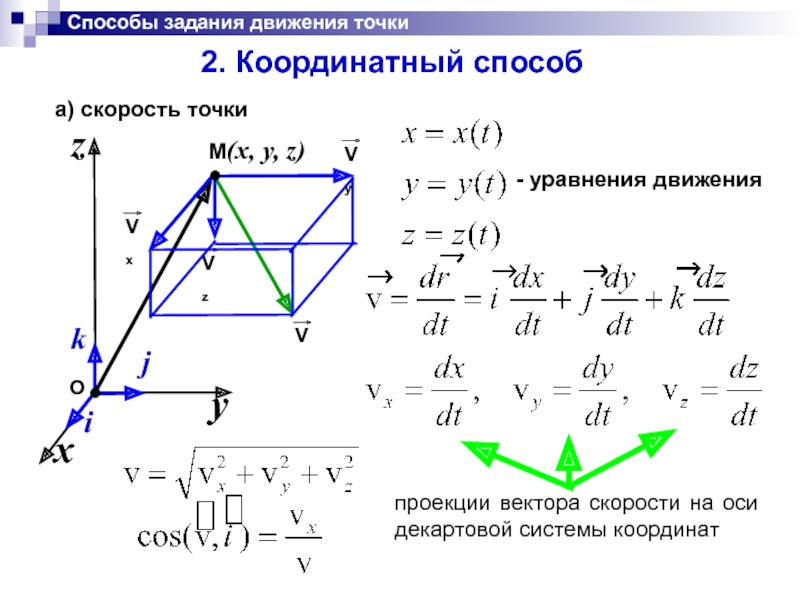
Слайд 72. Координатный способ
Способы задания движения точки
- уравнения движения
проекции вектора скорости на
оси декартовой системы координат
а) скорость точки
Слайд 8Способы задания движения точки
б) определение траектории
Для определения траектории движения точки необходимо
из уравнений движения исключить время (t).
Пример:
Пример:
x
y
Траекторией точки является верхняя часть параболы
Слайд 9Способы задания движения точки
в) ускорение точки
проекции ускорений точки на оси декартовой
системы координат
Слайд 10Способы задания движения точки
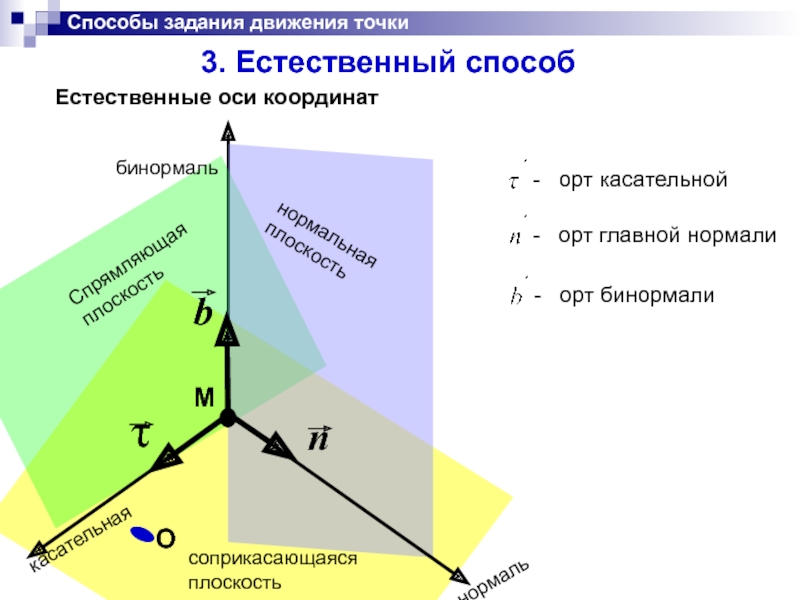
3. Естественный способ
Естественные оси координат
- орт касательной
-
орт главной нормали
- орт бинормали
Слайд 11Способы задания движения точки
а) скорость точки
уравнение движения точки
орт касательной
алгебраическая величина скорости
т.к.
Слайд 12
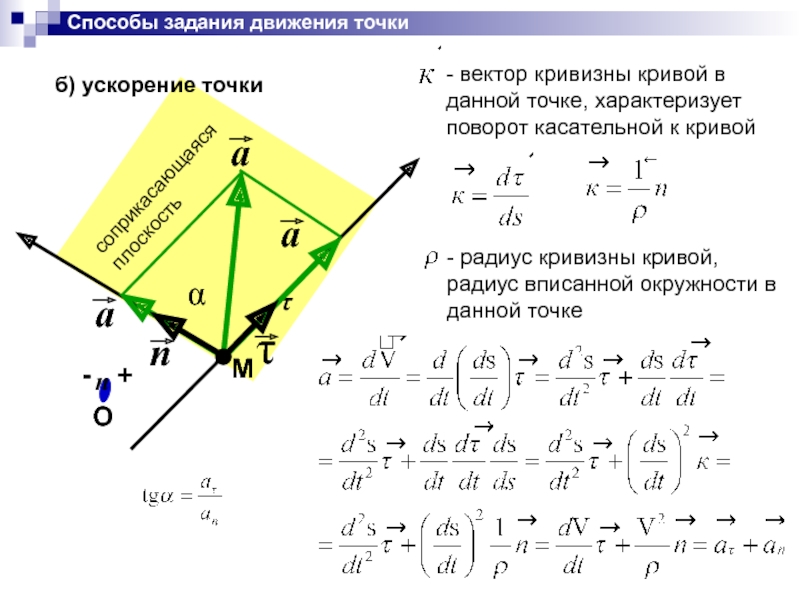
Способы задания движения точки
б) ускорение точки
соприкасающаяся плоскость
М
τ
n
aτ
О
an
a
+
-
α
- радиус кривизны кривой, радиус
вписанной окружности в данной точке
- вектор кривизны кривой в данной точке, характеризует поворот касательной к кривой
Слайд 13Способы задания движения точки
- касательное ускорение, векторная величина, характеризует быстроту изменения
скорости по модулю
- нормальное ускорение, векторная величина, характеризует быстроту изменения скорости по направлению
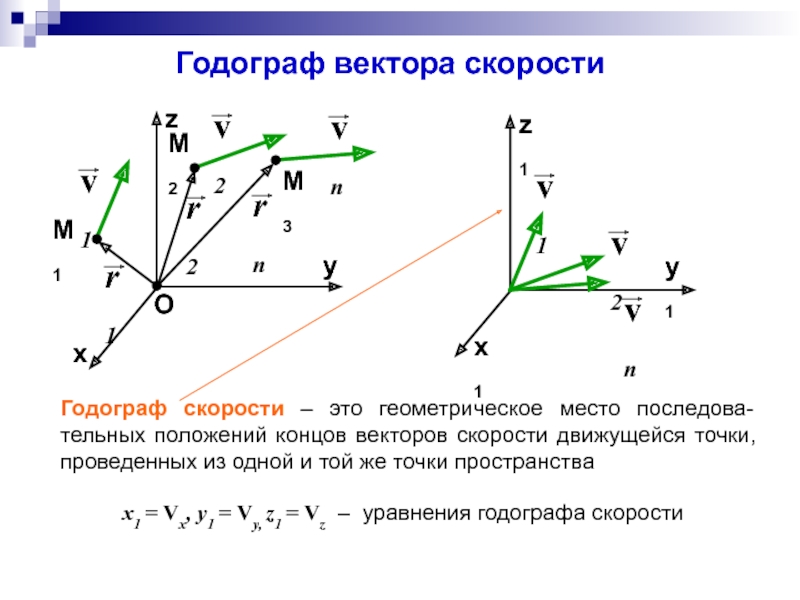
Слайд 14Годограф вектора скорости
Годограф скорости – это геометрическое место последова-тельных положений концов
векторов скорости движущейся точки, проведенных из одной и той же точки пространства
x1 = Vx, y1 = Vy, z1 = Vz – уравнения годографа скорости
Слайд 15Частные случаи движения
1. Равномерное прямолинейное движение
2. Равномерное криволинейное движение
3. Неравномерное прямолинейное
движение
4. Равнопеременное движение
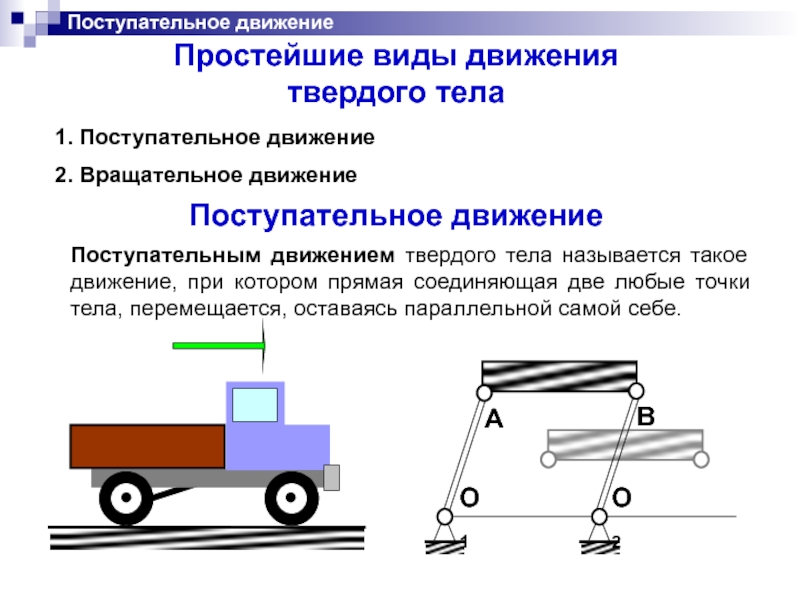
Слайд 17Поступательное движение
Поступательным движением твердого тела называется такое движение, при котором прямая
соединяющая две любые точки тела, перемещается, оставаясь параллельной самой себе.
Простейшие виды движения
твердого тела
1. Поступательное движение
2. Вращательное движение
Поступательное движение
Слайд 18Поступательное движение
ТЕОРЕМА: Все точки твердого тела, движущегося поступательно, описывают одинаковые траектории
и в каждый момент времени имеют одинаковые скорости и ускорения .
Слайд 19Вращательное движение
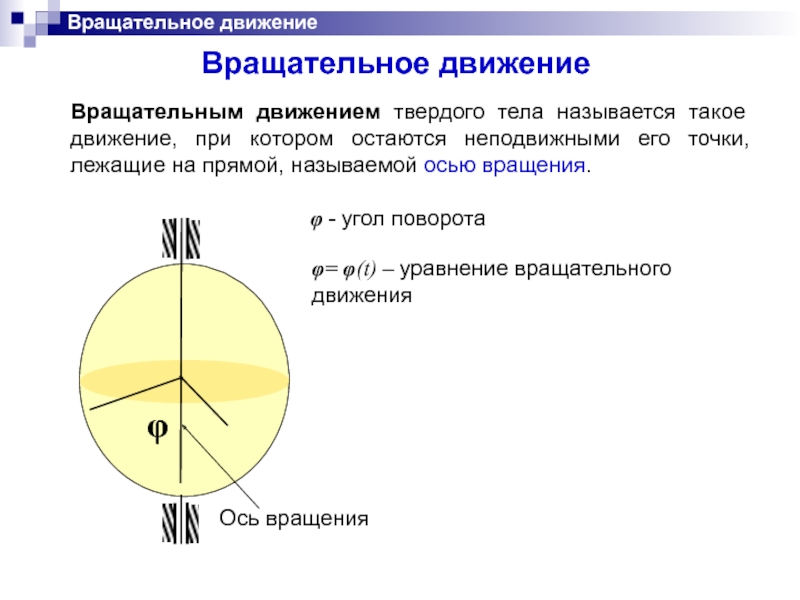
Вращательным движением твердого тела называется такое движение, при котором остаются
неподвижными его точки, лежащие на прямой, называемой осью вращения.
φ - угол поворота
φ= φ(t) – уравнение вращательного движения
Вращательное движение
Слайд 20Вращательное движение
Кинематические характеристики
вращающегося тела
ω – угловая скорость тела
- вектор, характеризующий
быстроту изменения угла поворота
ε – угловое ускорение тела
- вектор, характеризующий быстроту изменения угловой скорости.
В технике угловая скорость n = об/мин.
Слайд 22Вращательное движение
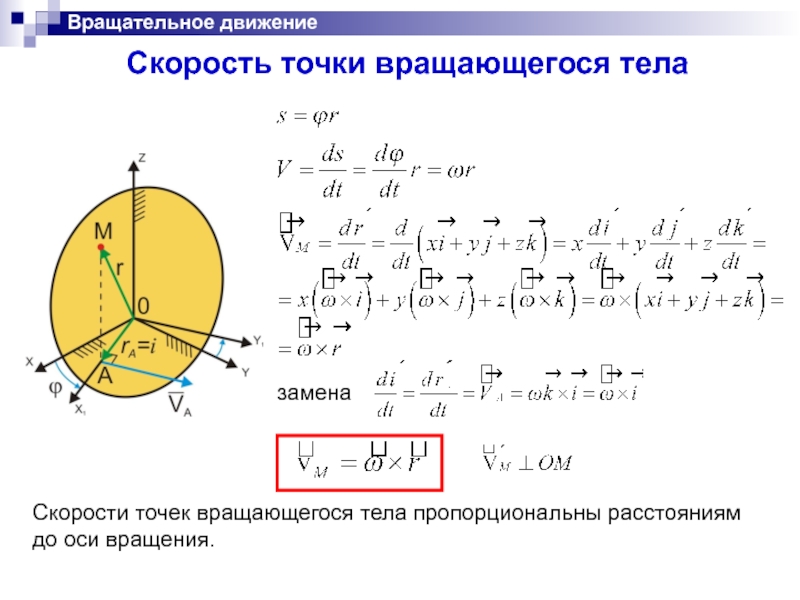
Скорость точки вращающегося тела
Скорости точек вращающегося тела пропорциональны расстояниям до
оси вращения.
замена
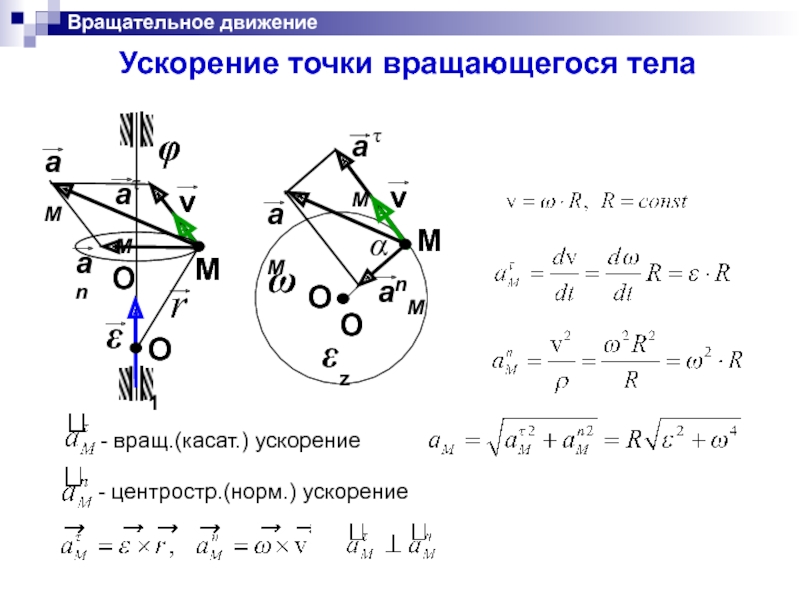
Слайд 23Ускорение точки вращающегося тела
Вращательное движение
- вращ.(касат.) ускорение
- центростр.(норм.) ускорение
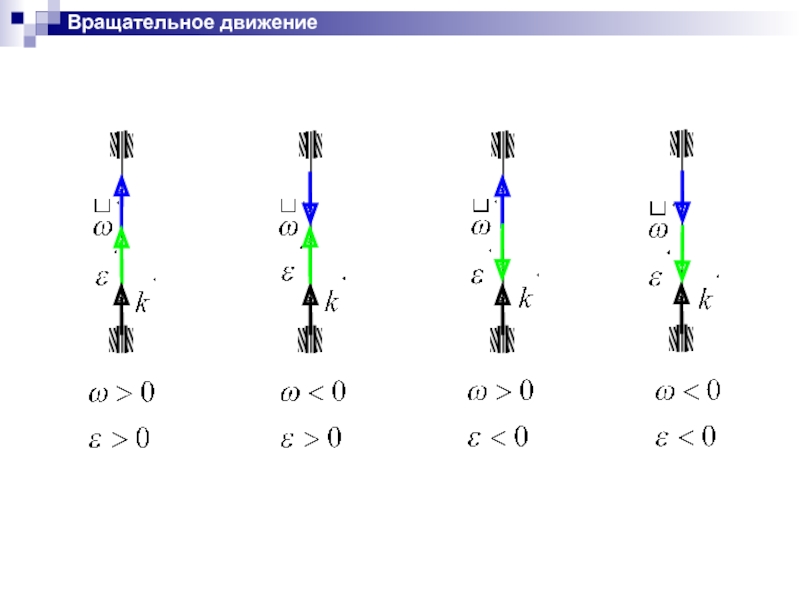
Слайд 24Вращательное движение
Частные случаи вращательного
движения твердого тела
1. Равномерное вращение
2. Равнопеременное вращение
Передача
вращательных движений
ω1
ω2
r1
r2
а) зубчатая (z- кол. зубцов)
б) ременная
Слайд 25Сложное движение точки
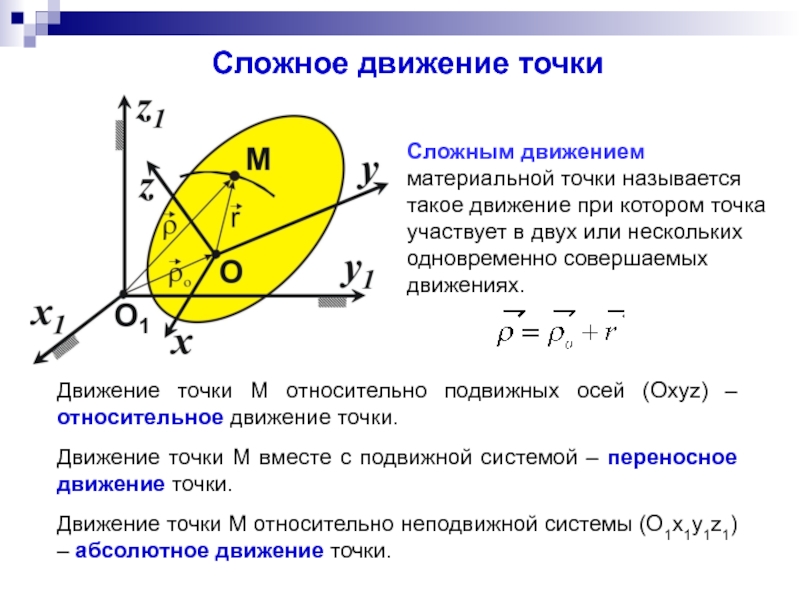
Движение точки M относительно подвижных осей (Oxyz) – относительное
движение точки.
Движение точки M вместе с подвижной системой – переносное движение точки.
Движение точки M относительно неподвижной системы (O1x1y1z1) – абсолютное движение точки.
Движение точки M вместе с подвижной системой – переносное движение точки.
Движение точки M относительно неподвижной системы (O1x1y1z1) – абсолютное движение точки.
Сложным движением материальной точки называется такое движение при котором точка участвует в двух или нескольких одновременно совершаемых движениях.
Слайд 26Сложное движение точки
Теорема сложения скоростей
Абсолютная скорость точки при сложном движении равна
геометрической сумме ее переносной и относительной скоростей.
Слайд 27Сложное движение точки
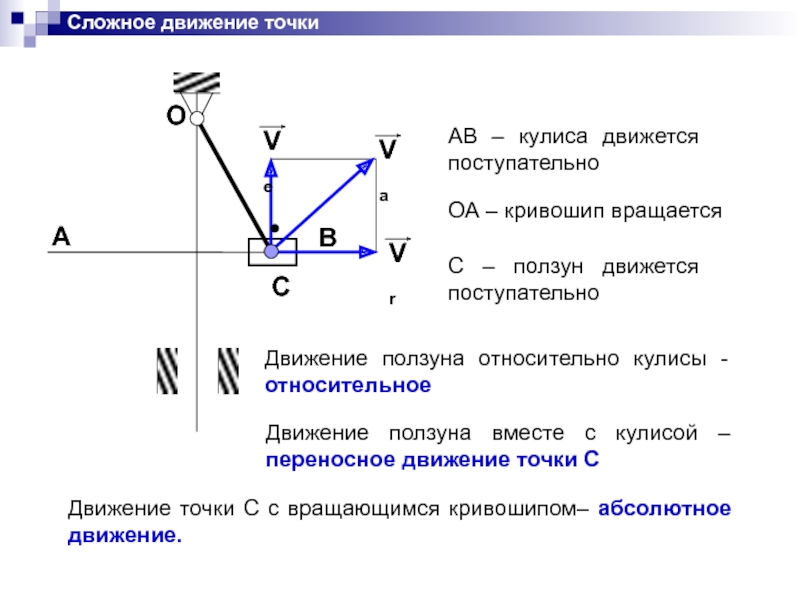
AB – кулиса движется поступательно
ОА – кривошип вращается
С –
ползун движется поступательно
Движение ползуна относительно кулисы - относительное
Движение ползуна вместе с кулисой – переносное движение точки С
Движение точки С с вращающимся кривошипом– абсолютное движение.
Слайд 28Сложное движение точки
Теорема сложения ускорений
Абсолютное ускорение точки при сложном движении равно
геометрической сумме ее переносного, относительного ускорений и кориолисова ускорения.
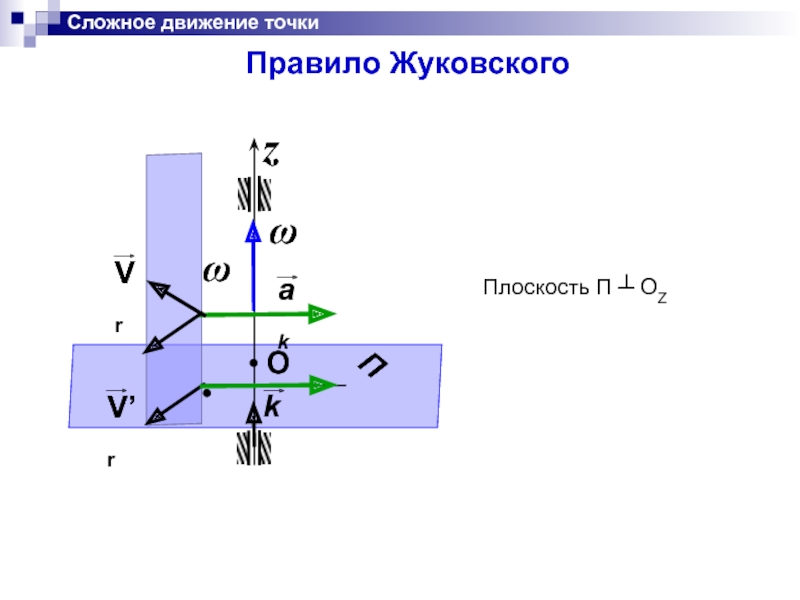
Слайд 29Ускорение Кориолиса
Сложное движение точки
Ускорение кориолиса характеризует совместный эффект вращательного
движения тела
(подвижной среды) и относительного движения точки
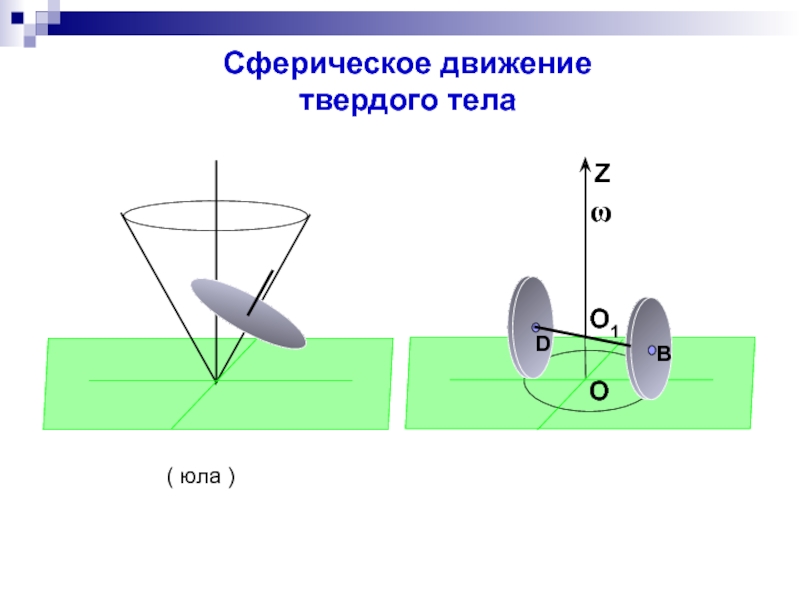
Слайд 32Сферическое движение твердого тела
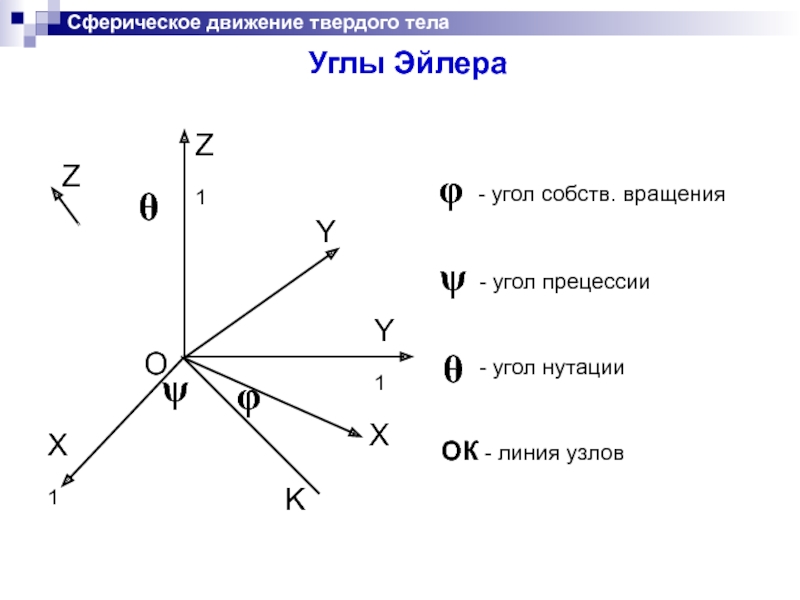
Углы Эйлера
ψ
φ
θ
- угол собств. вращения
- угол прецессии
- угол
нутации
ОК - линия узлов
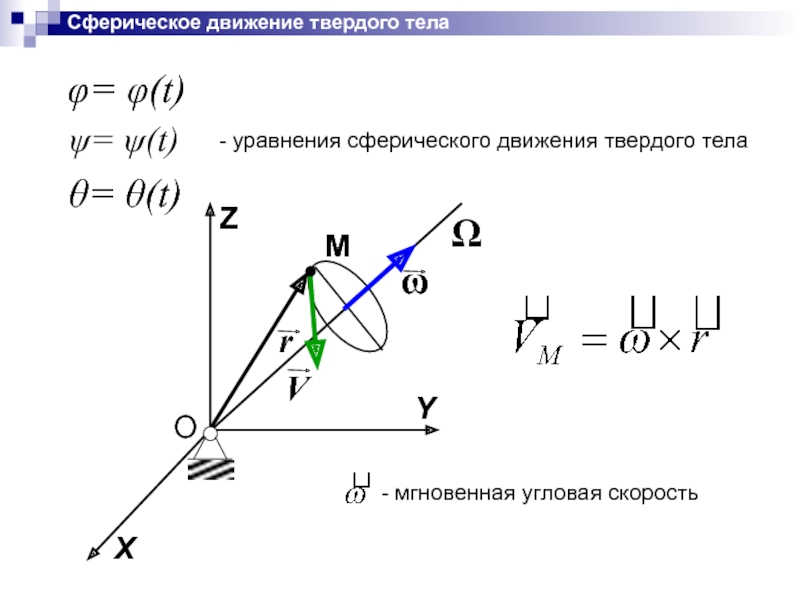
Слайд 33Сферическое движение твердого тела
ψ= ψ(t)
φ= φ(t)
θ= θ(t)
- уравнения сферического движения
твердого тела
- мгновенная угловая скорость
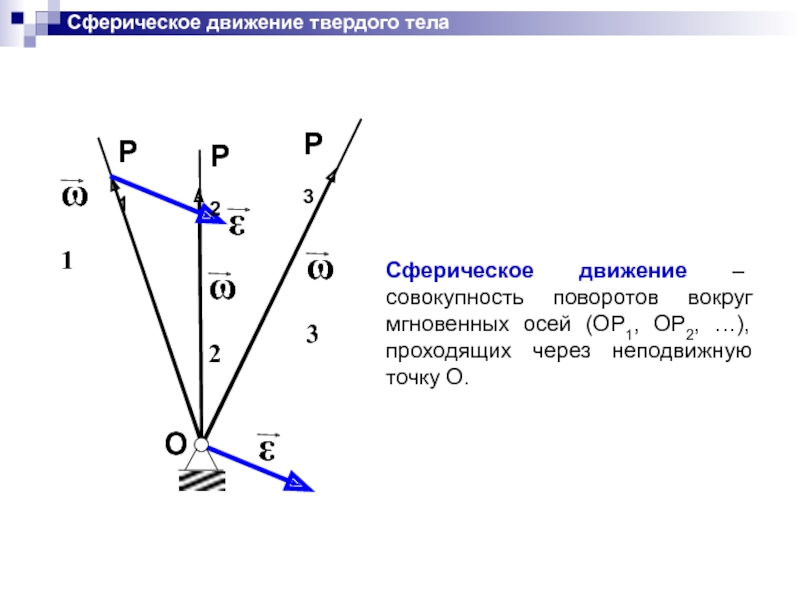
Слайд 34Сферическое движение твердого тела
Сферическое движение – совокупность поворотов вокруг мгновенных осей
(OP1, OP2, …), проходящих через неподвижную точку O.
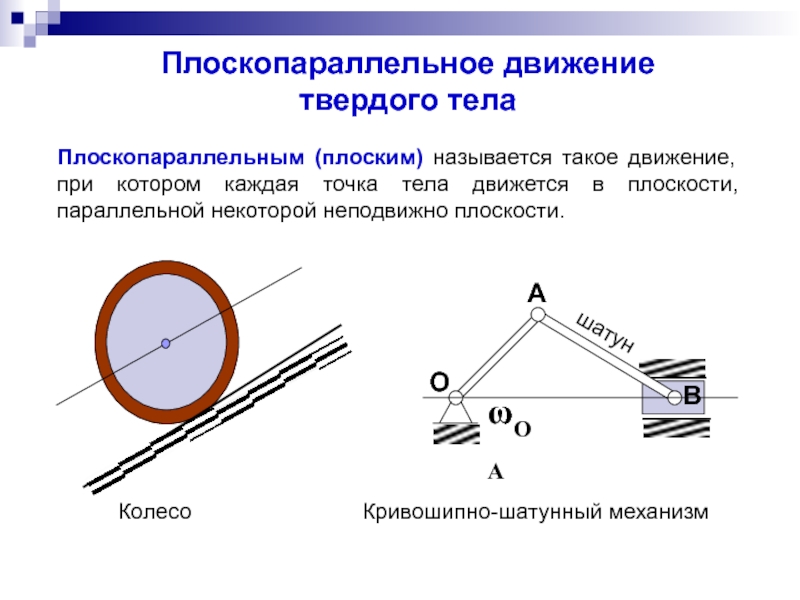
Слайд 35Плоскопараллельное движение
твердого тела
Плоскопараллельным (плоским) называется такое движение, при котором каждая точка
тела движется в плоскости, параллельной некоторой неподвижно плоскости.
Колесо
Кривошипно-шатунный механизм
Слайд 36Плоскопараллельное движение твердого тела
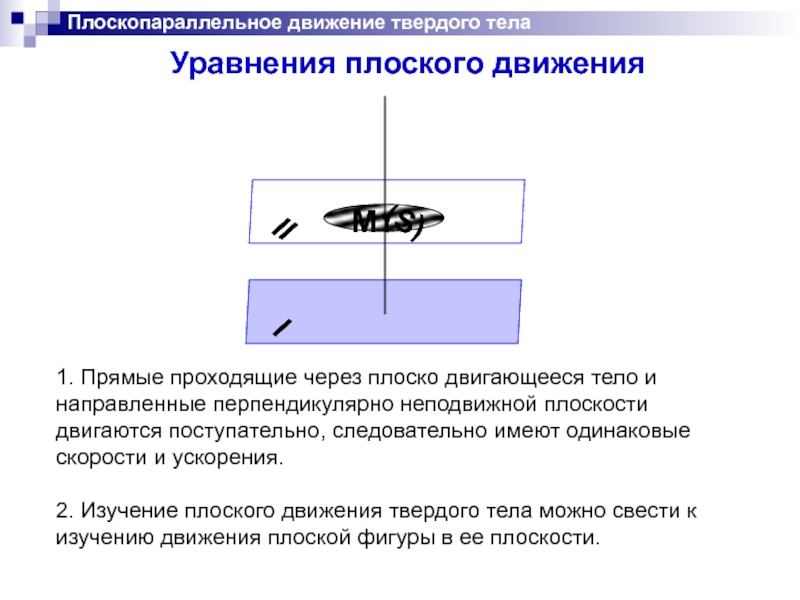
Уравнения плоского движения
1. Прямые проходящие через плоско двигающееся
тело и
направленные перпендикулярно неподвижной плоскости
двигаются поступательно, следовательно имеют одинаковые
скорости и ускорения.
2. Изучение плоского движения твердого тела можно свести к изучению движения плоской фигуры в ее плоскости.
направленные перпендикулярно неподвижной плоскости
двигаются поступательно, следовательно имеют одинаковые
скорости и ускорения.
2. Изучение плоского движения твердого тела можно свести к изучению движения плоской фигуры в ее плоскости.
Слайд 37Плоскопараллельное движение твердого тела
(·) A (полюс) – произвольная точка тела
3. Так
как положение плоской фигуры на ее
плоскости определяется положением двух
ее точек, то движение плоской фигуры можно
изучать как движение прямолинейного
отрезка в этой плоскости.
4. Движение плоской фигуры в ее плоскости
можно разложить на два простейших
движения: поступательное и вращательное.
плоскости определяется положением двух
ее точек, то движение плоской фигуры можно
изучать как движение прямолинейного
отрезка в этой плоскости.
4. Движение плоской фигуры в ее плоскости
можно разложить на два простейших
движения: поступательное и вращательное.
Слайд 38Плоскопараллельное движение твердого тела
Векторы ω и ε – свободные, т.к. вращательное
движение вокруг оси, проходящей через полюс, от выбора полюса не зависит
Слайд 39Плоскопараллельное движение твердого тела
Определение скоростей точек
при плоском движении
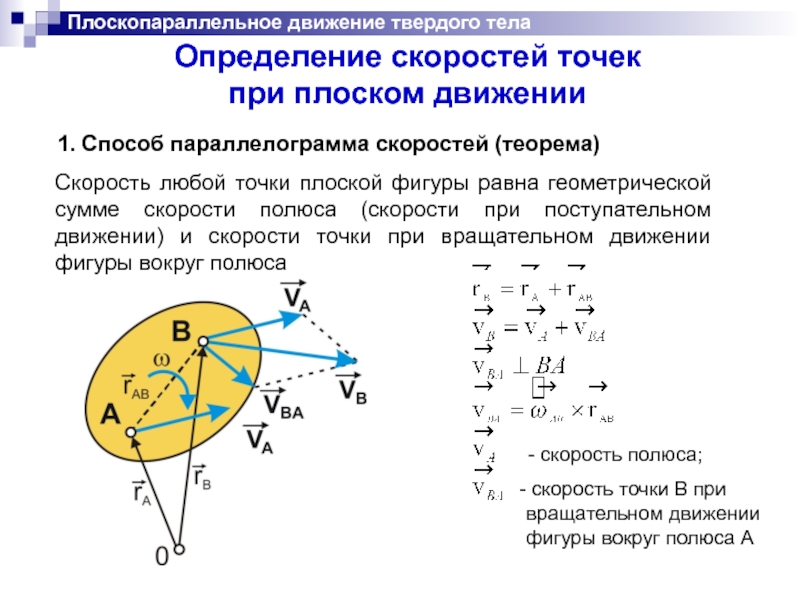
1. Способ параллелограмма скоростей
(теорема)
Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса (скорости при поступательном движении) и скорости точки при вращательном движении фигуры вокруг полюса
- скорость полюса;
скорость точки В при
вращательном движении
фигуры вокруг полюса А
Слайд 40Плоскопараллельное движение твердого тела
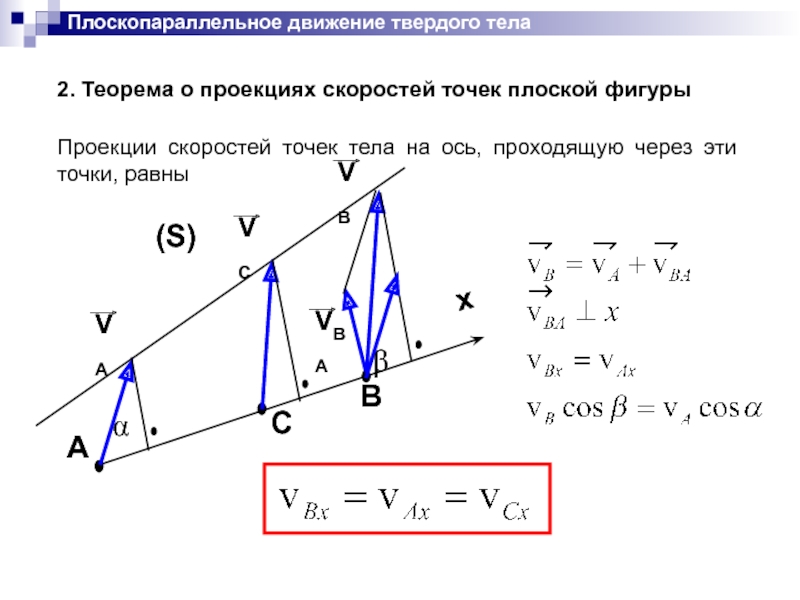
2. Теорема о проекциях скоростей точек плоской фигуры
Проекции скоростей точек тела на ось, проходящую через эти точки, равны
Слайд 41Плоскопараллельное движение твердого тела
3. Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется
точка плоской фигуры, скорость которой в данный момент времени равна нулю (P)
Слайд 42Плоскопараллельное движение твердого тела
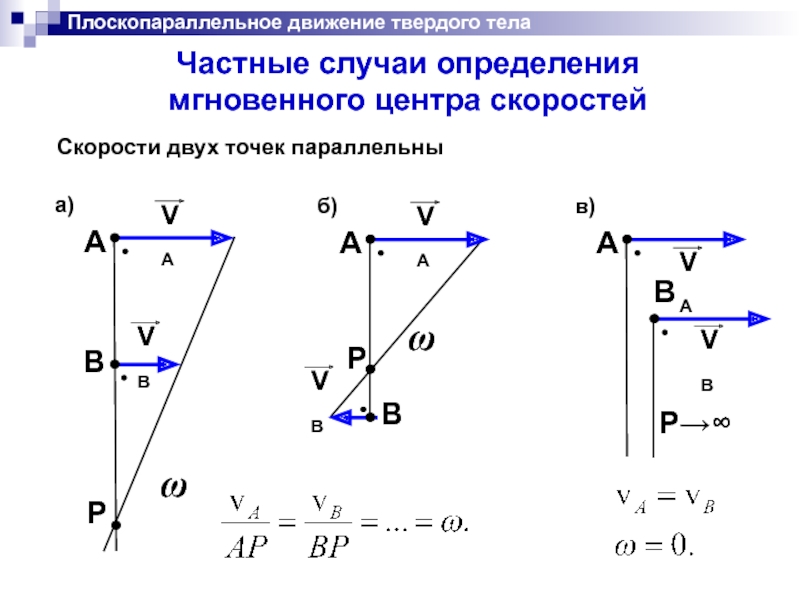
Частные случаи определения
мгновенного центра скоростей
Cкорости двух точек параллельны
a)
б)
в)
Слайд 44Плоскопараллельное движение твердого тела
Ускорение точки тела
при плоском движении
Теорема. Ускорение любой
точки плоской фигуры равно
геометрической сумме ускорения полюса (ускорения при
поступательном движении) и ускорения точки при вращательном
движении фигуры вокруг полюса.
геометрической сумме ускорения полюса (ускорения при
поступательном движении) и ускорения точки при вращательном
движении фигуры вокруг полюса.
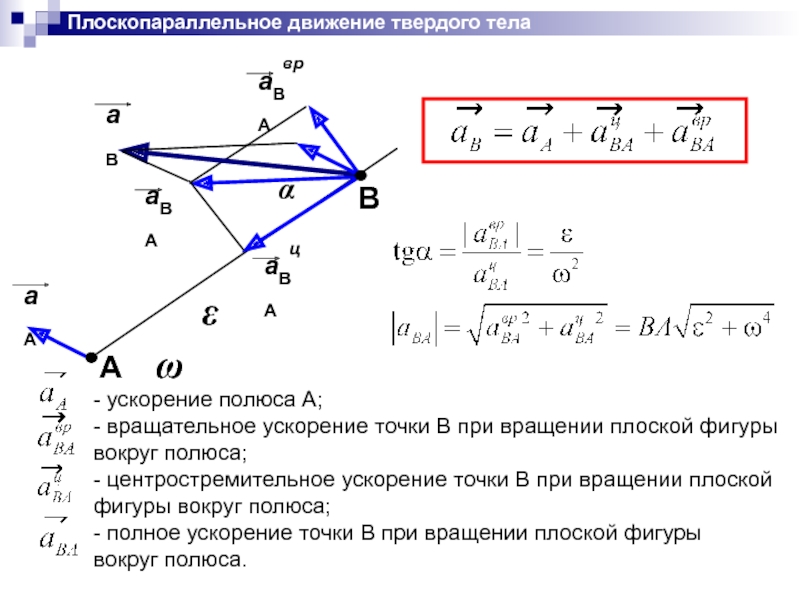
Слайд 45Плоскопараллельное движение твердого тела
- ускорение полюса А;
- вращательное ускорение точки В
при вращении плоской фигуры
вокруг полюса;
- центростремительное ускорение точки В при вращении плоской
фигуры вокруг полюса;
- полное ускорение точки В при вращении плоской фигуры
вокруг полюса.
вокруг полюса;
- центростремительное ускорение точки В при вращении плоской
фигуры вокруг полюса;
- полное ускорение точки В при вращении плоской фигуры
вокруг полюса.
Слайд 46Плоскопараллельное движение твердого тела
Мгновенный центр ускорений
Точка тела, ускорение которой в данный
момент времени равно нулю называется мгновенным центром ускорений (МЦУ) (Q).
Дано:
Доказательство:
Слайд 47Плоскопараллельное движение твердого тела
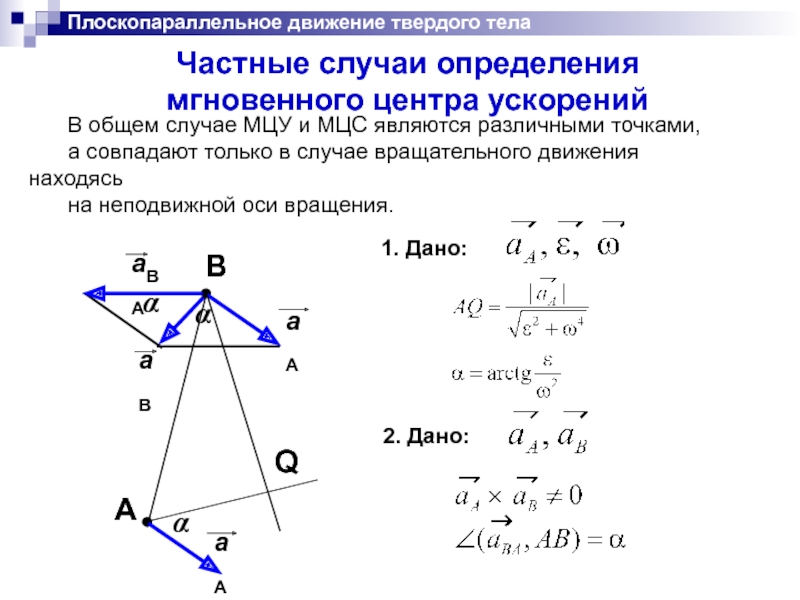
Частные случаи определения
мгновенного центра ускорений
2. Дано:
В общем случае
МЦУ и МЦС являются различными точками,
а совпадают только в случае вращательного движения находясь
на неподвижной оси вращения.
а совпадают только в случае вращательного движения находясь
на неподвижной оси вращения.
1. Дано:
