- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические распределения. (Лекция 2) презентация
Содержание
- 1. Статистические распределения. (Лекция 2)
- 2. Принцип детального равновесия При статистическом описании равновесных
- 3. Функции распределения молекул В статистической физике важное
- 4. Плотность вероятности Функция f(v) называется также плотностью вероятности, поскольку
- 5. Среднее значение физической величины Зная функцию распределения
- 6. Нормировка функции распределения Считается, что для функции распределения f(x) выполняется условие нормировки:
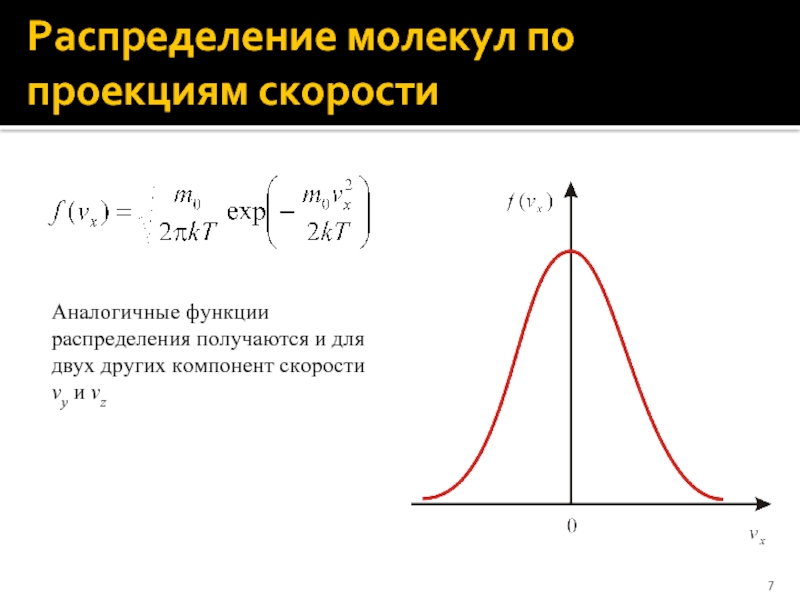
- 7. Распределение молекул по проекциям скорости Аналогичные функции
- 8. Функция распределения f(vx,vy,vz)
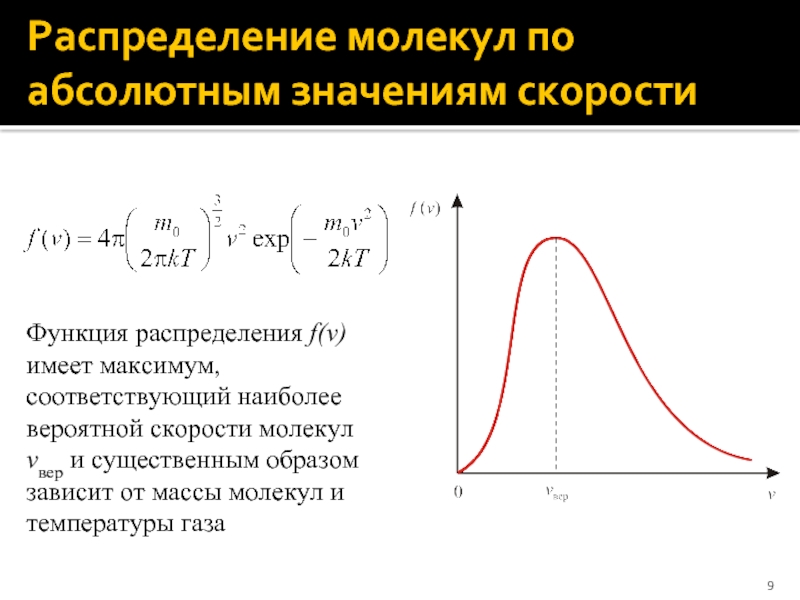
- 9. Распределение молекул по абсолютным значениям скорости Функция
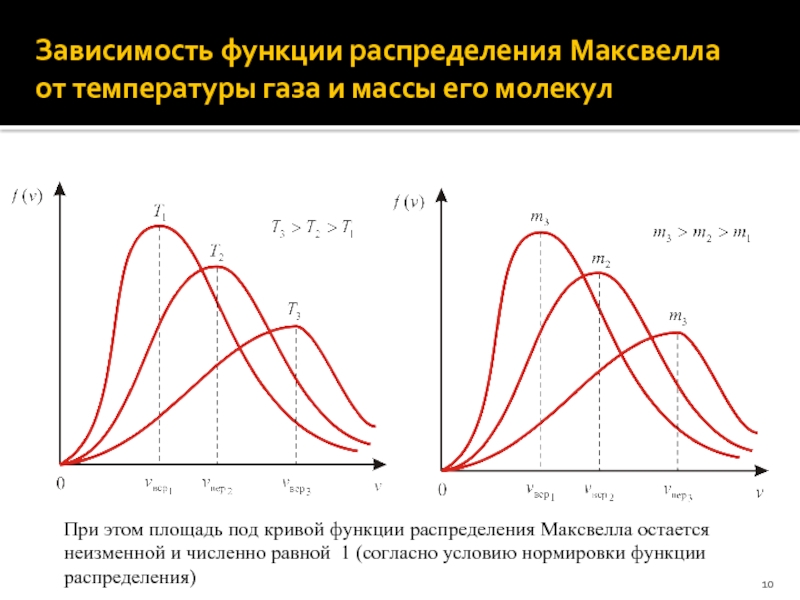
- 10. Зависимость функции распределения Максвелла от температуры газа
- 11. Характерные скорости молекул: наиболее вероятная скорость
- 12. Характерные скорости молекул: средняя скорость
- 13. Характерные скорости молекул: средняя квадратичная скорость
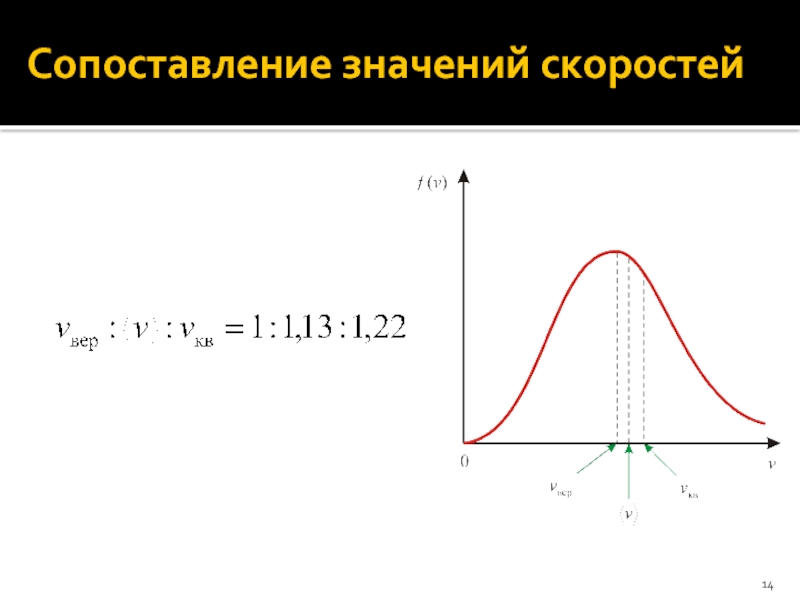
- 14. Сопоставление значений скоростей
- 15. Распределение молекул по величинам безразмерной скорости
- 16. Распределение молекул по значениям импульса
- 17. Распределение молекул по значениям кинетической энергии поступательного движения
- 18. 2.2 Распределение Больцмана ЛЕКЦИЯ 2. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
- 19. Распределение Больцмана Если термодинамическая система, находящаяся в
- 20. Распределение Больцмана Число молекул, находящихся в пределах
- 21. 2.3 Барометрическая формула ЛЕКЦИЯ 2. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
- 22. Барометрическая формула Из распределения Больцмана следует барометрическая
- 23. Предположения, при которых получена барометрическая формула: Воздух
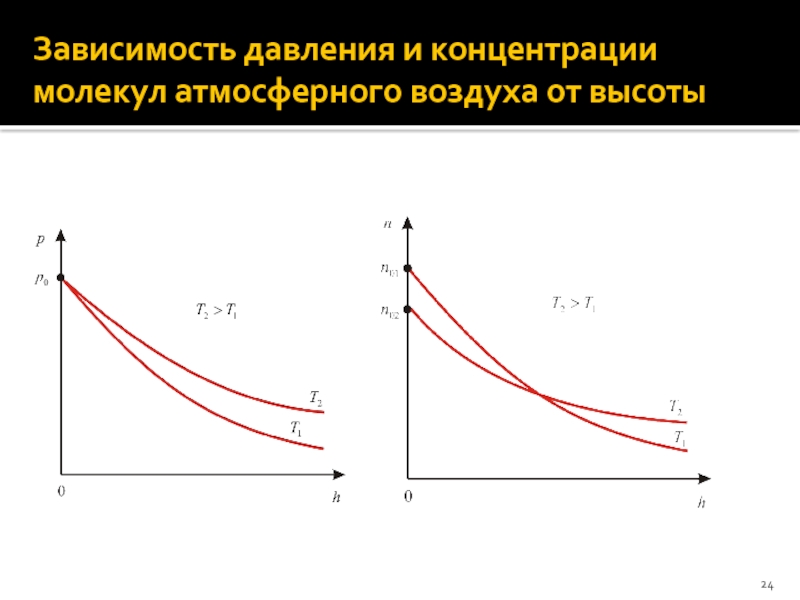
- 24. Зависимость давления и концентрации молекул атмосферного воздуха от высоты
- 25. 2.4 Распределение Максвелла – Больцмана ЛЕКЦИЯ 2. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
- 26. Распределение Максвелла – Больцмана Распределение Максвелла и
- 27. Распределение Максвелла – Больцмана
Принцип детального равновесия При статистическом описании равновесных состояний широко используется принцип детального равновесия: любой микроскопический процесс в равновесной макроскопической системе протекает с той же скоростью, что и обратный ему процесс
Слайд 2Принцип детального равновесия
При статистическом описании равновесных состояний широко используется принцип детального
равновесия: любой микроскопический процесс в равновесной макроскопической системе протекает с той же скоростью, что и обратный ему процесс
Слайд 3Функции распределения молекул
В статистической физике важное значение имеет установление вида функции
распределения молекул по какому-либо параметру: энергии, скорости, импульсу и т.д.
Например, функция распределения молекул по скоростям f(v) определяет вероятность dP(v) того, что скорость молекулы находится в интервале от v до v + dv:
Например, функция распределения молекул по скоростям f(v) определяет вероятность dP(v) того, что скорость молекулы находится в интервале от v до v + dv:
Слайд 5Среднее значение физической величины
Зная функцию распределения молекул f(x) по параметру x,
можно найти среднее значение физической величины ϕ, зависящей от x:
где (a, b) – интервал возможных значений величины x
где (a, b) – интервал возможных значений величины x
Слайд 6Нормировка функции распределения
Считается, что для функции распределения f(x) выполняется условие нормировки:
Слайд 7Распределение молекул по проекциям скорости
Аналогичные функции распределения получаются и для двух
других компонент скорости vy и vz
Слайд 9Распределение молекул по абсолютным значениям скорости
Функция распределения f(v) имеет максимум, соответствующий
наиболее вероятной скорости молекул vвер и существенным образом зависит от массы молекул и температуры газа
Слайд 10Зависимость функции распределения Максвелла от температуры газа и массы его молекул
При
этом площадь под кривой функции распределения Максвелла остается неизменной и численно равной 1 (согласно условию нормировки функции распределения)
Слайд 19Распределение Больцмана
Если термодинамическая система, находящаяся в равновесном состоянии, помещена в силовой
поле, то распределение молекул в пространстве описывается распределением Больцмана:
Здесь n(x, y, z) – концентрация (плотность молекул в точке с координатами x, y, z; Π – потенциальная энергия молекулы в этой точке; n0 – концентрация молекул в том месте, где потенциальная энергия молекулы минимальна (равна нулю)
Здесь n(x, y, z) – концентрация (плотность молекул в точке с координатами x, y, z; Π – потенциальная энергия молекулы в этой точке; n0 – концентрация молекул в том месте, где потенциальная энергия молекулы минимальна (равна нулю)
Слайд 20Распределение Больцмана
Число молекул, находящихся в пределах бесконечно малого объема dV =
dxdydz, расположенного в окрестности точки с координатами x, y, z, определяется выражением
Слайд 22Барометрическая формула
Из распределения Больцмана следует барометрическая формула, описывающая изменение давления атмосферного
воздуха с высотой h:
Здесь p0 – давление у поверхности Земли, M – молярная масса воздуха, g – ускорение свободного падения.
Здесь p0 – давление у поверхности Земли, M – молярная масса воздуха, g – ускорение свободного падения.
Слайд 23Предположения, при которых получена барометрическая формула:
Воздух является идеальным газом, т.е. для
него выполняется уравнение Менделеева – Клапейрона.
Температура воздуха всюду одинакова (атмосфера изотермическая).
g = const, что справедливо для высот, много меньших радиуса Земли.
Температура воздуха всюду одинакова (атмосфера изотермическая).
g = const, что справедливо для высот, много меньших радиуса Земли.
Слайд 26Распределение Максвелла – Больцмана
Распределение Максвелла и распределение Больцмана можно объединить в
одно обобщенное распределение Макселла – Больцмана.
Это распределение позволяет найти число молекул dN, проекции скоростей которых принадлежат интервалам (vx, vx+dvx), (vy, vy+dvy), (vz, vz+dvz) и координаты которых принадлежат области (x, x+dx), (y, y+dy), (z, z+dz)
Это распределение позволяет найти число молекул dN, проекции скоростей которых принадлежат интервалам (vx, vx+dvx), (vy, vy+dvy), (vz, vz+dvz) и координаты которых принадлежат области (x, x+dx), (y, y+dy), (z, z+dz)
