- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Rotation of rigid bodies. Angular momentum and torque. Properties of fluids презентация
Содержание
- 1. Rotation of rigid bodies. Angular momentum and torque. Properties of fluids
- 2. Lecture 4 Rotation of rigid bodies. Angular momentum and torque. Properties of fluids.
- 3. Rotation of Rigid Bodies in General case
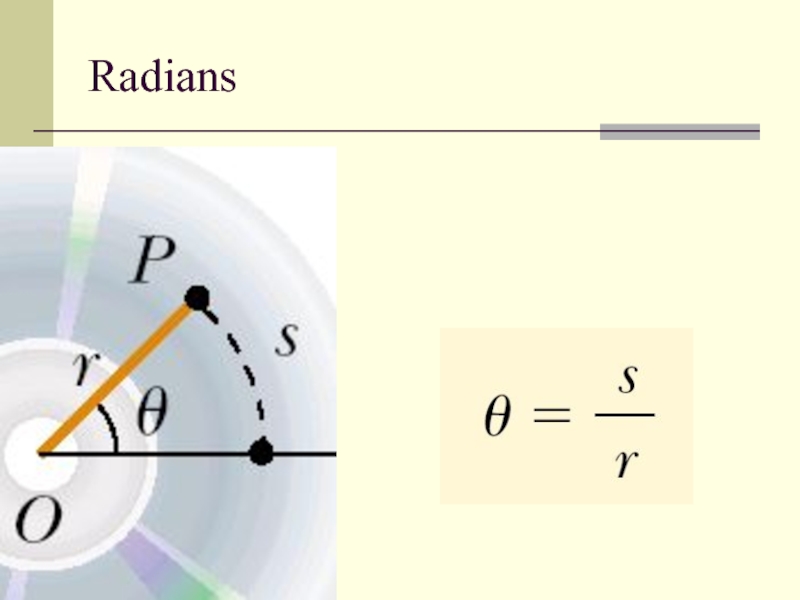
- 4. Radians
- 5. Angular kinematics Angular displacement: Instantaneous angular speed: Instantaneous angular acceleration:
- 6. Angular and linear quantities Every particle of
- 7. Total linear acceleration Tangential acceleration is perpendicular
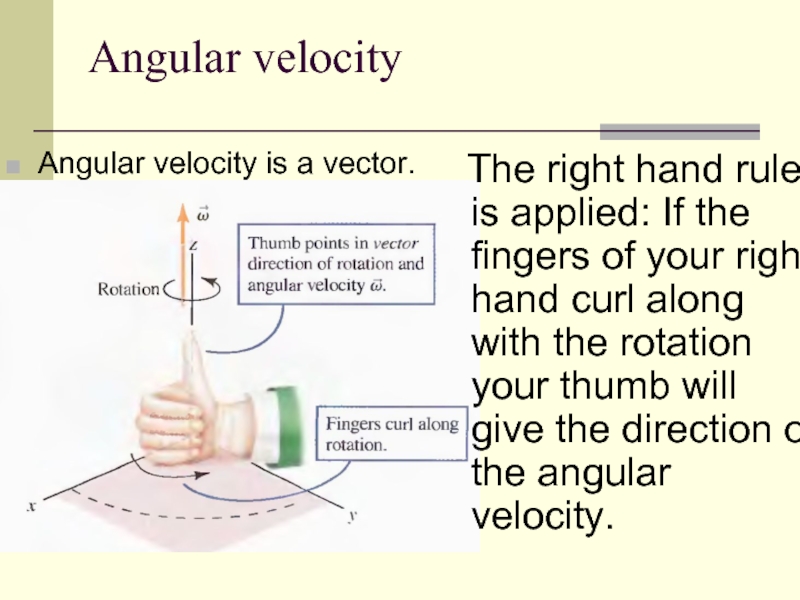
- 8. Angular velocity Angular velocity is a vector.
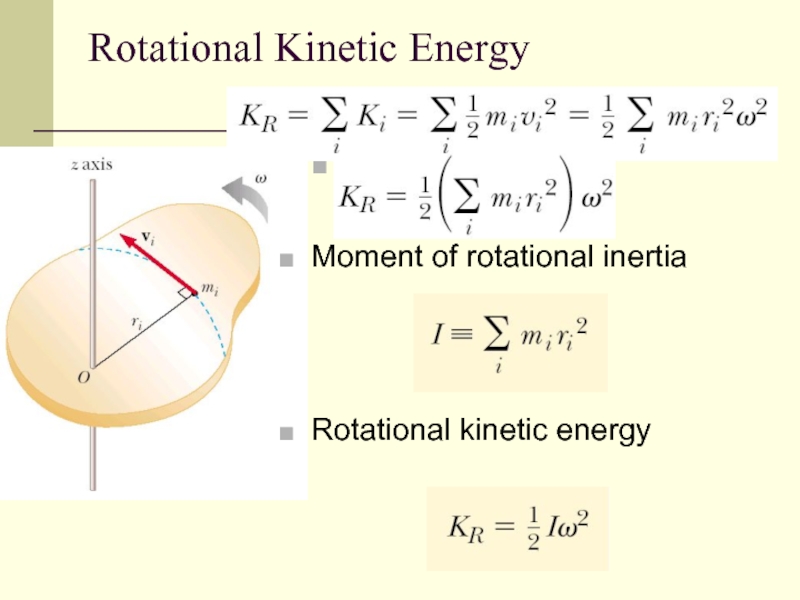
- 9. Rotational Kinetic Energy Moment of rotational inertia Rotational kinetic energy
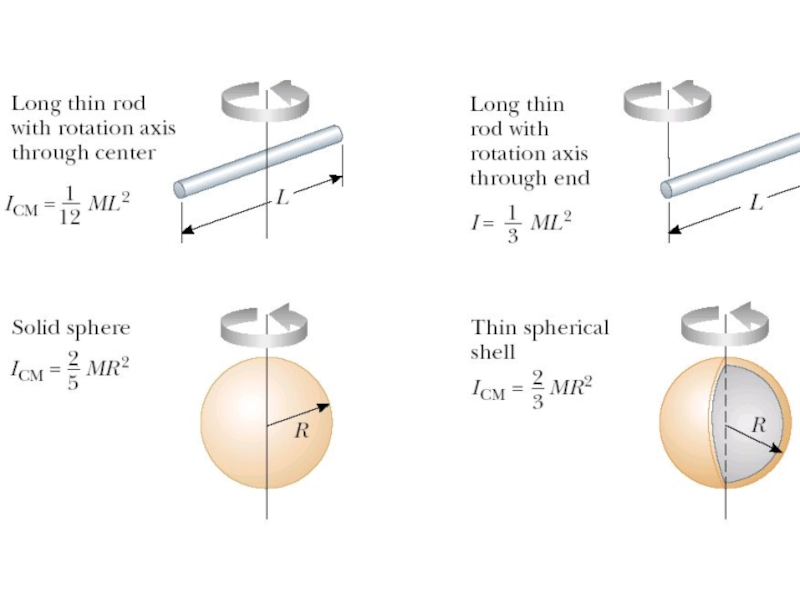
- 10. Calculations of Moments of Inertia
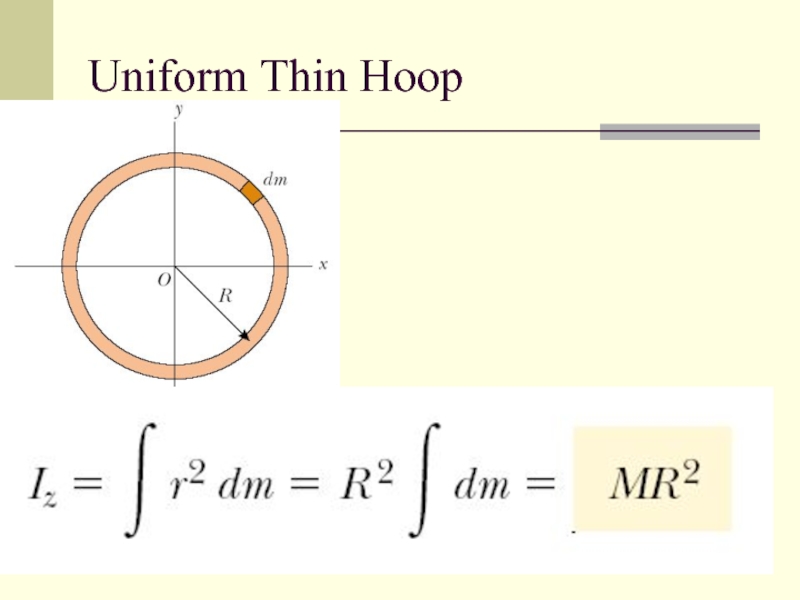
- 11. Uniform Thin Hoop
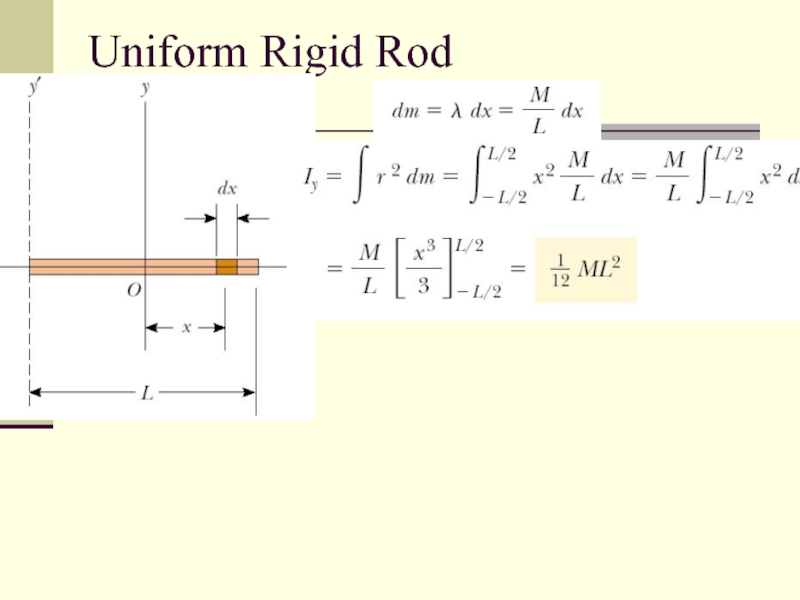
- 12. Uniform Rigid Rod
- 13. Uniform Solid Cylinder
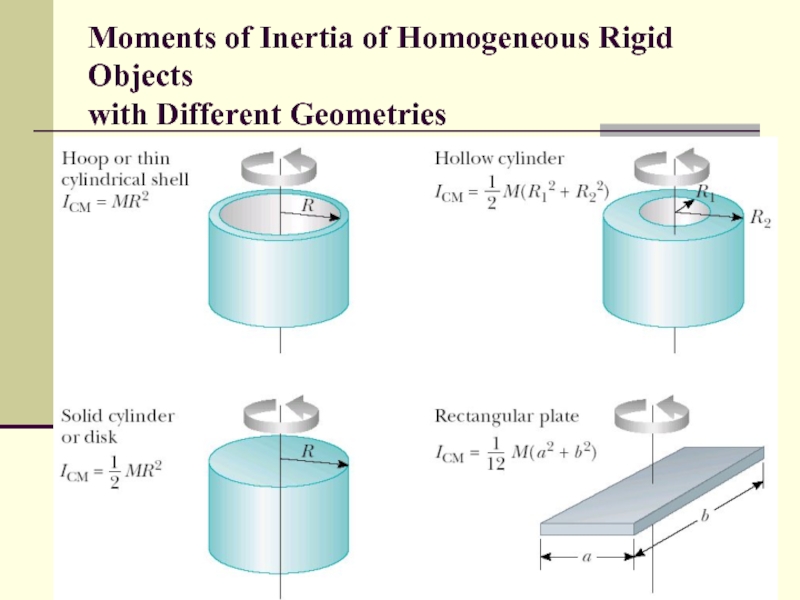
- 14. Moments of Inertia of Homogeneous Rigid Objects with Different Geometries
- 16. Parallel-axis theorem Suppose the moment of inertia
- 18. Torque When a force is exerted on
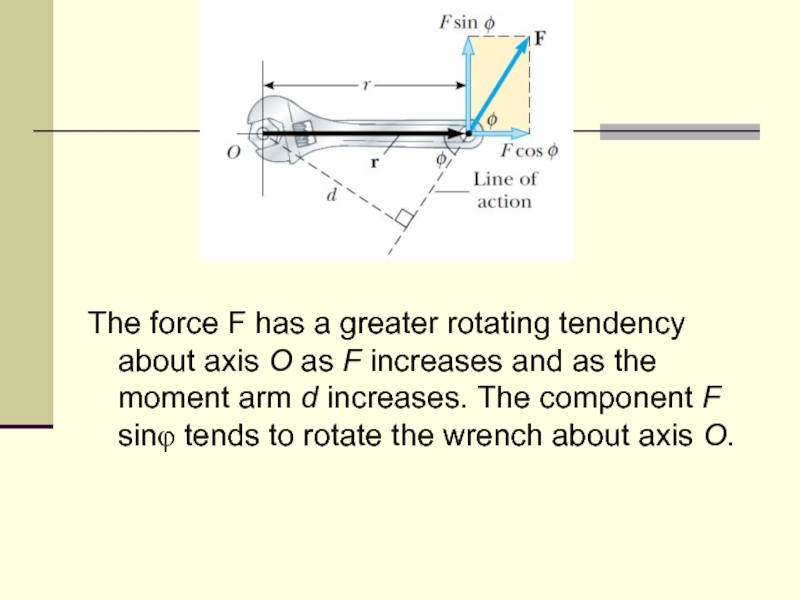
- 19. The force F has a greater
- 20. The force F1 tends to rotate the
- 21. Torque is not Force Torque is not
- 22. Rotational Dynamics Let’s add
- 23. Rotational analogue of Newton’s second law Quantity
- 24. Net External Torque The net external torque
- 25. Angular Momentum of a Rotating Rigid Object
- 26. Angular acceleration
- 27. The Law of Angular Momentum Conservation The
- 28. Change in
- 29. When a rotating skater pulls his hands towards his body he spins faster.
- 30. Three Laws of Conservation for an Isolated
- 31. Work-Kinetic Theory for Rotations Similarly to linear motion:
- 32. The net work done by external
- 33. Equations for Rotational and Linear Motions
- 34. Independent Study for IHW2 Vector multiplication (through
- 35. Fluids Define absolute pressure, gauge pressure, and
- 36. Literature to Independent Study Lecture on Physics
- 37. Problems A solid sphere and a hollow
Слайд 3Rotation of Rigid Bodies in General case
When a rigid object is
Слайд 5Angular kinematics
Angular displacement:
Instantaneous angular speed:
Instantaneous angular acceleration:
Слайд 6Angular and linear quantities
Every particle of the object moves in a
Linear velocity:
Tangential acceleration:
Centripetal acceleration:
Слайд 7Total linear acceleration
Tangential acceleration is perpendicular to the centripetal one, so
Слайд 8Angular velocity
Angular velocity is a vector.
The right hand
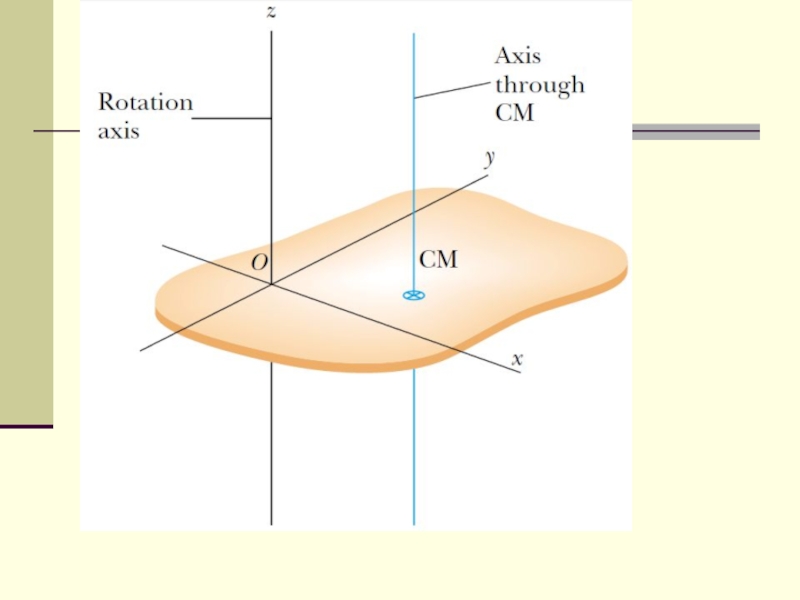
Слайд 16Parallel-axis theorem
Suppose the moment of inertia about an axis through the
Слайд 18Torque
When a force is exerted on a rigid object pivoted about
Слайд 19
The force F has a greater rotating tendency about axis O
Слайд 20 The force F1 tends to rotate the object counterclockwise about O,
We use the convention that the sign of the torque resulting from a force is positive if the turning tendency of the force is counterclockwise and is negative if the turning tendency is clockwise. Then
The force F1 tends to rotate the object counterclockwise about O, and F2 tends to rotate it clockwise.
Слайд 21Torque is not Force
Torque is not Work
Torque should not be confused
Do not confuse torque and work, which have the same units but are very different concepts.
Слайд 23Rotational analogue of Newton’s second law
Quantity L is an instantaneous angular
The torque acting on a particle is equal to the time rate of change of the particle’s angular momentum.
Слайд 24Net External Torque
The net external torque acting on a system about
Слайд 25Angular Momentum of a Rotating Rigid Object
Angular momentum for each particle
Angular momentum for the whole object:
Thus:
Слайд 27The Law of Angular Momentum Conservation
The total angular momentum of a
Слайд 28
Change in internal structure of a rotating body can result in
Слайд 30Three Laws of Conservation for an Isolated System
Full mechanical energy, linear
Слайд 32
The net work done by external forces in rotating a symmetric
Слайд 34Independent Study for IHW2
Vector multiplication (through their components i,j,k).Right-hand rule of
Elasticity
Demonstrate by example and discussion your understanding of elasticity, elastic limit, stress, strain, and ultimate strength.
Write and apply formulas for calculating Young’s modulus, shear modulus, and bulk modulus. Units of stress.
Слайд 35Fluids
Define absolute pressure, gauge pressure, and atmospheric pressure, and demonstrate by
Pascal’s law.
Archimedes’s law.
Rate of flow of a fluid.
Bernoulli’s equation.
Torricelli’s theorem.
Слайд 36Literature to Independent Study
Lecture on Physics Summary by Umarov. (Intranet)
Fishbane Physics
Serway Physics for Scientists… (Intranet)
Слайд 37Problems
A solid sphere and a hollow sphere have the same mass
What are the units for, are these quantities vectors or scalars:
Angular momentum
Angular kinetic energy
Angular displacement
Tangential acceleration
Angular acceleration
Torque