- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Спин – орбитальная связь презентация
Содержание
- 1. Спин – орбитальная связь
- 2. ЛЕКЦИЯ 17. СПИН – ОРБИТАЛЬНАЯ СВЯЗЬ. А.И. Валишев
- 3. МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ В МНОГОЭЛЕКТРОННОМ АТОМЕ.
- 4. Виды взаимодействий Виды взаимодействий
- 5. МЕТОД САМОСОГЛАСОВАННОГО ПОЛЯ.
- 6. Метод самосогласованного поля. МССП
- 7. Метод самосогласованного поля. МССП
- 8. Метод самосогласованного поля. МССП
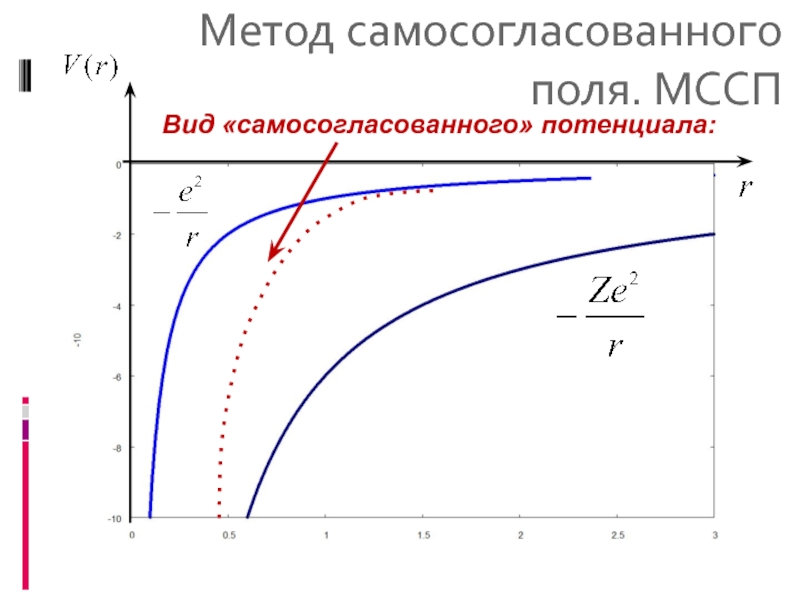
- 9. Метод самосогласованного поля. МССП Вид «самосогласованного» потенциала:
- 10. Метод самосогласованного поля. МССП
- 11. СПИН – ОРБИТАЛЬНОЕ ВЗАИМОДЕЙСТВИЕ.
- 12. Приближение LS связи Спин
- 13. Приближение LS связи Орбитальное
- 14. Приближение LS связи
- 15. Приближение LS связи Состояние
- 16. Приближение LS связи Интегралы
- 17. Приближение LS связи Полный
- 18. Приближение LS связи Полное
- 19. РАСЧЕТ ПОПРАВКИ LS СВЯЗИ.
- 20. Поправка LS связи Оператор LS взаимодействия
- 21. Поправка LS связи Собственные числа оператора (L⋅S)
- 22. Поправка LS связи Осреднение 1/r3 в обкладках радиальных ВФ
- 23. Поправка LS связи Пример. Осреднение 1/r3 для 2p состояния (n=2, l=1)
- 24. Поправка LS связи Окончательно: поправка ΔWLS
- 25. Поправка LS связи Расщепление уровня с
- 26. ОБОЛОЧЕЧНАЯ МОДЕЛЬ.
- 27. Оболочечная модель Оболочки и подоболочки. Квантовые
- 28. Оболочечная модель Подоболочка. Внутри оболочки располагаются
- 29. Оболочечная модель Максимальное число электронов. Максимальное
- 30. Оболочечная модель Число электронов в оболочке
- 31. Оболочечная модель Df. Полностью заполненные оболочки
- 32. ЭЛЕКТРОННЫЕ КОНФИГУРАЦИИ.
- 33. Электронные конфигурации Df.Состояния отдельных электронов в
- 34. ТЕРМ. МУЛЬТИПЛЕТНОСТЬ ТЕРМА.
- 35. Терм Уровни из набора (2L+1)(2S+1) штук,
- 36. Терм Число уровней: Синглетный терм
- 37. Терм Заполненная (замкнутая) оболочка имеет
- 38. Терм Наиболее просто определяются термы электронов
- 39. ПРАВИЛА ХУНДА.
- 40. Правила Хунда Терм при данной конфигурации,
- 41. Правила Хунда Примеры. 1. Конфигурация
- 42. Правила Хунда 2. 3 эквивалентных электрона 3 терма:
- 43. Правила Хунда Результаты справедливы при слабой
- 44. Интернет ресурс
- 45. СПАСИБО ЗА ВНИМАНИЕ ! ЖЕЛАЮ УСПЕХОВ !
Слайд 1КВАНТОВАЯ
И ЯДЕРНАЯ ФИЗИКА
Раздел
АТОМ.
Многоэлектронные атомы.
Спин – орбитальная связь
Абрик Ибрагимович Валишев, к.ф.
? Марлен Еновкович Топчиян , д.ф. -м.н., профессор
Слайд 4Виды взаимодействий
Виды взаимодействий в многоэлектронном атоме
Помимо кулоновского взаимодействия электронов
Кулоновское межэлектронное взаимодействие.
Магнитное взаимодействие электронных токов
Экспериментальные данные: определяющим является электростатическое взаимодействие.
Вырождение в кулоновском центральном поле 1/r снимается учетом межэлектронного взаимодействия
Слайд 6Метод самосогласованного поля. МССП
Попарное взаимодействие электронов учитывается как эффективное
Слайд 7Метод самосогласованного поля. МССП
В отсутствии межэлектронного взаимодействия:
h – одноэлектронный
ψ - многоэлектронная ВФ (волновая функция Хартри)
Результат.
Потенциал самосогласованного поля сферически симметричный потенциал V(r)
2. V(r < a) ~ - Ze2/r, на малых расстояниях
V(r >> a) ~ - e2/r – на больших
Слайд 8Метод самосогласованного поля. МССП
Отношение энергии взаимодействия всех пар электронов
Z(Z-1)/2 штук) к полной энергии взаимодействия электронов с ядром
при одинаковом характерном расстоянии между зарядами:
Слайд 10Метод самосогласованного поля. МССП
Результат.
3. Кулоновское вырождение по орбитальному
В силу сферической симметрии потенциала остается вырождение только по проекции орбитального момента lz
Энергия уровня в атоме становится зависимой от главного квантового числа n и значения орбитального момента l
Слайд 12Приближение LS связи
Спин – орбитальное взаимодействие приближенно моделируется взаимодействием
Классическая модель:
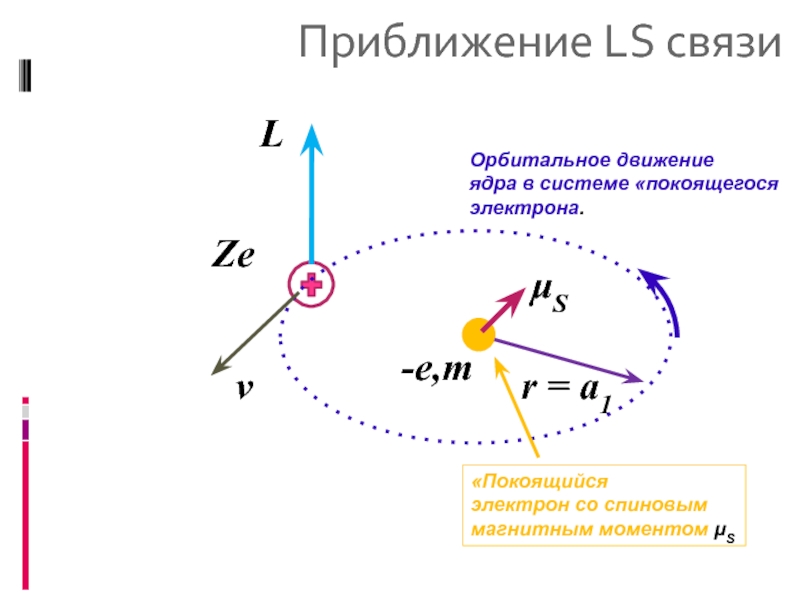
Рассмотрение орбитального движения ядра в системе отсчета электрона. «Ядерным» орбитальным электрическим током создается магнитное поле B, взаимодействующее со спиновым магнитным моментом электрона S
Слайд 13Приближение LS связи
Орбитальное движение
ядра в системе «покоящегося
электрона.
«Покоящийся
электрон со
магнитным моментом μS
Слайд 15Приближение LS связи
Состояние всего набора электронов в атоме приближенно
полного орбитального момента L
полного спинового момента атома S
В силу сферической симметрии
Слайд 16Приближение LS связи
Интегралы движения – J = L +
Квадрат полного орбитального момента L2
Квадрат полного спинового момента S2
Слайд 17Приближение LS связи
Полный орбитальный момент L
не является интегралом
не сохраняется –
т.к. не коммутирует с Гамильтонианом
Полный спиновый момент атома S также
не является интегралом движения –
не сохраняется –
т.к. не коммутирует с Гамильтонианом.
При учете спин орбитальной связи L и S по отдельности не являются интегралами движения .
Уровни энергии в атоме становятся зависимыми
от полного момента импульса J = L + S
Интегралы движения J, L2 , S2 .
Слайд 18Приближение LS связи
Полное число компонент на которое расщепляется уровень
Поправка к уровню энергии при заданных L, S -
Слайд 20Поправка LS связи
Оператор LS взаимодействия в обкладках ВФ с квантовыми числами
Необходимо:
1.определить собственные числа оператора (L⋅S)
2. выполнить осреднение 1/r3
Слайд 25Поправка LS связи
Расщепление уровня с заданными L, S - ΔWLS
δE =
Энергия уровня зависит от L, S сильно,
от J (при заданных L, S) слабо.
Слабая зависимость от J выражается в тонкой структуре атомарных спектров.
Слайд 27Оболочечная модель
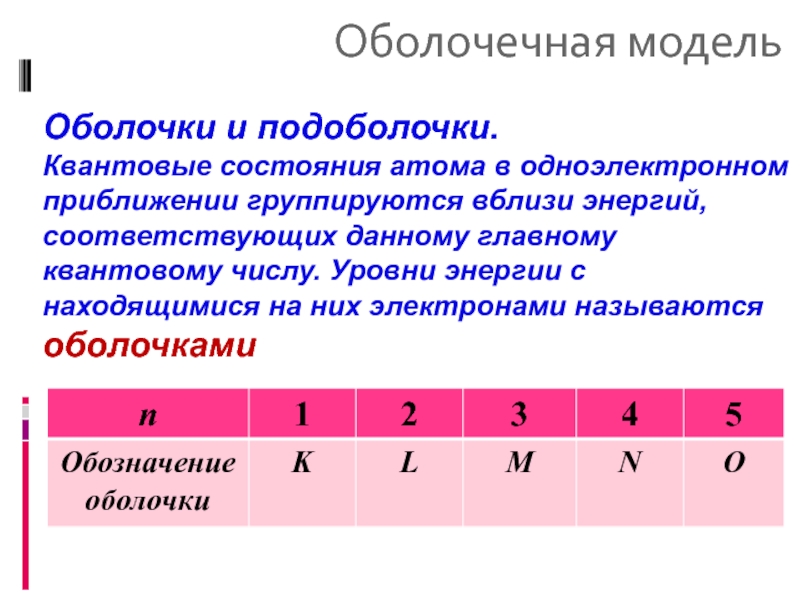
Оболочки и подоболочки.
Квантовые состояния атома в одноэлектронном приближении группируются вблизи
Слайд 28Оболочечная модель
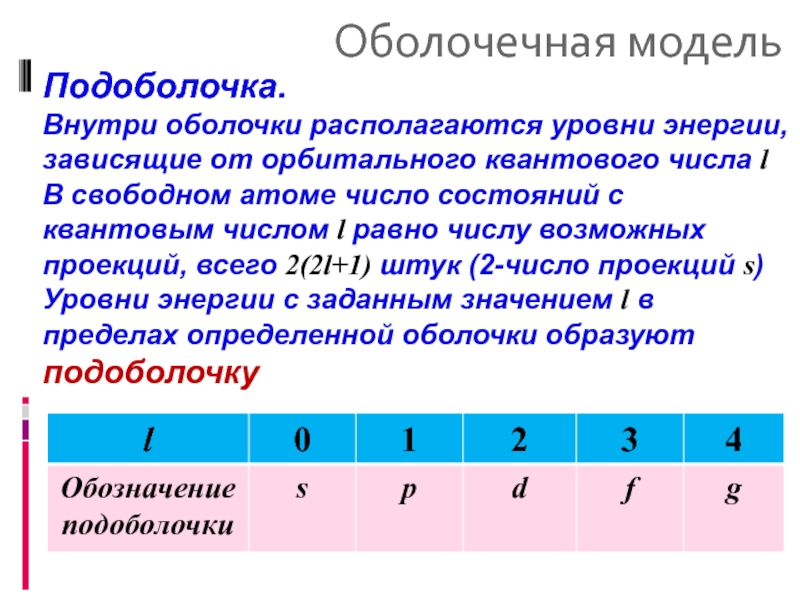
Подоболочка.
Внутри оболочки располагаются уровни энергии, зависящие от орбитального квантового числа
В свободном атоме число состояний с квантовым числом l равно числу возможных проекций, всего 2(2l+1) штук (2-число проекций s)
Уровни энергии с заданным значением l в пределах определенной оболочки образуют подоболочку
Слайд 29Оболочечная модель
Максимальное число электронов.
Максимальное число электронов в подоболочке - 2(2l+1)
Квантовое число
Максимальное число электронов в оболочке
Множитель 2 – число проекций спина
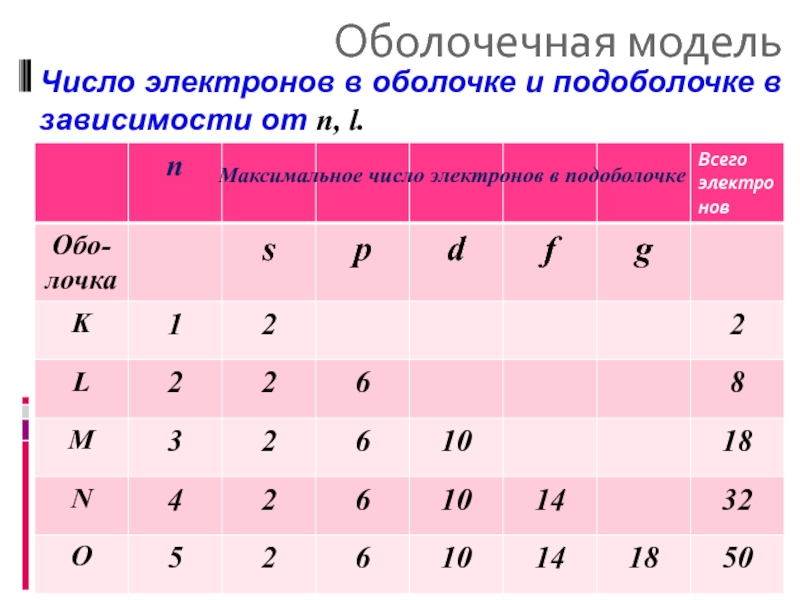
Слайд 30Оболочечная модель
Число электронов в оболочке и подоболочке в зависимости от n,
Максимальное число электронов в подоболочке
Слайд 31Оболочечная модель
Df. Полностью заполненные оболочки называются замкнутыми.
Электроны замкнутых оболочек слабо
Df. Электроны незаполненных оболочек называются валентными.
Взаимодействие валентных электронов с электронами других атомов приводит к образованию устойчивых химических соединений.
Слайд 33Электронные конфигурации
Df.Состояния отдельных электронов в атоме обозначаются символами n l y
Примеры. 1.Электронная конфигурация основного состояния атома Na: 1s2 2s2 2p6 3s
2. Основное состояние атома N: 1s2 2s2 2p3
Df. Все электроны определенной подоболочки называются эквивалентными.
Пример. ns2, nd5, nf12
Слайд 35Терм
Уровни из набора (2L+1)(2S+1) штук, принад-лежащие определенной электронной конфи-гурации с заданными
Обозначения термов
Символьные обозначения термов
Число 2S+1 называется мультиплетностью терма
Слайд 37Терм
Заполненная (замкнутая) оболочка имеет
L = 0 и S = 0.
Основное состояние атома с заполненными оболочками соответствует терму 1S0
Вклад в L и S атома происходит от электронов на незаполненных оболочках
Слайд 38Терм
Наиболее просто определяются термы электронов на незаполненных оболочках с различными n,
Пример. Термы 2-х н.э. электронов 1) np + 2) nf электронов.
Слайд 40Правила Хунда
Терм при данной конфигурации, соответствующий наименьшей энергии.
Df. 1. Из всех
При данном S наименьшую энергию имеет терм с наибольшим значением квантового числа орбитального момента L
Df. 2. Полный момент J терма с наименьшей энергией равен: а) J = |L - S|, если оболочка заполнена менее чем наполовину;
б) J = |L + S|, если оболочка заполнена более чем наполовину
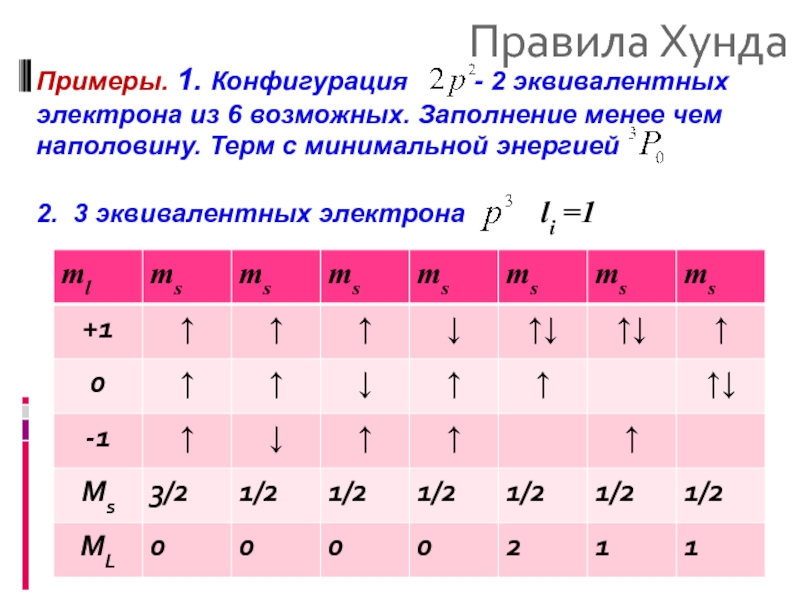
Слайд 41Правила Хунда
Примеры. 1. Конфигурация - 2 эквивалентных
2. 3 эквивалентных электрона li =1
Слайд 43Правила Хунда
Результаты справедливы при слабой L, S связи.
Расстояние между подуровнями тонкой
Противоположный предельный случай – спин орбитальное взаимодействие велико по сравнению с взаимодействием электронов между собой. Приближенно складываются моменты отдельных образуя полный момент электрона j=l+s. В следующем приближении моменты электронов суммируются в полный момент атома. J=Σ j
Связь типа J-J связь.