- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Скорость движения жидкости как сплошной среды презентация
Содержание
- 1. Скорость движения жидкости как сплошной среды
- 2. Лекция 4 Плоское потенциальное движение
- 3. Скорость движения жидкости как сплошной среды Также,
- 4. Скорость движения жидкости как сплошной
- 5. Скорость движения жидкости как сплошной среды Каждое
- 6. Безвихревое (потенциальное) движение жидкости При безвихревом движении т.е. компонеты вихря будут равны 0
- 7. Безвихревое (потенциальное) движение жидкости При выполнении этих
- 8. Безвихревое (потенциальное) движение жидкости Тогда - проекции
- 9. Безвихревое (потенциальное) движение жидкости При
- 10. При плоском движении траектории всех
- 11. Производная в правой части - это субстанци-ональная
- 12. И уравнение неразрывности для плоского движения Плоскопараллельное движение жидкости
- 13. Для плоского движения потенциал скорости – это
- 14. Решение этой задачи непосредственно связа-но с необходимостью
- 15. При исследовании плоского потенциального движения наряду
- 16. Из уравнений линий тока для такого движения
- 17. х у i
- 18. Плоскопараллельное движение жидкости и рассматривая расход элементарной
- 19. dq= - иуdx+ ихdу. т. е. dq=dψ
- 20. Потенциал скорости и функция тока взаимоза-висимы. Например, откуда Плоскопараллельное движение жидкости
- 21. Потенциал скорости и функции тока Линии тока
- 22. Гидродинамическая сетка имеет большое практическое значение; если
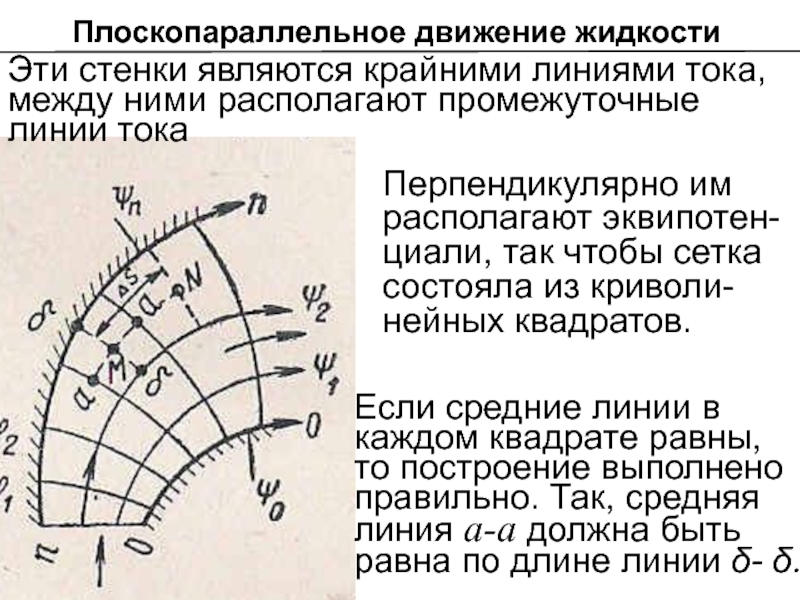
- 23. Эти стенки являются крайними линиями тока, между
- 24. Тогда, пользуясь этой сет-кой, можно приближенно определить
Слайд 3Скорость движения жидкости как сплошной среды
Также, как и при изучении движения
Это отражено в теореме Гельмгольца
Общий случай сложного движения жидкости рассматривается состоящим из движения элементарного объема как квазитвердого тела, скорость которого равна сумме скоро-стей поступательного и вращательного движе-ния, и деформационного движения
Слайд 4
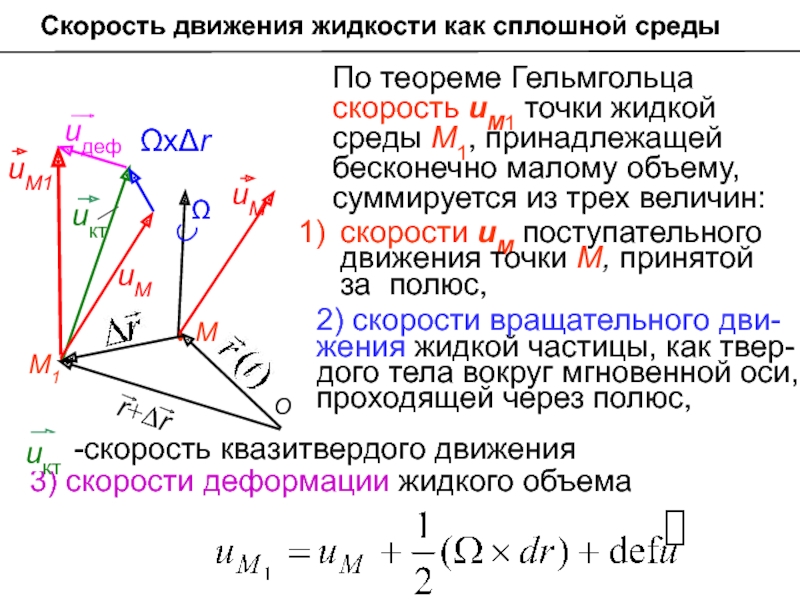
Скорость движения жидкости как сплошной среды
Ω
По теореме Гельмгольца скорость uМ1 точки
скорости uМ поступательного движения точки М, принятой за полюс,
2) скорости вращательного дви-жения жидкой частицы, как твер-дого тела вокруг мгновенной оси, проходящей через полюс,
3) скорости деформации жидкого объема
Слайд 5Скорость движения жидкости как сплошной среды
Каждое составляющее движение рассматрива-лось подробно, так
Рассмотрим теперь частные случаи движений, например, движение при отсутствии вихрей.
Слайд 6Безвихревое (потенциальное) движение жидкости
При безвихревом движении
т.е. компонеты вихря будут равны 0
Слайд 7Безвихревое (потенциальное) движение жидкости
При выполнении этих условий линейное диф-ференциальное выражение
будет
C другой стороны полный дифференциал этой функции
Слайд 8Безвихревое (потенциальное) движение жидкости
Тогда
- проекции скорости являются частными производными функции φ
Эту функцию φ называют потенциалом скоро-стей.
Безвихревое движение называют потенци-альным.
Слайд 9
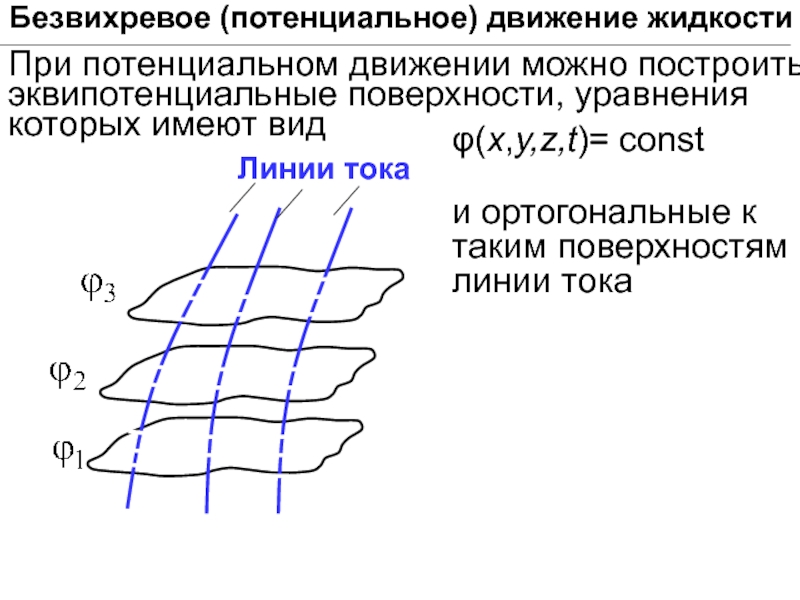
Безвихревое (потенциальное) движение жидкости
При потенциальном движении можно построить эквипотенциальные поверхности, уравнения
φ(х,y,z,t)= сonst
и ортогональные к таким поверхностям линии тока
Слайд 10
При плоском движении траектории всех частиц являются плоскими кривыми.
Дифференциальные уравнения Эйлера
Плоскопараллельное движение жидкости
Движение жидких сред в различных устройст-
вах и машинах (в том числе в насосах и венти-
ляторах) можно считать плоскопараллельным.
Слайд 11Производная в правой части - это субстанци-ональная производная, для плоского движения
Следовательно, уравнения движения выгля-дят следующим образом:
Плоскопараллельное движение жидкости
Слайд 13Для плоского движения потенциал скорости – это функция φ(х,у), для которой
Плоская кривая
φ(х,у)=С
выражается эквипотенциальной линией
Плоскопараллельное движение жидкости
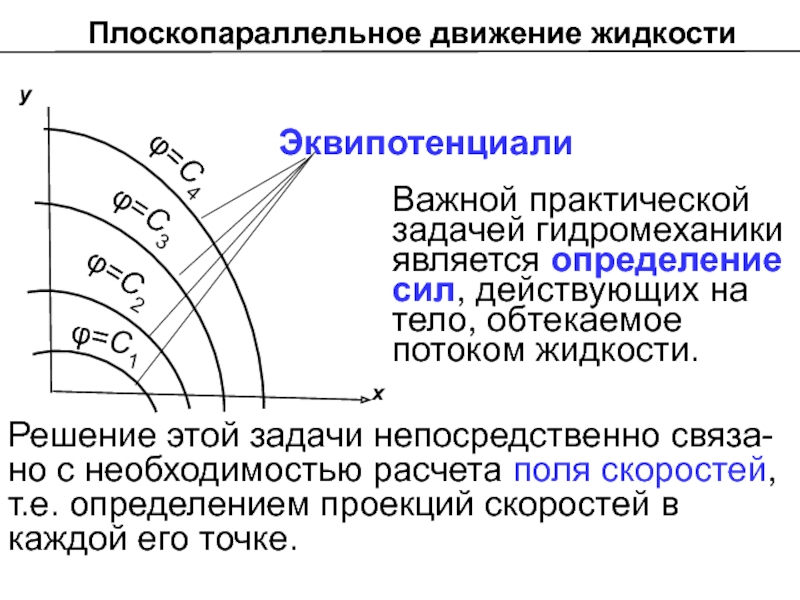
Слайд 14Решение этой задачи непосредственно связа-но с необходимостью расчета поля скоростей, т.е.
Важной практической задачей гидромеханики является определение сил, действующих на тело, обтекаемое потоком жидкости.
Плоскопараллельное движение жидкости
Слайд 15
При исследовании плоского потенциального движения наряду с потенциалом скорости большое значение
Пусть такая функция существует для некото-рого потока. Тогда ее полный дифференциал
Плоскопараллельное движение жидкости
Слайд 16Из уравнений линий тока для такого движения
можно получить
т.е. поле линий
ψ(х,у)=С
Плоскопараллельное движение жидкости
Слайд 17х
у
i
i+1
Δy
yi
Расход жидкости, про-текающий в элемен-тарной струйке между двумя линиями тока
q=u·Δl
или
q=-uу·Δх+uх·Δу
Плоскопараллельное
Рассмотрим движение , представленное семей-ством линий тока
Выделим 2 линии тока i и i+1
Слайд 18Плоскопараллельное движение жидкости
и рассматривая расход элементарной струйки как приращение расхода всего
Переходя к пределу при неограниченном сближении линий тока i и i+1
dq= - иуdx+ ихdу.
Слайд 19dq= - иуdx+ ихdу.
т. е.
dq=dψ
Интегрируя выражение в пределах расстояния между двумя
Δqi+1 – Δqi = ψ2 – ψ1
или разность значений функции тока, cоот-ветствующих двум линиям тока, равняется расходу струи, ограниченной этими двумя линиями токa.
Плоскопараллельное движение жидкости
Слайд 20Потенциал скорости и функция тока взаимоза-висимы.
Например,
откуда
Плоскопараллельное движение жидкости
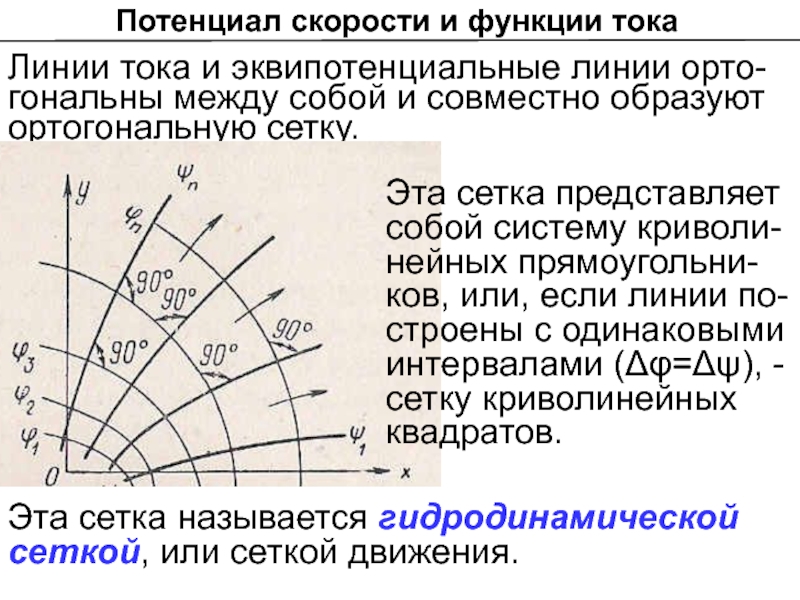
Слайд 21Потенциал скорости и функции тока
Линии тока и эквипотенциальные линии орто-гональны между
Эта сетка представляет собой систему криволи-
нейных прямоугольни-
ков, или, если линии по-
строены с одинаковыми интервалами (Δφ=Δψ), - сетку криволинейных квадратов.
Эта сетка называется гидродинамической сеткой, или сеткой движения.
Слайд 22Гидродинамическая сетка имеет большое практическое значение; если она построена, то задача
стью решена.
Плоскопараллельное движение жидкости
Сетку можно строить приближенно, не зная алгебраического выражения функций φ и ψ , а зная только границы потока, т. е. расположе-
ние жестких неподвижных стенок, в которых движется поток.
Слайд 23Эти стенки являются крайними линиями тока, между ними располагают промежуточные линии
Перпендикулярно им располагают эквипотен-циали, так чтобы сетка состояла из криволи-нейных квадратов.
Плоскопараллельное движение жидкости
Если средние линии в каждом квaдpaте равны, то построение выполнено правильно. Так, средняя линия а-а должна быть равна по длине линии δ- δ.
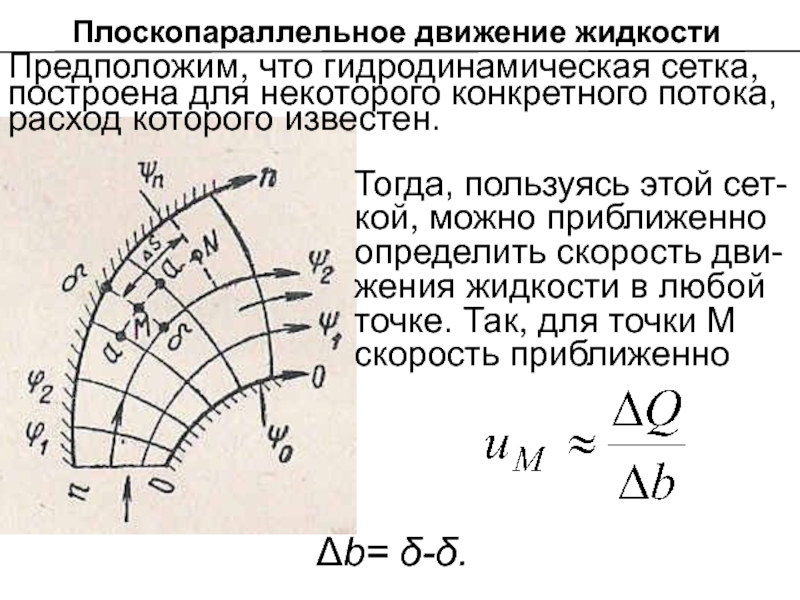
Слайд 24Тогда, пользуясь этой сет-кой, можно приближенно определить скорость дви-жения жидкости в
Δb= δ-δ.
Плоскопараллельное движение жидкости
Предположим, что гидродинамическая сетка, построена для некоторого конкретного потока, расход которого известен.