- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Система сил, моменты. Геометрический метод сложения сил, приложенных в одной точке презентация
Содержание
- 1. Система сил, моменты. Геометрический метод сложения сил, приложенных в одной точке
- 2. Геометрический метод сложения сил, приложенных в одной
- 4. По правилу треугольника сложим последовательно данные силы.
- 5. Фигура ОАВСD называется силовым многоугольником. Замыкающая
- 6. Проекция силы на ось. Проекция вектора
- 7. Проекция силы на ось координат равна произведению
- 8. Fx = Fcos α = Fcos180°
- 9. Из ΔОАВ: Fx=F cos α, Fx=F sin
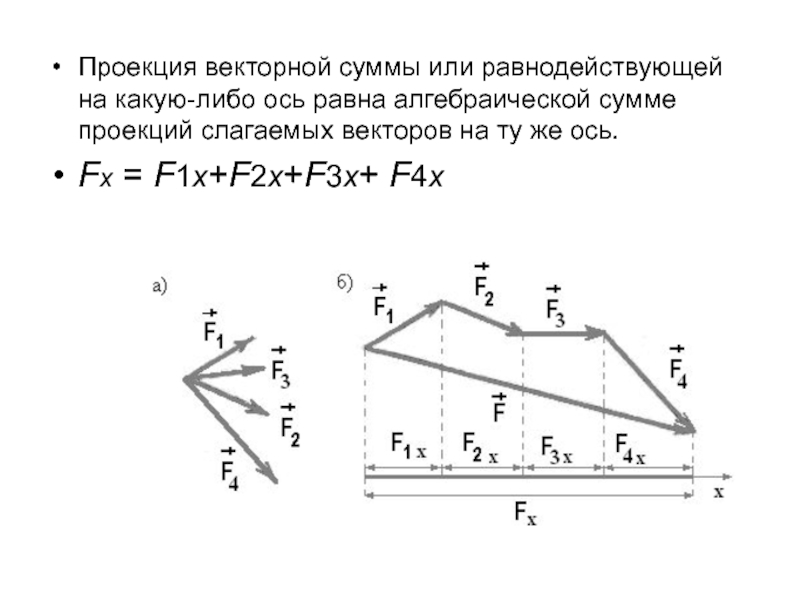
- 10. Проекция векторной суммы или равнодействующей на какую-либо
- 11. Пара сил и моменты сил Две
- 12. Действие пары сил на твердое тело состоит
- 13. Эффект действия пары сил полностью определяется ее
- 14. Момент пары сил будем считать положительным, если
- 15. Две пары сил считаются эквивалентными в том
- 16. Момент силы относительно точки и оси
- 17. Момент силы F относительно определяется произведением силы
- 18. Для определения момента силы относительно оси нужно
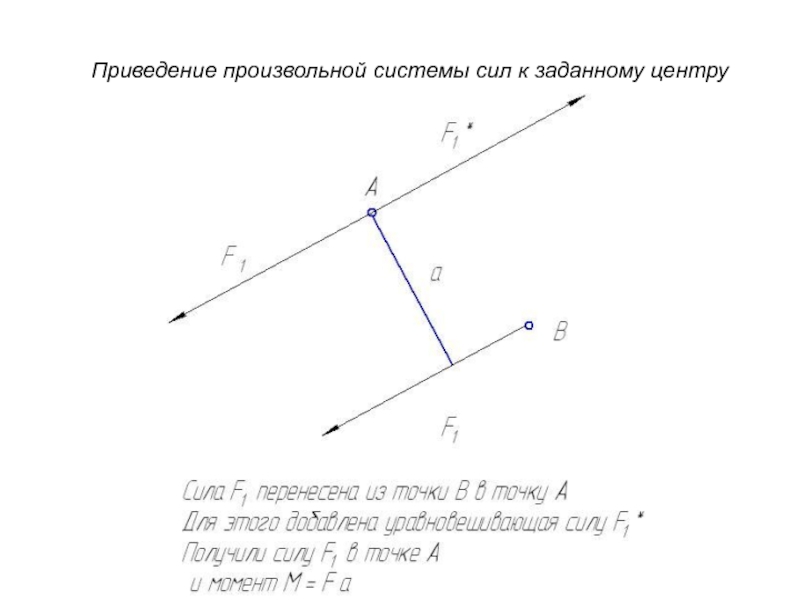
- 19. Приведение произвольной системы сил к заданному центру
- 20. Приведем систему трех произвольно расположенных сил F1,
- 21. Произвольно расположенные в пространстве силы, можно привести
- 22. Для вычисления главного вектора R* системы сил,
- 23. Все присоединенные пары сил лежат в одной
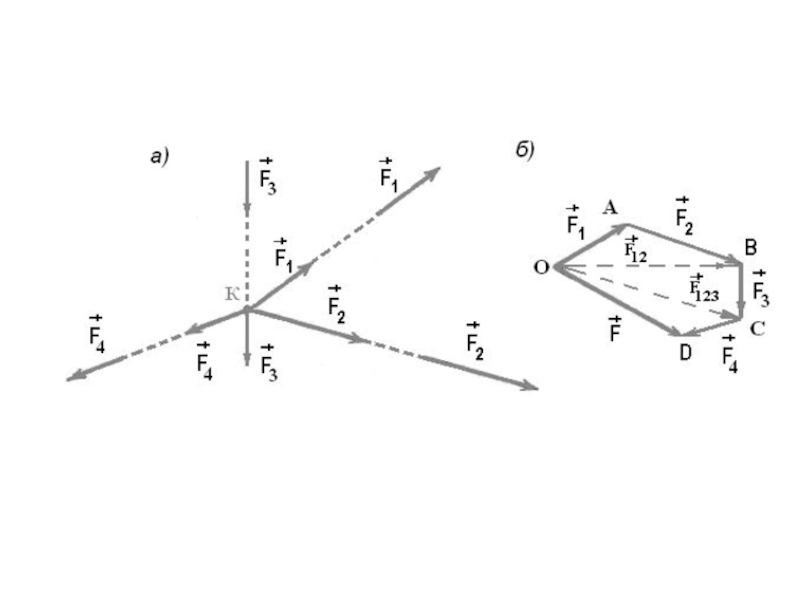
Слайд 2Геометрический метод сложения сил, приложенных в одной точке
Поскольку силу можно
переносить по линии ее действия, то сходящиеся силы всегда можно перенести в одну точку – в точку пересечения этих линий действия. Пусть даны четыре силы. Перенесем эти силы в точку К.
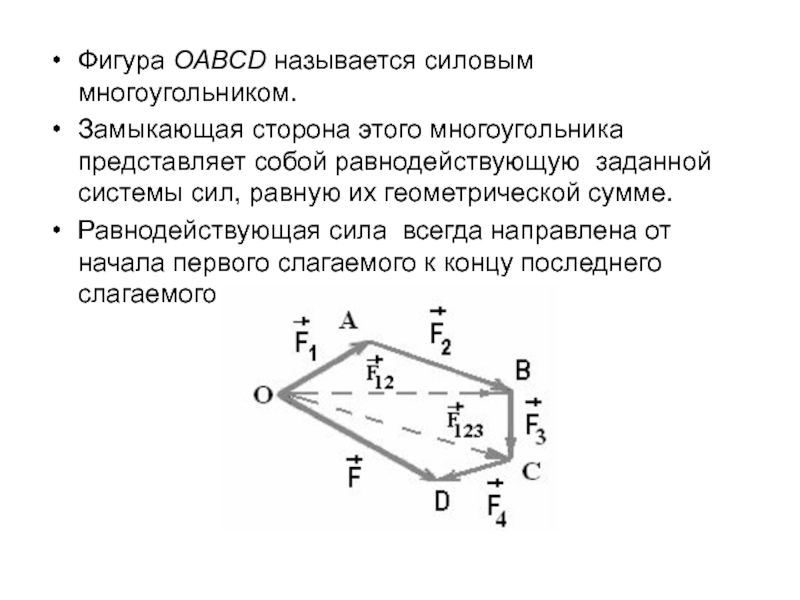
Слайд 5Фигура ОАВСD называется силовым многоугольником.
Замыкающая сторона этого многоугольника представляет собой
равнодействующую заданной системы сил, равную их геометрической сумме.
Равнодействующая сила всегда направлена от начала первого слагаемого к концу последнего слагаемого
Равнодействующая сила всегда направлена от начала первого слагаемого к концу последнего слагаемого
Слайд 6Проекция силы на ось.
Проекция вектора на ось является скалярной величиной,
которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.
Проекция вектора считается положительной, если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной, если направление от начала проекции к ее концу противоположно положительному направлению оси.
Проекция вектора считается положительной, если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной, если направление от начала проекции к ее концу противоположно положительному направлению оси.
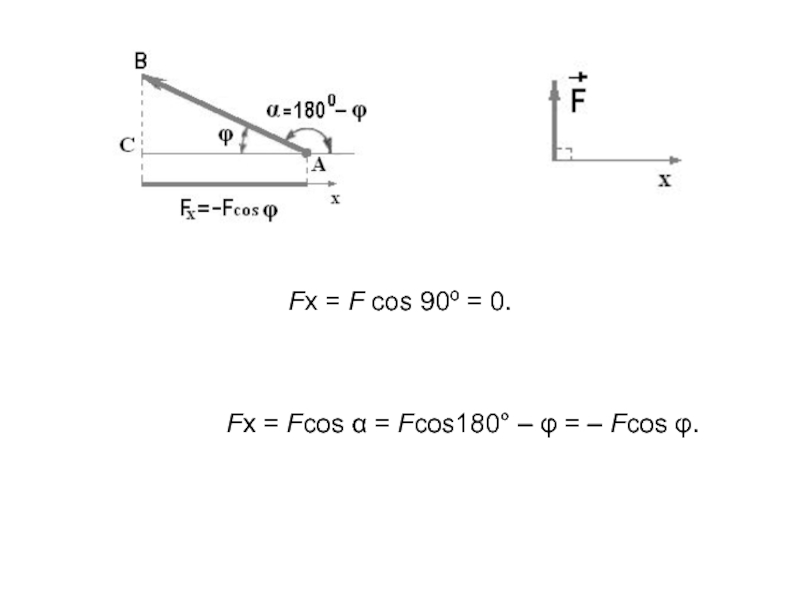
Слайд 7Проекция силы на ось координат равна произведению модуля силы на косинус
угла между вектором силы и положительным направлением оси.
Fx = F cos α
Fx = F cos α
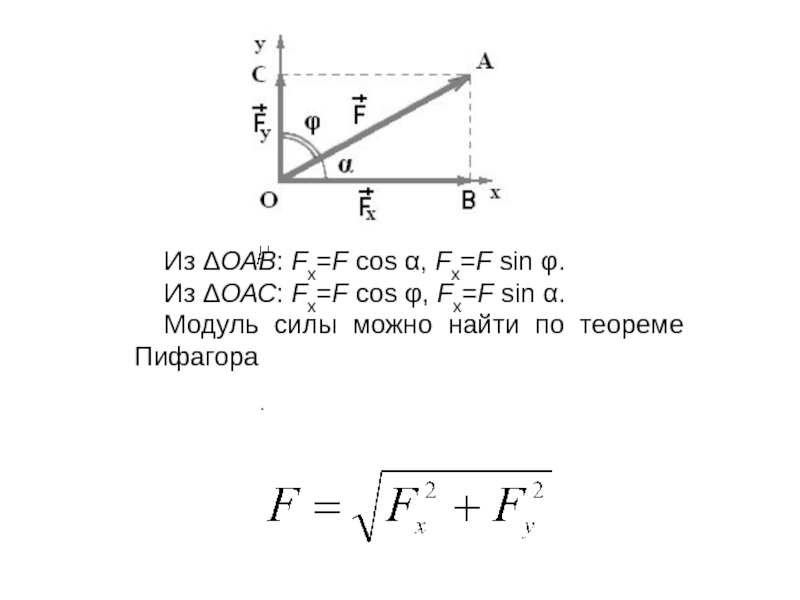
Слайд 9Из ΔОАВ: Fx=F cos α, Fx=F sin φ.
Из ΔОАС: Fx=F cos
φ, Fx=F sin α.
Модуль силы можно найти по теореме Пифагора
Модуль силы можно найти по теореме Пифагора
.
Слайд 10Проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме
проекций слагаемых векторов на ту же ось.
Fх = F1x+F2x+F3x+ F4x
Fх = F1x+F2x+F3x+ F4x
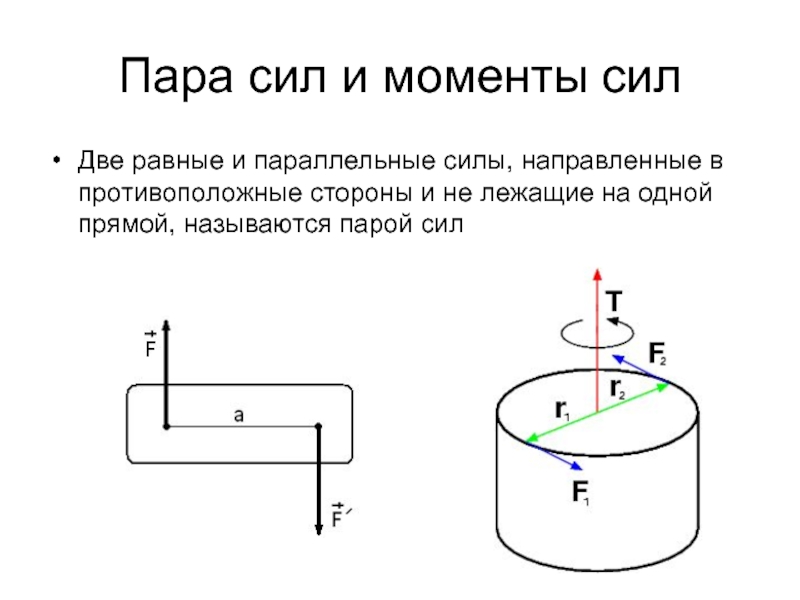
Слайд 11Пара сил и моменты сил
Две равные и параллельные силы, направленные
в противоположные стороны и не лежащие на одной прямой, называются парой сил
Слайд 12Действие пары сил на твердое тело состоит в том, что она
стремится вращать это тело.
Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил.
М = F·a = F '·а.
Кратчайшее расстояние между линиями действия сил а называется плечом пары.
Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил.
М = F·a = F '·а.
Кратчайшее расстояние между линиями действия сил а называется плечом пары.
Слайд 13Эффект действия пары сил полностью определяется ее моментом.
Момент пары в
СИ измеряется в ньютон-метрах (Н·м) или в единицах, кратных ньютон-метру: кН·м, МН·м
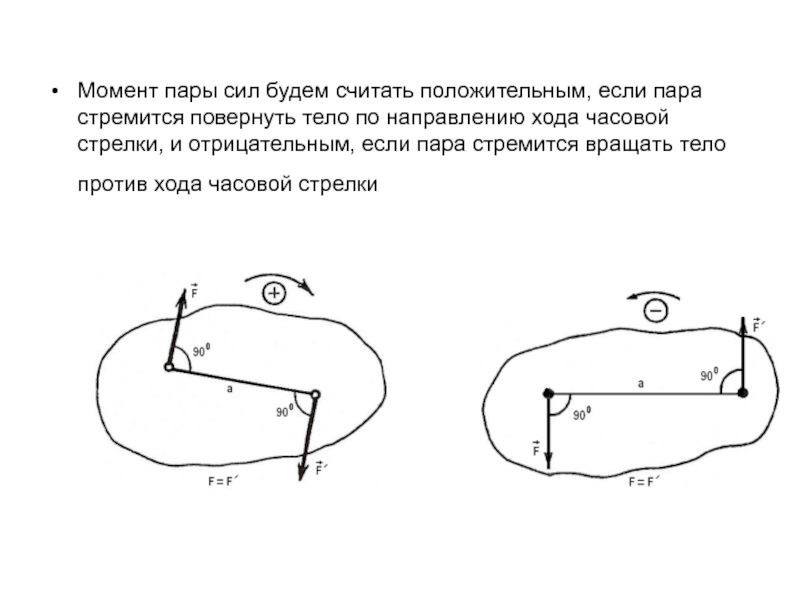
Слайд 14Момент пары сил будем считать положительным, если пара стремится повернуть тело
по направлению хода часовой стрелки, и отрицательным, если пара стремится вращать тело против хода часовой стрелки
Слайд 15Две пары сил считаются эквивалентными в том случае, если после замены
одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие.
Сложение пар производится алгебраическим суммированием их моментов, т. е. момент результирующей пары равен алгебраической сумме моментов составляющих пар.
М = М1 + М2 + … + Мn =
Сложение пар производится алгебраическим суммированием их моментов, т. е. момент результирующей пары равен алгебраической сумме моментов составляющих пар.
М = М1 + М2 + … + Мn =
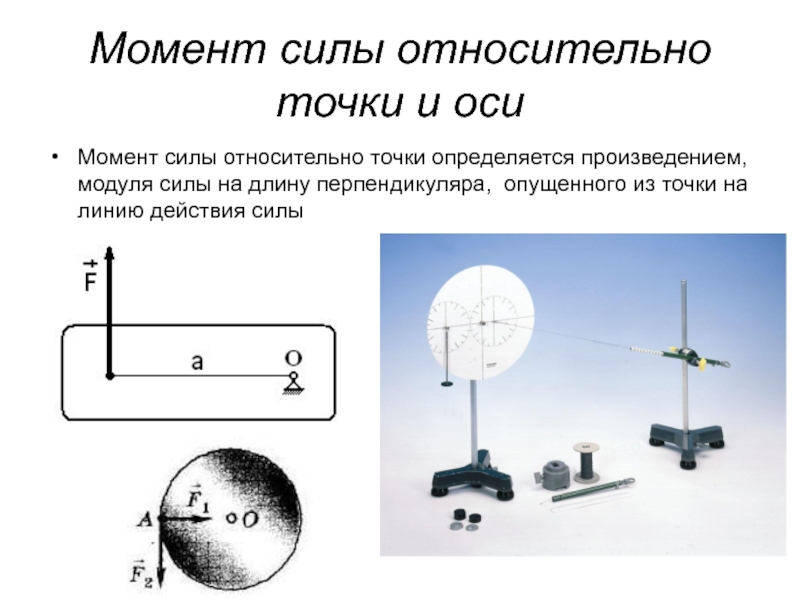
Слайд 16Момент силы относительно точки и оси
Момент силы относительно точки определяется
произведением, модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы
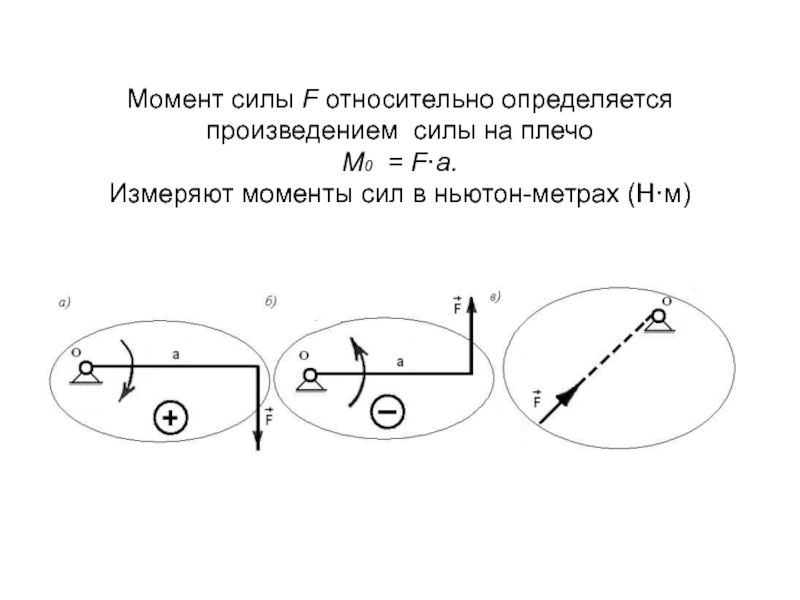
Слайд 17Момент силы F относительно определяется произведением силы на плечо М0 =
F·a.
Измеряют моменты сил в ньютон-метрах (Н·м)
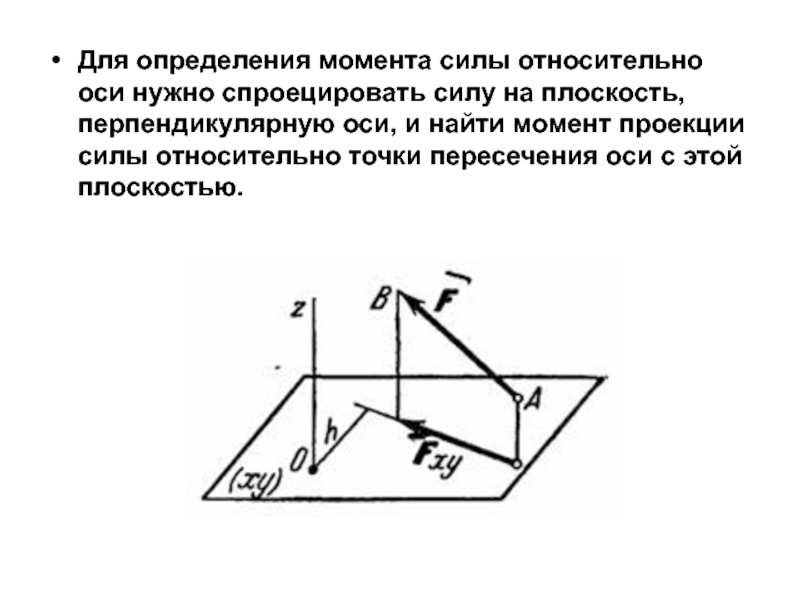
Слайд 18Для определения момента силы относительно оси нужно спроецировать силу на плоскость,
перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью.
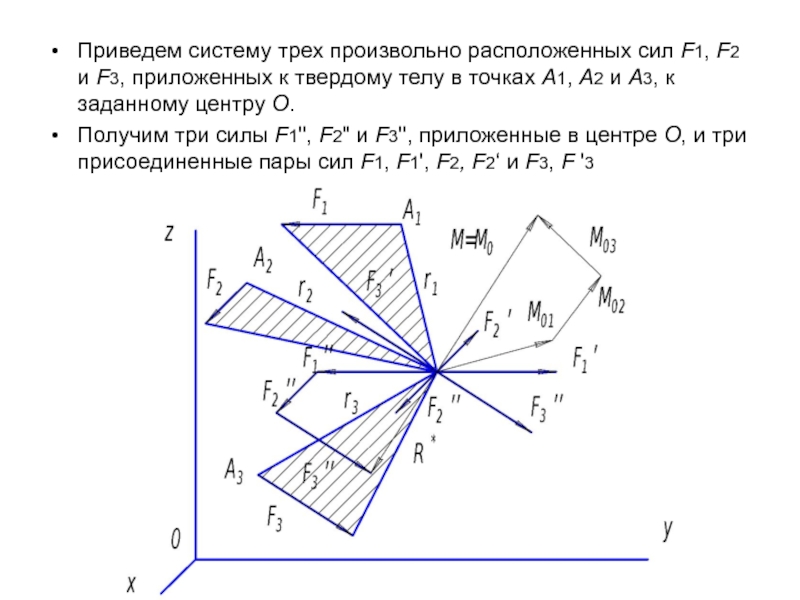
Слайд 20Приведем систему трех произвольно расположенных сил F1, F2 и F3, приложенных
к твердому телу в точках А1, А2 и А3, к заданному центру О.
Получим три силы F1'', F2" и F3'', приложенные в центре О, и три присоединенные пары сил F1, F1', F2, F2‘ и F3, F '3
Получим три силы F1'', F2" и F3'', приложенные в центре О, и три присоединенные пары сил F1, F1', F2, F2‘ и F3, F '3
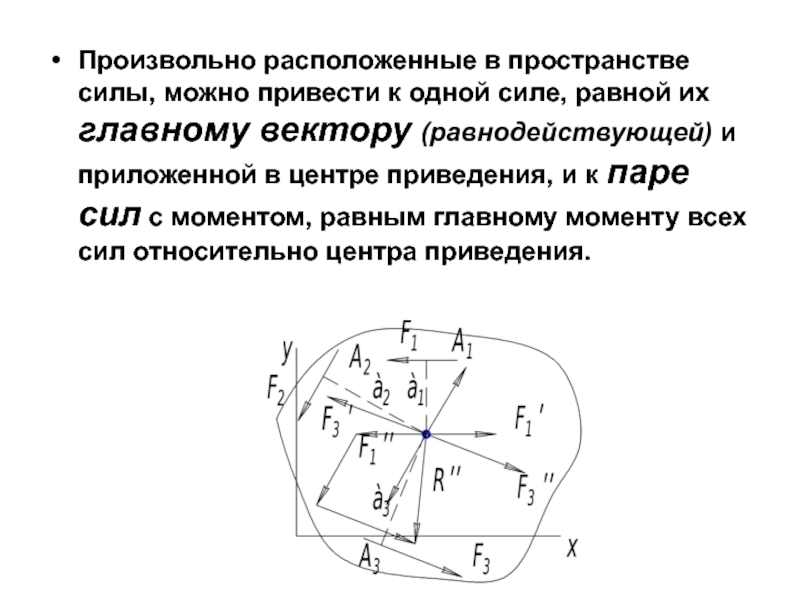
Слайд 21Произвольно расположенные в пространстве силы, можно привести к одной силе, равной
их главному вектору (равнодействующей) и приложенной в центре приведения, и к паре сил с моментом, равным главному моменту всех сил относительно центра приведения.
Слайд 22Для вычисления главного вектора R* системы сил, произвольно расположенных на плоскости, воспользуемся
методом проекций.
R*=F1+F2+…+Fn.
Обозначив Rx, Ry – проекции главного вектора на оси координат, получим
Rx = F1x+F2x+…+Fnx,
Ry = F1y+F2y+…+Fny,
где F1x, F2x, ..., Fnx; F1y, F2y, Fny – проекции сил F1, F2, …, Fn соответственно на оси x и y.
Модуль и направление главного вектора R* определяются по формулам
.
Обозначив Rx, Ry – проекции главного вектора на оси координат, получим
Rx = F1x+F2x+…+Fnx,
Ry = F1y+F2y+…+Fny,
где F1x, F2x, ..., Fnx; F1y, F2y, Fny – проекции сил F1, F2, …, Fn соответственно на оси x и y.
Модуль и направление главного вектора R* определяются по формулам
.
Слайд 23Все присоединенные пары сил лежат в одной плоскости.
Момент эквивалентной им
пары сил, равный главному моменту системы сил относительно центра приведения, определяется согласно как алгебраическая сумма моментов сил относительно этого центра.
М = М0 =.
М = М0 =.