ядра дислокаций. Барьер
Пайерлса. Механизмы пластической
деформации.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сдвиговая прочность кристаллов. Модели ядра дислокаций. Барьер Пайерлса. Механизмы пластической деформации презентация
Содержание
- 1. Сдвиговая прочность кристаллов. Модели ядра дислокаций. Барьер Пайерлса. Механизмы пластической деформации
- 2. Прочность кристаллов на сдвиг
- 3. Атомная структура ядра дислокации Fe, Cu –
- 4. Пластическая деформация кристаллов A x Для малых
- 5. Модель Френкеля σ ≡ τ = -dU/dx
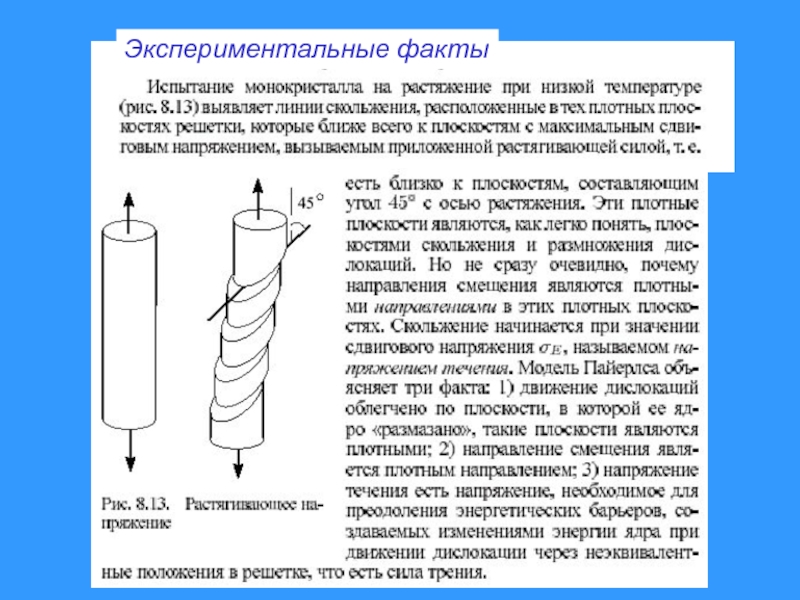
- 8. Экспериментальные факты
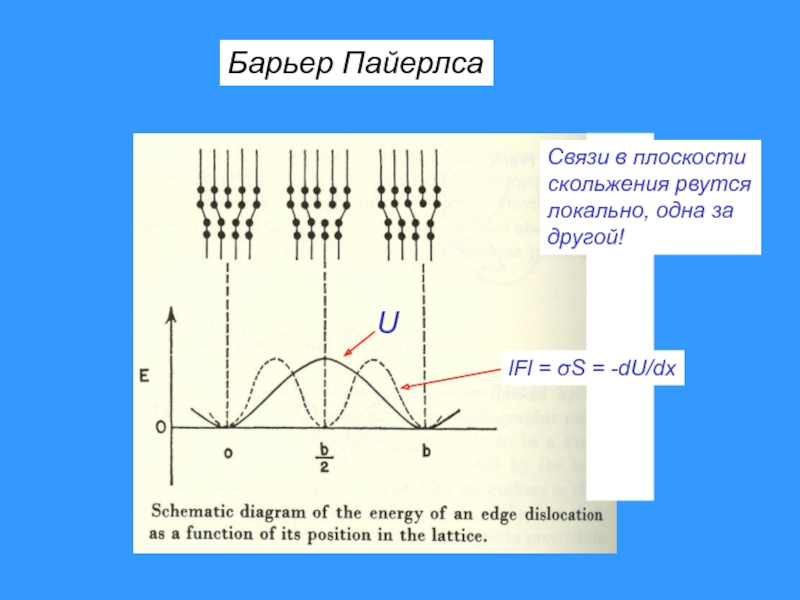
- 9. Барьер Пайерлса Связи в плоскости скольжения
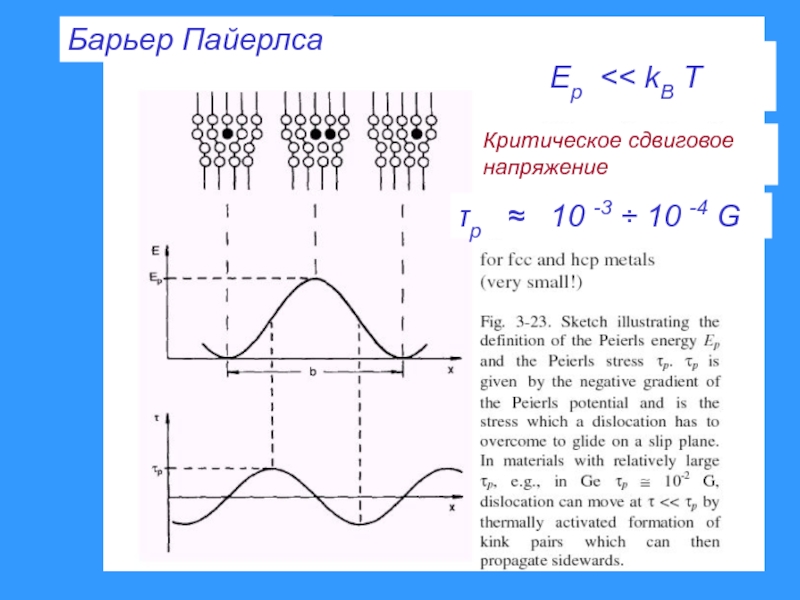
- 10. Барьер Пайерлса τp ≈ 10 -3 ÷ 10 -4 G Ep
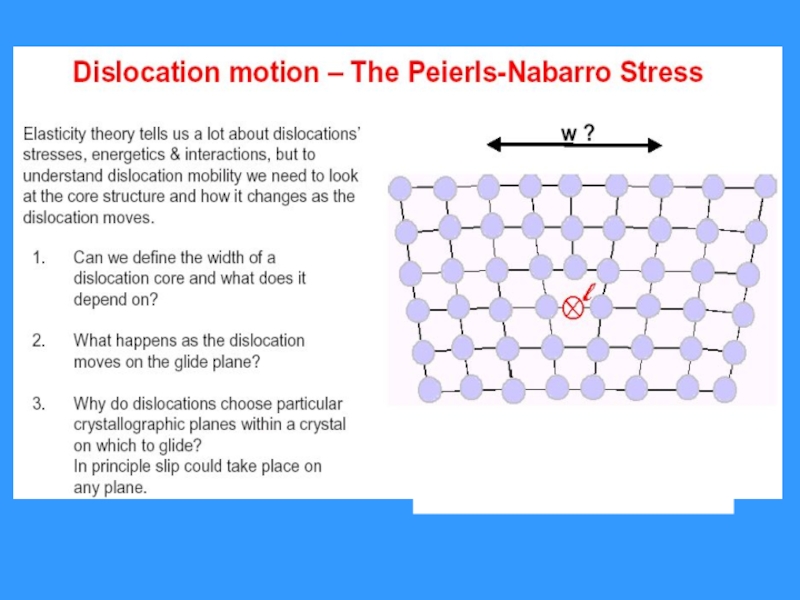
- 11. Модель Пайерлса - Набарро «ширина» ядра дислокации
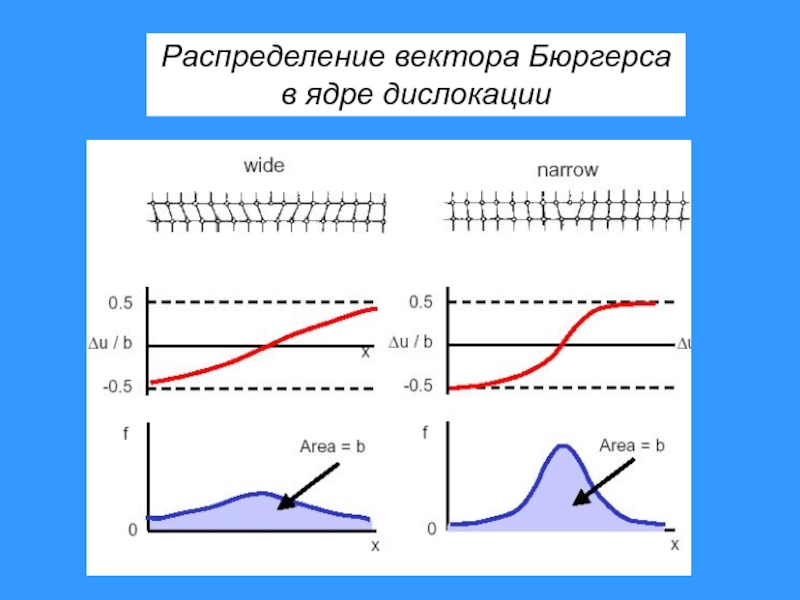
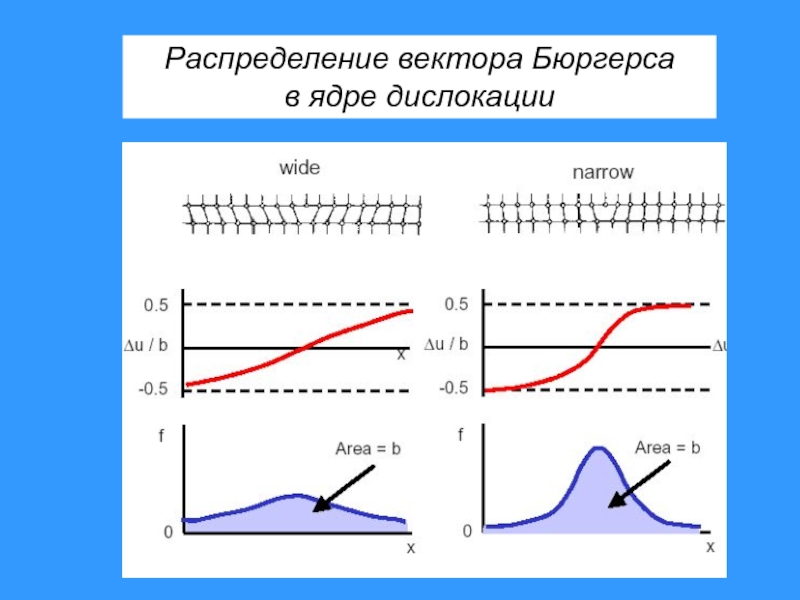
- 12. Распределение вектора Бюргерса в ядре дислокации
- 15. Чтобы получить кон-
- 16. Сдвиг одной половины кристалла относительно другой на
- 17. Функция взаимного смещения двух атомов, расположенных
- 18. σ = Расположение n одноименных дислокаций
- 19. Распределение вектора Бюргерса в ядре дислокации
- 20. A x Для малых сдвиговых деформаций, ε
- 23. - определяет «ширину» ядра дислокации
- 25. Пайерловский рельеф кристалла
- 26. ζ = d/2(1 - ν) ≈ (3/4)d;
- 27. ГЦК структура Коэффициент упаковки
- 28. τp ≈ 10
- 29. Оценки упругой энергии дислокации При обычных значениях
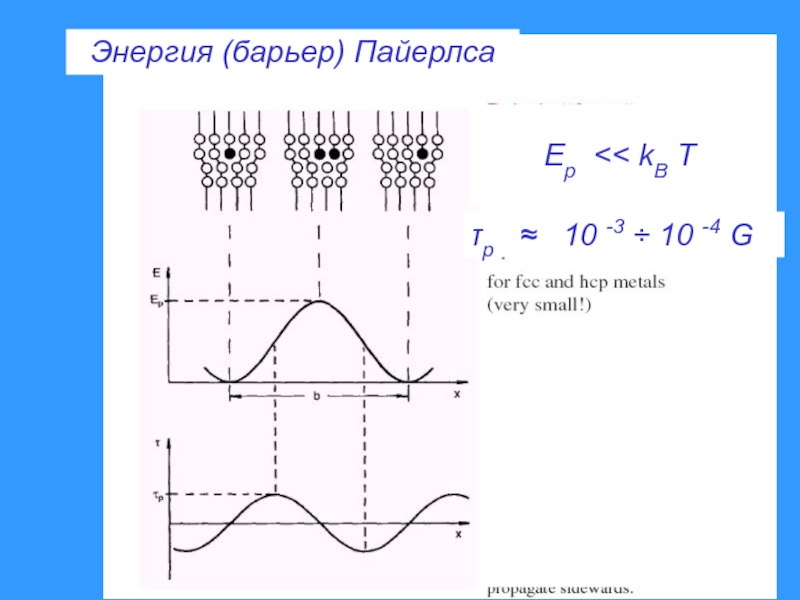
- 30. τp ≈ 10 -3 ÷ 10 -4 G Энергия (барьер) Пайерлса Ep
- 31. Пластическая деформация - движение и размножение
- 32. Дислокации в гранецентрированной кубической решетке Дислокационные сетки с тройными узлами
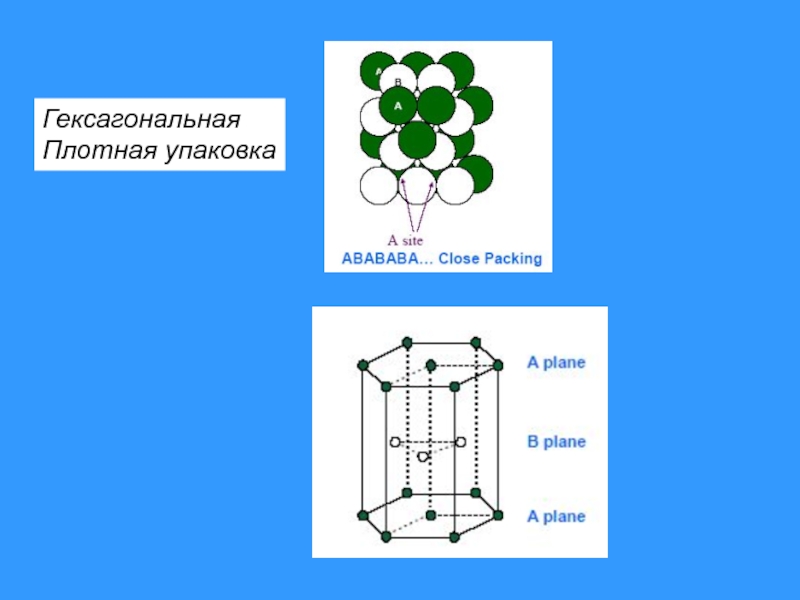
- 34. Гексагональная Плотная упаковка
- 36. Common crystal
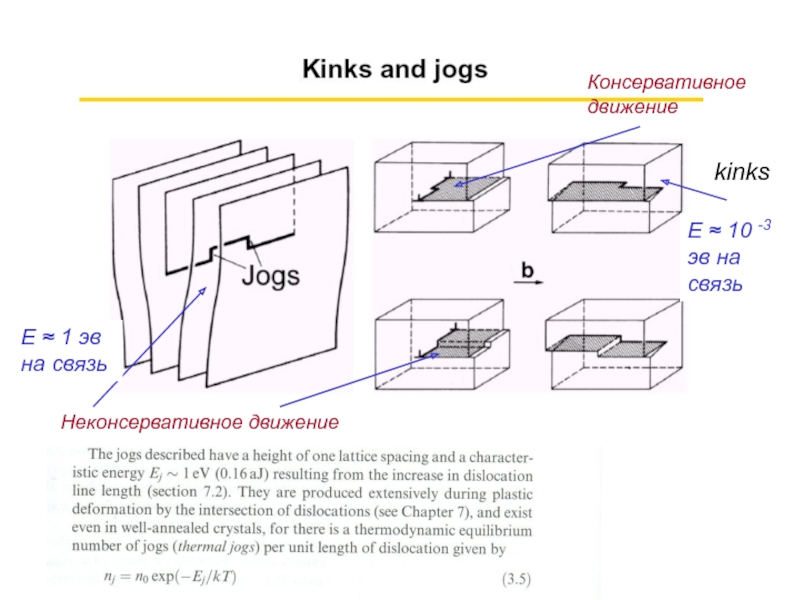
- 37. kinks Консервативное движение Неконсервативное движение Е ≈
- 38. Дефекты дислокационной линии в плоскости скольжения
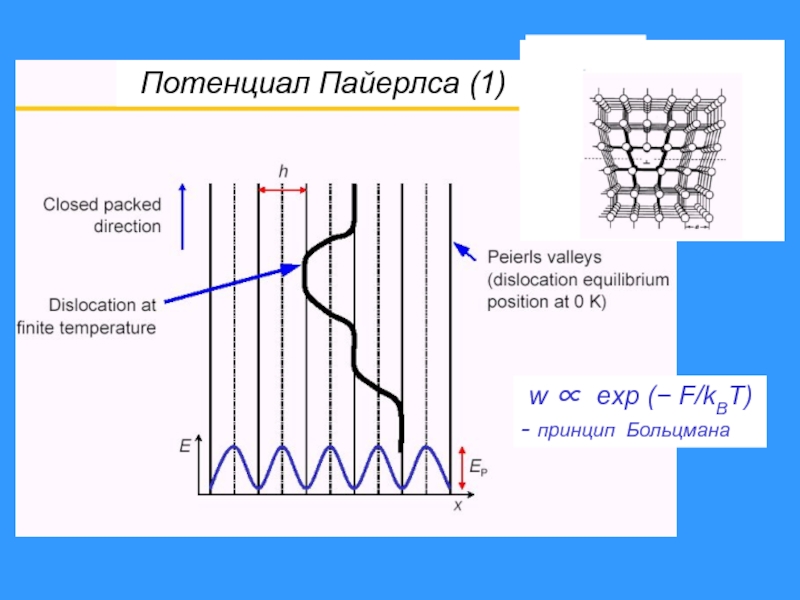
- 39. Потенциал Пайерлса (1) w ∝ exp (− F/kBT) - принцип Больцмана
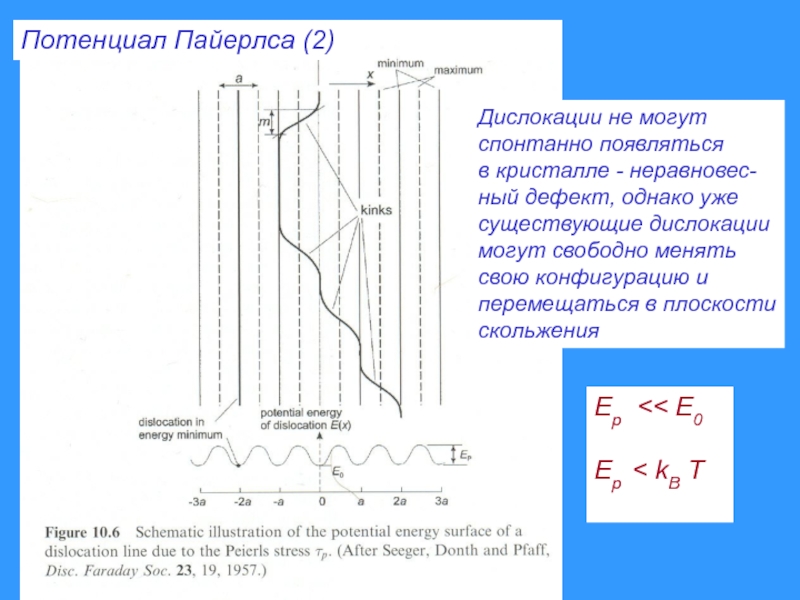
- 41. Потенциал Пайерлса (2) Ep
- 42. Необходимо отметить, что величины энергии Пайерлса Ep
Прочность кристаллов на сдвиг
Слайд 1Профессор Б.И.Островский
Физика реального кристалла
ostr@cea.ru
Сдвиговая прочность кристаллов.
Модели
Слайд 3Атомная структура ядра дислокации
Fe, Cu – пластичны; Si, Ge –
хрупки
??
Пластичные
материалы
можно ковать!
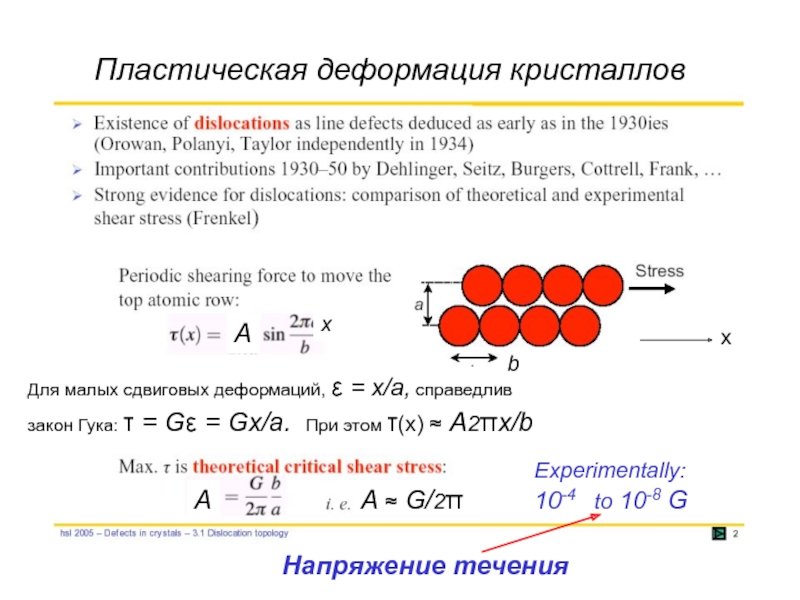
Слайд 4Пластическая деформация кристаллов
A
x
Для малых сдвиговых деформаций, ε = x/a, справедлив
закон
Гука: τ = Gε = Gx/a. При этом τ(x) ≈ A2πx/b
A
A ≈ G/2π
x
b
Experimentally:
10-4 to 10-8 G
Напряжение течения
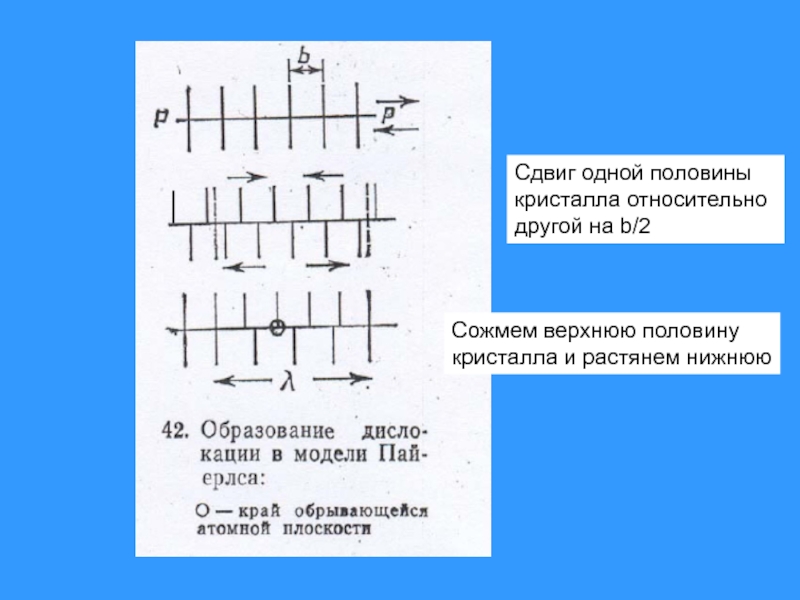
Слайд 16Сдвиг одной половины кристалла относительно
другой на b/2
Сожмем верхнюю половину
кристалла и
растянем нижнюю
Слайд 17
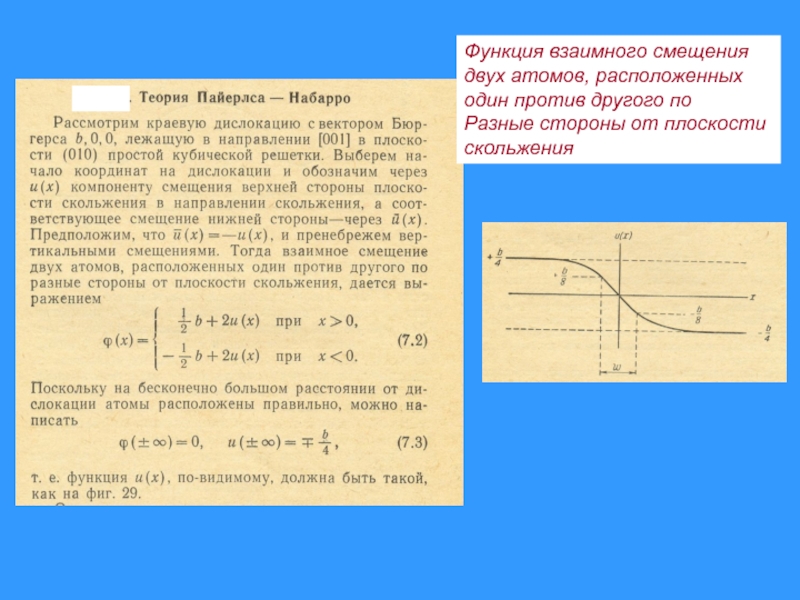
Функция взаимного смещения
двух атомов, расположенных
один против другого по
Разные стороны от
плоскости
скольжения
скольжения
Слайд 20A
x
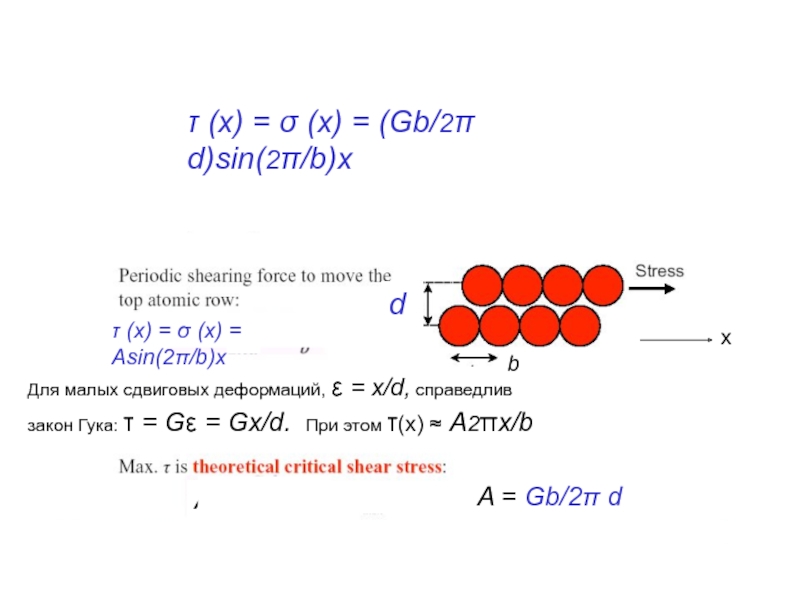
Для малых сдвиговых деформаций, ε = x/d, справедлив
закон Гука: τ
= Gε = Gx/d. При этом τ(x) ≈ A2πx/b
A
x
b
τ (x) = σ (x) = (Gb/2π d)sin(2π/b)x
d
τ (x) = σ (x) = Asin(2π/b)x
A = Gb/2π d
Слайд 23- определяет «ширину»
ядра дислокации
2ζ
для сдвиговых напряжений, полученных на основе
континуального подхода Вольтерра
b/4
- b/4
D = Gb/2π(1-ν);
Слайд 26ζ = d/2(1 - ν) ≈ (3/4)d;
exp(-3π d/b)
≈ 2x10 -4 (ГЦК решетка)
20.32
d/b =
b)
≈ 1/3 –
Коэффициент
Пуассона
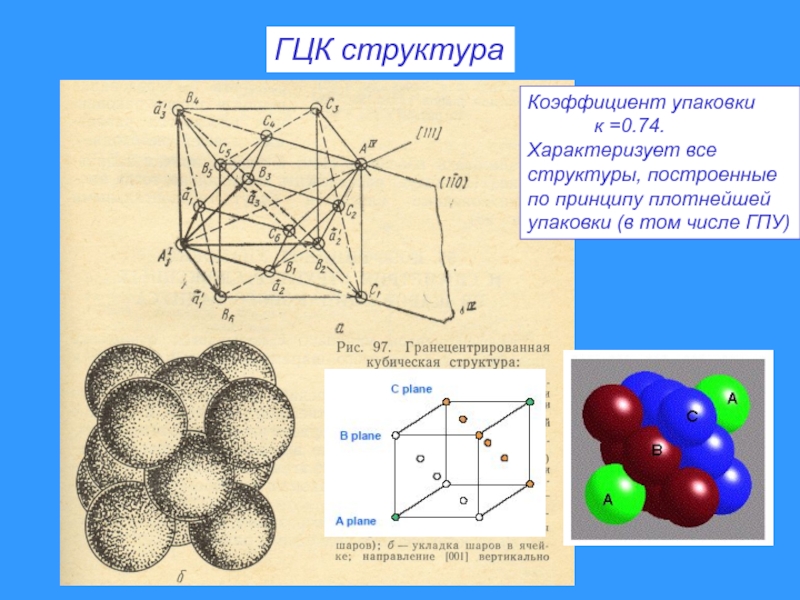
Слайд 27ГЦК структура
Коэффициент упаковки
к =0.74.
Характеризует
все
структуры, построенные
по принципу плотнейшей
упаковки (в том числе ГПУ)
структуры, построенные
по принципу плотнейшей
упаковки (в том числе ГПУ)
Слайд 28
τp ≈ 10 -4 G (ГЦК решетка)
Ep =
τp b2/2 π ≈ 10 -4 Gb2
Что в пересчете на одну связь дает:
Epbond ≈ 5 x 10 -4 эв
Что в пересчете на одну связь дает:
Epbond ≈ 5 x 10 -4 эв
Для сравнения: kB T = 1.4 10-16 эрг/К x 300 К ≈ 4x 10-14 эрг
≈ 3x10-2 эв
Слайд 29Оценки упругой энергии дислокации
При обычных значениях плотности дислокаций ρ =107 см-2,
среднее
расстояние между ними составляет R ≈ ρ-1/2 ≈ 3.10-4 см, что дает
для
расстояние между ними составляет R ≈ ρ-1/2 ≈ 3.10-4 см, что дает
для
≈ 10
и
полн
/L =
≈
При G ≈ 1012 дин.см-2 и b = 2.10 -8 см имеем:
полн
/L =
≈
4.10 -4 эрг/см
Что в пересчете на одну связь дает:
Ebond = 4.10 -4 эрг/см x 2.10 -8 см = 8.10-12 эрг 5 эв
≈
≈
Слайд 31Пластическая деформация - движение и размножение
дислокаций в плоскости скольжения
τp ≈
exp(-kd/a)
a - min
Summary
Слайд 36 Common crystal structures in metals:
Face centered
cubic (fcc): ABCABC… packing: Ni, Cu, Ag, Al, Au
Hexagonal close packed (hcp): ABABAB … packing: Mg, Zn, Co, Ti
Hexagonal close packed (hcp): ABABAB … packing: Mg, Zn, Co, Ti
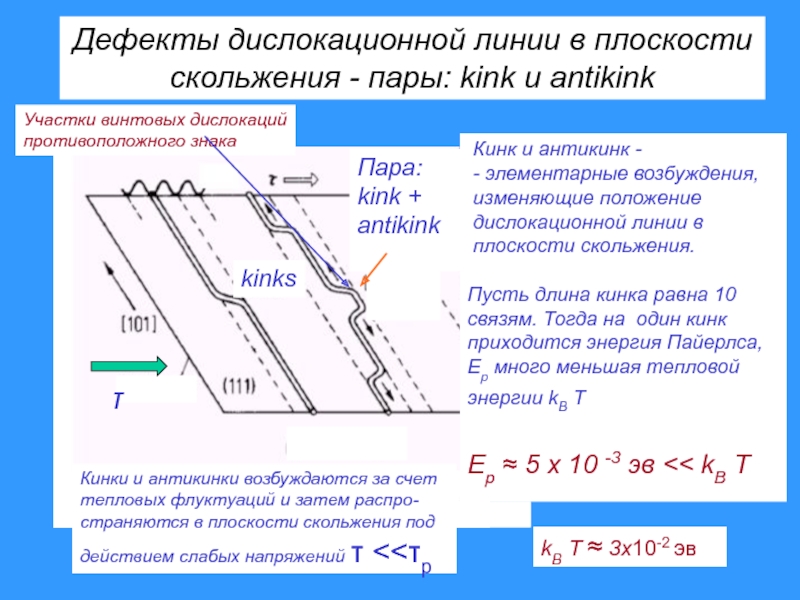
Слайд 38Дефекты дислокационной линии в плоскости
скольжения - пары: kink и antikink
Кинк и антикинк -
- элементарные возбуждения,
изменяющие положение
дислокационной линии в
плоскости скольжения.
Пусть длина кинка равна 10
связям. Тогда на один кинк
приходится энергия Пайерлса,
Ep много меньшая тепловой
энергии kB T
Ep ≈ 5 x 10 -3 эв << kB T
Кинки и антикинки возбуждаются за счет
тепловых флуктуаций и затем распро-
страняются в плоскости скольжения под
действием слабых напряжений τ <<τp
kinks
Пара:
kink +
antikink
kB T ≈ 3x10-2 эв
τ
Участки винтовых дислокаций
противоположного знака
Слайд 41Потенциал Пайерлса (2)
Ep
появляться
в кристалле - неравновес-
ный дефект, однако уже
существующие дислокации
могут свободно менять
свою конфигурацию и
перемещаться в плоскости
скольжения
в кристалле - неравновес-
ный дефект, однако уже
существующие дислокации
могут свободно менять
свою конфигурацию и
перемещаться в плоскости
скольжения
Слайд 42Необходимо отметить, что величины энергии Пайерлса Ep и
критического напряжения сдвига
τp чрезвычайно чувствительны
к природе межатомных сил и характеру упаковки атомов в
элементарной ячейке.
τp ≈ 10 -4 ÷ 10 -5 G для ГЦК и ГПУ металлов;
τp ≈ 10 -2 для ковалентных кристаллов типа
кремния и алмаза
к природе межатомных сил и характеру упаковки атомов в
элементарной ячейке.
τp ≈ 10 -4 ÷ 10 -5 G для ГЦК и ГПУ металлов;
τp ≈ 10 -2 для ковалентных кристаллов типа
кремния и алмаза
Заключительные замечания
